定积分计算的解题技巧

■江苏省张家港职业教育中心校 韩文美

定积分计算的解题技巧

■江苏省张家港职业教育中心校 韩文美

定积分的计算是高考中一个基本考点,常见的计算方法有定义法、几何意义法与微积分基本公式法等。高中阶段,由于定义法求定积分(四个基本步骤:分割、近似代替、求和、取极限)过程比较烦琐,实际计算中不太实用。在实际应用中,一般利用几何意义法、微积分基本公式法、定积分性质法以及被积函数奇偶性法等来计算求解。

1.几何意义法

根据定积分的几何意义,对于在区间[a,b]上函数f(x)连续且恒有f(x)≥0,那么定积分表示由直线x=a,x=b(a≠b), y=0和曲线y=f(x)所围成的曲边梯形的面积。特别地,对于一些特殊函数的定积分求解,可以借助特殊图形(如:圆等)加以计算。在实际求解曲边梯形的面积时要注意在x轴上方的面积取正号,在x轴下方的面积取负号。

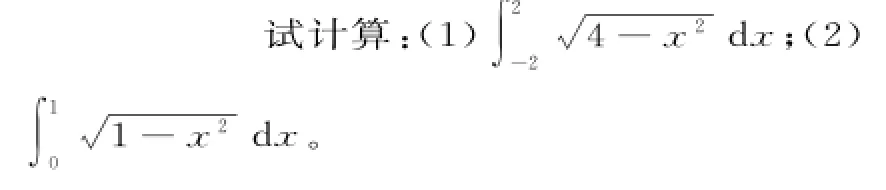
分析：结合题中被积函数所表示的曲线为相应的圆的一部分,利用定积分的几何意义,结合圆的面积公式来计算。

由定积分的几何意义可知,此积分计算的是半圆的面积。

(2)被积函数y=1-x2(x∈[0,1])表示的曲线是圆心在原点,半径为1的四分之一圆周。

由定积分的几何意义可知,此积分计算的是四分之一圆的面积。

点评:本题主要考查定积分的计算,圆的面积公式。利用定积分的几何意义计算定积分时,关键是正确判断被积函数所表示的曲线以及变量的取值限制,把问题转化为求相对应的图形的面积。

2.微积分基本公式法

微积分基本公式揭示了定积分与不定积分的内在联系,为计算定积分提供了一种十分简捷的方法。如果f(x)是区间[a,b]上的连续函数,并且F'(x)=f(x),则∫baf(x)dx =F(b)-F(a)。其步骤为:第一步:求f(x)的一个原函数F(x);第二步:计算F(b)-F(a)的值。

分析：直接根据微积分基本公式进行求解即可。

故答案为0。

点评:本题主要考查定积分的计算与函数值的计算问题。利用微积分的基本公式计算定积分时应注意两点:一是正确选择被积函数,二是注意被积区间,其结果是原函数在[a,b]上的改变量F(b)-F(a)。

3.定积分性质法

如果直接利用定积分的定义求解定积分难度比较大,而利用微积分基本定理的相应公式计算时计算量有点大,可以考虑利用定积分的相应性质加以转化与计算。

分析：通过定积分的相关性质,将被积函数转化为x2,直接利用已知条件,大大简化计算过程,也体现了发散思维能力的训练。

点评:本题主要考查定积分的计算,定积分的相关性质。结合已知条件,若直接利用定积分的定义求相应的定积分的值难度非常大,而通过逆用定积分的相应性质加以分析求解,就非常巧妙简捷。

4.被积函数奇偶性法

如果被积函数是奇函数,则其在对称区间上的定积分为0;如果被积函数是偶函数,则其在对称区间上的定积分等于正数区间的2倍。利用被积函数奇偶性法,可以使得一些定积分的计算化难为易,简单快捷。

(2014年湖北省理科卷第6题)若函数f(x),g(x)满足0,则称f(x),g(x)为区间[-1,1]上的一组正交函数。给出三组函数:

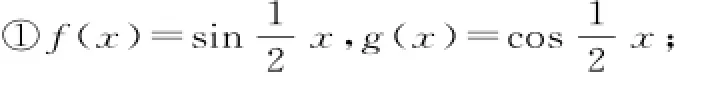
②f(x)=x+1,g(x)=x-1;

③f(x)=x,g(x)=x2。

其中为区间[-1,1]上的正交函数的组数是( )

A.0 B.1 C.2 D.3

分析：常规方法可根据创新定义分别计算各组函数对应的定积分的值,结合题目条件加以判断。而直接利用创新定义,若函数f(x),g(x)满足∫1-1f(x)g(x)dx=0,则对应的函数f(x)g(x)必须为奇函数,这样判断更为直观。

解：由题意知,要满足f(x),g(x)是区间[-1,1]上的正交函数,需满足∫1-1f(x)·

g(x)dx=0,此时f(x)g(x)必须是奇函数。

②中,f(x)g(x)=(x+1)(x-1)= x2-1是偶函数,不满足条件;

③中,f(x)g(x)=x·x2=x3是奇函数,满足条件。

综上,在区间[-1,1]上是正交函数的组数是2,故答案为C。

点评:本题主要在新定义下考查定积分的计算,函数的基本性质。采用以上的被积函数奇偶性法来处理,显然比直接去计算相应的定积分更为简单快捷,理解起来比较容易,处理起来也比较简单。

在实际的定积分计算中,有时可以单一使用相关的方法,有时要综合以上多种相关的方法加以应用。正确掌握定积分的定义,把握相关的计算方法是解决定积分计算的关键所在,也是考查的重点。

(责任编辑 徐利杰)