复数及推理与证明全国名校测试题

■河南省虞城县高级中学 何海涛

复数及推理与证明全国名校测试题

■河南省虞城县高级中学 何海涛

一、选择题(本大题共12小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合题目要求的)

A.一 B.二 C.三 D.四

3.关于合情推理和演绎推理,下列说法错误的是( )。

A.合情推理包括归纳推理和类比推理

B.合情推理的结论一定为真

C.演绎推理的主要形式是“三段论”

D.演绎推理中当前提为真时,结论必然为真

A.2 B.-2 C.0 D.1

5.已知复数z满足z z1=z1-2z且有z1=-2+i(i为虚数单位),则=( )。

6.用反证法证明命题“四边形的内角中至少有一个不大于90°”时,应假设的内容是( )。

A.四个内角至多有一个大于90°

B.四个内角都不大于90°

C.四个内角都大于90°

D.四个内角至多有两个大于90°

8.下列推理中属于归纳推理且结论正确的是( )

A.设数列{an}的前n项和为Sn,由an= 2n-1,求出S1=12,S2=22,S3=32,…,可推断:Sn=n2

B.由f(x)=xco sx满足f(-x)= -f(x)对∀x∈R都成立,可推断:f(x)= xco sx为奇函数

C.由圆x2+y2=r2的面积S=πr2,推断:椭圆=1(a＞b＞0)的面积S= abπ

D.由(1+1)2＞21,(2+1)2＞22,(3+1)2＞23,…,推断:对一切n∈N+,(n+1)2＞2n

A.0 B.-1 C.1 D.2

10.设集合M={y|y=|s i nx+co sx|, x∈R},并且集合N=,则集合M∩N=( )。

A.(0,1) B.(0,1]

C.[0,1) D.[0,1]

11.已知双曲线的中心在坐标原点,F为左焦点,A为实轴右顶点,B为虚轴上顶点,当 ,此类双曲线被称为“黄金双曲线”。类比“黄金双曲线”可推算出“黄金椭圆”的离心率为( )。

12.一个同学看到一组数据如下:

1212221222221222222212222222221

……。如果以此规律继续下去,得到一系列的数字,那么在前2017个数字中数字“2”的个数为( )。

A.1970 B.1971C.1972 D.1973二、填空题(本大题共4小题,每小题5分,共20分)

13.若复数z=(x2-3x+2)+(x2-4)i(i为虚数单位,x∈R)是纯虚数,则x=____。

14.已知复数z1=1+i,z2=1-i(i为虚数单位),下面关于复数z1,z2的命题正确的是____。

①p1:z1=z2;②p2:z21=z22;③p3:z1,z2互为共轭复数;④的虚部为i。

16.用数学归纳法证明:1+2+3+…+n3=时,则当n=k+1时,左端应在n=k的基础上加上的项的个数为____个。

三、解答题(本大题共6小题,共70分。解答应写出必要的证明过程或演算步骤)

17.(本小题满分10分)

问实数m为何值时,复平面内表示复数z= m-1+(m2-9)i(i为虚数单位)的点:

(1)位于实轴上;

(2)位于第二或第四象限;

(3)位于抛物线x2=y上。

18.(本小题满分12分)

设复数z=3s i nθ-4co sθi(i为虚数单位)。

(2)若复数z所对应的点在直线x+2y=0上,求s i n 2θ+co s 2θ的值。

19.(本小题满分12分)

20.(本小题满分12分)

21.(本小题满分12分)

设0＜a,b,c＜1,求证:(1-a)b(1-b)c,(1-c)a,不可能同时大于

22.(本小题满分12分)

蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似看成是一个正六边形,图形采用环绕镶嵌模式,其中第一个图有一个蜂巢,第二个图有七个蜂巢,第三个图有十九个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数。

(1)试给出f(6),f(10)的值,并写出f(n)的表达式(不要求证明);

1.B 2.C3.B 4.B 5.B 6.C7.A 8.A 9.C10.C11.B

12.C提示:由这组数据规律发现:

“2”出现的次数为1,3,5,7,…,2n-1;

“1”则在其后每组出现一次。

故1+3+5+…+(2n-1)+n=2017。

则n2+n=2017,44＜n＜45。

则有45个“1”,2017-45=1972(个)“2”。

故选C。

13.x=1

14.③

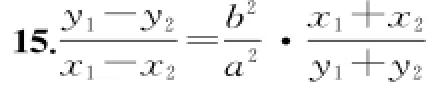
16.3k2+3k+1

17.由题意知复数z的实部为m-1,虚部为m2-9。

(1)当点在实轴上,虚部为0,则m2-9=0,m =±3。

(2)当点位于第二或第四象限时,实虚部异号,则(m-1)(m2-9)＜0,m＜-3或1＜m＜3。

(3)位于抛物线x2=y上时,(m-1)2=m2-9,解得m=5。

18.复数z=3s i nθ-4co sθi。

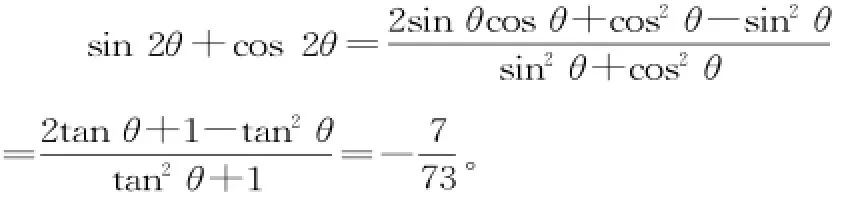
19.假设方程f(x)=0有负根x0(x0≠-1),则x0＜0且x0≠-1,f(x0)=0。

又因为a＞1,所以0＜ax0＜1,因此0＜与假设x0＜0且 x0≠-1矛盾,因此,方程f(x)=0没有负数根。

(2)假设n=k(k≥2,且k∈N+)时命题成立,即

故命题成立。

由(1)(2)知,原不等式在n∈N+,n≥2时均成立。

21.假设(1-a)b,(1-b)c,(1-c)a三个值均大于。

22.(1)f(6)=91,f(10)=271。

f(2)-f(1)=7-1=6。

f(3)-f(2)=19-7=2×6。

f(4)-f(3)=37-19=3×6。

f(5)-f(4)=61-37=4×6。

因此,当n≥2时,有f(n)-f(n-1)=6(n -1)。

f(n)=[f(n)-f(n-1)]+[f(n-1)-f(n -2)]+…+[f(2)-f(1)]+f(1)

=6[(n-1)+(n-2)+…+2+1]+1

=3n2-3n+1。

又f(1)=1=3×12-3×1+1,所以f(n)= 3n2-3n+1。

(责任编辑 徐利杰)