四自由度两模式并联机构结构综合与位置分析

石志新 叶梅燕 罗玉峰 杨廷力

(1.南昌大学机电工程学院， 南昌 330031； 2.南昌大学理学院， 南昌 330031；3.中国金陵石化公司， 南京 210037)

四自由度两模式并联机构结构综合与位置分析

石志新1叶梅燕2罗玉峰1杨廷力3

(1.南昌大学机电工程学院， 南昌 330031； 2.南昌大学理学院， 南昌 330031；3.中国金陵石化公司， 南京 210037)

为设计可实现一机多用的并联机构，提出了多模式并联机构的结构类型综合方法以及操作模式分析方法。首先利用方位特征集方法，综合得到一类(640种)具有运动分岔特性的4自由度并联机构；然后从中优选出一种机构进行操作模式分析，分析结果表明：机构处于分岔奇异点时动平台瞬时自由度为5，此时采用冗余驱动的方法可引导动平台通过分岔奇异点顺利到达三平移一转动或两平移两转动模式；最后推导了该并联机构处于上述2种操作模式时的位置正、逆解分析方程，得知位置逆解方程和三平移一转动模式时的位置正解方程均可解析求解。

并联机构； 运动分岔； 操作模式； 位置分析

引言

并联机构在理论研究和实际应用方面均已取得重要进展，但大多数研究集中于具有确定自由度的并联机构。对于具有连续变自由度或运动分岔特性的并联机构，其研究尚不够系统和深入。

运动分岔是指当机构处于某些特殊位型(称为分岔奇异点)时，动平台存在多种可能运动，此时改变某些关节变量可使动平台进入不同的连续运动空间(模式)。运动分岔这一概念最早由WOHLHART[1]于1996年提出，随后的研究主要集中于运动转向机构[2-3]和运动限定机构[4-9]，直到2006年才由FANGHELLA等[10]提出几种具有运动分岔特性的并联机构，2007年REFAAT等[11]研制了具有运动分岔特性的并联机床。KONG等[12-15]提出了3自由度多模式并联机构的构型分析与综合方法；李秦川等[16-17]基于群论综合出了一类具有运动分岔特性的并联机构；叶伟等[18]提出了一种具有4种模式(三平移、三转动、两平移一转动和两转动一平移)的并联机构；LATIFAH等[19]分析了4-RUU型并联机构的3种不同模式。

方位特征集方法在拓扑结构综合方面具有显著特点[20-22]，然而目前相关文献仅研究了确定自由度的并联机构综合，本文将该方法推广应用于连续变自由度(运动分岔特性)机构的结构综合，提出一类具有运动分岔特性的4自由度并联机构，该类机构存在三平移一转动和两平移两转动两种模式；最后从中优选一种机构，对其运动分岔特性和位置正逆解进行详细分析。

1 机构结构综合

1.1 支链的构造

(1)由于动平台是在各支链共同作用下完成运动的，故支链的方位特征集Mi应包含动平台的方位特征集M，即Mi应满足

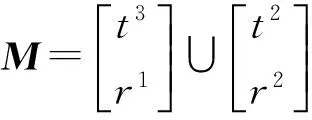
(1)

式中t3——空间三维平移r1——一维转动t2——二维平移r2——二维转动

(2)欲使动平台能够进入2种不同的连续运动模式(即三平移一转动和两平移两转动)，则至少存在1条具有连续变自由度的支链。文献[20]已给出满足式(1)的具有确定自由度的支链，故仅需构造满足要求的变自由度支链。

注意到三平移一转动和两平移两转动的交集为两平移一转动。为使问题简化，将两平移一转动对应的结构指定为一平面子链(3R、RPR、PRR、PPR)。如果在平面子链两端分别联接一个转动副，则可构造满足要求的变自由度支链(表1)。当上述两转动副轴线保持平行时，该支链方位特征集为三平移一转动；当两转动副轴线不平行时，方位特征集则为三转动两平移。

表1 支链结构类型

Tab.1 Structure types of limb

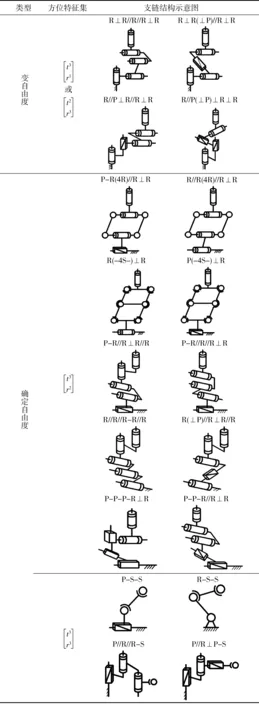
表1中的符号含义为：“∥”表示平行；“⊥”表示垂直；“-”表示交叉且不垂直；“4R”表示平行四边形机构；“4S”表示由4个球副和2个转动副构成的平行四边形机构。

1.2 具有分岔特性的四自由度并联机构

若从表1中分别取1条变自由度支链、1条三平移两转动和2条三平移三转动的确定自由度支链进行装配，则共可得到640(4×10×42)种存在2种模式(三平移一转动和两平移两转动)的四自由度并联机构。

综合考虑运动学分析简单、装配方便等原则，从上述640种并联机构中优选一种机构进行详细描述和分析。

如图1所示，从表1所示的4条变自由度支链中选取{R11⊥R12∥R13∥R14⊥R15}作为第1条支链；从10条确定自由度(三平移两转动)支链中选取{R31∥R32(4R)∥R33⊥R34}作为第3条支链；从4条确定自由度(三平移三转动)支链中选取{P21∥R22∥R23-S24}和{P41∥R22∥R23-S24}分别作为第2条和第4条支链。

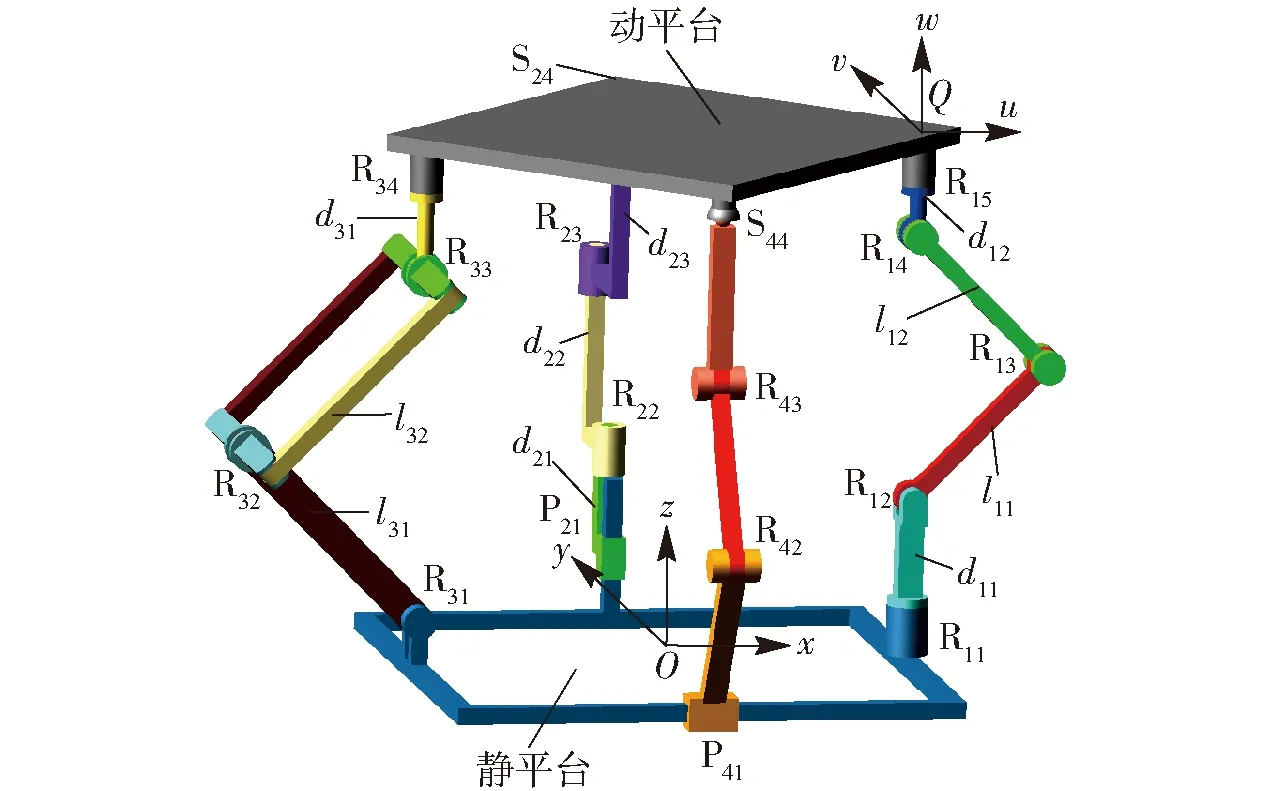
图1 机构简图及坐标系Fig.1 Schematic diagram and coordinate systems

不失一般性，设动、静平台均呈正方形形状。静平台上4个运动副(R11、P21、R31、P41)均匀分布在4条边中点处，且它们的方位配置关系为：R11和P21的轴线均垂直于静平台，R31和P41的轴线分别平行于各自所在的边。动平台上的运动副(R15、S24、R34、S44)分布在4个顶点处，且转动副R15和R34的轴线均垂直于动平台。装配初始位形时，动、静平台相互平行，且转动副R12和R31的轴线相互平行。

为描述方便，在静、动平台上分别建立静坐标系Oxyz和动坐标系Quvw。其中，原点O位于静平台的中心，x轴和y轴分别平行于静平台相邻两边，z轴为静平台所在平面的法线；原点Q与动平台上R15重合，u轴与R34和R15的连线重合，v轴与S24和S44的连线平行，w轴为动平台所在平面的法线。

2 方位特征集分析及模式切换

2.1 初始位形时动平台方位特征集分析

当机构处于初始位形(图1)时，动、静平台相互平行，且转动副R12和R31的轴线相互平行。此时，R11∥R15∥R34∥z轴∥w轴且R12∥R31∥y轴∥v轴。因此，4条支链的方位特征集Mi分别为

(2)

式中r2(∥◇(v,w))表示存在二维转动，且转动轴平行于v轴与w轴张成的平面。

动平台的方位特征集M为

(3)

式(3)表明：在初始位形时机构瞬时自由度为5，动平台具备空间三维平移以及绕v轴与w轴转动的能力。

2.2 一般位形时动平台方位特征集分析

2.2.1 动平台绕v轴连续转动

如图2所示，当动平台由初始位形绕v轴连续转动后，转动副R15和R11轴线的平行关系将被破坏，从而导致动平台丧失沿v轴平移的能力，此时动平台方位特征集M为

(4)

式中t2(⊥v)表示存在与v轴垂直的二维平移，但不能沿v轴平移。

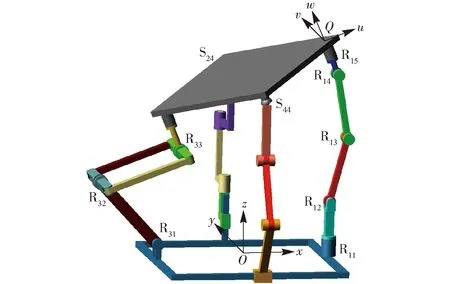
图2 两平移两转动模式Fig.2 2T2R operation mode

式(4)表明：动平台一旦由初始位形绕v轴连续转动后，将会丧失沿v轴平移的能力，机构随即进入两平移两转动模式。

2.2.2 动平台沿v轴平移

如图3所示，当动平台由初始位形沿v轴平移后，动、静平台仍相互平行，转动副R15和R11轴线的平行关系得以维系，但转动副R12和R31的轴线将不再平行，从而导致动平台丧失绕v轴(或y轴)转动的能力，此时动平台方位特征集M为

(5)

式中r1(∥w)表示存在一维转动，且转动轴平行于w轴。

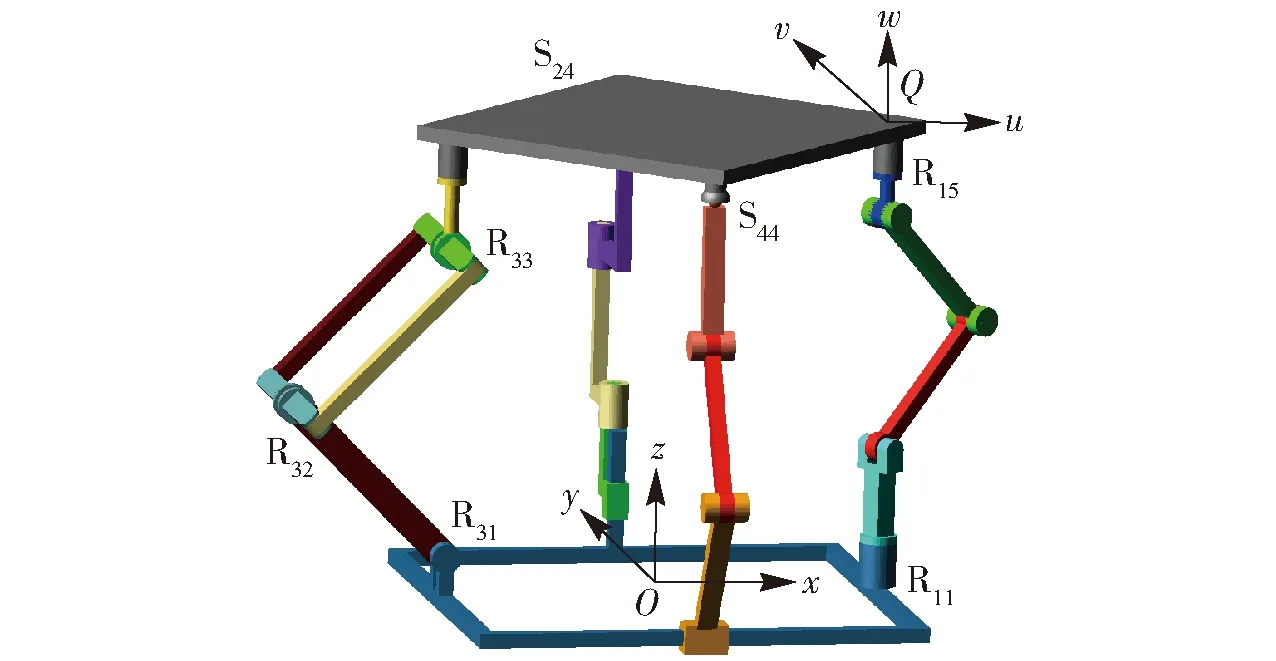
图3 三平移一转动模式Fig.3 3T1R operation mode

式(5)表明：动平台一旦由初始位形沿v轴平移后，将会丧失绕v轴转动的能力，机构随即进入三平移一转动模式。

2.3 模式切换

根据上述方位特征集分析可知：尽管在初始位形时动平台具备空间三维平移以及绕v轴与w轴转动的能力，但动平台绕v轴转动与沿v轴平移的自由度互斥，即动平台由初始位形绕v轴转动后，将不能沿v轴平移，反之亦然。因此，只有当机构处于初始位形时，才可以完成2种模式(两平移两转动和三平移一转动)间的切换。

由于机构在初始位形时瞬时自由度为5，故此时需要安装5个驱动器才能实现动平台完全可控。根据驱动副判断准则[20]，本文选取R11、R12、P21、R31、P41作为驱动副。

注意到机构在一般位形时自由度为4，因此上述驱动器中某些驱动器的作用在于引导动平台通过初始位形顺利到达指定模式，一旦动平台到达指定模式后，将会出现冗余驱动，需锁定或松开某一驱动器。例如，在初始位形时锁定R11同时驱动R12、P21、R31、P41，则机构进入两平移两转动模式；若驱动R11且松开安装在R12上的驱动器，则机构进入三平移一转动模式。

3 位置分析

如图1所示，该并联机构的结构参数为：动平台外接圆半径和静平台内切圆半径分别记为r1、r2；转动副R11、R15、R22、R23、R34以及移动副P21的轴长分别记为d11、d12、d22、d23、d31以及d21；转动副R12、R13、R31的杆长分别记为l11、l12、l31，R32与R33之间的距离记为l32。上述结构参数均为常数。

3.1 两平移两转动模式下的位置分析

机构处于该模式时(图2)，动平台的位置(Q在静坐标系中的坐标)可记为(x,0,z)，姿态(动平台依次绕v轴和w轴转过的角度)记为(β,γ)。4个驱动副(R12、P21、R31、P41)的输入量分别记为φ12、Δ2、φ3、Δ4。位置分析问题可描述为：已知结构参数，确定(x,z,β,γ)与(φ12,Δ2,φ3,Δ4)之间的映射关系。分析过程如下。

(1)根据动平台的位姿(x,z,β,γ)，可求得单位矢量u、v、w以及R14、S24、R33、S44在静坐标系的坐标，其矢量形式分别为

(6)

(2)R13、R32在静坐标系上的坐标，可用φ12、φ3方便地解析表示为

(7)

(3)由于R13与R14之间的距离恒为l12，R32与R33之间的距离恒为l32，S24的z轴坐标分量为Δ2+d21+d22+d23，S44的x轴坐标分量为Δ4，故可得约束方程组

(8)

其中

D=d21+d22+d23

(4)将式(6)、(7)代入式(8)中，且将φ12、Δ2、φ3、Δ4视为变量，而x、z、β、γ视为已知量，分离已知量和变量，可得位置逆解方程组为

(9)

其中

a1=-2l11(x-r2-d12sinβ)

b1=-2l11(z-d11-d12cosβ)

(z-d11)2-2(z-d11)d12cosβ

a2=-2l31(x+r2-2r1cosβcosγ-d31sinβ)

b2=-2l31(z+2r1sinβcosγ-d31cosβ)

显然式(9)可解析求解，且φ12与φ3均有2组解，Δ2与Δ4仅有1组解。因此，该机构位置逆解方程共有4组解。

(5)将式(8)中x、z、β、γ视为变量，而φ12、Δ2、φ3、Δ4视为已知量，分离已知量和变量且经化简后，可得位置正解方程组为

(10)

其中e1=r1(cosγ-sinγ)f1=r1(cosγ+sinγ)

h1=Δ4-r2-l11cosφ12h2=d11+l11sinφ12-Δ2-D

h3=l31cosφ3-Δ4-r2h4=Δ2+D-l31sinφ3

A1=e1cosβ-d12sinβ+h1

B1=f1sinβ+d12cosβ+h2

A2=f1cosβ+d31sinβ+h3

B2=e1sinβ-d31cosβ+h4

式(10)不可解析求解，可采用遍历搜索法[23]进行求解。

3.2 三平移一转动模式下的位置分析

机构处于该模式时(图3)，动平台位置(Q在静坐标系中的坐标)可记为(x,y,z)，姿态(动平台绕w轴转过的角度)记为θ。4个驱动副(R11、P21、R31、P41)的输入量分别记为φ11、Δ2、φ3、Δ4。则位置分析问题可描述为：已知结构参数，确定(x,y,z,θ)与(φ11,Δ2,φ3,Δ4)之间的映射关系。

位置分析过程和两平移两转动模式类似，但此时单位矢量u、v、w为

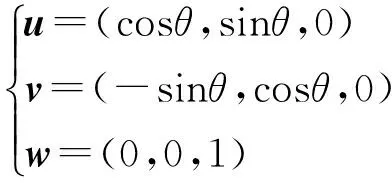
(11)

位置逆解方程组为

(12)

其中

a3=-2l31(x+r2-2r1cosθ)

b3=-2l31(z-d31)

c3=(x+r2)2+(z-d31)2-4r1[(x+r2)cosθ+

式(12)可解析求解，且φ11与φ3均有2组解，Δ2与Δ4仅有1组解。因此该机构位置逆解方程共有4组解。

位置正解方程组为

(13)

其中

A3=r1(cosθ+sinθ)-Δ4-r2+l31cosφ3

B3=r1[tanφ11cosθ-(2+tanφ11)sinθ]+

(Δ4-r2)tanφ11

值得注意的是，式(13)中第2个方程最高次数项为cos2θ。若采用半角变换，则可变为一元四次代数方程，可解析求解。因此机构位置正解方程存在4组解。

3.3 数值实例

如图1所示，并联机器人机构的结构参数分别选为：r1=r2=1.0 m，l11=l12=l31=l32=1.0 m，d11=d12=d31=d21=d22=d23=0.5 m。两平移两转动模式下4个驱动副输入量分别取为：Δ2=0.1 m，Δ4=0.2 m，φ12=φ3=60°；三平移一转动模式下的4个驱动副输入量分别取为：Δ2=0.1 m，Δ4=0.2 m，φ11=φ3=60°。

根据上述位置正解模型和方程求解算法，利用Matlab软件编程计算，可求得两平移两转动模式下的全部6组实数解(表2)，三平移一转动模式下的全部2组实数解(表3)。对应的装配构型如图4、5所示。

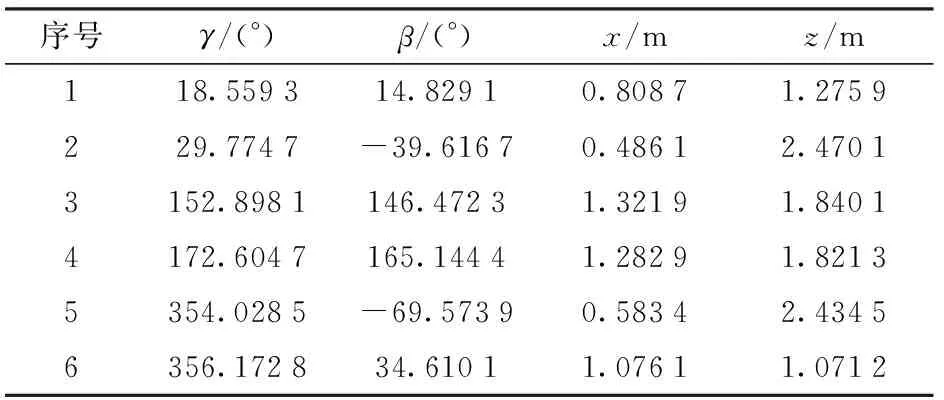
表2 两平移两转动模式下位置正解

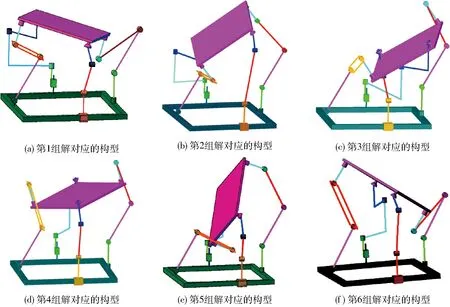
图4 表2对应的装配构型图Fig.4 Corresponding configurations of Tab.2

序号γ/(°)x/my/mz/m116.77490.8688-0.22721.60002-9.95951.35790.61991.6000

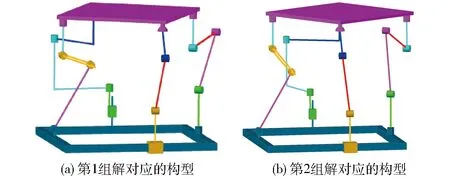
图5 表3对应的装配构型图Fig.5 Corresponding configurations of Tab.3

4 结论

(1)通过构造变自由度支链的方法，可将方位特征集方法推广应用于连续变自由度(运动分岔特性)机构的拓扑结构综合。利用改进的方位特征集方法综合得到一类(640种)具有2种操作模式的四自由度并联机构。

(2)采用冗余驱动方法，可保证综合得到的双

操作模式并联机构在2种不同操作模式(三平移一转动和两平移两转动)间快速切换，从而无需重新装配即可达到一机多用的效果。在存在多种不同操作工位需求的场合(如抓取、加工、定位装配等工艺)下，综合得到的并联机构具有重要应用开发价值。

(3)推导了机构处于2种操作模式时的位置正、逆解方程，发现2种操作模式时的位置逆解方程和三平移一转动模式时的位置正解方程均可解析求解，这有利于运动控制。

1 WOHLHART K. Kinematotropic mechanisms [M]. Dordrecht: Kluwer Academic Publishers, 1996.

2 GALLETTI C, FANGHELLA P. Single-loop kinematotropic mechanisms [J]. Mechanism and Machine Theory, 2001, 36(6): 743-761.

3 GALLETTI C, GIANNOTTI E. Multiloop kinematotropic mechanisms [C]∥International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2002: 455-460.

4 LEE C C, HERVÉ J M. Discontinuous mobility of one family of spatial 6R mechanisms through the group algebraic structure of displacement set [C]∥International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2002: 645-653.

5 LEE C C, HERVÉ J M. Discontinuously movable seven-link mechanisms via group-algebraic approach [J]. Proc. IMech E, Part C: Journal of Mechanical Engineering Science, 2005, 219(6): 577-587.

6 YAN H, KUO C. Topological representations and characteristics of variable kinematic joints [J]. ASME Journal of Mechanical Design, 2006, 128(2)：384-391.

7 LEE C C, HERVÉ J M. Discontinuously movable 8R mechanisms with an infinity of bifurcations [C]∥The 12th World Congress in Mechanism and Machine Science, 2007: 198-203.

8 LEE C C, HERVÉ J M. A novel discontinuously movable six-revolute mechanism [C]∥International Conference on Reconfigurable Mechanisms and Robots, 2009: 58-62.

9 KONG X, HUANG C. Type synthesis of single-DOF single-loop mechanisms with two operation modes [C]∥International Conference on Reconfigurable Mechanisms and Robots, 2009: 136-141.

10 FANGHELLA P, GALLETTI C, GIANNOTTI E. Parallel robots that change their group of motion [M]. Netherlands: Springer, 2006.

11 REFAAT S, HERVÉ J M, NAHAVANDI S, et a1. Two mode overconstrained three DOFs rotational translational linear motor based parallel kinematics mechanism for machine tool applications [J]. Robotica, 2007, 25(4): 461-466.

12 KONG X, GOSSELIN C, RICHARD P L. Type synthesis of parallel mechanisms with multiple operation modes [J]. ASME Journal of Mechanical Design, 2007, 129(6): 595-601.

13 KONG X. Type synthesis of 3-DOF parallel mechanisms with both a planar operation mode and a spatial translational operation mode [J]. ASME Journal of Mechanisms and Robotics, 2013, 5(4): 041015-041015-12.

14 KONG X. Reconfiguration analysis of a 3-DOF parallel mechanism using Euler parameter quaternions and algebraic geometry method [J]. Mechanism and Machine Theory, 2014, 74(1): 188-201.

15 KONG X, YAN J. Type synthesis of 3-DOF multi-mode translational/spherical parallel mechanisms with lockable joints [J]. Mechanism and Machine Theory, 2016, 96(1): 323-333.

16 李秦川，陈巧红，武传宇，等.变自由度4-xPxRxRxRyRN并联机构[J].机械工程学报，2009，45(1)：83-87. LI Qinchuan, CHEN Qiaohong, WU Chuanyu, et al. 4-xPxRxRxRyRNparallel mechanism with variable mobility [J]. Chinese Journal of Mechanical Engineering, 2009, 45(1): 83-87. (in Chinese)

17 LI Q, HERVÉ J M. Parallel mechanisms with bifurcation of schoenflies motion [J]. IEEE Transactions on Robotics, 2009, 25(1): 158-164.

18 叶伟，方跃法，郭盛，等. 一种新型并联机构的运动分岔特性及运动学分析[J].机械工程学报，2013，49(13)：8-15. YE Wei, FANG Yuefa, GUO Sheng, et al. Bifurcated motion and kinematics of novel parallel mechanism [J]. Journal of Mechanical Engineering, 2013, 49(13): 8-15. (in Chinese)

19 LATIFAH N, STEPHANE C, PHILEPPE W, et al. Reconfiguration analysis of a 4-RUU parallel manipulator [J]. Mechanism and Machine Theory, 2016, 96(1): 269-289.

20 杨廷力，刘安心，罗玉峰，等. 机器人机构拓扑结构设计[M].北京：科学出版社，2012.

21 杨廷力，沈惠平，刘安心，等.机构自由度公式的基本形式、自由度分析及其物理内涵[J].机械工程学报, 2015, 51(13): 69-80. YANG Tingli, SHEN Huiping, LIU Anxin, et al. Review of the formulas for degrees of freedom in the past ten years [J]. Journal of Mechanical Engineering, 2015, 51(13): 69-80. (in Chinese)

22 沈惠平，尹洪波，李菊，等.基于方位特征方法的范例并联机构的拓扑特征分析及其启示与应用[J].机械工程学报, 2015, 51(13): 101-115. SHEN Huiping, YIN Hongbo, LI Ju, et al. Position and orientation characteristic based method and enlightenment for topology characteristic analysis of typical parallel mechanisms and its application [J]. Journal of Mechanical Engineering, 2015, 51(13): 101-115. (in Chinese)

23 石志新，叶梅燕，毛志伟，等. 5-5型并联机器人位置正解的简单算法[J/OL]. 农业机械学报，2014，45(3)：314-319.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20140351&flag=1.DOI:10.6041/j.issn.1000-1298.2014.03.051. SHI Zhixin, YE Meiyan, MAO Zhiwei, et al. Simple method for forward displacement analysis of a 5-5 in-parallel robot[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(3): 314-319. (in Chinese)

Type Synthesis and Position Analysis of 4-DOF Parallel Mechanisms with Two Operation Modes

SHI Zhixin1YE Meiyan2LUO Yufeng1YANG Tingli3

(1.SchoolofMechanicalandElectronicEngineering,NanchangUniversity,Nanchang330031,China2.SchoolofScience,NanchangUniversity,Nanchang330031,China3.JinlingPetrochemicalCorporation,Nanjing210037,China)

To develop reconfigurable manufacturing systems with a short changeover time, parallel mechanisms with multiple operation modes had received much attention from researchers. However, the current researches on multiple modes were mostly concentrated on the 3-DOF parallel mechanisms. A simple method of type synthesis and operation mode analysis for 4-DOF parallel mechanisms with both two-dimension translation and two-dimension rotational operation mode and three-dimension translation and one-dimension rotational operation mode was put forward. Type synthesis of 4-DOF parallel mechanisms was introduced based on the theory of position and orientation characteristics. And one family of 4-DOF parallel mechanisms with two operation modes was presented. Then, one topology was selected from the different possibilities of parallel manipulators after imposing some practical requirements. The selected parallel manipulator had instantaneously five degrees of freedom at the constraint singular configuration. The parallel manipulator must pass through singular configuration when it was switched from one operation mode to another. Redundant actuators were used to ensure that the parallel manipulator can pass through the singular configuration. Finally, the forward and inverse kinematic equations of the parallel manipulator with bifurcated motion in different operation modes were derived. The parallel manipulator presented was intended to be used in manufacturing application.

parallel mechanism; bifurcated motion; operation mode; position analysis

10.6041/j.issn.1000-1298.2017.04.051

2016-08-02

2016-10-18

国家自然科学基金项目(51365036、51475050)

石志新(1979—)，男，副教授，博士，主要从事机器人机构学研究，E-mail: shizhixin@ncu.edu.cn

TH112

A

1000-1298(2017)04-0383-07