Exe-Variant并联模块静刚度分析
2017-06-05陶兆胜赵艳芹
陶兆胜 彭 澎 赵艳芹
(安徽工业大学机械工程学院, 马鞍山 243032)
Exe-Variant并联模块静刚度分析
陶兆胜 彭 澎 赵艳芹
(安徽工业大学机械工程学院, 马鞍山 243032)
由于良好的刚度和动力学性能,Exechon并联机构已被应用于加工、制造、航空航天等领域,但Exechon并联模块的转动能力较弱,导致其工作空间较小。为此,以机构变异方法设计构型为2RPU&1RPS的Exe-Variant并联模块。为研究Exe-Variant并联模块的刚度性能,采用子结构综合技术建立了该并联模块的刚度模型。建模时,将机构划分成若干子系统,并计入关节和支链弹性对整机刚度的影响。基于所建刚度模型,研究了Exe-Variant并联模块整机刚度在其工作空间内的分布特性,并进行了机构关键设计参数和机构关节处弹性变形对整机刚度的影响分析。结果表明,该模块的刚度分布在工作全域内呈现出对称性,模块关键设计参数和机构关节处弹性变形对整机的刚度性能影响较大。
Exe-Variant; 并联机构; 静刚度; 子结构综合
引言
Exechon并联模块作为少自由度的2UPR&1SPR并联机构,国内外学者对其运动学、刚度以及动力学开展了大量研究[1-11]。HUANG等[12]借助有限元软件对Exechon的工作全域进行了动力学仿真研究。LIAN等[13]基于子结构综合结合雅克比矩阵和相互关联转动关节的变形影响考虑机构的刚度映射。在设计阶段,曲海波等[14-15]运用半解析模型快速预估工作全域内的刚度特性。LI等[16]运用旋量理论和虚功原理建立ExechonX150的刚度模型,分析机构特定位姿下的刚度并将其与有限元仿真做了对比。陈修龙等[17]采用ADAMS软件对5自由度并联机构的运动学进行了模拟仿真。季晔等[18]建立了4-SPxyzS/PxPzUxz并联机构的位置和姿态工作空间,并提出“点集”近似计算和敏感度概论,利用数值法求解了位置工作空间大小和姿态工作空间范围与机构尺度参数之间的关系。
笔者团队在前期研究中,采用机构变异方法设计Exe-Variant并联模块并进行了刚度建模研究[19-20]。在此基础上,本文研究Exe-Variant并联模块在工作全域的静刚度映射,并进行其静刚度参数影响分析,以期为改善该并联模块的刚度性能提供一定的理论依据。
1 机构描述
Exe-Variant动力头主要由2自由度串联转头和Exe-Variant并联模块组成,如图1所示。其中,Exe-Variant并联模块主要由动平台、静平台和3条过约束支链组成。支链1和支链2的拓扑结构相同,分别通过转动副R、虎克铰U与静平台、动平台连接。支链3的结构与支链1、2略有不同,其通过球铰S副与动平台相连。

图1 Exe-Variant实体模型Fig.1 Model of Exe-Variant
从机构学的角度来看,Exe-Variant并联模块的拓扑结构为2RPU&1RPS,其机构简图如图2所示。图中,△A1A2A3和△B1B2B3分别表示动平台及基座,且设定为等腰直角三角形,其中∠A1A3A2=∠B1B3B2=90°。A1、A2分别表示支链1、2上虎克铰的几何中心;A3表示支链3上球铰的几何中心;Bi(i=1,2,3)表示支链i上转动副的几何中心;Ci(i=1,2,3)表示支链i末端[20]。
2 静刚度预估与分析参数
根据Exe-Variant并联模块的结构特点,将系统划分成动平台子系统、支链子系统和基座子系统。由于动平台和基座的刚度相对较大,故建模时将其视为刚体。为计入支链柔度和复杂结构对系统刚性的影响,采用有限元的思想将支链划分成具体等效截面的空间梁,如图3所示。
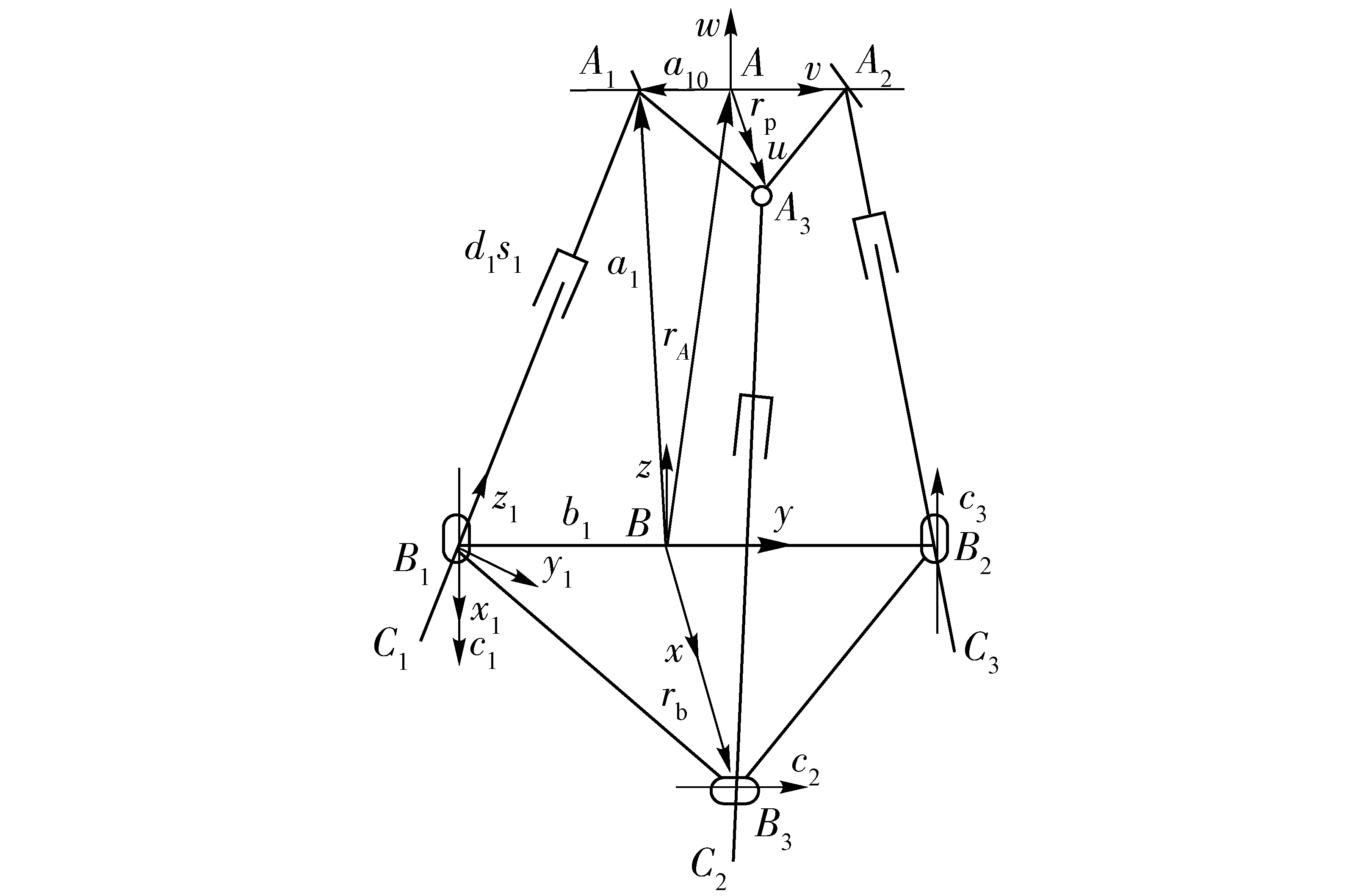
图2 Exe-Variant机构简图Fig.2 Schematic diagram of Exe-Variant PKM

图3 支链的装配示意图Fig.3 Assembling scheme of an individual limb1.球铰/虎克铰 2.前端轴承 3.滚珠丝杠 4.导轨 5.转动副6.末端轴承 7.电动机
根据支链截面的变化情况,将支链的截面处理为如图3所示的矩形截面Ⅰ和Ⅱ。其中,截面Ⅰ表示AiDi段的等效截面;截面Ⅱ表示DiCi段的等效截面。图中,w0、h0分别表示矩形截面Ⅰ的等效宽度和高度;w1、w2、h1、h2分别表示矩形截面Ⅱ的外部和内部的等效宽度和高度。
计入支链子系统和动平台子系统间的变形协调条件,可得到系统的刚度模型为
KU=W
(1)
式中U——系统在全局坐标系Bxyz下的位移矩阵
K——系统在全局坐标系Bxyz下的刚度矩阵
W——系统在全局坐标系Bxyz下的载荷矩阵
具体的推导过程可参照文献[20]。
以文献[20]的Exe-Variant并联模块为例,对其进行静刚度映射和静刚度参数影响分析。表1、2分别给出了该并联模块的几何参数和关节刚度参数[20]。
表1中,s为动平台的行程;l为支链的物理长度;ψmax和θmax分别为偏转角ψ和θ的最大值。

表1 Exe-Variant并联模块几何结构参数

图4 工作平面z=1 200 mm上Exe-Variant并联模块的静刚度映射Fig.4 Stiffness distributions over work plane of z=1 200 mm

参数kulx0/(N·μm-1)kuly0/(N·μm-1)kulz0/(N·μm-1)数值112214100参数kulw0/(MN·rad-1)kusx0/(N·μm-1)kusy0/(N·μm-1)数值242323参数kusz0/(N·μm-1)kusw0/(MN·rad-1)kucx0/(N·μm-1)数值62318676参数kucy0/(N·μm-1)kucz0/(N·μm-1)kucw0/(MN·rad-1)数值44634818参数krx0/(N·μm-1)kry0/(N·μm-1)krz0/(N·μm-1)数值3805301006参数krv0/(MN·rad-1)krw0/(MN·rad-1)kslx0/(N·μm-1)数值1818112参数ksly0/(N·μm-1)kslz0/(N·μm-1)kssx0/(N·μm-1)数值21410023参数kssy0/(N·μm-1)kssz0/(N·μm-1)kscx0/(N·μm-1)数值23623676参数kscy0/(N·μm-1)kscz0/(N·μm-1)数值446348
各关节在其连体坐标系下的刚度如表2所示。
表2中,kuij(i=l,s,c;j=x,y,z,w)分别为虎克铰长轴l、短轴s和交叉轴c在3个正交方向的线刚度和角刚度;krx0、kry0和krz0分别为转动副在3个正交方向的线刚度;krv0和krw0分别为转动副绕其自身坐标系y和z轴的角刚度;ksij(i=l,s,c;j=x,y,z)分别为球铰长轴l、短轴s和交叉轴c在3个正交方向的线刚度。
3 工作空间内的静刚度映射
为分析Exe-Variant并联模块的静刚度映射,采用“分层切片”思想,将工作空间离散成若干个工作平面,再结合运动学逆解获得各工作平面上任一点所对应的机构位姿下的静刚度。本文选取其工作平面为z=1 200 mm,分析在u、v和w方向的主刚度分布,如图4所示。
由图4可知,Exe-Variant并联模块各方向刚度随位姿变化。其中,u方向的线刚度k11的变化范围为[9.75, 73.4] MN/m;v方向的线刚度k22的变化范围为[14.2, 57.4] MN/m;w方向的线刚度k33的变化范围为[88.5, 169] MN/m;u方向角刚度k44的变化范围为[35.1, 44.5] MN·m/rad;v方向角刚度k55的变化范围为[23.9, 29.3] MN·m/rad;w方向角刚度k66的变化范围为[3.4, 20.9] MN·m/rad。Exe-Variant并联模块各方向刚度关于平面ψ=0°对称分布,这与初始位置时支链1、2关于支链3对称这一结构特点有关。该并联模块w方向的线刚度k33较其他2个方向的线刚度大得多,而该方向的角刚度k66较其他2个方向的角刚度小得多,表明该模块在轴向具有较强的抵抗外力变形的能力。
由图4也可知,Exe-Variant并联模块同一方向的线刚度和角刚度呈现出开口方向相反的规律。例如,Exe-Variant并联模块u方向的线刚度k11在θ=0°两侧随着θ绝对值的增大而增大(开口向上),而u方向的角刚度k44在θ=0°两侧随着θ绝对值的增大而减小(开口向下);v方向的线刚度k22在ψ=0°两侧随着ψ绝对值的增大而增大(开口向上),v方向的角刚度k55的ψ=0°两侧随着ψ绝对值的增大而减小(开口向下);w方向的线刚度k33开口向下,w方向的角刚度k66开口向上。
4 静刚度参数影响分析
图5所示为Exe-Variant并联模块的静刚度随动平台、基座半径的变化曲面。
图6所示为Exe-Variant并联模块的静刚度随支链机座截面尺寸的变化曲面。图中,δh和δw分别表示支链的等效高度和等效宽度的增量。
由图5a、5b可知,Exe-Variant并联模块u方向的线刚度k11以及v方向的线刚度k22均随着动平台
半径rp的增大而减小,随着基座半径rb的增大而增大。由图5c、5f可知,w方向的线刚度k33以及该方向的角刚度k66均随着动平台半径rp的增大而增大,随着基座半径rb的增大而减小。由图5d、5e可知,u方向的角刚度k44以及v方向的角刚度k55均随着动平台半径rp和基座半径rb的增大而增大。另外,动平台半径rp和基座半径rb对各方向静刚度的影响程度不同。例如,动平台半径rp对w方向的线刚度k33以及该方向的角刚度k66的影响较大,而对其他方向的刚度影响较小;而基座半径rb对u方向的线刚度k11及该方向的角刚度k44、v方向的线刚度k22及该方向的角刚度k55

图5 Exe-Variant并联模块的静刚度随动平台、基座半径的变化曲面Fig.5 Variations of stiffness with respect to radii of platform and base
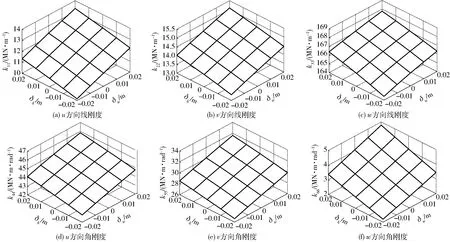
图6 Exe-Variant并联模块的静刚度随支链截面尺寸的变化曲面Fig.6 Variations of stiffness with respect to cross-section of limb body
影响较大,对其他方向的刚度影响较小。
由图6各方向静刚度随δh和δw的变化曲面可知,随支链机座截面尺寸的增大,整机刚度逐渐增大。
关节处的弹性变形对整机刚度的影响不可忽略,但因篇幅有限,现以虎克铰刚度为实例分析。定义虎克铰长轴x方向线刚度的放大因子λulx和整机刚度的放大因子ki为

图7 整机刚度比例系数随虎克铰刚度的变化曲线Fig.7 Variation curves of stiffness with respect to Hooke-joint stiffness coefficient
(2)
(3)式中kulx0——虎克铰长轴x方向初始线刚度(表2)kulx——虎克铰长轴x方向的当前线刚度kii0——模块处于初始位姿z=1 200 mm、θ=0°、ψ=0°时整机的刚度
kii——整机当前刚度
整机刚度比例系数随虎克铰刚度的变化曲线如图7所示。其中,λulx、λuly、λulz和λulw分别为长轴x、y、z3个方向的线刚度放大因子以及z方向的角刚度放大因子;λusx、λusy、λusz和λusw分别为短轴x、y、z3个方向的线刚度放大因子以及z方向的角刚度放大因子;λucx、λucy、λucz和λucw分别为交叉轴x、y、z3个方向的线刚度放大因子以及z方向的角刚度放大因子。上述放大因子数学公式定义类似式(2)。
由图7a、7e、7i可知,随着长轴、短轴、交叉轴x方向线刚度的增大,u方向线刚度k11和v方向角刚度k55以及w方向角刚度k66单调递增;由图7c、7g、7k可知,随着长轴、短轴、交叉轴z方向线刚度的增大,v方向线刚度k22、w方向线刚度k33和v方向角刚度k44逐渐增大。从以上分析可知,整机刚度随虎克铰x方向线刚度和z方向线刚度的增大而增大。而图7b、7d、7f、7h、7j、7l反映整机刚度不随长轴、短轴、交叉轴y方向线刚度和z方向角刚度的变化而变化,即球铰y方向线刚度和z方向角刚度对系统刚度无影响。从数值上进行考虑,虎克铰z方向线刚度对整机刚度的影响与x方向线刚度相比较大,故在进行虎克铰的结构设计时,需适当考虑长轴、短轴和交叉轴的z方向线刚度。
5 结论
(1) Exe-Variant并联模块在工作空间内的刚度映射表明:该机构各方向刚度关于平面电动机对称分布。
(2) 为剖析Exe-Variant并联模块的关键设计参数对整机刚度性能的作用规律,进行了静刚度的参数影响分析。分析表明:动平台半径、支链的截面尺寸和关节处的弹性变形会对整机的刚度性能产生重大影响。在进行该类少自由度并联机构的结构设计时,可适当调整该类关键设计参数以满足整机对刚度的要求。
1 HU B. Kinematically identical manipulators for the Exechon parallel manipulator and their comparison study[J]. Mechanism & Machine Theory, 2016,103:117-137.
2 JIN Z, SHI J, SARAF A, et al. Elastodynamic modeling and analysis for an Exechon parallel kinematic machine[J]. Journal of Manufacturing Science & Engineering, 2016, 138(3):7190-7200.
3 王飞博, 陈巧红, 武传宇, 等. 2-UPR-SPR并联机构尺度综合[J]. 机械工程学报, 2015, 51(21):24-32. WANG F B, CHEN Q H, WU C Y, et al. Dimensional synthesis of a 2-UPR-SPR parallel manipulator[J]. Journal of Mechanical Engineering, 2015, 51(21):24-32.(in Chinese)
4 XIE F, LIU X J, LI T. A comparison study on the orientation capability and parasitic motions of two novel articulated tool heads with parallel kinematics[J]. Advances in Mechanical Engineering, 2013,5(4):249103-249103.
5 CARBONARI L, CALLEGARI M, PALMIERI G, et al. A new class of reconfigurable parallel kinematic machines[J]. Mechanism & Machine Theory, 2014,79:173-183.
6 BI Z M. Kinetostatic modeling of Exechon parallel kinematic machine for stiffness analysis[J]. The International Journal of Advanced Manufacturing Technology, 2014, 71(1-4): 325-335.
7 SHANG M, BUTTERFIELD J, ARMSTRONG C, et al. A flexible fixture for aircraft wing assembly based on a parallel kinematic machine (Exechon)[J]. SAE International Journal of Aerospace, 2011, 4(2): 839-849.
8 PORTMAN V T, CHAPSKY V S, SHNEOR Y. Evaluation and optimization of dynamic stiffness values of the PKMs: collinear stiffness value approach[J]. Mechanism & Machine Theory, 2014, 74(6): 216-244.
9 GANESH S S, RAO A B K. Inverse dynamics of a 3-DOF translational parallel kinematic machine[J]. Journal of Mechanical Science & Technology, 2015, 29(11): 4583-4591.
10 XIE F G, LIU X J, WANG C. Design of a novel 3-DOF parallel kinematic mechanism: type synthesis and kinematic optimization[J]. Robotica, 2014, 33(3): 622-637.
11 TYAPIN I, HOVELAND G. The Gantry-Tau parallel kinematic machine-kinematic and elastodynamic design optimization[J]. Meccanica, 2011, 46(1): 113-129.
12 HUANG T, WANG P F, ZHAO X M, et al. Design of a 4-DOF hybrid PKM module for large structural component assembly[J]. CIRP Annals-Manufacturing Technology, 2010, 59(1): 159-162.
13 LIAN B B, SUN T, SONG Y M, et al. Stiffness analysis and experiment of a novel 5-DOF parallel kinematic machine considering gravitational effects[J]. International Journal of Machine Tools and Manufacture, 2015, 95: 82-96.
14 曲海波, 梁艺瀚, 方跃法, 等. 4-RRS冗余球面并联机构的静力学与刚度分析[J]. 机械工程学报, 2015, 51(11): 8-15. QU H B, LIANG Y H, FANG Y F, et al. Static stiffness analysis of 4-RRS redundant spherical parallel mechanism[J]. Journal of Mechanical Engineering, 2015, 51(11): 8-15.(in Chinese)
15 汪满新, 王攀峰, 宋轶民, 等. 4自由度混联机器人静刚度分析[J]. 机械工程学报, 2011, 47(15): 9-16. WANG M X, WANG P F, SONG Y M, et al. Stiffness analysis of a 4-DOF hybrid robot [J]. Journal of Mechanical Engineering, 2011, 47(15): 9-16.(in Chinese)16 LI X, ZLATANOV D, ZOPPI M, et al. Stiffness estimation and experiments for the Exechon parallel self-reconfiguring fixture mechanism[C]∥Proceedings of the ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2012: 637-645.
17 陈修龙, 孙先洋, 邓昱. 4-UPS-RPS空间5自由度并联机构运动学分析[J/OL]. 农业机械学报, 2013, 44(8): 257-261.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130844&flag=1. DOI:10.6041/j.issn.1000-1298.2013.08.044. CHEN X L, SUN X Y, DENG Y. Kinematics analysis of 4-UPS-RPS spatial 5-DOF parallel mechanism [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(8): 257-261.(in Chinese)
18 季晔, 刘宏昭, 原大宁. 4-SPS/PPU型并联机构工作空间与尺度分析[J/OL]. 农业机械学报, 2013, 44(11): 322-328.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20131154&flag=1. DOI:10.6041/j.issn.1000-1298.2013.11.054. JI Y, LIU H Z, YUAN D N. Workspace and scale analysis of 4-SPS/PPU parallel mechanism[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(11): 322-328.(in Chinese)
19 TANG T F, ZHAO Y Q, ZHANG J, et al. Conceptual design and workspace analysis of an Exechon-inspired parallel kinematic machine[C]∥The 3rd ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robotics, 2015:445-453.
20 路曼, 赵艳芹. 类Exechon并联模块的结构设计与刚度建模[J/OL]. 农业机械学报, 2016, 47(3): 367-388. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160352&flag=1. DOI:10.6041/j.issn.1000-1298.2016.03.052. LU M, ZHAO Y Q. Structural design and stiffness modeling for Exe-Variant parallel kinematic machine[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3): 367-388.(in Chinese)
Stiffness Analysis for Exe-Variant Parallel Kinematic Machine
TAO Zhaosheng PENG Peng ZHAO Yanqin
(SchoolofMechanicalEngineering,AnhuiUniversityofTechnology,Maanshan243032,China)
Exechon parallel kinematic machine (PKM) has been applied to machining, assembling and aerospace industries due to its high rigidity and high dynamics. However, its rotational ability is comparatively weak. In order to improve the rotational ability of the Exechon PKM, an Exe-Variant PKM was proposed whose topology was a 2RPU&1RPS parallel mechanism. And the mechanical structure of the proposed Exe-Variant PKM was designed. In order to achieve a thorough understanding of stiffness characteristics of the Exe-Variant PKM, the stiffness model of the parallel module was designed by substructure synthesis technique. According to its structure feature, the Exe-Variant PKM was divided into several subsystems, including a moving platform subsystem, three limb subsystems and a fixed base subsystem. Meanwhile, the elasticity of joints and limbs was considered. Based on the proposed stiffness model, the stiffness distributions throughout the workspace were discussed and the parameters analysis on the stiffness of an Exe-Variant PKM was conducted. Results showed that the stiffness distributions of the Exe-Variant PKM were symmetric about a certain plane throughout the workspace, and the key design parameters had a great influence on the rigidity of the Exe-Variant PKM. Furthermore, the elastic deformation of joints seemed to have a greater influence on stiffness inzdirection than those inxandydirections of the Exe-Variant PKM. It was worthy to point out that the analysis conducted can provide theoretical foundation for structure optimization.
Exe-Variant; parallel kinematic machine; stiffness; substructure synthesis
10.6041/j.issn.1000-1298.2017.04.050
2016-07-21
2016-09-02
高性能复杂制造国家重点实验室(中南大学)开放基金项目(Kfkt2013-12)
陶兆胜(1970—),男,副教授,主要从事机械设计和机器视觉研究,E-mail: trobert@ahut.edu.cn
TH112
A
1000-1298(2017)04-0377-06
