基于动态反馈A*蚁群算法的平滑路径规划方法
2017-06-05费继友刘晓东
黄 辰 费继友, 刘 洋 李 花 刘晓东
(1.大连交通大学机械工程学院, 大连 116028; 2.大连交通大学动车运用与维护工程学院, 大连 116028;3.釜庆国立大学工程学院, 釜山 608737)
基于动态反馈A*蚁群算法的平滑路径规划方法
黄 辰1费继友1,2刘 洋3李 花2刘晓东2
(1.大连交通大学机械工程学院, 大连 116028; 2.大连交通大学动车运用与维护工程学院, 大连 116028;3.釜庆国立大学工程学院, 釜山 608737)
针对移动机器人提出了一种基于动态反馈A*蚁群算法的平滑路径规划方法。首先,为了克服蚁群算法收敛速度慢的缺点,提出了简化A*算法来优化初始信息素设置以解决初次搜索的盲目性,并借鉴多策略进化机制加强算法的全局搜索能力。其次,为了进一步提高算法在路径规划中的适应能力,解决陷入局部极小和停滞问题,引入闭环反馈思想来实现参数的动态自适应调节。最后,结合三次B样条曲线对所规划的路径进行平滑处理,以满足移动机器人实际运动路径的要求。通过仿真表明:与原蚁群算法相比,动态反馈A*蚁群算法平均可减少10.4%的路径成本和65.8%的计算时长。同时,该算法在动态和静态环境中,均能快速规划出一条光滑优质路径。
路径规划; 蚁群算法; 动态反馈; A*算法; B样条曲线
引言
目前,路径规划成为移动机器人控制领域的热点之一[1-2]。除传统的规划方法,如人工势场法[3]、栅格法等,启发式智能方法由于其良好的学习能力也开始应用到移动机器人的路径规划领域[4-8]。其中,蚁群算法(AC)由于具有并行性、强鲁棒性等优点在移动机器人路径规划问题的解决中得到广泛应用,但存在收敛速度慢,易陷入局部最优以及初期信息素匮乏等现象,使得搜索比较盲目,导致收敛速度慢等问题。近年来,大部分学者开始研究对蚁群信息素更新和搜索策略的改进[9-14]。但是,对于信息素初始化,大多采取平均分配原则,导致搜索时间加长。同时,蚁群参数对规划路径的性能产生较大影响,目前大部分改进的蚁群算法在迭代过程中使用固定的参数或采用预先设计好的分段算法参数,这种参数是开环的,并不能动态地反馈搜索过程,不能很好地适应搜索空间中的不确定性。因此,解决参数优化问题的有效途径之一是闭环反馈优化。
本文提出一种基于动态反馈A*蚁群算法的平滑动态路径规划方法。首先,为提高算法搜索效率,以 A*算法的估价函数为评价标准,得到一条估价函数值相对最小的规划路径,增加此路径上的初始信息素,从而优化信息素初值。其次,采用多进化策略加大搜索空间,防止局部最优。同时,引入闭环反馈动态自适应调节算法参数,提高算法在动态路径规划中的适应能力,并解决算法的停滞问题。最后,引入三次B样条曲线对规划路径进行平滑处理。
1 A*蚁群算法与多进化机制
1.1 A*蚁群算法
蚁群算法在首次搜索时,由于地图信息的匮乏,大多采用信息素均匀分布法,将各条路径上的信息素初始化为1个常量C,从而造成算法在搜索初期由于环境未知而降低收敛速度,增加算法的搜索时间。为对初始信息素进行优化,提出利用简化的A*算法和地图信息来设置初始信息素以加快算法初期的收敛速度,减少迭代次数,提高算法的实时性。
A*算法是一种经典的启发式搜索算法[15],是静态环境中求解最短路径较为有效的直接搜索方法[16]。A*算法的估价函数为[17]
f(n)=g(n)+h(n)
(1)
其中
(2)
(3)
式中f(n)——节点n的估价函数g(n)——当前节点n到起点s的实际代价h(n)——当前节点n到目标节点g的预估代价
据此,简化A*算法的主要原理为借用A*算法的估价函数作为评价指标,从起点出发,将以起点为中心的相邻节点中的无障碍节点组成OPEN表,取估价函数值最小的节点放入CLOSE表中,再以此节点为中心,选估价函数值最小的节点放入CLOSE表中,从而迅速搜索到1条从起点到目标点估价函数相对最小的路径,即CLOSE表中节点所连接的路径。简化A*算法中不需要考虑既在父节点又在新子节点邻域内的待选节点实际估价值g(n)的再检查过程,即省略待选节点直接到父节点与通过新的子节点再到父节点的实际代价的比较过程。将f(n)作为评价函数得到的优化路径记为Rfbest,将这条路径的初始信息素设为
τ(Rfbest)=kC(k>1)
(4)
其余路径的初始信息素仍为常数C。本文将用简化A*算法来优化初始信息素,称为A*蚁群算法。
1.2 多策略进化机制
为增加蚁群搜索空间,加大算法的随机性以获得全局最优解,引入多策略进化机制。
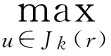
(5)
式中α——信息素启发因子β——能见度启发因子τ——信息素η——能见度或启发信息Jk(r)——下一步允许选择的栅格集
2 参数分析及动态闭环调节
2.1 参数影响分析
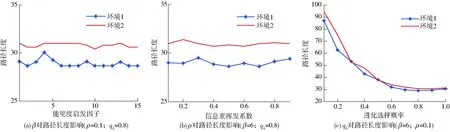
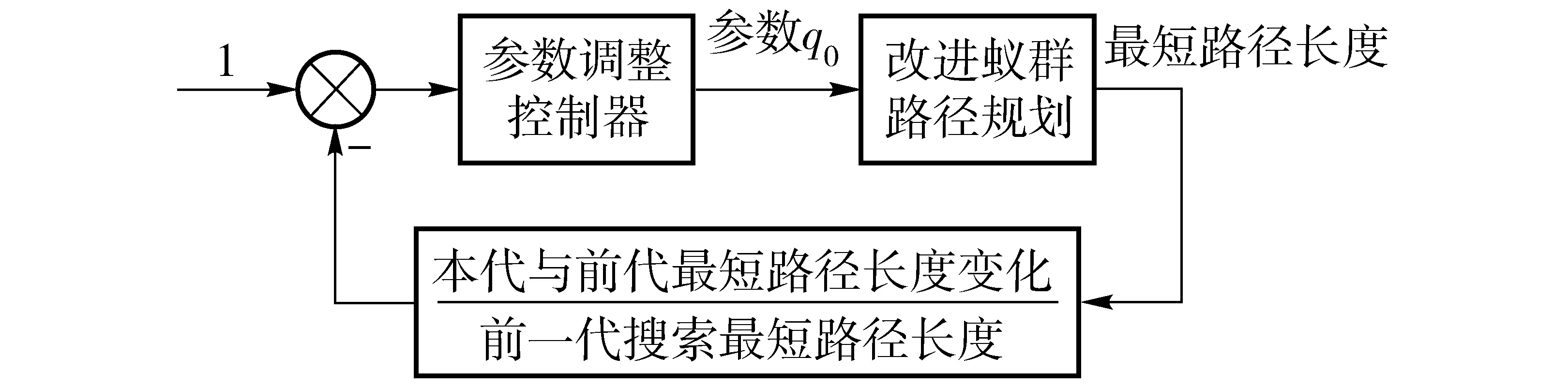
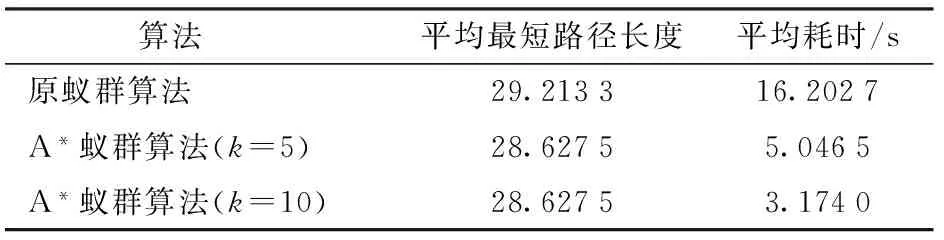
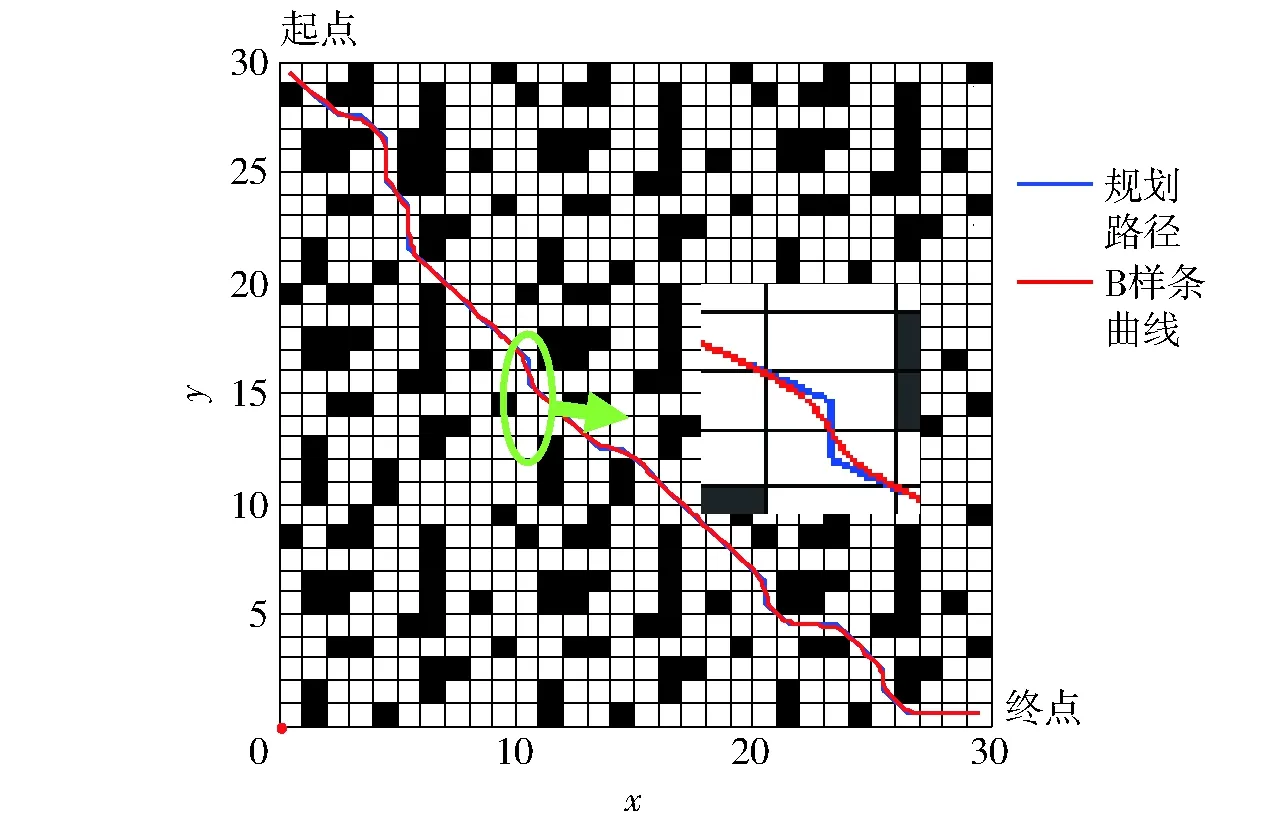
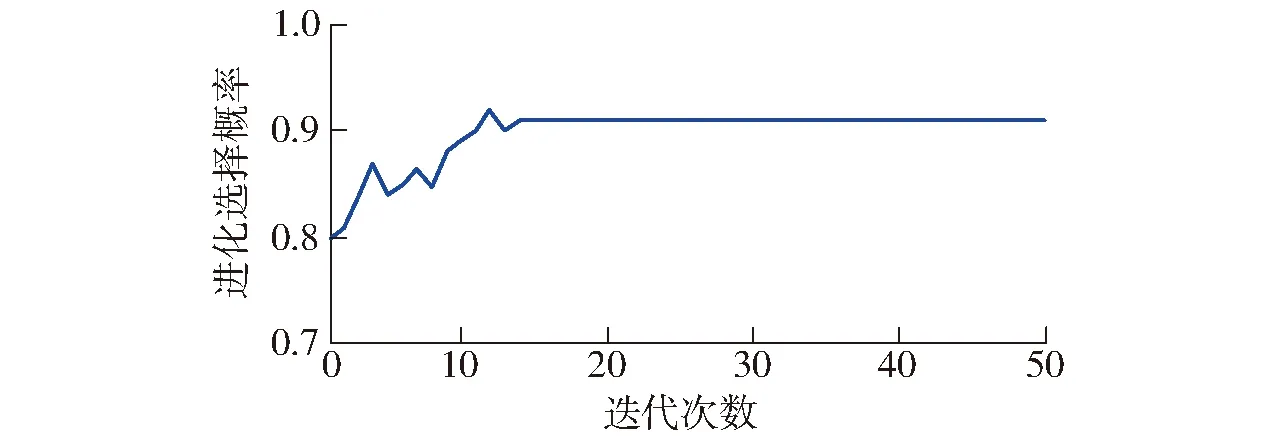
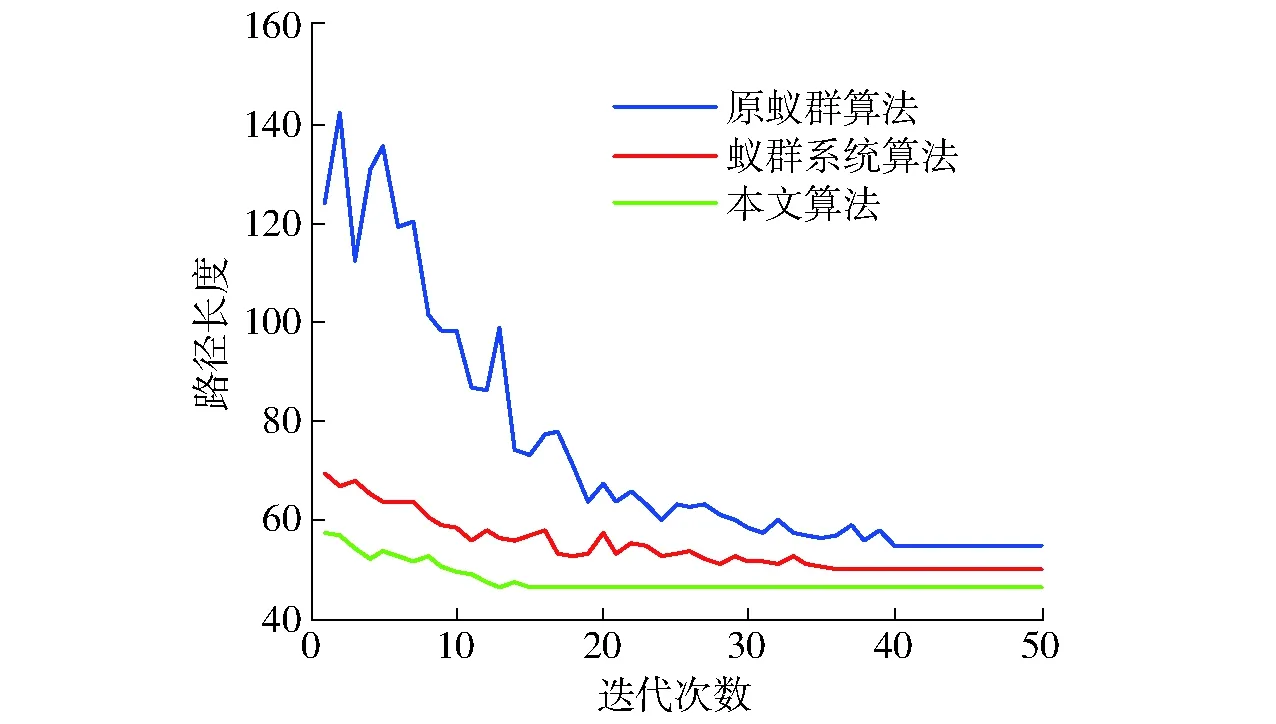
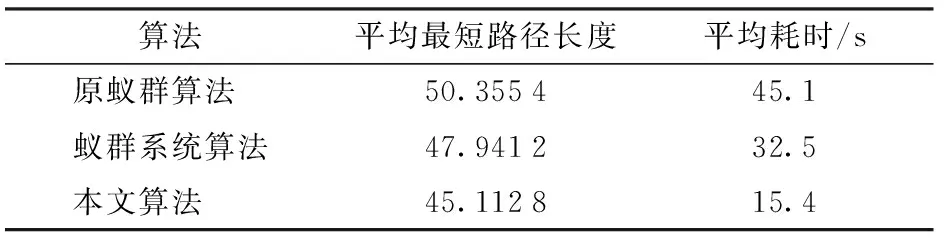
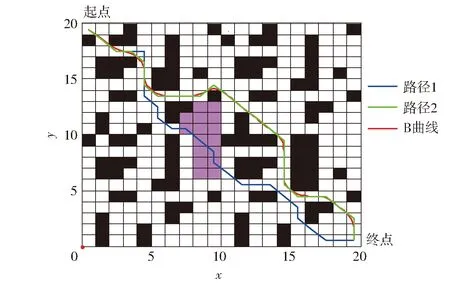
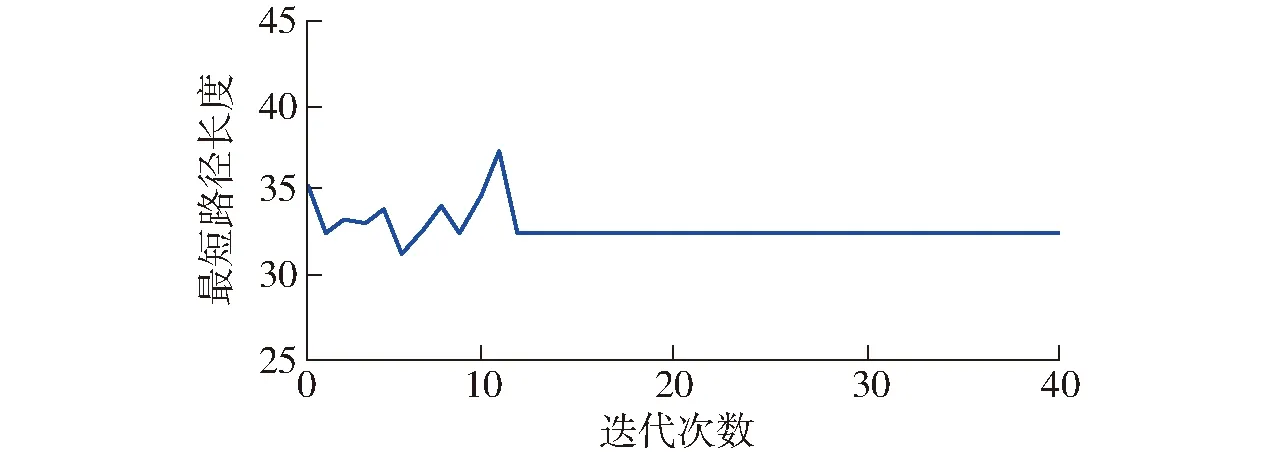
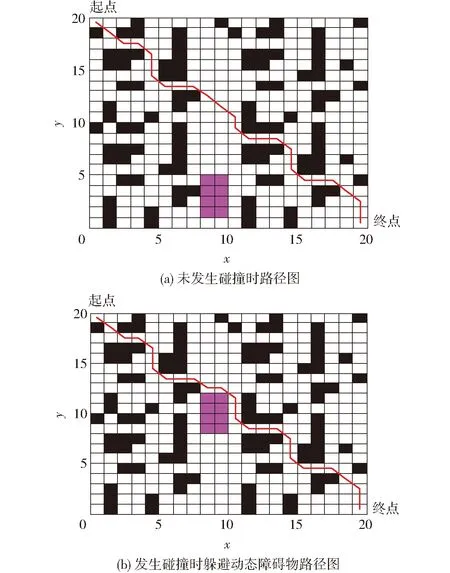
蚁群算法的参数配置将会直接影响其处理实际问题的能力[18-19]。在多策略A*蚁群算法中,有4个主要参数:q0为进化选择概率,即开发(广度)与探索(深度)间的调节概率,0 采用的2种环境地图如图1所示,其中,图1a为较大整块障碍物图,图1b为小块分散障碍物图,起点均为第1个栅格,终点均为第400 个栅格,蚂蚁数量m为30。停止条件为连续3次循环搜索中最优解的差异小于停止阈值。每组数据为5次试验数据的平均值。参数变化对路径的影响结果如图2和表1所示。 图1 环境地图Fig.1 Environmental maps 图2 参数对路径长度的影响Fig.2 Influence of parameters on path length 参数环境1环境2最短路径长度最长路径长度差值最短路径长度最长路径长度差值测试范围β28.627530.04171.414230.384930.97070.58581~15ρ28.627529.48110.853630.677831.36710.68930.1~0.9q028.627586.911858.284330.384994.254963.87000.1~1.0 参数选择是耗费时间的过程,因此希望能够降低任务的复杂性,选择能够对调节路线长度产生最大影响的主要参数。从表1中可以看出,参数q0的变化对产生路径长度影响最大。分析表明,q0是主要影响因子。因此,在闭环调节中只需选择参数q0进行调节。 2.2 参数的动态闭环调节 为提高蚁群算法在动态及复杂环境中的适应性,将改进的蚁群算法与经典闭环控制系统相结合,利用闭环反馈来动态调节改进蚁群算法中的参数q0,给出算法闭环控制框图如图3所示。 图3 算法闭环控制框图Fig.3 Algorithm framework of closed loop control 控制框架的核心在于反馈量的选取以及参数的调整策略。将本次迭代搜寻到的最短路径长度与前代最短路径长度差和前代长度的比值作为反馈量。当比值大于0时,说明本次搜索的路径区域解质量较差,需要加大搜索,应减小q0值,加大开发力度;相反,当比值小于0时,说明找到了更优路径,此区域具有探索价值,应加大探索力度,此时应增加q0值。而当比值为0时,需要对初次比值连续为1的次数进行计数并设定一个停滞门限,当累加计数超过此门限时,极有可能陷入局部极小。此时,应减小q0值,通过q0的调整而跳出极小区。具体的调整策略为 (6) 式中Nmax——停滞门限 num——种群出现连续停滞的代数累加ε——调整因子,0<ε<1 为得到全局最优解,q0不应超出其取值范围,应对q0的取值范围进行约束,0 路径规划是创建一个机器人从出发点到达目标点的免于碰撞的最优有序序列,为轨迹跟踪提供路线支持。因此,所规划的路径应满足平滑性的要求,尽量保证规划出的路径与实际运动路线相同。由于蚁群算法采用栅格表示环境地图,因此会在转弯处产生尖峰。 B样条曲线具有参数表达式简单、局部修改性、凸包性等优点,因此, B 样条曲线在工程设计中得到广泛应用[20]。由于三次B样条曲线在连接处二阶连续,将其用于路径规划时,速度和加速度都是连续的。因此,采用三次B样条来平滑蚁群已规划出的路径。 3.1 三次B样条曲线方程 一般,n次均匀B样条曲线的数学表达式为[17] (7) 其中 (8) 式中Pi——给定n+1个控制点Pi的坐标Fi,n(t)——n次B样条基函数 当n=3时,则有三次B样条曲线的基函数为 (9) 因此,三次B样条曲线方程为 (10) 用三次B样条曲线对尖峰路径进行光滑处理,图4为由9个控制点生成的光滑曲线。 图4 B样条曲线平滑结果Fig.4 Smooth result of B spline curve 3.2 三次B样条曲线平滑路径 三次B样条曲线对路径的平滑是在动态反馈A*蚁群算法得到最优路径后进行,也可称为路径的后处理环节,其流程如图5所示。 图5 B样条曲线的平滑流程Fig.5 Smoothing process of B spline curve 从4方面对本文算法的性能进行仿真分析:①A*蚁群与原蚁群算法仿真比较。②动态反馈A*蚁群算法整体性能与原蚁群算法、蚁群系统(ACS)[12]比较。③算法迭代过程中出现静态障碍物干扰的路径规划。④动态障碍物的路径规划。借助Matlab 2014a软件进行仿真,在2.3 GHz处理器、4 GB内存的Windows 10计算机上进行。 4.1 A*蚁群算法与原蚁群算法比较 对初始信息素优化的A*蚁群算法与原蚁群算法进行对比仿真。仿真初始条件设置如下:蚁群大小m=30,最大迭代次数NC-max=40,α=1,ρ=0.1,β=6,信息量常数Q=14;地图采用3.1节中的环境1。图6为原蚁群算法和A*蚁群算法路径图的对比结果。20次仿真的平均最短路线长度与迭代次数的关系的比较结果如图7所示。路径规划仿真20次比较的平均结果如表2所示。 图6 A*蚁群算法与原蚁群算法路径图Fig.6 Path planning of A* ant colony and original ant colony algorithms 图7 路径长度与迭代次数的关系Fig.7 Relationship between path length and number of iterations 由表2可以得出, A*蚁群算法通过优化初始信息素,从而加快原蚁群算法的收敛速度,减少迭代次数,规划出的最优路径质量要高于原蚁群算法,因此,提出的A*蚁群算法提高了原蚁群算法的实时性和规划效率。 4.2 动态反馈的A*蚁群算法与原蚁群算法、蚁群系统的比较 仿真初始条件如下:m=45,NC-max=50,α=1,ρ=0.1,β=6,q0=0.8,k=5,Q=14,在30×30的 表2 信息素初始化优化对比结果 栅格地图环境中进行测试,利用3种方法进行从起点到终点的路径规划,图8为本文提出的动态反馈的A*蚁群算法规划出的路径和采用B曲线平滑后的路径(采用三次B样条曲线)。图9为在迭代过程中主要控制参数q0的变化情况。 图8 动态反馈A*蚁群算法的平滑路径图Fig.8 Smooth path planning of A* ant colony algorithms optimization based on dynamic feedback 图9 q0变化曲线Fig.9 Variation curve of parameter q0 进行20次路径规划的仿真测试,得到3种算法的平均结果见图10和表3。 图10 路径长度与迭代次数的关系Fig.10 Relationship between path length and number of iterations 算法平均最短路径长度平均耗时/s原蚁群算法50.355445.1蚁群系统算法47.941232.5本文算法45.112815.4 从表3中可以看出,动态反馈的A*蚁群算法所规划出的路径长度平均值要优于原蚁群算法和蚁群系统算法所得的最优解,表明算法具有较好的稳定性且收敛速度较快,运行时间短。因此,本文算法具有较好的寻优能力和更快的收敛速度。该算法与原蚁群算法相比,平均可减少10.4%的路径成本和65.8%的计算时长。另外,与蚁群系统算法相比,平均可减少5.9%的路径成本和52.6%的计算时长。 4.3 静态障碍物干扰下的路径规划 图11 静态干扰下的路径规划图Fig.11 Path planning under static interference 在栅格地图中,初始条件设置如下:m=30,ρ=0.1,α=1,β=6,NC-max=40,q0=0.7。如图11所示,在第10次进化迭代后加入障碍物(在图11中用其它颜色标记),在第10代前规划得到路径1,在10代后加入静态障碍物得到路径2,红色曲线为B曲线平滑后的路径,采用三次B样条曲线。另外,路径长度与迭代次数的关系如图12所示。从图12可以看出,由于A*蚁群算法优化了初始信息素的设置,使路径初次搜索速度较快。在10次迭代后加入了静态障碍物,最优路径的长度也相应发生了波动,但由于闭环反馈参数调节参数q0,使算法快速收敛。由此可知,在路径搜索过程中,加入静态障碍物,能快速找到最优路径,具有较强的鲁棒性。 图12 路径长度变化曲线Fig.12 Path length variation curve 4.4 存在动态障碍物的路径规划 仿真初始条件设置如下:m=30,ρ=0.1,α=1,β=6,NC-max=40,q0=0.8。动态障碍物是矩形障碍物,沿y轴正向做速度为1栅格/s的匀速运动。图13a为未发生碰撞时的路径图,图13b为碰撞时躲避动态障碍物的路径图。可以看出,本文算法能躲避动态障碍物。 图13 存在动态障碍物的路径规划图Fig.13 Path planning under dynamic obstacles 蚁群算法作为一种基于生物习性的启发式进化方法,在移动机器人路径规划中的适用性和自进化能力需要得到进一步改善。因此,提出了一种基于动态反馈的A*蚁群算法。为进一步提升算法在搜索过程中的动态特性,将蚁群算法的优化目标作为反馈信息引入到蚁群算法中,将反馈信息经过处理后动态调节算法参数q0,通过q0的变化来控制3种策略进化的比例,以此来平衡算法的局部和全局搜索能力。同时,为加快运行效率,引入简化的A*算法来对初始信息素进行优化设置。其次,借助B样条曲线对已规划路径进行进一步平滑优化,以满足实际中移动机器人轨迹跟踪的要求。仿真结果表明,提出的规划算法与原蚁群算法和蚁群系统算法相比,具有更高的收敛速度和收敛质量。同时,在搜索过程中存在静态障碍物干扰和动态环境时,能够快速地规划出一条较优且平滑的路径,具有较好的适应性和鲁棒性。 1 朱大奇,颜明重. 移动机器人路径规划技术综述[J]. 控制与决策,2010, 25(7): 961-967. ZHU Daqi, YAN Mingzhong. Survey on technology of mobile robot path planning[J]. Control and Decision, 2010, 25(7): 961-967. (in Chinese) 2 ZHU Q, HU J, CAI W, et al. A new robot navigation algorithm for dynamic unknown environments based on dynamic path re-computation and an improved scout ant algorithm[J]. Applied Soft Computing, 2011, 11(8): 4667-4676. 3 韩永,刘国栋. 动态环境下基于人工势场的移动机器人运动规划[J]. 机器人,2006, 28(1): 45-49. HAN Yong, LIU Guodong. Mobile robot motion planning based on potential field in dynamic environment[J]. Robot, 2006, 28(1): 45-49. (in Chinese) 4 MANIKAS W, ASHENVVI K, WAINWRIGHT R. Genetic algorithms for autonomous robot navigation[J]. IEEE Instrumentation & Measurement Magazine, 2008, 10(6): 26-31. 5 NI B, CHEN X. New approach of neural network for robot path planning[C]∥2004 IEEE International Conference on Systems, Man and Cybernetics, 2004: 735-739. 6 吴宪祥,郭宝龙,王娟. 基于粒子群三次样条优化的移动机器人路径规划算法[J]. 机器人,2009, 31(6): 556-560. WU Xianxiang, GUO Baolong, WANG Juan. Mobile robot path planning algorithm based on particle swarm optimization of cubic splines[J]. Robot, 2009, 31(6): 556-560. (in Chinese) 7 GARRO B A, SOSSA H, VAZQUEZ R A. Evolving ant colony system for optimizing path planning in mobile robots[C]∥ IEEE Electronics, Robotics and Automotive Mechanics Conference, 2007: 444-449. 8 WANG Y, YANG Y, YUAN X, et al. Autonomous mobile robot navigation system designed in dynamic environment based on transferable belief model[J]. Measurement, 2011, 44(8): 1389-1405. 9 刘建华,杨建国,刘华平,等. 基于势场蚁群算法的移动机器人全局路径规划方法[J/OL]. 农业机械学报,2015, 46(9): 18-27. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150903&flag=1.DOI:10.6041/j.issn.1000-1298.2015.09.003. LIU Jianhua, YANG Jianguo, LIU Huaping, et al. Robot global path planning based on ant colony optimization with artificial potential field[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9): 18-27. (in Chinese) 10 王沛栋,冯祖洪,黄新. 一种改进的机器人路径规划蚁群算法[J]. 机器人,2008, 30(6): 554-560. WANG Peidong, FENG Zuhong, HUANG Xin. An improved ant colony algorithm for mobile robot path planning[J]. Robot, 2008, 30(6): 554-560. (in Chinese) 11 赵娟平,高宪文,符秀辉,等. 移动机器人路径规划的改进蚁群优化算法[J]. 控制理论与应用,2011, 28(4): 457-461. ZHAO Juanping, GAO Xianwen, FU Xiuhui, et al. Improved ant colony algorithm of path planning for mobile robot[J]. Control Theory & Application, 2011, 28(4): 457-461. (in Chinese) 12 DORIGO M, GAMBARDELLA L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 53-66. 13 郭宗环, 谢志江, 宋代平,等. 基于改进蚁群算法的风洞试验俯仰机构运动误差优化[J/OL]. 农业机械学报, 2016, 47(7):375-381. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160751&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.07.051. GUO Zonghuan, XIE Zhijiang, SONG Daiping, et al. Error optimization of pitching mechanism motion in wind tunnel test based on improved ant colony algorithm[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2016,47(7):375-381. (in Chinese) 14 吴小勇, 谢志江, 宋代平,等. 基于改进蚁群算法的3-PPR并联机构位置正解研究[J/OL]. 农业机械学报, 2015, 46(7):339-344. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150748&flag=1.DOI:10.6041/j.issn.1000-1298.2015.07.048. WU Xiaoyong, XIE Zhijiang, SONG Daiping, et al. Forward kinematics of 3-PPR parallel mechanism based on improved ant colony algorithm[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2015,46(7): 339-344. (in Chinese) 15 王殿君. 基于改进A*算法的室内移动机器人路径规划[J]. 清华大学学报:自然科学版,2012, 52(8): 1085-1089. WANG Dianjun. Indoor mobile-robot path planning based on an improved A*algorithm[J]. Journal of Tsinghua University: Science and Technology, 2012, 52(8): 1085-1089. (in Chinese)16 顾青,豆风铅,马飞. 基于改进A*算法的电动车能耗最优路径规划[J/OL]. 农业机械学报,2015, 46(12): 316-322.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20151243&flag=1.DOI:10.6041/j.issn.1000- 1298.2015.12.043. GU Qing, DOU Fengqian, MA Fei. Energy optimal path planning of electric vehicle based on improved A*algorithm[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12): 316-322. (in Chinese) 17 马飞, 杨皞屾, 顾青,等. 基于改进A*算法的地下无人铲运机导航路径规划[J/OL]. 农业机械学报, 2015, 46(7):303-309. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150743&flag=1.DOI:10.6041/jissn.1000-1298.2015.07.043. MA Fei, YANG Haoshen, GU Qing, et al. Navigation path planning of unmanned underground LHD based on improved A*algorithm[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(7): 303-309. (in Chinese) 18 杜鹏桢,唐振民,孙研. 一种面向对象的多角色蚁群算法及其TSP问题求解[J]. 控制与决策,2014(10): 1729-1736. DU Pengzhen, TANG Zhenmin, SUN Yan. An object-oriented multi-role ant colony optimization algorithm for solving TSP problem[J]. Control and Decision, 2014(10): 1729-1736. (in Chinese) 19 史恩秀,陈敏敏,李俊,等. 基于蚁群算法的移动机器人全局路径规划方法研究[J/OL]. 农业机械学报,2014, 45(6):53-57. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20140609&flag=1.DOI:10.6041/j.issn.1000-1298.2014.06.009. SHI Enxiu, CHEN Minmin, LI Jun, et al. Research on method of global path-planning for mobile robot based on ant-colony algorithm[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(6): 53-57. (in Chinese) 20 赵彤,吕强,张辉,等. 三次均匀B样条曲线高速实时插补研究[J]. 计算机集成制造系统,2008, 14(9): 1830-1836. ZHAO Tong, LÜ Qiang, ZHANG Hui, et al. High-speed real-time interpolation of cubic uniform B-spline curve[J]. Computer Integrated Manufacturing Systems, 2008, 14(9): 1830-1836. (in Chinese) Smooth Path Planning Method Based on Dynamic Feedback A*Ant Colony Algorithm HUANG Chen1FEI Jiyou1,2LIU Yang3LI Hua2LIU Xiaodong2 (1.CollegeofMechanicalEngineering,DalianJiaotongUniversity,Dalian116028,China2.CollegeofBulletTrainApplicationandMaintenanceEngineering,DalianJiaotongUniversity,Dalian116028,China3.CollegeofEngineering,PukyongNationalUniversity,Pusan608737,Korea) A smooth path planning method for mobile robot with A*ant colony optimization was proposed based on dynamic feedback for mobile robot. First of all, in order to overcome the disadvantage about slow convergence speed of ant colony algorithm, simplified A*algorithm was presented to optimize the initial pheromone settings, which was able to solve the blindness of the first search. In this step, the planning path with the minimum value of the valuation function was obtained by the evaluation function of A*algorithm. And the presented multi-evolutionary strategy mechanism which could increase search space was used to strengthen the global search ability of the algorithm. Secondly, in order to further improve the adaptability of algorithm about the problem of local minimum and stagnation in the path planning, the key parameters of the algorithm were systematically analyzed and the closed-loop feedback idea was adopted to adjust the parameters of ant colony optimization algorithm dynamically. Finally, combining with the cubic B spline curve method, the planning path was smoothed to meet the practical movement route of mobile robot. The simulation experiment results showed that compared with traditional ant colony (AC), A*ant colony optimization based on dynamic feedback could reduce 10.4% of the average path cost and shorten 65.8% of the computing time in average. In addition, compared with ant colony system (ACS), the average path cost could be reduced by 5.9%, the calculation time could be shortened by 52.6%. The improved ant colony optimization algorithm could plan a smooth and high quality path in both the dynamic and static environments. path planning; ant colony algorithm; dynamic feedback; A*algorithm; B spline curve 10.6041/j.issn.1000-1298.2017.04.004 2016-07-19 2016-08-30 国家自然科学基金项目(51376028)和“十二五”国家科技支撑计划项目(2015BAF20B02) 黄辰(1982—),女,工程师,博士生,主要从事运动控制研究,E-mail: huangchen054@163.com 费继友(1964—),男,教授,博士生导师,主要从事现代测试技术研究,E-mail: fjy@djtu.edu.cn TP391.41 A 1000-1298(2017)04-0034-07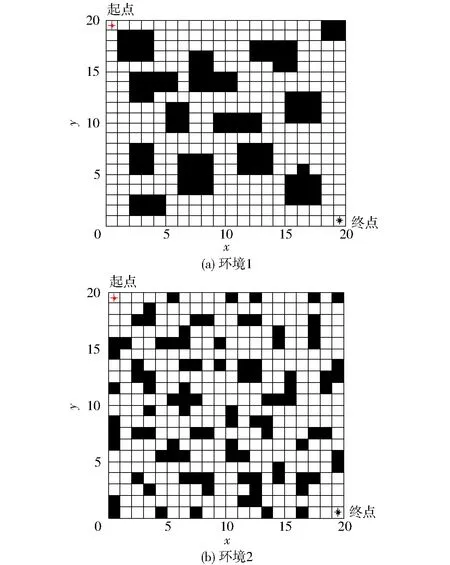

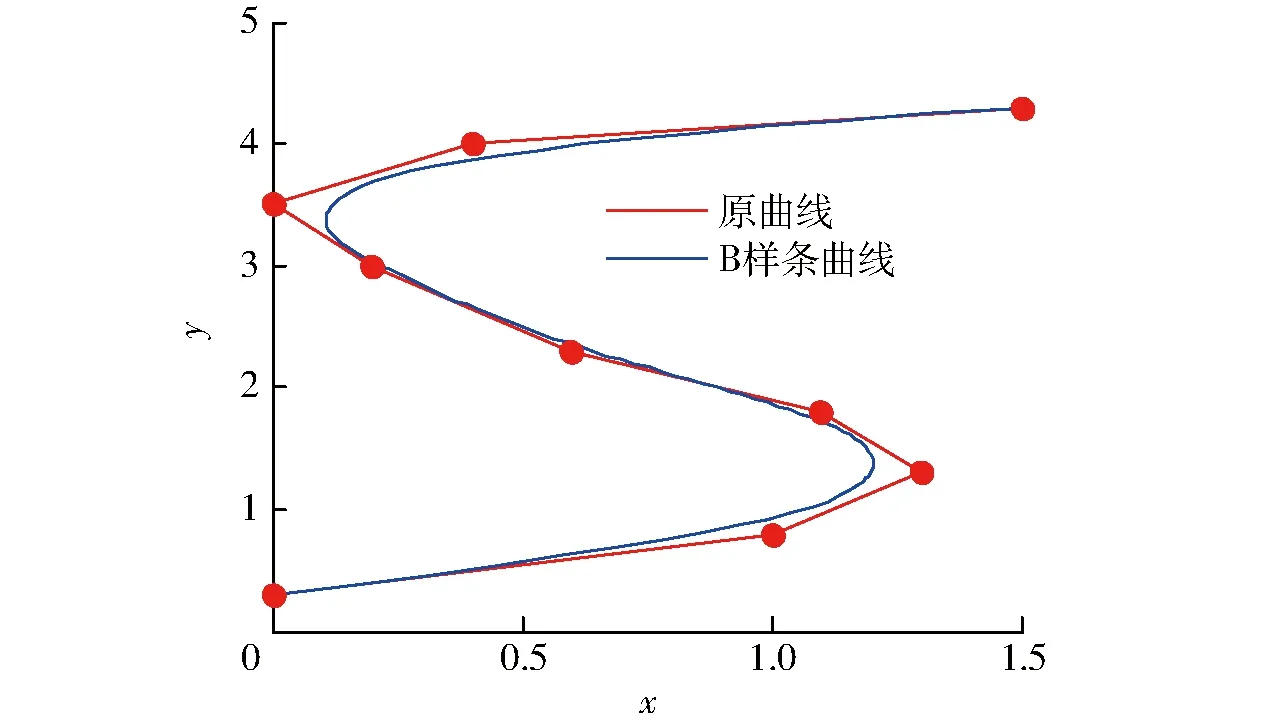
3 三次B样条曲线平滑路径
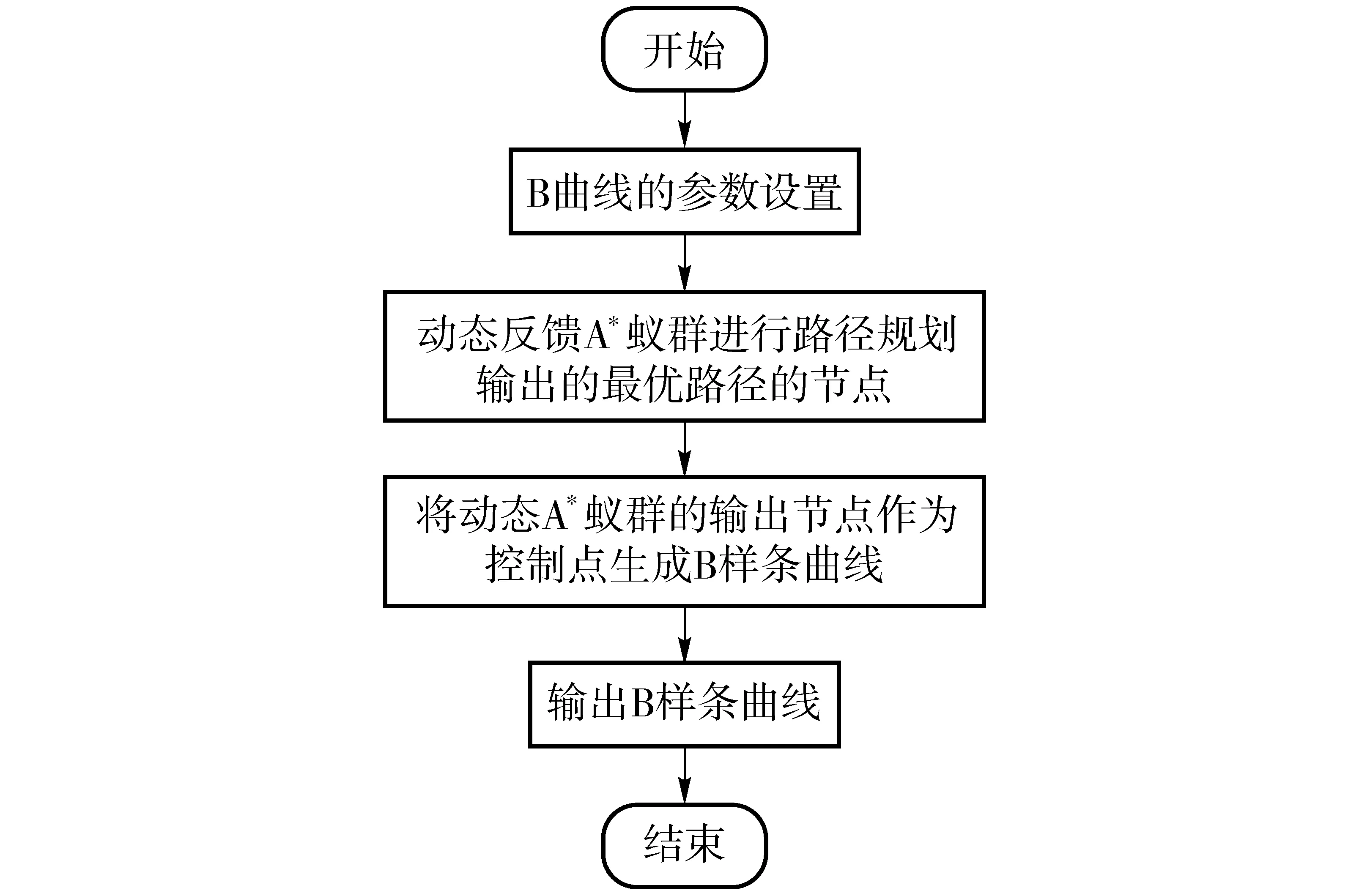
4 仿真
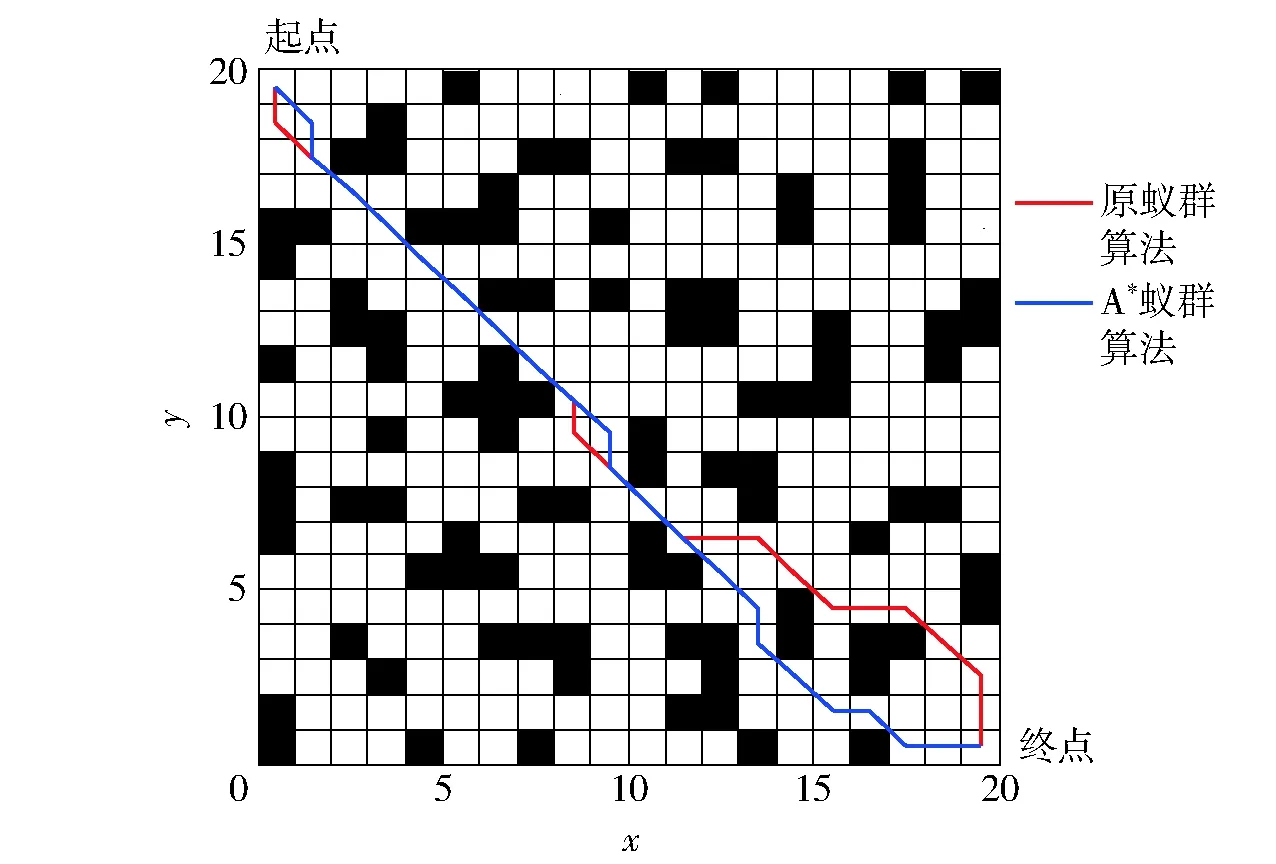
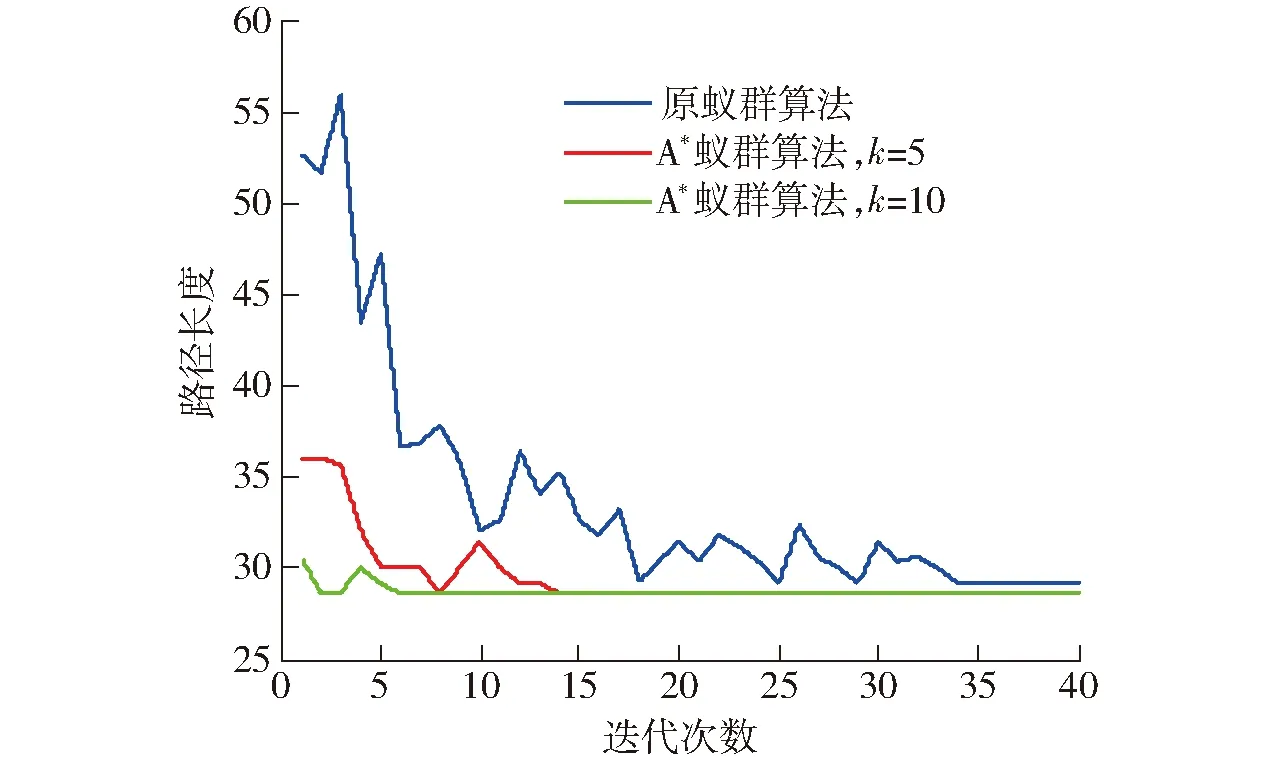
5 结束语
