一种无证书签名方案的分析与改进

史华婷，万中美

(河海大学 理学院,江苏 南京 211100)

一种无证书签名方案的分析与改进

史华婷，万中美

(河海大学 理学院,江苏 南京 211100)

无证书公钥密码体制虽然解决了基于身份密码体制中的密钥托管问题,但是当随机预言模型被具体的哈希函数实例化时,将会导致无证书签名方案在现实生活中的不安全。标准模型下的证明为无证书签名方案提供充分的保障。通过两种具体的攻击方法,对李艳琼提出的标准模型下的无证书签名方案进行安全性分析,指出其不能抵抗公钥替换攻击和恶意的KGC攻击。针对存在的安全问题,对原来的无证书签名方案进行改进,并加强方案与公钥、私钥等参数的联系,从而达到安全要求。在标准模型下,基于NGBDH问题和Many-DH问题的困难性假设,改进的无证书签名方案在自适应选择消息攻击下是存在性不可伪造的。与李艳琼提出的方案相比,改进后的无证书签名方案在安全性上有了更高的优势。

无证书签名；标准模型；NGBDH问题；Many-DH问题

0 引 言

为了解决基于身份密码体制[1]中的密钥托管问题,Al-Riyami和Paterson[2]在2003年亚密会议上引入了无证书公钥密码体制的概念。无证书公钥密码体制区别于基于身份密码体制,它需要一个可信密钥生成中心(Key Generation Center,KGC),负责生成用户的部分私钥。在无证书公钥密码体制中,私钥不是由KGC单独生成的,需要用户随机选择一个秘密值和部分私钥组合,才能生成完整的私钥,这就克服了密钥托管问题。

Yum和Lee[3]在2004年提出了一个由两种属性构建的无证书签名的通用结构。但是,Hu和Wong[4]发现该方案是不安全的,其不能抵抗第一类公钥替换攻击,并对其进行了改进。为了提高计算效率,Zhang等[5]提出了一种安全的无证书签名方案。文献[6]给出了一类无证书签名方案的构造方法,并对其进行安全性证明。文献[7]提出了一种高效的签名方案,但是文献[8]发现其是不安全的,并提出了改进方案。文献[9]对文献[8]在安全性和效率上存在的不足进行改进,提出了不使用双线性对的签名方案。

文献[10]指出，随机预言模型下的可证安全并不是严格意义上的安全,标准模型可以保持随机预言模型中的安全特性。基于以上问题,Liu等[11]在2007年亚密会议上提出了第一个标准模型下的无证书签名方案。随后,Xiong[12]、Yu[13]等又对Liu等[11]的提出方案进行改进。文献[14]提出了一种标准模型下的无证书短签名方案,并进行了安全性分析。李艳琼[15]根据文献[16]构造了一种新的无证书签名方案,但是它不能抵抗两类攻击。

针对李艳琼的方案进行了安全分析,给出了两种具体的攻击方法,指出其不能抵抗公钥替换攻击和恶意的KGC攻击,并提出了一种改进的无证书签名方案。基于NGBDH问题和Many-DH问题的困难性假设,证明改进方案在标准模型下是存在性不可伪造的。

1 预备知识

1.1 双线性映射

设G1是由g产生的阶为素数q的乘法循环群,G2为同阶乘法循环群。双线性映射e:G1×G1→G2,满足以下条件：

(2)非退化性：e(g,g)≠1。

(3)可计算性：存在有效的算法计算e。

1.2 困难性问题

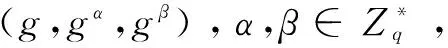
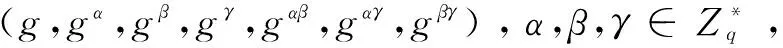
设算法C解决G上的Many-DH问题的概率ε为：

Pr[A(g,gα,gβ,gγ,gαβ,gαγ,gβγ)=gαβγ]≥ε

2 李艳琼方案的安全性分析

2.1 攻击1

对方案实施如下恶意的KGC攻击：

(2)窃听在公钥pkID*下身份ID*对消息m的签名σ=(V,Ru,Rm),在相同公钥下KGC生成身份ID*对任意m*的有效签名。

因为满足：

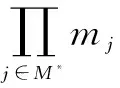
所以伪造的签名σ*=(V*,Ru*,Rm*)是有效的,即该方案不能抵抗恶意的KGC攻击。

2.2 攻击2

敌手AI用新公钥伪造用户ID*的签名：

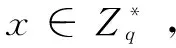
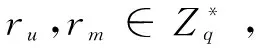
显然,伪造的签名σ*满足验证算法,所以该方案不能抵抗公钥替换攻击。

3 新的无证书签名方案

1)系统参数设置算法：给定安全参数k,KGC执行以下步骤：

(1)随机选择两个阶为素数q的乘法循环群G1、G2,g为G1的生成元。存在一个双线性映射e:G1×G1→G2。

(4)取G1中的点Q,定义函数f(Q),如果Q的x坐标为奇数,则f(Q)=1；否则,f(Q)=0。

系统的公开参数为params={G1,G2,e,g,g1,g2,u',m0,m1,v,U,H0,H,f}。

6)验证算法：验证者使用params和pkID对(m,σ)进行验证：

(1)验证e(pkID,1,pkID,2)=e(g1,v)；若不成立,则终止。

(2)计算b=f(Ru),h=H(m,ID,pkID,2,Ru,Rm,mb,v)。

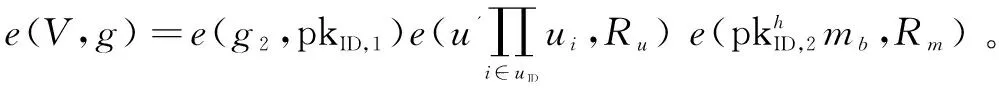
4 安全模型

无证书签名方案的敌手模型与文献[15]中的类似,第一类敌手AI作为第三方攻击者,可以替换任意用户的公钥,但不知道主密钥和部分私钥。第二类敌手AII作为一个恶意的KGC,知道主密钥,但不可以替换用户的公钥。

下面通过两种游戏定义无证书签名方案的安全模型。

4.1 游戏1

敌手AI和挑战者C之间的游戏如下：

1)系统参数设置：输入安全参数k,KGC生成params和msk。C将params发送给AI,msk保密。

2)询问：AI进行如下询问:

(1)部分私钥询问：C接收到AI对身份ID的部分私钥的询问,返回pskID给AI。

(2)公钥询问：AI询问身份ID的pkID,C返回pkID给AI。

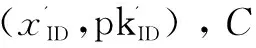
(4)私钥询问：C接收到AI对身份ID的私钥询问,返回skID给AI。

(5)签名询问：AI可以询问身份为ID的用户对任意消息m的签名,C返回签名给AI。

3)伪造：AI输出身份为ID*的用户对消息m*的签名σ*。如果AI满足以下条件且Verify(params,ID*,pkID*,m*,σ*)=1,那么AI就赢得了游戏：

(1)AI没有发出对ID*的部分私钥询问。

(2)AI没有发出对ID*的私钥询问。

(3)AI没有发出对(ID*,m*)的签名询问。

那么,AI成功的概率定义为AI赢得游戏1的概率。

4.2 游戏2

敌手AII和挑战者C之间的游戏如下：

1)系统参数设置：输入安全参数k,KGC生成params和msk,并将params、msk发送给AII。

2)询问：AII发出和游戏1相同的私钥询问、公钥询问、公钥替换询问和签名询问。

3)伪造：AII输出身份为ID*的用户对消息m*的签名σ*。如果AII满足以下条件且Verify(params,ID*,pkID*,m*,σ*)=1,那么AII就赢得了游戏。

(1)AII没有询问过身份ID*的私钥。

(2)AII没有替换身份ID*的公钥。

(3)AII没有询问过身份ID*对消息m*的签名。

那么,AII成功的概率定义为AII赢得游戏2的概率。

定义3：如果上述两类敌手都能以不可忽略的优势赢得游戏，那么就称无证书签名方案在适应性选择消息攻击下是存在性不可伪造的。

5 安全证明

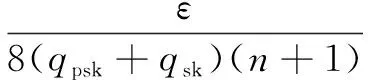
证明：输入(g,gα,gβ),计算(gαβγ,gγ),利用算法C解决NGBDH问题。C包含了初始为空的列表L={ID,pskID,xID,pkID,skID}。

2)询问：在询问阶段，算法C回复AI的一系列询问。

(1)部分私钥询问：AI询问身份ID的pskID,C检查列表L,若存在,直接返回pskID给敌手AI。若不存在,C检查Ju(u)=0modq：若Ju(u)=0modq,C终止模拟；若Ju(u)≠0modq,C随机选取r∈Zq,计算部分私钥：

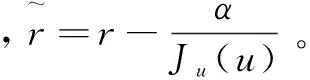
C返回pskID给AI,并将元组添加到L。

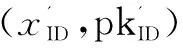
(4)私钥询问：C接收到AI发出的对身份ID的私钥询问,检查列表L。若存在,直接返回skID给敌手AI；若不存在,检查Ju(u)=0modq。如果Ju(u)=0modq,C终止模拟；否则,C发出部分私钥询问获得身份ID的pskID,运行用户密钥生成算法获取(xID,pkID),运行私钥生成算法获得skID。C返回元组给AI并添加到L。

(5)签名询问：AI询问消息m的签名,C执行以下步骤：

若Ju(u)≠0modq,C检查L,若存在(pkID，skID),则C运行签名算法生成消息m的签名σ,并返回给AI。

否则,C选择r1∈Zq,使f(gr1)=1(如果f(gr1)=0,C再选r1∈Zq,使f(gr1)=1)。随后,C随机选择rm∈Zq,按如下生成σ=(V,Ru,Rm)：

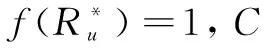
4)概率计算：算法C在模拟过程中没有终止,必须满足以下条件：

(1)部分私钥询问满足Ju(u)≠0modq。

(2)所有的私钥询问满足Ju(u)≠0modq。

定义3个事件A*,B*,Ai：

A*：Ju(u*)=0modq；

Ai：Ju(ui)≠0modl,i=1,2,…,qI。

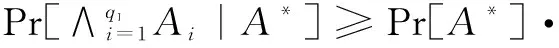
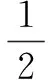
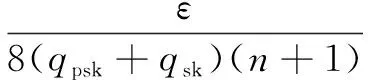
证明：输入(g,gα,gβ,gγ,gαβ,gαγ,gβγ),计算gαβγ。利用算法C解决Many-DH问题,C包含了一个初始为空的列表L={ID,xID,pkID,skID}。

2)询问阶段：AII发出以下询问。

(1)公钥询问：AII询问身份ID的公钥,C检查列表L。若存在,直接返回pkID给敌手AII。若不存在,C随机选取xID∈Zq,计算pkID=(pkID,1,pkID,2)=(gαγxID,g)作为身份ID的公钥。C返回pkID给AII,并将元组添加到L。

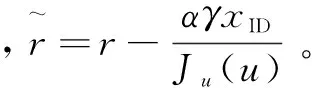
C返回skID给AII,并将元组添加到L。

(4)签名询问：AII询问消息m的签名,C执行以下步骤：

若Ju(u)≠0modq,C检查L,若(pkID,skID)存在,则C运行签名算法生成消息m的签名σ,并返回给AII。否则,C随机选择r1∈Zq,使f(gr1)=1(如果f(gr1)=0,C再选r1∈Zq,使f(gr1)=1)。随后,C随机选择rm∈Zq,按如下生成σ=(V,Ru,Rm)：

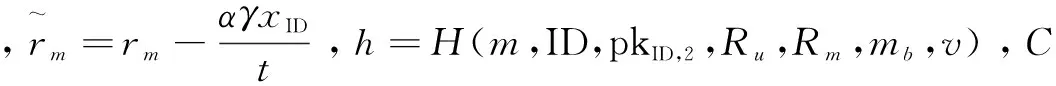
6 结束语

通过具体的攻击方法,对李艳琼的方案进行了安全性分析,指出其不能抵抗公钥替换攻击和恶意的KGC攻击。为此，提出了一种改进的无证书签名方案,克服了原方案的安全缺陷。基于NGBDH问题和Many-DH问题，在标准模型下证明了改进方案的安全性。与原方案相比，改进方案增强了与公钥、私钥等参数的联系，具有更强的安全性。在今后的研究中,构造安全高效的标准模型下的无证书签名方案仍是研究的重点。

[1]ShamirA.Identity-basedcryptosystemsandsignatureschemes[C]//ProceedingsoftheCrypto’84.[s.l.]:[s.n.],1984:47-53.

[2]Al-RiyamiSS,PatersonKG.Certificatelesspublickeycryptography[C]//ProceedingsoftheAsiacrypt’2003.[s.l.]:[s.n.],2003:452-473.

[3]YumDH,LeePJ.Genericconstructionofcertificatelessencryption[C]//ProceedingsoftheACISP’2004.[s.l.]:[s.n.],2004:802-811.

[4] Hu B C,Wong D S,Zhang Z,et al.Key replacement attack against a generic construction of certificateless signature[C]//Lecture notes in computer science.[s.l.]:[s.n.],2006:235-246.

[5] Zhang Z,Wong D,Xu J,et al.Certificateless public key signature:security model and efficient construction[C]//Lecture notes in computer science.[s.l.]:[s.n.],2006:293-308.

[6] 张 磊,张福泰.一类无证书签名方案的构造方法[J].计算机学报,2009,32(5):940-945.

[7] 李凤银,刘培玉,朱振方.高效的无证书签名方案[J].计算机工程与应用,2011,47(10):23-26.

[8] 刘 倩,范安东,张丽娜,等.一个高效的无证书签名方案分析与改进[J].河南科技大学学报:自然科学版,2014,35(4):49-53.

[9] 刘二根,周华静,王 霞,等.一个安全高效的无证书签名方案的分析与改进[J].华东交通大学学报,2015,32(4):105-109.

[10] 冯登国.可证明安全性理论与方法研究[J].软件学报,2005,16(10):1743-1756.

[11] Liu J K,Au M H,Susilo W.Self-generated-certificate public key cryptography and certificateless signature/encryption scheme in the standard model:extended abstract[C]//Proceedings of the ASIACCS’2007.New York:ACM Press,2007:273-283.

[12] Xiong H,Qin Z G,Li F G.An improved certificateless signature scheme secure in the standard model[J].Fundamenta Informaticae,2008,88(1-2):193-206.

[13] Yu Y,Mu Y,Wang G,et al.Improved certificateless signature scheme provably secure in the standard model[J].IET Information Security,2012,6(2):102-110.

[14] 魏春艳,蔡晓秋.标准模型下的高效无证书短签名方案[J].计算机工程,2012,38(13):119-121.

[15] 李艳琼,李继国,张亦辰.标准模型下安全的无证书签名方案[J].通信学报,2015,36(4):185-194.

[16] 李继国,姜平进.标准模型下可证安全的基于身份的高效的签名方案[J].计算机学报,2009,32(11):2130-2136.

Analysis and Improvement of a Certificateless Signature Scheme

SHI Hua-ting，WAN Zhong-mei

(College of Science,Hohai University,Nanjing 211100,China)

Although certificateless cryptography solves the key escrow problem in the identity-based public cryptography,a CLS scheme may not be secure in the real world when the random oracles are instantiated by concrete hash functions.The security of certificateless signature scheme can be proved adequately in the standard model.Security analysis has been carried out for Li Yanqiong’s CLS scheme by detailed method attack,whose results show that the scheme is not secure against key replacement attacks and malicious KGC attack.In view of the existing secure problems,an improved certificateless signature scheme has been proposed,which enhances the contact with the public key,private key and other parameters,to achieve the safety requirements.Based on the NGBDH problem and Many-DH problem in the standard model,an improved CLS scheme is proved secure against existentially under adaptive chosen message attack.Compared with Li Yanqiong’s scheme,the improved CLS scheme has higher advantages in the security.

certificateless signature;standard model;NGBDH problem;Many-DH problem

2016-05-24

2016-09-08 网络出版时间：2017-03-07

国家自然科学基金资助项目(61103183)

史华婷(1991-),女,硕士,研究方向为密码学理论与技术;万中美,副教授,硕士生导师,研究方向为信息安全、密码学理论与技术。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170307.0921.048.html

TP309

A

1673-629X(2017)05-0133-05

10.3969/j.issn.1673-629X.2017.05.028