数据挖掘中描述性数据汇总技术在中小学教学质量分析中的应用
2017-06-05孙庆
孙庆
(上海市黄浦区教育信息中心,上海200011)
数据挖掘中描述性数据汇总技术在中小学教学质量分析中的应用
孙庆
(上海市黄浦区教育信息中心,上海200011)
本文重点阐述了在基于学科考试的中小学教学质量分析过程中,如何利用数据挖掘过程中的描述性数据汇总技术,对考试分数实施汇总分析,展现考试分数的数据特征,识别考试分数中的噪声数据,进而为有效开展学科教学质量的测评分析提供科学依据。
教学质量分析;数据挖掘;数据预处理;描述性数据汇总
一、引言
为了全面提高中小学学科教学质量,有效地指导学校开展学科教学活动,区(县)基础教育管理部门往往需要通过开展区域性的学科统考,并对考试成绩实施全样本数据统计分析,从中获取基于不同层面的学科教学质量的反馈信息,并据此对区域内学校的学科教学实施有效的监测和指导。因此,构建以成绩统计分析为基础的中小学教学质量分析系统,成了区(县)基础教育管理部门较为关注的一项信息化建设工作。
然而,对于教学质量分析系统来讲,其上层应用特色应体现在,能够针对区内学校的学科教学质量及学生学业发展水平,为区教育管理部门提供全面、准确、综合的评估分析报告。进而为区教育管理部门,对全区学校的学科教学质量实施有效监控,提供科学的辅助决策依据。但是,要达到上述之目的,构建的教育质量分析系统就必须具备能够分析、呈现考试成绩的总体数据特征,以及辨识、去除隐藏于考试成绩中的噪声数据的功能。而这些功能,正是对数据挖掘在预处理过程中所利用的描述性汇总技术的具体实现。
二、数据挖掘相关技术
1.数据挖掘
数据挖掘(DM,Data Mining)就是从常态生成的、带有噪声的、大容量的真实业务数据中,寻找并获取隐藏其内的新的知识和信息的过程。这个过程对驻留在数据库中的已有的大量数据,实施了抽取、转换、分析及模型化处理,并最终为实际业务的开展生成提供了具有辅助决策支持作用的关键性数据。数据挖掘的过程,有效地实现了对原有业务数据的进一步的深度应用。数据挖掘经常被称为另一个常用的术语:数据库中的知识发现(KDD,Knowledge Discovery in Databases)。通常知识发现的过程由以下步骤组成:数据清理、数据集成、数据选择、数据变换、数据挖掘、模式评估和知识表示。
2.数据预处理
由于真实的业务数据存在着缺陷,带有噪声且不甚完整。如果对这类品质不高的数据急于实施数据挖掘,必然会影响最终的数据挖掘结果。然而,通过数据预处理则可以有效地改善数据的质量,以使后续实施的数据挖掘过程,能够在性能和精度上得到尽可能大地提高。利用数据预处理技术可以先期检测到各类异常数据,从而为调整改善数据质量和规范约束待分析数据,创造了有利条件。数据预处理为最后获得高质量的知识发现,提供了重要的基础保障。由此可以看到,数据预处理的重要作用体现在,它为改善现实数据的质量和获取高质量的数据挖掘结果,奠定必要的基础。所以,数据预处理是知识发现过程中不可或缺的重要环节,它由数据清理、数据集成、数据变换和数据规约等几个步骤构成。
3.描述性数据汇总
全面了解数据的整体特征,是成功实施数据预处理的必要前提。那么如何才能准确有效地获取数据的整体特征,并充分展示出数据集的集中趋势和离散趋势呢?对这个问题的回答是:必须利用描述性数据汇总技术。描述性数据汇总技术主要是基于一批描述性统计度量,对数据实施计算分析,识别出数据的固有特性,暴露出潜藏在数据中的噪声点或离群点。这批统计度量由两类组成,其中一类是用于描述数据集中趋势的度量:中位数(median)、众数(mode)和平均值(mean)。而另一类是用于描述数据离散趋势的度量:标准差(σ)、四分位数(quartiles)和四分位极差(IQR)。
三、考试分数的描述性数据汇总分析
1.度量考试分数的集中趋势特征
在描述性数据汇总中,用以考察度量数据集中趋势的方法常见的有三种,它们分别是分布式度量(distributive measure)、代数度量(algebraicmeasure)和整体度量(holistic measure)。其中,分布式度量是指,把数据集分割成更小的数据子集,然后计算出每个子集的度量值,最后将计算结果进行合并以得到整个数据集度量值的度量。代数度量是指,由包含了一个或多个分布式度量的代数函数所计算的度量。而整体度量是指,对整个数据集计算的度量。
在中小学教学质量分析中,当导入一次考试的所有学生的原始考分后,是通过计算平均分、众数和中位数这三个集中量数来获取这批原始考分的集中趋势信息的。然而,平均分、众数和中位数正是属于描述性数据汇总技术中的集中趋势度量。其中,平均数属于代数度量,因为它可以通过分布式度量sum()/count()计算得到,而中位数和众数都是属于整体度量。如果是区(县)级的学科质量测评考试,依据平均分、众数和中位数这三个集中量数就可以对区内不同学校之间的学科教学质量进行比较;如果是校级的学科质量测评考试,则可以对校内不同班级之间的学科质量进行比较。因为平均分、众数和中位数能够很好地归纳出,基于不同层面(学校、班级)的考生群体的总体考核情况。
(1)平均分(mean)
平均数就是指一组数据值的均值,它是考察和度量数据集中趋势最有效、最常用的数据度量值。在教育质量分析中,我们称之为平均分,也就是指考试原始分数的算术平均数:

其中,Xi代表第i个考生的原始考分,n代表参加考试的考生总人数。平均分容易计算、易于理解,并具有较强的代表性。但是,平均分的主要问题是对于极端值表现得比较敏感,容易受到极端数值的影响而致使其丧失代表性。例如,某次考试很可能因为少数几个非常低的分数而拉低了整个考试的平均分。因此,为了消除少数极端数据值对平均分的影响,我们可以去除数据集合高、低两端的极端数值,然后再计算出能够更加准确地体现集中趋势的均值。例如,在计算考试平均分时,我们可以考虑去掉原始考分中,高、低两端一定比例的数据值,使计算得到的平均分能够更为准确地描述出原始考分的集中趋势,从而为反映考生群体的总体水平提供有效的度量信息。当然,被去除数据的比例值需谨慎确定,如果比例太大反而会适得其反,影响平均分的有效性。
(2)中位数(median)
就考试而言,中位数是指在全样本空间内,将全部考生的原始成绩按序排列,若考生人数为单数,就取正中间的那一个分数作为考试成绩的中位数;若考生人数为双数,则取中间两个分数的平均数作为考试成绩的中位数。相比于平均分,中位数的优势在于,其度量值不受极端数值影响。当遇到平均分受到极端考分影响而失去代表性时,就可以用中位数的大小来代表这次考试分数。中位数属于整体度量,其缺点在于不够灵敏,且没有平均分可靠。
当然,中位数还可以通过划分数据区间的方法(或称分组)来计算获取,具体的计算方法是:按照指定的组距(即数据区间宽度)将数据集划分成若干个连续的数据区间,然后确定每个区间内的数据个数(即,区间频率)。例如,可以按照10分的区段间隔,将原始考分划分入0~10,10~20,20~30等区间,然后清点每个区间内原始考分的个数。我们把包含中位数的那个区间称为中位数区间,而中位数就可以按照下面这个公式计算获取:
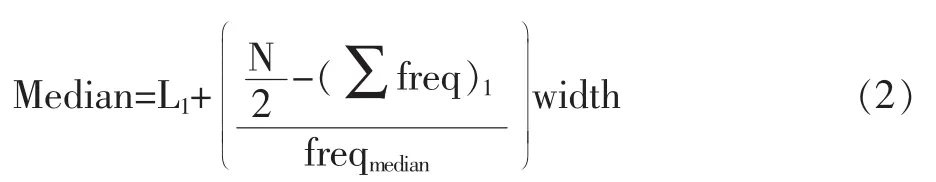
其中,Ll是中位数所在区间的下限,N是整个数据集的数据个数,(∑freq)l是低于中位数所在区间的其它所有区间的频率总和,freqmedian是中位数所在区间的频率,width是数据区间的宽度。当然,这样计算得到的只能是数据集中位数的近似值。
(3)众数(mode)
在数据集合中,出现次数最多的那个数被称为众数。就考试而言,众数就是考试成绩样本空间中,出现频率最高的那个分数。众数也属于整体度量,它的特点是用频数大小来呈现数据的集中趋势。因此,众数也是一个被用来反映考试总体状况的度量值。但是,众数的有效性会受限于样本数据的数量。例如,如果考生人数不多,就有可能会导致每个原始考分只出现一次,这样的话,就没有众数可寻了。当然,也存在着这样一种情况,如果考试成绩中有多个高频出现的分数,那么就会导致有多个众数出现。所以,众数只有在考试人数足够多,且考试成绩具有明显的集中趋势的情况下才显得有意义。
(4)利用平均分、中位数和众数对考试做趋势性分析
对考试原始分绘制频率分布曲线时,如果得到的是适度倾斜的单峰频率曲线,那么平均分、中位数和众数这三个集中量数之间,存在着如下关系:
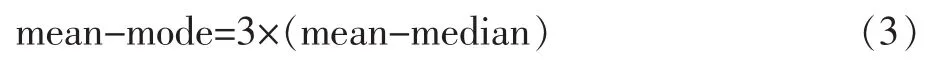
由此,我们可以发现对于能产生适度倾斜的原始分单峰频率曲线的考试来讲,就能通过该关系式推算出考试原始分数据集合中的众数。
对于呈正态分布的原始分单峰频率分布曲线(见图1)来讲,平均分、中位数和众数都是相同的中心值,这当然是一种理想化考试结果的呈现。它说明了就本次考试而言,考生群体学业水平能力以中等为主,有相对优秀和相对较差的学生存在,但不占主体。
对于呈正偏态分布的原始分单峰频率分布曲线(见图2)来讲,mode<median<mean;这表明考分高于平均分的考生低于50%。如果此时的平均分较低,则说明就本次考试而言,考生群体的学业水平能力较差(当然这种情况也有可能是因为试卷难度较高而造成的)。
对于呈负偏态分布的原始分单峰频率分布曲线(见图3)来讲,mode>median>mean,这表明考分高于平均分的考生超过了50%。如果此时的平均分较高,则说明就本次考试而言,考生群体的学业水平能力较高(当然这种情况也有可能是因为试卷难度较低而造成的)。
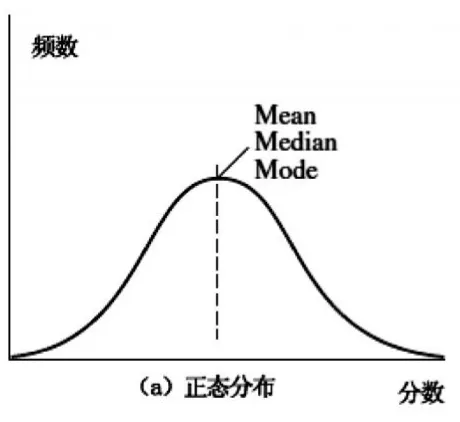
图1
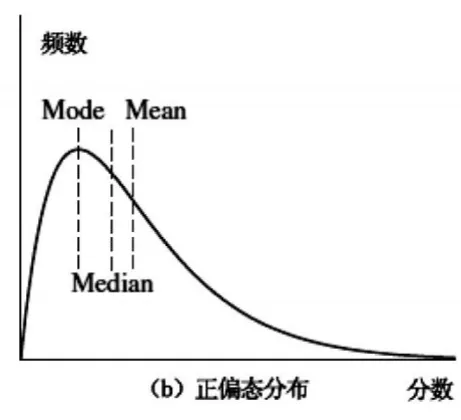
图2
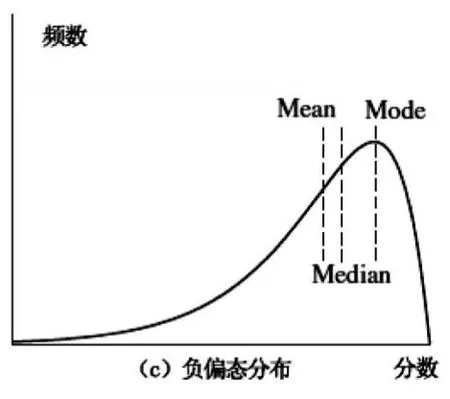
图3
2.度量考试分数的离散趋势特征
在分析数据集合的离散程度时最常用的度量有:极差(R)、标准差(σ)和中间四分位数极差(IQR),我们称之为差异量数。这三个差异量数可以用来描述一批分数的差异程度。如果说度量考试分数中心趋势特征的集中量数是一个中心点,它让所有分数围绕着它分布;那么用于度量考试分数离散趋势特征的差异量数,则是用于表示各分数与中心点之间的距离,它描述了分数与中心点之间存在的差异统计值。利用这三个差异量数对考试成绩进行数据离散趋势分析时,可以准确地了解参加考试的学生群体在学科学业水平上存在的差异状况。
(1)极差 (R)
极差(又称全距)是一组数据中的最大值与最小值之差。极差用R来表示:

在对考试成绩做统计分析时,极差就是一次考试中的最高分和最低分之差。极差在某种程度上反映了参与考试的学生群体,在学业水平上存在的最大差距。极差虽然计算简单、意义明确,但是它的大小完全由位于两个极端的分数来决定,它无法对位于两个极端分数之间的其他分数的差异性状况进行有效分析。因此,如果仅用极差来描述考试分数的整体离散趋势状况,效果肯定是很差的。就如同,如果一次考试的最高分是满分,而最低分是0分,那么就不存在极差的度量意义了。但是,我们还是可以利用极差粗略地了解关于某次考试学生成绩的最大差异。
(2)标准差(σ)
标准差是方差的平方根,又称为均方差,用σ来表示:

标准差是一个能够有效衡量、精确描述数据分散程度的差异量数。它能对一次考试分数,偏离平均分程度的大小给出明确的判断。如果标准差越小,考试分数就越向平均分集中,即分数的分布差异越小。反之,则说明考试分数离开平均分的程度增大,分数分布的差异也越大。一般情况下,如果考试分数的频率分布呈现正态分布,那么极差应该大致等于6个标准差(R≈6σ)。
组合使用极差和标准差这两个差异量数,可以准确有效地判断出数据集合的离散差异程度。特别是在教学质量分析中,极差和标准差的组合使用,可以准确有效地分析出考试分数的离散分布状况,并由此推断出参与考试的学生群体在学业水平上存在的差异和不同。当然,也可以依据这种分析对试卷的质量做出评判。例如,如果根据考试分数计算得到的极差和标准差均很小,则反映了考生的学业水平非常接近。但这种情况也很可能说明试卷的命题组卷出现了问题,导致无法拉开考生的成绩,进而也掩盖了考生实际学业水平的真实差距。反之,如果极差和标准差均很大,这就表明考生群体的学业水平整体差异性较大,高水平学生和低水平学生都很多。
(3)中间四分位数极差(IQR)
在按升序排列的数据集合中,第k个百分位数是指该数在数据集合中的定位,即,数据集合中有k%的数据小于或等于该数。据此定义,中位数就是第50个百分位数,第25个百分位数被称为第一四分位数(Q1),而第75个百分位数被称为第三四分位数(Q3)。而中间四分位数极差(IQR)就是指按升序排列的数据集合中,第三四分位数与第一四分位数的差值:

IQR值反映的是中间数值的分散程度,对于教学质量分析来讲,它描述的是原始考试分数集中分布的范围,反映了考生成绩的集中趋势状况。从使用经验上讲,一般一组数据中的可疑离群点(或称数据噪声),其位置基本位于高于第三个四分位或低于第一个四分位数的1.5 X IQR处。在教育质量分析中,利用这一方式可以有效地识别和剔除考分中的那些无意义的分数。例如,误将缺考学生的成绩(0分)纳入考分统计样本之中;由于特殊原因导致个别学生无法进行正常考试而产生不正常的低分;个别学生提前知道试卷答案得到了异乎寻常的高分。这些分数数值一般都有可能超过了四分位数极差值的1.5倍,这足以提醒分析人员倍加关注并确定是否要予以剔除,从而有效地减小其对考试评估分析的影响。
四、描述性数据汇总技术应用举例
在中小学基于考试成绩所做的教育质量分析中,我们可以利用中位数、两个四分位数(Q1、Q3)以及原始分的最小值和最大值这五个描述性数据度量值,总体概括出考生成绩的集中趋势和离散程度。在数据挖掘中,这种描述性数据汇总技术又被称之为五数概括(five-number summary),而利用盒状图又可以直观地呈现五数概括所要反映的数据特征。
图4给出的是一次区域性数学学科考试中,参加考试的每所学校的考试成绩的盒状图。盒子的上下两条底边,分别代表的是Q1和Q3两个四分位数,而盒子的高度就是中间四分位极差IQR。盒子中间的横线代表中位数。盒子上下两条线的末端,代表的是每所学校的最高考分和最低考分。由于在不出现极端考分数据值的情况下,在盒状图中使用平均分能更好反映各校考试成绩的总体趋势,因此此图中用平均分取代了中位数。另外,盒状图中两个四分位数(Q3、Q1)分别被调整为排名前25%学生和排名后25%学生的成绩平均分(分别被称为高分组平均分和低分组平均分),这也是为了更好的反映各校考生的考试成绩在上、下两端间的整体差距。
由图我们可以看到,利用平均分这个描述数据集中趋势的集中量数,很好地说明了各校学生成绩在区内的整体定位;而两个四分位数所形成的IQR这个用于描述数据离散趋势的差异量,也清晰地反映了各校学生学业水平的差异状况。
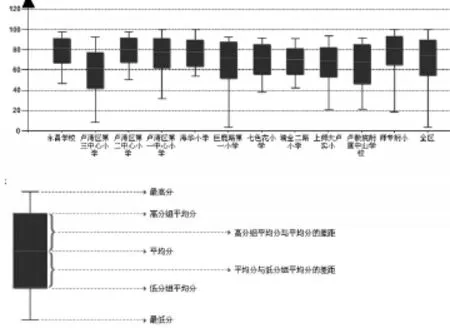
图4
五、结束语
用于度量考试分数中心趋势特征的平均分、众数和中位数,以及用于度量考试分数离散趋势特征的极差、标准差和中间四分位数极差,这些描述性统计量在中小学教学质量分析中的应用,可以帮助我们有效地理解原始考分数据的总体特征和分布情况。从数据挖掘的角度来看,我们应该充分理解这些描述性统计量的计算意义并合理地使用它们,形成科学准确的分析结果,挖掘出隐藏在考试成绩背后的知识信息。从而为教育管理部门监测区内学校教育质量、开展课程教学指导,提供有效的决策依据。
[1][加]Jiawei Han著;范明,孟小峰译.Micheline Kamber.Data Mining Concepts and Techniques,Second Edition[M].
[2]刘新平,刘存侠.教育统计与测评导论[M].北京:科学出版社,2003.
[3]雷新勇.考试数据的统计分析和解释[M].上海:华东师范大学,2007.
[4]杨思清.数据挖掘技术对提高教学质量的应用研究[J].黑龙江科技信息,2007(4).
[5]黄羿,马新强,武彤,唐作其,朱莹.基于数据仓库的学生成绩分析模型设计[J].信息技术,2007(2):18-23.
[6]李琳,徐雨明,孙士兵.数据挖掘在教学质量分析中的应用研究[J].衡阳师范学院学报,2009,30(3):86-88.
[7]郭晓利,郭平,冯力.基于数据挖掘技术的教学质量分析评价系统的实现[J].东北电力大学学报(社会科学版),2006,26(3):70-73.
(编辑:王晓明)
TP393
:A
:1673-8454(2017)07-0065-04
