基于无级变速器的混合动力汽车动态模式切换研究

王建德 周云山 阳辉勇 贾杰锋 李 泉

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

基于无级变速器的混合动力汽车动态模式切换研究

王建德 周云山 阳辉勇 贾杰锋 李 泉

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

对基于无级变速器的混合动力系统的结构及其工作模式进行分析，建立了动力学模型。针对伴随发动机启动的混合动力模式切换问题，提出了一种模糊推理与最优控制理论相接合的综合控制策略。首先基于驾驶意图采用模糊控制得到离合器接合时长，然后基于动力学模型采用动态规划得到离合器的最优传递转矩和发动机的最优目标转矩，再根据离合器最优传递转矩利用电机的快速响应性来实时调整电机输出转矩。通过试验对上述模式切换控制策略进行了验证。试验结果表明：该策略能够优化离合器滑摩时间，体现驾驶意图，实现模式切换的平顺性。

模式切换；驾驶意图；模糊控制；动态规划

0 引言

混合动力汽车具有多种工作模式，在模式切换过程中，由于各动力源的响应特性差异以及变速器、离合器的状态改变，可能造成发动机转矩或电机转矩突变，对车辆动力系统产生不可忽视的冲击。因此在模式切换时，需协调各动力源转矩的动态输出，实现动力传递的平顺性[1-3]。

国内外学者针对混合动力汽车模式切换进行了大量研究。童毅等[4]提出了发动机转矩开环+发动机动态转矩估计+电机转矩补偿的动态协调控制算法；闫晓磊等[5]采用了二次型最优控制算法；严运兵等[6]建立了转矩预分配+发动机调速+发动机动态转矩估计+电动机转矩补偿控制控制方法；叶明等[7]对机电式无级变速器(continuously variable transmission，CVT)提出了基于速比控制的模式切换策略；刘振军等[8]针对单电机CVT式混合动力汽车进行协调速比控制，制定转矩协调控制策略，采用电机补偿；尹安东等[9]采用了动态转矩协调控制策略；WU等[10]应用动态规划，提出最优控制方案；SIMITH等[11]采用一种简单鲁棒性好的控制算法，在模式切换过程能够减少离合器需求转矩与预估转矩的差值，更好地得到电机的补偿转矩。在诸多模式切换过程中，伴随发动机启动的模式切换，由于既有发动机的启动，又有离合器的控制，是混合动力汽车模式切换研究的难点[12]，因此本文重点研究纯电动模式到伴随发动机启动的驱动模式切换。

由于CVT速比在一定范围内连续可变，可最大程度地优化发动机和电机的工作区域，CVT已经在很多混合动力汽车上得到成功应用。本文以一种基于CVT的混合动力系统为研究对象，针对伴随发动机启动的模式切换过程，利用CVT速比连续变化的优势，采用了一种模糊推理与最优控制理论相接合的综合控制策略，实现了不同驾驶意图下的模式切换过程。

1 动力系统结构及工作模式

1.1 混合动力系统结构

图1所示为基于CVT的混合动力系统，主要由发动机、离合器、集成启动/发电一体化电机(integrated starter generator，ISG)、CVT及皮带传动启动/发电一体化电机(belt-driven starter generator，BSG)等部件组成。该系统取消了传统CVT中的液力变矩器，在液力变矩器原来的位置集成ISG和湿式离合器，离合器布置于ISG转子内部，离合器的控制集成到CVT中。ISG与CVT集成，并且省掉了CVT内部的前进/倒挡离合器，这样整个结构在轴向空间布置上具有明显的优势。该系统在发动机前端采用了BSG，取代了原有的发电机和启动电机，用于启动发动机和给蓄电池充电，同时可实现停车发电功能。

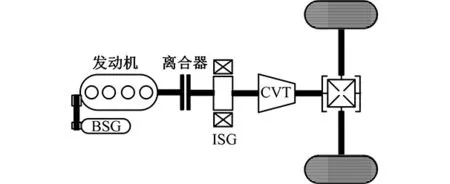
图1 混合动力系统结构Fig.1 The structure of hybrid electric system

1.2 系统工作模式

通过控制发动机、离合器、ISG和BSG的工作状态，该混合动力系统可以实现纯电动、发动机驱动、并联混合驱动、发动机主动充电、能量回收、停车发电、串联混合驱动等多种工作模式，如表1所示。

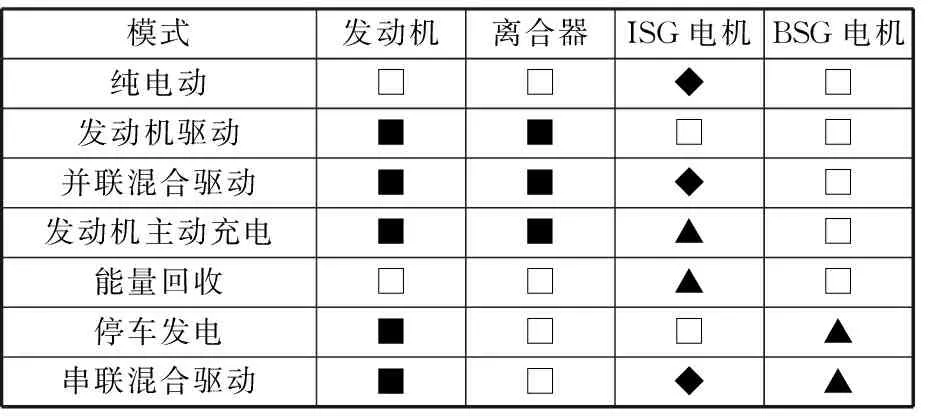
表1 混合动力系统工作模式

□:不工作/分离；■：工作/接合；◆：驱动；▲：发电

2 模式切换过程动力学模型

在建立车辆动力系统模式切换过程模型时，忽略传动部件之间的传动效率，并将系统各部件视为刚体，将离合器两侧的所有质量等效到离合器，建立图2所示的动力学模型。

图2 动力系统模式切换过程等效简化模型Fig.2 Simplified model of hybrid electric system mode transition

图2中，JICE、Jout分别为发动机侧和电机侧等效转动惯量，kg·m2；ωp、ωs为离合器主从动侧转速，r/min；TICE、Tf、Tc、Tem、Tload分别为发动机输出转矩、发动机阻力矩、离合器传递转矩、电机转矩和变速器输入端等效阻力矩，N·m。

车辆行驶阻力Fr由空气阻力、坡道阻力和滚动阻力组成，即

(1)

式中，m为整备质量，kg；A为迎风面积，m2；Cd为风阻系数；f为滚阻系数；α为坡度，rad；v为车速，km/h;g为重力加速度。

变速器输入端的等效阻力矩为

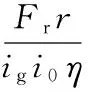
(2)

式中，η为传动系统的效率；r为轮胎半径，m；ig为CVT速比；i0为主减速比。

离合器从动侧转速ωs和电机侧等效转动惯量Jout分别为

(3)

(4)

式中，Jw、Jg、Jem、Jc分别为车轮、CVT、电机和离合器从动部分的转动惯量，kg·m2。

离合器滑摩过程中的动力学方程为

(5)

(6)

离合器锁止后，由于ωp=ωs，此时动力学方程为

(7)

3 模式切换控制策略

研究表明，加速踏板开度和加速踏板开度变化率可反映驾驶意图，当加速踏板开度大且变化率大时，表明驾驶员希望车辆快速进入动力更强的工作模式，应优先考虑动力性；反之，优先考虑平顺性与舒适性，因此在模式切换控制策略制定时需要考虑驾驶意图。

在伴随发动机启动的模式切换中，既有纯电动模式到发动机驱动模式，也有纯电动模式到混合驱动模式，取决于驾驶员意图，在此以纯电动模式切换到发动机驱动模式为例，分析其模式切换过程，如图3所示。首先通过BSG快速启动发动机，neo为判断发动机启动完成的最低转速，然后控制发动机转速ne同步电机转速nm，待转速差小于阈值Δnh后，进行离合器滑摩控制。当转速差小于阈值Δnl后，离合器完全接合。在整个过程中通过电机转矩补偿和CVT速比控制，实现模式切换过程中的动态协调控制，直到发动机协调输出转矩Tcoo与驾驶员需求转矩Treq之差的绝对值小于阈值ΔT。电机空转，从而完成从纯电动到发动机驱动的模式切换。

图3 纯电动切换到发动机驱动模式流程图Fig.3 Flow chart of mode transition from electric driven to engine driven

表2给出了Δnh模糊控制规则，模糊集合均为{S，MS，M，MB，B}，此处，S、MS、M、MB、B分别表示参数取值小、中小、中、中大、大。该表的制定源于专家系统经验，一般而言在较小的加速踏板开度和加速踏板变化率条件下，取较小的转速偏差，这是因为基于驾驶意图，此时驾驶员对扭矩响应意愿不强，可以进行发动机和电机转速较为精确的调节。而较大的加速踏板开度和加速踏板变化率条件下，允许较大转速差，以快速响应驾驶扭矩需求。

表2 发动机转速同步转速差阈值Δnh的模糊控制规则

图4为模式切换的控制原理图，将模式切换过程分为三个阶段分别进行控制。

图4 模式切换控制原理图Fig.4 Control principle scheme of mode transition

(1)发动机启动阶段。首先控制BSG快速启动发动机，BSG以最大转矩将发动机加速至怠速附近。由于此时离合器完全分离，发动机的动力没有传递到车轮，所以发动机的启动不会影响车辆行驶的平顺性，这是采用BSG启动发动机的优势。

(2)发动机转速同步阶段。当发动机启动后，处于空载，无扭矩输出，驾驶员的加速踏板并不直接输入给发动机管理系统，而是通过整车控制器(hybrid control unit，HCU)根据分配的发动机转矩来输出伪加速踏板开度αp给发动机管理系统。一方面HCU采用PID闭环调节节气门开度控制发动机转速跟随电机转速，另一方面通过CVT的速比调节保持电机转速在一定范围内，从而实现发动机与电机之间的转速快速同步，以减少二者之间的偏差。

发动机的节气门开度为

(8)

式中，e(t)为目标转速与实际转速之差；KP、KI、KD分别为比例、积分、微分系数。

电机的目标转矩为

Temcmd=min(Tload,Temmax(ωs))

(9)

式中，Temmax(ωs)为电机在ωs转速下的最大输出转矩。

(3)离合器接合阶段。当离合器主从动盘转速差|ne-nm|<Δnh时，离合器滑摩接合，此时需要根据离合器的转矩调整电机的输出转矩进行转矩补偿，同时需要基于驾驶意图，控制离合器接合时长。离合器接合太快会导致其传递的转矩发生突变，从而超过了电机进行转矩补偿的速度和精度；离合器接合太慢会增加离合器片的磨损。合理控制离合器的接合速度(油压变化或转矩变化)是该阶段控制策略的关键[13]。

本文通过电机转矩补偿+CVT速比控制，使离合器在接合时从动端的转速基本保持不变，以减小离合器的接合过程对车辆冲击度产生的影响，保证切换过程中的平顺性。该阶段离合器的控制主要是使接合过程中滑摩功最小。

离合器传递的转矩与油缸的压力之间存在线性关系：

(10)

式中，sign(·)为符号函数；Δω为离合器主从动盘转速差；μd为摩擦副的动态摩擦因数；Z为离合器的摩擦副个数；Ap为活塞作用面积；Pn为油缸的压力；Ri、Ro分别为摩擦片内外半径。

因此，离合器的转矩控制与油压控制可视为同一个问题。

本文在离合器接合阶段控制策略的基本思路是，首先根据驾驶意图(离合器开始接合时刻的加速踏板开度α及加速踏板开度变化率Δα)，通过模糊推理得到离合器接合的时长，然后利用动态规划在该时长内对离合器转矩进行最优控制，最后利用电机的快速响应性和转矩精确控制根据驾驶员需求转矩和离合器所传递的转矩来调整电机的输出转矩。

在计算离合器接合时长tf时，将离合器开始接合时刻的α、Δα和tf使用三角形函数进行模糊化，模糊集合均为{S，MS，M，MB，B}，模糊控制规则如表3所示[14]。模糊推理后经过反模糊化可得到离合器接合时长tf。

表3 离合器接合时间tf的模糊控制规则

确定离合器接合时长后，需在确定时间段内控制发动机转矩和离合器转矩使该时间段内离合器的总滑摩功最小。由于发动机动态特性的滞后性，发动机目标转矩为

(11)

式中，TICEcmd为发动机目标转矩；τe为滞后时间。

由式(5)和式(11)联立，选取状态变量为x1=ωp、x2=TICE，控制变量为u1=TC、u2=TICEcmd，可得如下状态方程：

(12)

其中，由于经转速同步后的发动机转速变化范围不大，发动机阻力矩Tf可视为定值。

将上述状态方程按时间步长Δt离散化后可得到系统的状态转移方程：

(13)

(14)

系统的性能指标，即总滑摩功为

(15)其中，ωs为定值，其值由模式切换开始时的电机转速所决定。L(x(k),x(k+1))表示从第k阶段到第k+1阶段的滑摩功。将式(14)代入式(15)，可以根据每个阶段的始末状态直接计算滑摩功。

为简化问题求解，将状态变量的取值进行网格化。在离合器接合过程中，发动机的转速和转矩在每个阶段内不应该出现减小的情况。故状态变量和控制变量的约束条件为

(16)

针对上述离散型最优控制问题，采用动态规划的方法进行求解，具体过程如图5所示。该方法通过直接遍历每个阶段始末状态的可达状态集X(k)和X(k+1)来计算滑摩功，最后由最优状态序列X*根据式(14)计算出最优控制的决策序列U*。图中，阶段总数N由离合器接合时长tf与步长Δt(取0.1 s)的比值取整得到；初始状态X(1)为离合器开始接合时发动机的转速和转矩；末端状态X(N+1)为电机转速ωs和模式切换结束时所要求的发动机转矩；X(i,k)为可达状态集X(k)中的第i个元素，J*(X(i,k))为从状态X(i,k)到达终点状态X(N+1)的最小滑摩功。

图5 动态规划法的求解流程Fig.5 Solving process of dynamic programming

根据动态规划算法可以同时求解出离合器最优传递转矩和发动机最优目标转矩。发动机管理系统可根据发动机最优目标转矩进行转矩控制。在离合器接合的过程中，电机的目标转矩为

(17)

本文采用离线计算、在线查表的方法将动态规划应用于实时控制，即通过N、ωp(1)、ωp(N+1)、TICE(1)和TICE(N+1)查表可得到离合器转矩和发动机命令转矩最优控制轨迹。由于离合器接合时间较短，该过程的最优控制采用开环控制。

4 结果与分析

模式切换试验在转鼓试验台上进行，如图6所示。分别在平缓加速、中等加速和紧急加速下进行试验，车辆从静止状态纯电动起步，根据能量管理策略进行模式切换。基于加速踏板开度及其变化率和车速计算驾驶员需求转矩，根据所需转矩进行工作模式的切换，如在平缓加速和中等加速时进入发动机驱动模式，而在紧急加速时进入混合驱动模式。在此不做能量管理策略的研究，只进行伴随发动机启动的模式切换平顺性的研究。

图6 转鼓试验台上进行模式切换试验Fig.6 Mode transition test on chassis dynamo-meter

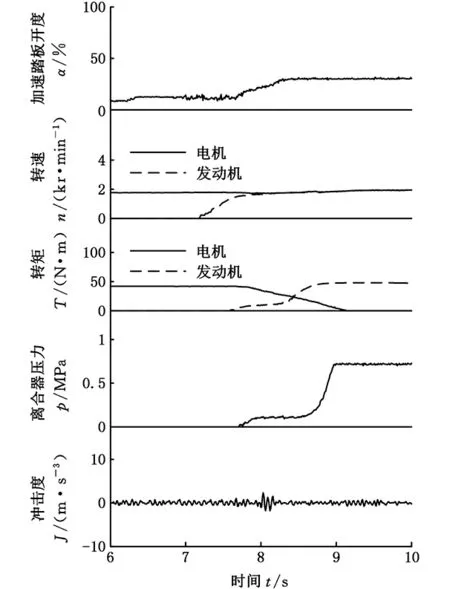
图7 平缓加速时模式切换过程Fig.7 Mode transition under gentle acceleration

图7所示为平缓加速时的模式切换过程，从6.9s开始进入模式切换，首先启动发动机，7.1s时发动机转速开始同步电机转速。7.7s时开始离合器接合，此时加速踏板开度为30.28%，加速踏板开度变化率为54%s-1。离合器接合过程中，随着发动机动力的介入，电机逐渐退出工作。模式切换过程中各参数的变化，如图7所示。

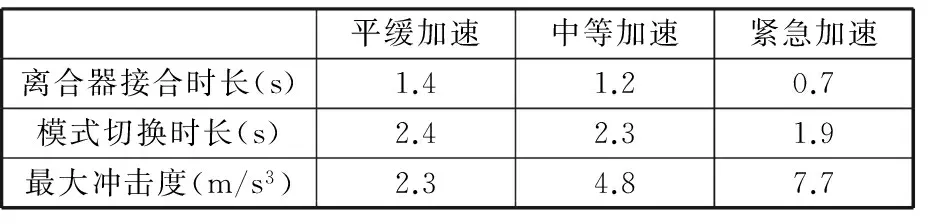
图8和图9所示分别为中等、紧急加速时的模式切换过程，不同驾驶意图下的模式切换时间和冲击度大小如表4所示。从表中数据看出，在不同的驾驶意图下，所体现出的模式切换时间和冲击度大小是不一的，这是由于所采用的控制策略，在非紧急驾驶意图下，优先考虑整车平顺性，采用较长的离合器接合时间；在紧急驾驶意图下和保证整车平顺性的前提下，优先满足整车动力性，缩短离合器滑摩时间。

图8 中等加速时模式切换过程Fig.8 Mode transition under moderate acceleration

图9 紧急加速时模式切换过程Fig.9 Mode transition under urgent acceleration

平缓加速中等加速紧急加速离合器接合时长(s)1.41.20.7模式切换时长(s)2.42.31.9最大冲击度(m/s3)2.34.87.7

由表4可以看出，该策略的模式切换时间最长为2.4 s，最大冲击度也仅为7.7 m/s3，体现出了良好的模式切换效果。这是因为该控制策略是通过BSG快速启动发动机，待发动机转速同步后进行离合器控制的。一方面，发动机的启动不影响模式切换平顺性，减少了模式切换过程的冲击因素；另一方面，离合器在主从动侧转速差较小的时候接合，缩短了离合器接合时间同时降低了接合冲击强度。

5 结论

(1)对一款BSG联合ISG的CVT型并联混合动力系统的结构和工作模式进行分析，建立了动力学模型，为控制策略提供了理论依据。

(2)提出了发动机启动、发动机转速同步和离合器接合的三阶段模式切换方法，提高了模式切换的平顺性且延长了离合器的使用寿命。

(3)提出了模糊推理与最优控制理论相接合的综合控制策略，基于驾驶意图采用模糊控制方法控制离合器接合时长，利用动态规划在该时长内对离合器转矩进行最优控制，协调模式切换过程中的转矩变化，为试验研究提供了基础。

(4)试验结果表明，该策略能够优化离合器滑摩时间，体现驾驶意图，并且能够有效减小发动机启动模式切换过程中的转矩波动和整车的冲击度，提高车辆的行驶平顺性。模式切换过程需要发动机、电机、CVT和离合器共同作用，本文对离合器控制方法没有考虑温度和磨损程度对其特性的影响，后续将考虑对这些因素作修正。

[1] HU X, MARTINEZ C M, EGARDT B, et al. Multi-objective Optimal Sizing and Control of Fuel Cell Systems for Hybrid Vehicle Applications[C]//Europena Control Conference. Linz, 2015:2559-2564.

[2] KUM D. Control of Engine-starts for Optimal Drivability of Parallel Hybrid Electric Vehicles[J]. Journal of Dynamic Systems Measurement & Control, 2013, 135(2):450-472.

[3] 刘翠, 初亮, 郭建华, 等. 并联混合动力汽车驱动模式切换扭矩协调控制[J]. 华中科技大学学报(自然科学版), 2013, 41(12):85-89. LIU Cui,CHU Liang, GUO Jianhua, et al. Torque Coordination Algorithm for Driving Mode-transition of PHEV[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2013,41(12):85-89.

[4] 童毅, 欧阳明高, 张俊智. 并联式混合动力汽车控制算法的实时仿真研究[J]. 机械工程学报, 2003, 39(10):156-161. TONG Yi, OUYANG Minggao, ZHANG Junzhi. Real-time Simulation and Research on Control Algorithm of Parallel Hybrid Electric Vehicle [J]. Chinese Journal of Mechanical Engineering, 2003, 39(10):156-161.

[5] 闫晓磊, 钟勇, 钟志华. HEV传动系统动力平顺切换最优控制的研究[J]. 汽车工程, 2008, 30(4):309-329. YAN Xiaolei, ZHONG Yong, ZHONG Zhihua. A Research on Optimal Control for Power Smooth Shifting in HEV [J]. Automotive Engineering, 2008, 30(4):309-329.

[6] 严运兵, 颜伏伍, 杜常清. 并联混合动力电动汽车动态协调控制策略及仿真研究[J]. 中国机械工程, 2010, 21(2):234-239. YAN Yunbing, YAN Fuwu, DU Changqing. Research on Strategy and Simulation for Dynamic Coordinated Control of PHEV[J]. China Mechanical Engineering, 2010, 21(2):234-239.

[7] 叶明, 程越, 舒红. 机电式CVT插电式混合动力系统模式切换控制[J]. 中国机械工程, 2012, 23(5):585-589. YE Ming, CHENG Yue, SHU Hong. Mode Shifting Control of Plug-in Hybrid Electric System Equipped with Mechanic-Electric CVT [J]. China Mechanical Engineering, 2012, 23(5):585-589.

[8] 刘振军, 赵江灵, 秦大同, 等. 混合动力汽车由纯电动工况起动发动机特性研究[J]. 机械设计与制造, 2013(12):101-104. LIU Zhenjun, ZHAO Jiangling, QIN Datong, et al. Pure Electric Mode Starting Engine Performance Research of HEV[J]. Machinery Design & Manufacture, 2013(12):101-104.

[9] 尹安东, 宫闪闪, 江昊, 等. 动态转矩协调的ISG混合动力系统控制策略[J]. 电子测量与仪器学报, 2013, 27(2):145-150. YIN Andong, GONG Shanshan, JIANG Hao, et al. Control Strategy of ISG Hybrid System Based on Dynamic Torque Coordination [J]. Journal of Electronic Measurement and Instrument, 2013,27(2):145-150.

[10] WU Guang, ZHANG Xing, and DONG Zuomin. Optimal Control for Ensured Drivability of Parallel HEVs/PHEVs during Mode Transition[J]. SAE Technical Papers， 2014-01-1895.

[11] SMITH A, BUCKNOR N, YANG Hong, et al. Controls Development for Clutch-assisted Engine Starts in a Parallel Hybrid Electric Vehicle[C]// SAE 2011 World Congress & Exhibition. Detroit, 2011-01-0870.

[12] 秦大同, 尚阳, 杨官龙. 插电式混合动力汽车纯电动行进间启动发动机的平顺性控制[J]. 重庆大学学报, 2015, 38(4):1-9. QIN Datong, SHANG Yang, YANG Guanlong. The Ride Comfort Control of PHEV during Engine Starting In-motion Process[J]. Journal of Chongqing University, 2015, 38(4):1-9.

[13] 杜波, 秦大同, 段志辉, 等. 新型并联式混合动力汽车模式切换协调控制[J]. 中国机械工程, 2012, 23(6):739-744. DU Bo, QIN Datong, DUAN Zhihui, et al. Coordinated Control for Mode-switch of a New Parallel HEV[J].China Mechanical Engineering, 2012, 23(6):739-744.

[14] 张飞铁, 周云山, 薛殿伦. CVT起步离合器模糊控制算法研究[J]. 湖南大学学报(自然科学版), 2006, 33(5):57-60. ZHANG Feitie, ZHOU Yunshan, XUE Dianlun. Research on Fuzzy Control Algorithm of CVT Starting Clutch [J]. Journal of Hunan University (Natural Sciences), 2006, 33(5):57-60.

(编辑 王旻玥)

Research on Dynamic Mode Transition of Hybrid Electric Vehicle Based on Continuously Variable Transmission(CVT)

WANG Jiande ZHOU Yunshan YANG Huiyong JIA Jiefeng LI Quan

State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082

For a hybrid electric system based on continuously variable transmission(CVT), its structures and working modes were analyzed, and a kinetics model was established. A comprehensive control strategy combining fuzzy reasoning and optimal control theory was proposed for mode transition with engine starting. In the strategy, a clutch combination time was firstly obtained by fuzzy control based on driving intention. Then, an optimal clutch transmission torque and an optimal engine target torque were determined through the kinetics model with dynamic programming. Finally, the output torque of the motor was adjusted in real time according to the optimal clutch transmission torques by making use of the quick responsiveness of motor. Experiments were performed to verify the proposed control strategy. The experimental results show that the control strategy may optimize the clutch slip time based on driving intention, and achieve the smoothness of mode transition.

mode transition; driving intention; fuzzy control; dynamic programming

2016-07-04

国家国际科技合作专项(2014DFA70170)

U469.72

10.3969/j.issn.1004-132X.2017.10.019

王建德，男，1983年生。湖南大学机械与运载工程学院博士研究生。主要研究方向为新能源汽车、车辆动力传动与控制。E-mail：wjdcvt@163.com。周云山，男，1957年生。湖南大学机械与运载工程学院教授、博士研究生导师。阳辉勇，男，1986年生。湖南大学机械与运载工程学院博士研究生。贾杰锋，男，1990年生。湖南大学机械与运载工程学院硕士研究生。李 泉，男，1976年生。湖南大学机械与运载工程学院博士研究生。