利率挂钩产品定价研究*
——以区间累积型产品为例
2017-06-05哈尔滨工程大学经济管理学院吕彦昭伍晓静原艺
哈尔滨工程大学经济管理学院 吕彦昭 伍晓静 原艺
利率挂钩产品定价研究*
——以区间累积型产品为例
哈尔滨工程大学经济管理学院 吕彦昭 伍晓静 原艺
利率挂钩产品是市场上重要的结构性金融产品,其公平定价是买卖双方关注的重点。本文通过构建利率挂钩产品定价的一般模式,从而为此类产品进行公平定价。该产品定价的一般模式包括利率期限结构的确定、产品现金流的分解与确定、产品的定价、产品价格的敏感性分析等,使用LMM市场利率模型和蒙特卡罗模拟估计贴现率和挂钩利率的期限结构,从而确定产品未来现金流,将产品现金流贴现就得出产品的理论价格。选取区间累积型利率挂钩产品作为样本进行定价。结果显示:该产品为折价发行,值得投资者投资;敏感性分析结果显示,价格与产品期限的变动正相关,价格与贴现率及其波动率的变动负相关。
利率挂钩产品 公平定价 LMM模型 敏感性分析
一、引言
国内金融产品市场日益活跃,结构性金融产品蓬勃发展。截至2014年8月底,全国商业银行结构性产品发行量已达1758个。2015年,银率网统计的32家商业银行发行的结构性理财产品总量为3754个,利率挂钩型产品为发行量最大的结构性产品之一。因此,对该类产品进行定价研究,在投资决策、金融产品研发等方面具有重要意义。
二、文献综述
国内外学者在利率挂钩型产品的实证研究方面有较多的成果。在国外,Chen、Taylor和Wu(2001)研究市场指数联动债券的定价,并将MITTS视为零息债券与欧式买权的组合。Sascha、Carsten和Klaus(2003)使用欧洲期货交易所的看涨期权,运用复制技术比较结构性产品的价格,并分别从产品类型、基础产品、发行者方向研究这些结构性产品的价格差异。Szymanowska、Horst和Veld(2007)发现阿姆斯特丹证券交易所的反向可转换债券有5%水平的溢价率,而反向障碍可转换债券却是折价发行的。Wallmeier和Diethelm (2009)运用Chen、Chung和Yang(2002)提出的多叉树模型研究瑞士市场上嵌入障碍期权的多资产可转换债券定价,认为产品的定价与债券类型相关,投资者容易低估衍生部分价值而高估固定收益部分价值。在国内,成黎明(2009)分别用HW模型、BDT模型和BK模型对我国市场上的含权债券进行了定价。刘昭文(2010)用修正的Heston模型、马尔科夫链的蒙特卡罗模拟方法对触发式利率挂钩产品进行定价。李勇飞、侯志强(2013)运用最小二乘蒙特卡罗和Libor Market Model(LMM市场利率模型)对美式可赎回债券定价。孙学彬和潘永泉(2014)基于未校准的LMM市场利率模型对一款区间累积利率挂钩产品进行了定价。
大多数研究将利率挂钩产品拆解成“固定收益部分+期权部分”的形式,并分别进行定价,其中的期权定价和利率期限结构估计为研究的重点内容。在期权的定价方面,经典的B-S期权定价模型并不一定能准确地描述各类标的资产价格的变化过程,在实证研究中广泛使用的是数值分析方法,包括树图方法、蒙特卡罗模拟和有限差分等。对于贴现率及挂钩利率的估计,若想要模拟未来的利率变动过程来得到未来利率的估计,动态模型比静态模型更好,其利率期限结构会与市场真实情况更相近。对于需要估计远期利率的问题来说,以基于刻画远期利率变动的HJM模型和LMM模型为佳,且LMM市场利率模型计算的利率更加贴近实际情况(LMM有两个优点:一是LMM模型上的校准比较容易;二是LMM模型是建立在市场上可以观察到的利率的基础上)。对于结构性产品风险的研究,学者普遍从敏感性分析和避险参数分析两方面着手,但专门对利率挂钩产品风险的研究较少。本文尝试构建利率挂钩产品定价的一般模式,使用LMM市场利率模型和蒙特卡罗模拟,选取区间累积型利率挂钩产品进行定价,并运用敏感性分析方法来分析利率挂钩产品定价的影响因素。
三、利率挂钩产品定价的一般模式
一般情况下,结构性产品定价模式主要由现金流的分解与确定、贴现率的确定、产品定价三部分组成。而利率挂钩产品需要估计收益率的挂钩利率,这是利率挂钩产品定价区别于其他类型产品定价之处,对挂钩利率的估计与对贴现率的估计方法相同,可以把二者计算步骤合并。另外为探究各变量对定价的影响,应增加敏感性分析部分。因此,本文构建了利率挂钩产品定价的一般模式,其具体步骤包括:第一步,利率期限结构的确定:选择LIBOR市场利率模型估计出所需的挂钩利率和贴现率;第二步,产品现金流的分解与确定:将产品未来现金流拆分为“固定收益证券+利率期权”的形式,分别确定两部分的现金流或收益率、现金流发生的时间;第三步,产品的定价:用估计出的贴现率将固定收益部分和期权部分的现金流贴现,加总即得到产品的理论价格;第四步,敏感性分析:改变定价中各输入变量数据,分析它们的变化对价格的影响情况。
(一)利率期限结构的确定
(1)利率模型的选择。利率模型选择的标准主要是计算结果尽量与市场利率的期限结构相符,并且模型尽量简单且有效。本文选用动态利率模型,考虑利率的均值回复特性,增加了对利率动态变化的刻画。本文选择Brace、Gatarek和Musiela(1997)等提出的LIBOR市场利率模型(简称LMM模型或BGM模型)。其优点在于:它用金融市场上可以直接观测到的利率和市场隐含波动率作为输入参数进行计算,计算结果与市场实际情况更加吻合;模型考虑利率的均值回复性,波动率模型可以单独设置;模型适用于描述远期利率的动态变化,比同样刻画远期利率动态过程的HJM(1992)模型简单实用。
(2)利率期限结构的计算。利率期限结构的计算相对复杂。首先,要确定模型所需的期初远期利率,可以用市场上的利率报价作为即期利率计算远期利率,也可以用国债报价计算出的国债收益率曲线作为即期利率。其次,波动率的期初数据可通过计算历史波动率或隐含波动率获得,而由于市场上远期利率波动率是时变的,需选取适当的波动率模型描述未来波动率的形式以代入利率模型。最后,由于较复杂的利率模型的方程没有显示解,需选用数值方法来计算,本文选择蒙特卡罗模拟法进行计算,该方法计算相对简便、适合路径依赖型期权定价。图1描述了利率期限结构的计算过程,其中虚线表示该过程的样本选取与计算方法并不唯一。

图1 利率模型的一般计算过程
一是期初利率期限结构的确定。对于LMM模型,其期初的输入数据是0时观察的瞬时远期利率,若要求得瞬时远期利率,则需先得出期初的即期利率曲线。
期初即期利率曲线的计算,即期利率曲线的估计主要运用静态利率模型。当能够从市场上获取离散的即期利率时,可直接采用曲线拟合的方法求出即期利率曲线。由于挂钩利率有每日市场报价,因而选取这种方法估计挂钩利率的即期利率曲线。当市场上不能获取即期利率报价时,就需运用息票剥离法计算国债市场的即期利率,而后运用曲线拟合方法求出即期利率曲线,这里运用三次样条函数描述国债即期利率曲线。贴现率的即期利率用此方法计算。
期初远期利率的计算。得到期初即期利率曲线之后,就可求出相应的期初远期利率期限结构。在连续计息假设下,由即期利率计算远期利率的公式为:

其中,r1是[0,t1]期间的即期利率,r2是[0,t2]期间的即期利率,f1,2是[t1,t2]期间的远期利率。这里的利率都为连续复利计息的利率。
二是波动率的确定。标的资产的波动率是结构性产品定价的一个重要输入变量。本文中挂钩的远期利率波动率选择隐含波动率,贴现率波动率则选择国债市场历史波动率。
利用利率上限期权报价(Cap)求隐含波动率。当市场上存在相关利率期权报价时,可通过它们求得隐含波动率。由于利率上限期权(Cap)存在市场报价,用其价格可求出隐含波动率。利率上限期权(Cap)是由一系列不同时间段、相同执行价的利率上限子期权(Caplet)组成的利率衍生产品,它在利率上升时会锁定最高利率来保护浮动利率债务。利率上限子期权则是基于短期利率(浮动利率)的看涨期权。一般,Cap的市场报价是波动率的报价,此时一般用BS模型计算出Cap的期权价格。由于Cap由一系列Caplet组成,所以Cap的价格是一系列Caplet价格之和。Caplet是一种欧式期权,它的价格可以由BS模型计算,0时观察的[Ti-1,Ti]Caplet价格公式为

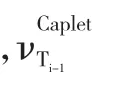

其中,j表示Caplet的总期数。另外,可以由Cap的报价波动率计算它的实际市场价格,公式为

其中为[Ti-1,Ti]期间Cap的报价波动率。在无套利条件下,Cap的理论价格与实际价格相等,就可由Cap报价计算隐含波动率νi。
远期波动率形式。为应用LMM模型,需确定波动率在远期的变化形式。为简化模型的参数估计,通常假设远期波动率为分段常数形式,波动率与其所在的时间有关。Brigo和Mercurio(2001)将分段常数形式的波动率归纳为五种不同的形式,本文选择常用的只与剩余期限有关的远期波动率模型,该模型参数估计较少,计算方便。
假设远期利率距离到期日的时长是影响波动率的唯一因素,且分段常数形式的远期波动率在每个期间(Tm-2,Tm-1]内为常数,Tm-2 该模型的波动率中所需要估计的变量只有M个,为η1,η2,...,ηm。波动率数据来源于市场上的利率上限期权报价Cap的隐含波动率。 三是利率模型的计算。利率模型的计算主要有偏微分方程法、树图法、有限差分法以及蒙特卡罗模拟。实证分析中选取一款区间累积型利率挂钩产品,该产品的收益率取决于挂钩利率处于设定区间内的天数,因而收益的计算具有路径依赖的特点,由此选择蒙特卡罗模拟方法来估计未来利率走势。该方法的基本思想是:对所求的问题建立随机概率模型,使它的某些变量是问题的解,由于随机概率模型可由各种概率分布构成,通过产生已知随机概率的随机数计算变量的统计特征,得出求解变量的近似值。在估计利率走势中,蒙特卡罗方法首先通过生成随机数模拟利率变化的多个路径,从而计算出利率走势的期望及产品现金流入的期望值,即得到利率期权的价格。 (二)产品现金流的分解与确定产品现金流的分解分为以下几步: (1)将产品的现金流分解为固定收益证券和利率期权两部分,这里的固定收益部分多为零息债券和附息债券的形式,而利率期权则有很多种,如看涨/看跌欧式期权,障碍期权、亚式期权等。 (2)根据产品收益的特点确定固定收益部分现金流发生的时间以及相应的现金流大小,现金流大小可根据息票率求得,息票率一般是利率挂钩产品的最低收益率; (3)剔除固定收益部分未来现金流,剩余部分为期权未来现金流。现金流发生的时间及计算方式可根据具体产品直接获得,而现金流的数额则取决于挂钩利率。 (三)产品的定价理论上,任何一种金融产品的价值等于该产品给投资者带来的未来现金流的现值。对产品固定收益部分和利率期权部分的定价也应用这种思想,用估计出来的贴现率将估计的全部现金流进行贴现,所得现值之和即为利率挂钩产品的理论价格。 (四)产品价格的敏感性分析由于在产品定价过程中,主要的输入变量是挂钩利率及其波动率、贴现率及其波动率的期初数据。为进一步分析价格的影响因素,对产品定价进行敏感性分析,以考察输入变量的改变对产品价格的影响情况。 (1)挂钩利率的变化会直接影响产品现金流,最终改变产品价格。但由于不同利率挂钩产品的收益计算方式不同,最终价格的变化情况也不尽相同。例如,对于看涨类型的产品,挂钩利率越高,收益就会越高,而对于看跌类型的产品则恰恰相反。 (2)挂钩利率的波动率也会对产品的价格产生影响,但它的变动对不同类型产品的价格影响方式不同。例如对于区间累积型产品,若波动率很大,则挂钩利率超过预设利率范围的机会大大增加,投资的收益就可能会因此减少。但对于一般看涨产品,波动率只影响挂钩利率的波动程度,却不能影响它的波动方向,对产品价格的影响方向则不甚明确。 (3)贴现率对产品价格的影响源于贴现过程。当期初利率期限结构曲线向下平移时,意味着贴现率会降低,产品的价值则会随之增加;当曲线向上平移时,贴现率会升高,产品价值则随之减少。 (4)与挂钩利率波动率相似,贴现率波动率的变化也会影响产品的定价,但其只影响贴现率的波动幅度而不能影响方向,因此无法从理论分析获得它对产品价格的作用情况,有待进一步考察。 在国内市场中,区间累积型利率挂钩产品是常见的产品类型。本文以平安银行2014年发行的挂钩LIBOR的区间累积型产品为例,应用前文所构建的定价模式对该产品进行定价。样本产品是平安银行“私人银行专享”结构类(挂钩利率)2014年34期人民币理财产品,存续期为185天,销售期从2014年5月26日到2014年5月29日,产品投资期从2014年5 月30日(包括该日)到2014年12月1日(不包括该日)。产品的收益与国际市场美元3个月LIBOR挂钩。另外,产品100%本金安全保障,衍生品部分投资于利率衍生产品市场。该产品的收益计算方法为: 投资者获得的收益率=潜在年化收益率×(实际投资天/365)×(处于累积区间内的日数/日历数) 其中,累积区间为[0.00%-5.00%](包括边界),潜在年化收益率为4.80%。 (一)利率期限结构的计算 (1)期初挂钩利率的估计。在LMM模型计算中,首先计算期初即期利率。挂钩利率LIBOR有每日市场报价,因报价利率是简单年利率,所以首先将其转化为连续复利的利率。转化后期初2014年5月26日的市场LIBOR数据见表1: 表1 LIBOR数据 由于需要得到期初即期利率曲线,基于三次样条插值方法对离散的即期利率进行插值,得出期初即期利率曲线。由于需要以3个月远期利率作为LIBOR市场模型的输入数据,因此根据公式(1)计算获得产品发行当日的3个月LIBOR远期利率曲线如图2。 图2 期初3个月期LIBOR远期利率曲线 (2)期初贴现率的估计。对于贴现率的估计,由于样本产品在国内发行,本文选取国债市场的即期利率数据作为计算贴现率的基础数据。首先,选取20个市场上交易的期限不同的国债,利用息票剥离方法计算出国债市场的即期利率。应用三次样条插值法,得到国债市场期初即期利率曲线。最终需估计出的贴现率是期末观察的185天的远期利率f(188,188,373),因而仍用公式(1)计算期初6个月期的远期利率曲线如图3。 图3 国债市场期初6个月远期利率曲线 (3)挂钩利率波动率的估计。本文使用分段常数形式的波动率来描述远期LIBOR利率的瞬时波动率。利用市场上提供的Cap报价和利率触发线计算出隐含波动率作为模型中的远期利率瞬间波动率。先要从市场上取得Cap波动率报价(见表2)。 表2 Cap波动率报价 Cap报价是Cap所在区间内的平均波动率。利用市场上各年期Cap报价反推出各个不同区间的Caplet波动率,也就是模型中所涉及的3个月远期利率波动率。假设Cap所包含的每个Caplet(3个月期)的波动率是相等的,以3个月为时间间隔,根据公式(2)、(3)和(4),可以求出从计息日开始的3个月LIBOR波动率为σ0.25=0.9171,σ0.5=0.9265。 (4)贴现率波动率的估计。由于估计贴现率选择国债市场数据为样本,因此本文使用远期历史波动率来输入利率模型。基于20支国债日报价,使用息票剥离法和三次样条插值法计算得出2014年5月12日到2014年5月26日的每日国债收益率曲线作为即期利率曲线。由于贴现率的期限是185天,所得远期利率曲线的期限也须是185天。根据公式(1),计算得出远期利率曲线(如图4)。将每日的瞬时185天远期利率波动率求平均值,计算得出的185天远期利率的历史日波动率为σ=0.791%。 图4 历史国债远期利率曲线 (5)蒙特卡罗模拟。相对于定价的0时点,决定产品收益的挂钩利率为在产品持续期内每日观察的远期利率,用F表示挂钩利率,所需求出的利率为F(4,4,94)、F(5,5,95)、...、F(188,188,278)。对这样的具有类似路径依赖性质的利率期权,蒙特卡罗模拟结果显示,所有观察日的挂钩利率都落在[0,5%]的区间内,也就是说产品可以实现4.80%的年化收益率,期末时贴现率即半年期的远期利率为3.0410%。 (二)样本产品现金流的分解与确定在定价之前,首先需要明确产品定价的时间。本文以样本产品起售日为定价的0时点。由于产品起售日至起息日之间并非投资期限,所以最终得到的产品现金流都需贴现回起息日。从结构上来看,该产品由一个以100万元为面值的零息债券和一个利率期权组成。对于固定收益部分,定价所需计算的变量则是在产品持续期185天时间的贴现率。预测产品贴现率需要预测出产品持续期内的远期利率期限结构,贴现所需利率为f(188,188,373),即期末时的185天远期利率。再来考察样本产品的期权部分,该产品的利率期权是一个奇异期权,该期权的价值由挂钩利率来确定。设产品在持续期内挂钩的3个月美元LIBOR在[0,5.00%]区间内的天数为n,产品的持续期为N(N=185)天,则由产品收益计算方法可知,期末时产品现金流I为 将估计的期权现金流以期望贴现率贴回起息日,得到利率期权产品价格P为 (三)定价结果分析根据样本产品的现金流及贴现率得出产品的理论价格,相关结果见表3。由于该产品本金数额较大,设产品本金为100元,根据这个基数计算产品价格。结果表明,此产品的理论价格为100.8871元,为本金的1.0089倍,投资者每投资100元本金在半年内实际可获得2.3961元的现金净流入。 表3 每100元本金的理论价格 由此可以看出,产品理论价值大于实际价格,该产品是折价发行的,值得投资者投资。其中,保本条款的保障本金安全,而利率期权部分也体现出了一定的盈利能力。观察产品说明中的挂钩利率和历史数据描述中3个月期美元LIBOR曲线,可以发现利率水平都处于[0,5.00%]的区间内,投资者获得最高收益的情况会比较乐观。蒙特卡罗模拟结果也印证了这一点,所有模拟出来的利率水平都低于5.00%的边界,也就意味着投资者几乎已经锁定4.80%的年化利息收入。在期末,该产品发布的收益公告显示产品达到其最大年化收益4.80%,与本文得出的实证结果相同。 另外,由于产品的发行日从2014年5月26日开始,而计息起始日为2014年5月30日,若投资者在26日投入资金,那么投资者会有4天的时间没有收益,这部分资金的闲置对于投资者来说也是一种潜在的损失。因此,购买日期越接近起息日对投资者来说面临的损失就越小,但理财产品也可能快速售完,因此不能在销售的最后一天去购买产品。 (四)产品价格的敏感性分析 (1)挂钩利率及其波动率敏感性分析。由于挂钩利率实际值比区间上限小很多,且近几年的3个月LIBOR数据没有高过1%,当挂钩利率变化不大时,它落在区间内的天数不变,而挂钩利率波动率对价格的影响也类似如此。因此,产品现金流不会变化,价格也不会变化。 (2)贴现率敏感性分析。假设其他输入变量不变,分别使贴现率的期初即期利率各上升和下降5%和10%的水平,得到的价格与基准水平的理论价格相比较。当期初贴现率水平上升时价格下降,期初贴现率水平下降时价格上升。产品理论价值变动情况见表4。 表4 价格对贴现率的敏感性分析 (3)对贴现率波动率的敏感度分析。由于计算时未能获得有效的市场数据,只运用历史波动率计算贴现率,所以需分析波动率对定价的影响。假设其他输入变量不变,分别使历史波动率上升和下降各5%和10%的水平,与基准水平下的理论价格相比较。在不同初始波动率水平下,波动率越高,产品价格越低,但整体变化幅度不大。产品理论价格变动情况见表5。 表5 价格对贴现率波动率的敏感性分析 本文构建了利率挂钩产品定价的一般模式,选择区间累积型利率挂钩产品作为样本进行案例分析。分析结果显示,样本产品是折价发行的,值得投资者投资,但该产品挂钩利率远小于设定的区间上限,在市场未发生剧烈变化时收益几乎是固定的。另外,敏感性分析显示,价格的变动与期初贴现率及波动率的变动呈负相关,二者对价格的影响程度不大。应用本文构建的定价模式,投资者可直接通过定价结果来评价产品是否值得购买以及相应的风险,发行者也可用其评估产品定价的准确性。由于我国利率市场上没有基于国债的金融衍生品,在确定贴现率波动率时使用历史波动率,而未能运用市场上衍生产品的隐含波动率作为反映市场波动率的指标。今后在我国利率市场更加完善时,将时变的波动率代入利率模型会使贴现率更加贴近市场实际。 *本文系国家社会科学基金资助项目(项目编号:15BJY036);黑龙江省自然科学基金资助项目(项目编号:G2015005);黑龙江省社会科学基金资助项目(项目编号:14B073)阶段性研究成果。 [1]成黎明:《中国债券市场中内嵌利率期权债券的定价研究》,南京航空航天大学2009年硕士学位论文。 [2]刘昭文:《触发性结构化利率债券定价的蒙特卡罗方法研究》,《经济论坛》2010年第6期。 [3]李勇飞、侯志强:《基于LMM的美式可赎回债券定价研究》,《北方工业大学学报》2013年第1期。 [4]孙学彬、潘永泉:《利率挂钩型结构化产品定价分析》,《时代经贸》2014年第6期。 [5]蒋承、郭黄斌、崔小勇:《利率衍生品的定价研究——基于LIBOR市场模型》,《金融理论与实践》2010年第2期。 [6]Boyle P.Options:A Monte Carlo Approach.Journal of Financial Economics.1977,4. [7]Boyle P,Broadie M,Glasserman P.Monte Carlo methods for security pricing.Journal of Economic Dynamics and Control. 1997,21. [8]Cox J C,Ross S A,Rubinstein M.Option pricing:A simplified approach.Journal of financial Economics.1979,7. (编辑杜昌)
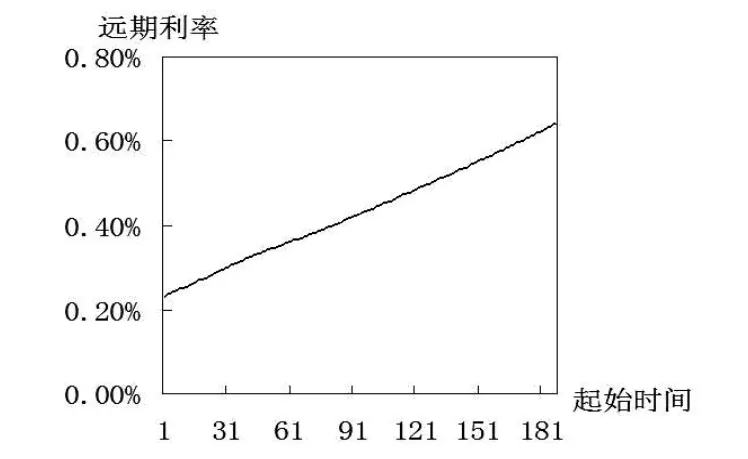
四、利率挂钩产品定价案例




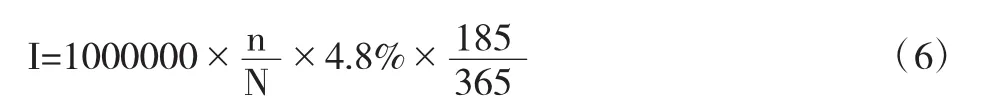
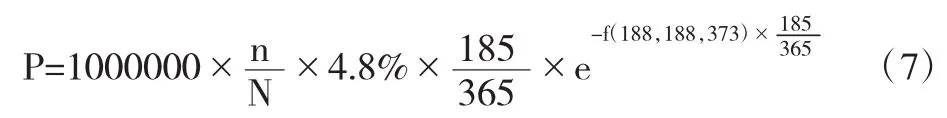



五、结论
