仿真瑞利信道的有效方式

2017-06-05黄根凯

环球市场信息导报 2017年9期

◎黄根凯

仿真瑞利信道的有效方式

◎黄根凯

本文将会在正弦的基础上对仿真瑞利信道的研究方法进行分析。在自相关的函数中，有在复随机过程中改进的方法函数，也有正交分量和同相之间的自相关函数，而且互相关函数是和理论参考值是同等的。根据仿真的结果可以看出，在复随机过程中对生成的方法进行改进，其中的相位概率密度相关的函数、复随机过程中的幅度、电平的平均通过率、衰落的平均持续时间等都具有接近理论参考值。

无线信道中关于电磁波的问题，因为受到绕射、移动台有关的运动速度、反射、散射信号的传送带宽度、环境中的物体移动速度等因素的影响，造成接收端在小范围的信号接受总是出现剧烈的波动，也可以称为是小尺度的衰落和快衰落。一般情况下，小尺度的衰落信道出现响应的包络主要是根据瑞利进行分布，它是在（-π，π ）服从内表现出的均匀分布。所以，想要建立无线信道的模型，主要就是对瑞利衰落包络的产生进行更有效的分析。

本文主要参考了Rayleigh有关的衰落信道的仿真模型内容，而且这些模型都是根据Clarke相关的信道参考模型，出现最早的Rayleigh衰落信道仿真模型是由Jakes提出来的，但是它的相关性是一个确定的函数，这一点是不能体现出信道的随机性，而且在信号的生成中还具有非平稳的广义缺点。而Zhang等人在方法的研究中对自相关的函数以及互相关的函数等进行了特性的统计，这个研究与参考模型在复数随机过程中要求相符合；但是在复数随机过程中，有关同相与正交分量之间的概率函数密度依然存在着严重的非平稳广义缺点，而且在包络平方的自相关函数中也存在着相同的问题；在自相关函数R|Y|2|Y|2（τ）中，进行包络平方的推到所得到的结果精确度不够高。而Zhang对研究方法进行改善，能够消除这些缺点，在复数随机生成的过程中，还能达到参考模型的特性统一要求。

信道的参考模型

在仿真的平台衰落信道中进行分析，主要是建立一个广义平稳的复高斯随机的过程Y（t）=Yc（t）+jY5（t）,其中正交分量YS（t）和同相的分量Y0（t）是属于状态标准的过程，而且具有线面这种统计特性：

其中，J0(°)表示的是在第一类中有关0阶的贝塞尔函数，ωd表示多普勒频移中的最大数值。

改进信道的模型

根据Zhang的模型试验优点，本文将会在他的基础上进行仿真模型的建设：

所以得出：

根据上述公式的计算结果进行分析，可以得出如果N是有限的数值，这些数值和参考模型的值是完全相等的；而其中2||2||YYR

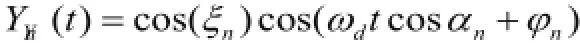
由于YC（t）构成的分量是和YS（t）的相关分量构成Ysn（t=计算的结果均是期望为零，其中方差则是1，而且这些统计是具有独立的随机过程，根据中心极限的相关定理进行计算可以得出YC（t）和YS（t），也是期望为零，逐渐接近正太分布的过程，该模型的建立将因为Ycn（t）有关的方差和时间相关性，也就是说不是常数，造成的YC（t）的概率密度中出现的非平稳性的缺陷消除了。所以|Y（t）是满足瑞利的分布的，也就

另外，由于Y（t）是属于虚部和实部中的不相关的零均值在进行复高斯随机的过程，根据以往的试验分析可以得出Y（t）相关的相位服从几乎都是均匀分布的，也就是：

根据电平平均通过率以及衰落平均持续时间，对信号衰落表现的二阶统计特征进行了分析，他们对于进行系统设计、信道建模以及系统的性能分析等因素具有非常重要的帮助。比如：

根据衰落平均的持续时间，以及电平平均通过率两个因素进行突发错误的统计特征的计算，之后在将系统的编码以及交织深度进行优化设计。

电平的平均通过率YN（r），主要是指在每秒内通过随机的过程，Y（t）由低处向高处经过的时候，产生了电平r的平均次数，根据Matthias P等人对瑞利过程中的电平通过率得出

该公式中2

0σ是属于Y（t）的方差，β则是自相关函数)(τ R当原点τ=0的时候的负曲率，也就是：

d212π2ω2β=−dτ2RYcYc(τ)|τ=0=2π,∫0(ωdcosθ)dθ=2

d衰落的平均持续时间)(rTY，是指在随机的过程中Y（t）低于电平r给定的时间相隔的长度中的数据期望。根据Matthias等人在瑞利过程中表现的平均水落持续的时间：