300 MW核电厂循环水泵部件可靠性建模分析
2017-06-01郭强蔡胜武
郭强,蔡胜武
(中核武汉核电运行技术股份有限公司,湖北武汉430223)
300 MW核电厂循环水泵部件可靠性建模分析
郭强,蔡胜武
(中核武汉核电运行技术股份有限公司,湖北武汉430223)
设备可靠性建模是核电厂概率安全分析(PSA)和维修周期优化的重要基础。以秦山300 MW核电厂循环水泵部件(叶轮)为例,针对完整数据和右截尾数据同时存在的情况,分别采用最小二乘估计和极大似然估计得到4种常见寿命分布的参数估计值,通过不同的拟合度确定最优拟合分布,并对其结果进行分析比较。结果表明极大似然估计拟合效果更佳,是核电厂设备可靠性建模的一种有效方法。
可靠性建模;数据分析;最小二乘估计;极大似然估计;拟合度
0 引言
2014年国家核安全局要求核电厂开展设备可靠性数据采集工作[1],并委托环境保护部核与辐射安全中心负责数据处理和发布[2]。可靠性建模是通过数据分析得到寿命分布模型,是概率安全分析(PSA)和维修周期优化的前提和基础,对确保我国核电厂PSA模型以及相应分析结果的准确性和合理性具有重要意义[2]。本文以秦山300 MW核电厂循环水泵(简称循泵)叶轮为例进行可靠性建模分析,为核电厂设备可靠性建模提供了有效方法和经验。
1 数据类型和分析
叶轮在其失效或泵体解体大修时进行更换,假设其更换为完美维修,相邻两次失效时间满足独立一致分布。
1.1 数据类型
在试验数据和现场数据中主要包含以下两种数据类型:完整数据和截尾数据[3]。
(1)完整数据即观察对象的寿命起止时间都已知的数据,即失效数据。
(2)截尾数据即观察对象的寿命数据不完整,可能有许多种情况,常见的有:①右截尾数据:观察对象的寿命值大于某一已知值;②左截尾数据:观察对象的寿命值小于某一已知值;③区间截尾数据:观察对象的寿命值位于某一已知的区间。由于记录不完整或未能观察到精确的失效时间,现场数据将包含许多截尾数据。截尾数据同样能反应出观察对象的部分寿命特征,也可被用于可靠性建模。
1.2 数据分析
对于完整数据和截尾数据,失效概率估计值F(t)的计算方法有所不同。
(1)完整数据的参数估计。设有n个失效数据,将它们以增序排列,并按顺序编号为1到n,即t1≤t2≤…≤ti≤…≤tn,则失效概率F(ti)可使用公式1-betainv(0.5,i,n-i+1)计算,一般采用中位秩估计失效概率F(ti)的值,近似中位秩估计公式为[4]:

(2)不完整数据的参数估计。当数据列包含截尾数据时,其参数估计比完整数据的要复杂。本文只考虑右截尾数据,根据Johnson方法[5],设数组含有n个数据,其中有m个右截尾的数据,(n-m)个失效数据,对所有数据以增序排列并用1到n编号,记这列编号为j,对所有失效数据同样按增序1到(n-m)进行编号,记这列编号为i,则第i个失效数据的失效顺序号为:

式(2)中,定义r0=0。以ri代替式(1)中的r,就可以计算得到每一个失效数据的失效概率估计值。
2 拟合分布方法
在拟合分布时,通常情况下完整数据和截尾数据会同时存在。若截尾数据的所占比例过大,则拟合分布精确度过低,没有实际意义。本文采用最小二乘估计和极大似然估计这两种常用的点估计方法进行参数估计。
2.1 最小二乘估计
最小二乘法是点估计的一种方法,它主要用来估计线性函数(常称为线性回归)的未知参数。由最小二乘法求得的参数估计,称为最小二乘估计[3]。
在x-y直角坐标系中,根据观测到的n个失效数据{xi,yi},i=1,2,…,n,按要求配出一条直线

使得该直线与各个点{xi,yi},i=1,2,…,n的偏差平方和达到最小,这就是最小二乘的基本思想。
回归直线式(3)与各观测值的垂直偏差记为,以代表垂直偏差平方和,用数学公式可表示为

因此,能够代表x与y线性关系的回归直线,就是所有直线中使E达到最小的那一条,也就是方程y=a+bx中系数a和b使E达最小值的那个方程所对应的直线。
2.2 极大似然估计
极大似然估计是一种重要的估计方法。它的基本思想是:由于样本来自于总体,因此样本在一定程度上能够反映总体特征。如果总体的待估参数为θ,在θ的一切可能值中,选取一个使样本观测值结果出现的概率达到最大的值作为的θ估计值,记为θˆ,这就是极大似然估计[3]。
设有一列不完整数据,共n个。失效数据为nf个,及其集合为F;右截尾数据为nc个,记其集合为C。记参数为θ,则其似然函数L(θ)为:
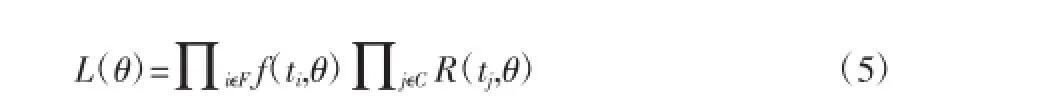


式(6)中ln[L(θ)]为对数似然函数。
3 拟合度计算
拟合度是指回归直线对观测值的拟合程度。度量拟合度的统计量是可决系数r2,其计算公式为[6]:

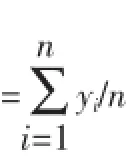

4种常用分布为指数分布、威布尔分布、正态分布和对数正态分布,本文以威布尔分布为例,将分布模型线性化。
威布尔分布的累积分布函数为

公式两边取自然对数,得

继续两边取对数,得

根据式(3)可得

于是,式(7)中

4 循泵叶轮可靠性建模
4.1 数据收集
循泵系统有6台循泵并联安装,其功能主要是抽取海水为汽轮机凝汽器提供冷却水,正常工况下,仅需部分循泵运行即可满足冷却水需求,因此循泵系统属于k/n表决系统。在秦山300 MW核电厂收集到的循泵叶轮的数据为累计运行时间(单位为d),増序排列整理后的结果10.22+,406.89,544.12+,49.44+,413.89,566.02,51.79,463.29,602.07,259.12+,469.37,604.44+,348.30,509.07,687.92,360.90+,516.04+,930.51,其中包含了失效数据和右截尾数据,+表示数据为右截尾数据。
4.2 参数估计和拟合度计算
根据叶轮累积运行时间数据和最小二乘估计方法,可以得到循泵叶轮的4种常见寿命分布的参数估计,并通过拟合度计算得到各分布的拟合度(表1),拟合分布曲线见图1。从表1可知,正态分布的拟合度最接近1,为0.93,说明最小二乘估计得到的最优拟合分布为正态分布。在图1中,也可看出正态分布拟合效果最佳。

表1 最小二乘估计和拟合度
根据叶轮累积运行时间数据和极大似然估计方法,得到的4种常见寿命分布的参数估计和拟合度(可决系数r2)见表2,拟合分布曲线见图2。
从表2可知,极大似然估计得到的拟合分布的拟合度都不理想,说明极大似然估计容易出现噪点(例如威布尔分布线性变换后的第一个点,见图3)。这是由极大似然估计的定义决定的,其拟合分布尽可能靠近大部分的较集中的观测点,从而会远离个别观测点(噪点)。而根据最小二乘估计的定义,其拟合分布离每个观测点距离相对平均一些。因此,可决系数r2可作为衡量最小二乘估计的拟合效果的拟合度,但不适合极大似然估计。
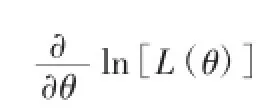

图1 最小二乘估计的拟合分布曲线
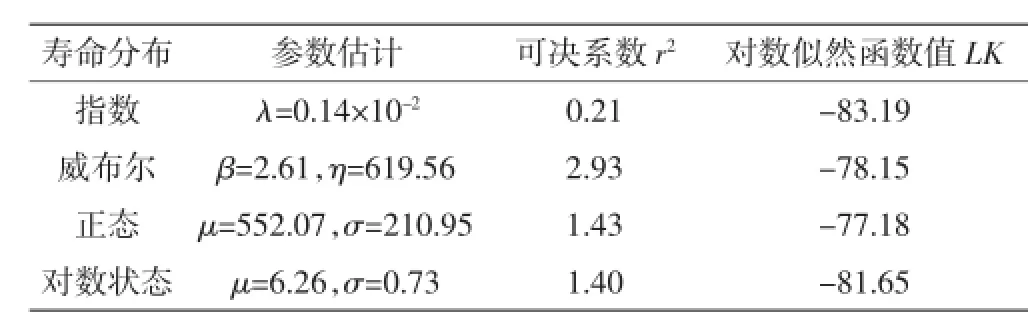
表2 极大似然估计和拟合度
4.3 结果对比分析
根据式(5)和(6),求得最小二乘估计所得拟合分布的对数似然函数值LK分别为-83.28(指数分布)、-81.15(威布尔分布)、-77.65(正态分布)、-82.85(对数正态分布),其拟合度排序与可决系数r2的一致,说明LK也可作为最小二乘估计的拟合度度量。
由于-77.65(正态分布)小于-77.18(见表2的正态分布),因此两种方法得到的正态分布拟合效果相近,而极大似然估计的拟合效果更佳。在图4中,也可看到相同的结果。
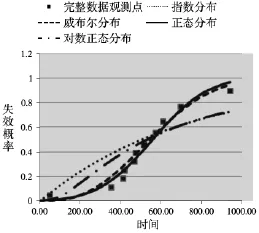
图2 极大似然估计的拟合分布曲线
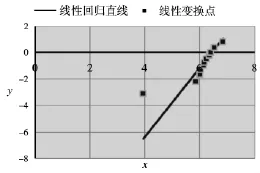
图3 威布尔分布的线性回归
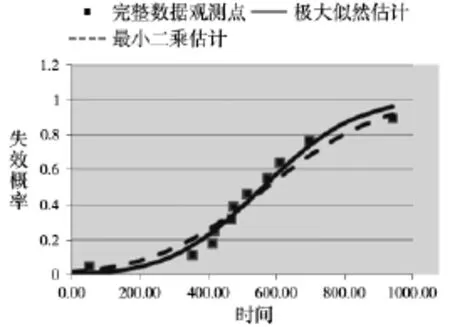
图4 最小二乘估计和极大似然估计的正态分布
5 结论
针对循泵叶轮的完整数据和右截尾数据,采用最小二乘估计、极大似然估计以及拟合度计算,对循泵叶轮进行了可靠性建模,得到了最优寿命分布模型。结果表明:
(1)通过最小二乘估计和极大似然估计所得拟合分布结果的比较分析可知,在截尾数据存在的情况下,极大似然估计拟合效果更佳,是核电厂设备可靠性建模的一种有效方法。
(2)对数似然函数值LK可作为最小二乘估计和极大似然估计两种方法的拟合度度量,而可决系数r2适合于最小二乘估计,但不适合于极大似然估计。
[1]国家核安全局.核电厂设备可靠性数据采集(试行)[R].国家核安全局,2013.
[2]国家核安全局.中国核电厂设备可靠性数据报告(2015版)[R].国家核安全局,2015.
[3]赵宇.可靠性数据分析[M].北京:国防工业出版社,2011.
[4]Nelson Wayne.Accelerated Testing:Statistical Models,Test Plans,and Data Analysis[M].New York:John Wiley&Sons,1990.
[5]蒋仁言,左明健.可靠性模型与应用[M].北京:机械工业出版社,1999.
[6]吴世农.高级管理统计方法[M].北京:中国对外经济贸易出版社,1997.
〔编辑 凌瑞〕
TM623.7
B
10.16621/j.cnki.issn1001-0599.2017.01.15
