高等数学指导中学数学在函数思想上的体现
2017-06-01赵丽丽
赵丽丽
(赤峰学院 计算机与信息工程学院,内蒙古 赤峰 024000)
高等数学指导中学数学在函数思想上的体现
赵丽丽
(赤峰学院 计算机与信息工程学院,内蒙古 赤峰 024000)
作为一名优秀的教师,只具备高中数学所涉及的知识,那是远远不够的,为了能更好的理解和渗透中学数学的教材,这就要求中学数学教师利用高等数学指导中学数学,用高等数学的思想方法、理论依据一眼看穿中学数学,结合中学数学的实际,运用中学生可以接受的方法来指导中学数学的教学与解题.从中学数学与《数学分析》教材的分析来看,函数部分所占比例较大,可以说函数思想像一双无形的手拉近了高等数学与中学数学的距离,润物细无声般的将中学数学推向高等数学.
数学思想;函数思想;问题
《数学分析》的研究对象是函数,具体内容包括:一元函数的极限,一元函数微积分,实数的连续性,无穷级数与含参变量积分,多元函数微积分等.中学数学的主要内容:集合与简易逻辑,函数,数列,三角函数,平面向量,不等式,极限,导数,复数,排列、组合、二项式定理,概率统计以及解析几何部分,这些问题属于《数学分析》,《概率统计》,《解析几何》等数学分支,但在教材更多的是讲述办法,理论上的叙述要求的不是十分严谨,但是对更好的理解和渗透中学数学教材,这就要求中学数学教师利用高等数学指导中学数学,用高等数学的思想方法、理论依据一眼看穿中学数学,结合中学数学的实际,运用中学生可以接受的方法来指导中学数学的教学与解题.
从中学数学与《数学分析》教材的分析来看,函数部分所占比例较大,可以说函数思想像一双无形的手拉近了高等数学与中学数学的距离,润物细无声般的将中学数学推向高等数学.
我们曾都有过这样的困惑:题目讲的很多,但是学生都是在模仿解题,老师只要稍一改变则不知所措,究其原因在于学习中仅仅就题论题,见子打子,并没有真正领会隐含与数学问题探索中的数学思想方法.新课标强调教师在教学中授之以“渔”比授之以“鱼”更为重要;即要使学生掌握数学思想方法方面的知识,逐步形成用数学思想方法指导思维活动,这样在遇到同类问题时才能从容对待.
所谓数学思想方法是处理数学问题的指导思想和基本策略,是数学的灵魂.数学思想和数学方法是紧密联系的.一般来说,强调指导思想时称为数学思想,强调操作过程时称为数学方法.而中学数学中的基本数学思想如下:两大“基石”思想:符号化与变元表示(换元思想、方程思想、参数思想)与集合思想(分类思想、交集思想、补集思想)两大“支柱”思想:对应思想(函数思想、变换思想、递归思想、数形结合思想)与公理化与结构思想(公理化思想、结构思想、极限思想)两大“主梁”思想:系统与统计思想(整体思想、分解组合思想、运动变化思想、最优化思想)与化归与辨证思想(纵向化归、横向化归、同向化归、逆向化归思想,对立统一,万变,一分为二思想).
在上述诸多思想中,函数思想在初、高等数学,在自然科学和社会科学中均有着广泛的应用,起着“基础”和“纽带”的作用,是处理常量数学和变量数学的重要思想,在解决一般数学问题中具有重大的方法论意义.同时函数把数学的各个分支紧紧连在一起,函数与方程、不等式、数列、几何、三角等彼此渗透,相互融合,构成了函数应用的广泛性、解法的多样性、思维的创造性.又由于函数充分体现了集合、对应、映射等基本数学思想,因而就是中学数学能接近现代数学的科学水平,并且是学生从中获得基本的、深刻的、有用的高等数学思想方法.总之,函数描述了自然界中量的依存关系;反映了一个事物随另一个事物变化的关系和规律.函数思想即是用联系变化的观点,建立各种变量间的依存(函数)关系,通过函数形式并利用函数的有关性质和方法达到解题目标的策略,函数思想是一种解题观念,其运用范围并不局限于函数问题,它贯穿与整个高中数学.
1 在概念教学中渗透函数思想
数列是函数,是一种特殊的函数,因此许多问题可以用函数的观点来研究如:数列概念,求解等差数列中的a,an,sn, n,d等.
2 在定理和公式中渗透函数思想
例 等差数列通项公式an=a1+(n-1)d中an是n的一次函数;前n项和公式中sn是n的二次函数.
3 在问题解决中渗透函数思想
3.1 实际问题
例 某工厂要修建一个圆形喷水池,在水池中央垂直于水面处安装一个柱子0A,0下号在水面中心处,OA= 1.25m,安装在柱子顶端A处的喷头向四周喷水,水流沿着形状相同的抛物线路径向四周落下,并在过0A的任意平面上抛物线如图(1),为了使水流的形状更漂亮,要使水流在到OA距离为1m处达到距水面最大的高度2.25m,不收其他因素影响,水池的半径要多少米,才能使喷出的水流不落在水池外面.
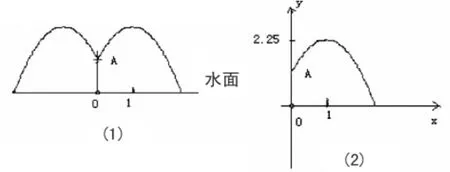
分析:我们的解题思路是:实际问题→数学问题→代数问题→函数问题→函数问题的解→实际问题的解.
如图(2)建立直角坐标系:则水流显现的抛物线方程为y=a(x-1)2+2.25,由题意:点A的坐标为(0,1.25),
把x=0,y=1.25代入上述方程 得a=-1
于是 抛物线方程为y=-(x-1)2+2.25
令y=0 得(x-1)2+2.25=0
解得x1=2.5,x2=-0.5(不合题意舍去)
所以x=2.5
答:水池半径至少要2.5米才能使水流不致落到池外.
3.2 几何问题
在几何问题中我们往往会遇到求夹角和最大(小)值和线段的最短(长)距离等问题.如果仅从集几何方面去思考,往往使问题难以解决,倘若能够灵活的应用构造函数的方法,就会使几何问题柳暗花明.
解 利用导数的几何意义:光滑曲线切线的斜率.
则过椭圆上一点(x0,y0)的切线方程为

因此本题归结为:当x,y满足(1)时
3.3 不等式问题
由于不等式有广泛的应用又是高等数学的基础,所以在高考中一直是重点考察的内容,在综合解题过程中处处分布着不等式的知识、方法与技巧.下面将从高等数学的函数思想方面研究不等式.
3.3.1 利用函数单调性
基本思想:若f'(x)≥0(f'(x)>0)则x1<x2时,有f(x1)≤f(x2)(f (x1)<f(x2)),由此可获得不等式.
例 设e是自然对数的底,π是圆周率,证明:eπ>πe.
由于x>e时f'(x)<0于是f(x)在[e,+∞)上递减故f(e)>f(π)此即(1)成立.
3.3.2 利用微分中值定理
基本思想:若f(x)在[a,b]上连续,在(a,b)内可导,则f(x)=f(a)+f'(ξ)(x-a)(ξ∈(a,b))
故当f(a)=0;(a,b)内f'(x)>0时,有f(x)>0(∀x∈(a,b]).
法1:令f(x)=x-ln(1+x)则f(x)在[0,x]上连续,在(0,x)内可导,所以有f(x)=f(0)+f'(ξ)x(ξ∈(0,x))
法3:分析:∵x>0
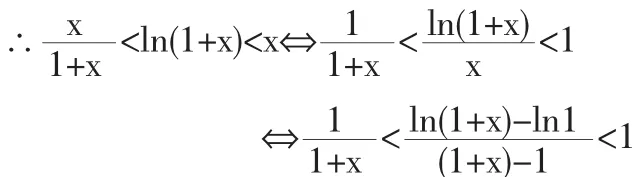
因此可利用拉格朗日中值定理
证 令f(t)=lnt,当x>0时,显然它在[1,1+x]满足拉格朗日中值定理的条件,
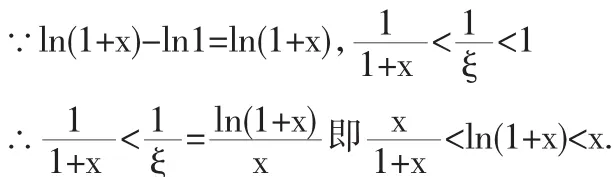
3.3.3 利用函数极值
证明 原不等式等价于(1-x)ex≤1
设f(x)=(1-x)ex,x∈(-∞,1)由f'(x)=-xex=0,得唯一驻点x=0,
又当x<0时f'(x)>0;
x>0时,f'(x)<0
故f(x)在x=0取极大值(即最大值):f(0)=1因此对所有x∈(-∞,1),都有f(x)=(1-x)ex≤1.
例2 证明t≥1,s≥0时下面的不等式成立
ts≤tlnt-t+es
证 我们只要证明函数φ(s,t)=tlnt-t+es-ts
在D={(s,t):s≥0,t≥1}上有最小值0,固定t≥1,
令φ's(s,t)=es-t=0 得s=lnt(即t=es)且
当0≤s<lnt时φ's(s,t)<0
当s>lnt时φ's(s,t)>0
可见φ(s,t)的最小值只能在曲线t=es上达到.但
φ(s,es)=ess-es+es-ess故在D上φ(s,t)≥0即有ts≤tlnt-t+es
3.3.4 利用二次函数判别式

3.4 等式、方程问题
函数通常我们用记号y=f(x)来表示变量y是变量x的函数,即“变量y通过f函数依赖于x”至于变量x取何值时,y值为零呢?于是我们引入记号f(x)=0,这就是我们常说的方程.因此,我们可以利用函数本身的性质来解决方程中的一些问题.
证x在(0,+∞)内变化即看是否存在x1,x2使f(x1)=0,f(x2) =0即问题变成证明f(x)在(0,+∞)内至少有两个零点.
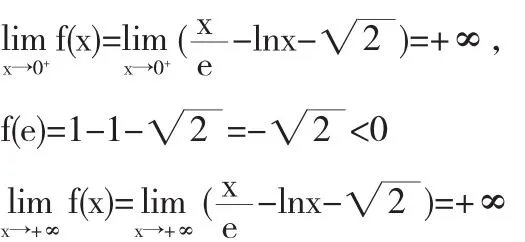
由界值定理知f(x)在(0,e)和(e,+∞)内各至少有一个零点,即方程
在(0,+∞)内至少有两个实根.
例 2 若(1+x+x2+x3)5(1-x+x2-x3)5=a30+a29x+…+a1x29+a0x30求a15.
分析:观察等式的特殊结构,可以运用函数的奇偶性.
解 构造函数f(x)=(1+x+x2+x3)5
则f(-x)=(1-x+x2-x3)5
令F(x)=(1+x+x2+x3)5(1-x+x2-x3)5
则F(x)=f(x)f(-x)
显然F(x)是偶函数.
而且观察正系数多项式F(x)展开式中系数的特征:所有奇次项系数均为零,可知F(x)=a30+a28x2+…+a2x28+a0x30
即a15=0
3.5 复数与角的问题
有关复数x+yi的辐角和模的范围问题常与正、余弦函数或实变量x,y联系在一起,可利用变量的函数来求解.
例1 已知辐角分别为θ1,θ2的复数z1,z2,满足条件:z1+z2=5i,|z1z2|=14,求cos(θ1-θ2)的最大值及最小值,并求取最小值时的z1,z2的值.
分析:这是一个最值问题,解最值问题的一般方法是要找到有关一个变量的函数,本题中的变量有θ1,θ2,还有z1,z2的模r1,r2共4个,从已知条件可以获得3个等式,其中z1+z2=5i可得两个等式,再加|z1z2|=14,寻找它们与所求结论cos(θ1-θ2)之间的关系.
解 设z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2)由题意得:

将(1),(2)两边平方代入(3)得:
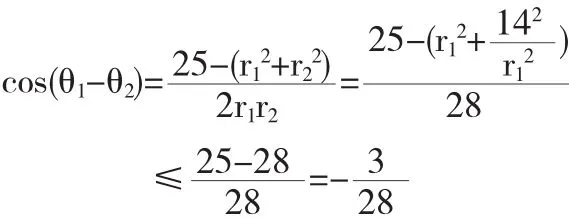
所以cos(θ1-θ2)的最大值是,最小值是-1
且当cos(θ1-θ2)=-1时θ1-θ2=(2k+1)π
例2 设复数z=3cosθ+i2sinθ,求函数y=θ-argz.(0<θ<的最大值以及对应θ的值.
分析:所求是两个动态角之间的函数最大值,而求一个角的最大(小)值,一般要转化成求这个角的某一个三角函数的最大(小)值,为了便于运算取正切,先求tgy的最大值,进而利用正切函数的单调性,求出y的最大值以及对应的θ的值.
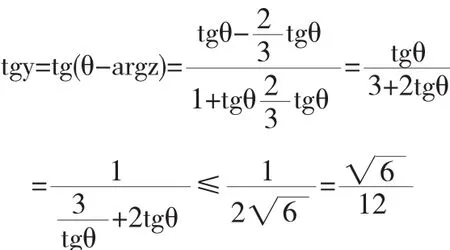
即时上式取等号.
总之应用函数的有关知识和思想解题不止以上几类,“管中窥豹,可见一斑”,它们反映了这样一种解题策略:将静止的问题放到一个更加波澜壮阔的动态过程中去考察,将局部的问题置于更加高瞻远瞩的全局上去解决.
〔1〕胡炳生,等.现代数学观点下的中学数学[M].北京:高等教育出版社,1999.
〔2〕余元希,等.初等代数研究(下册)[M].北京:高等教育出版社,1988.3.
〔3〕王后雄.十年高考两年模拟试题分类全解:数学[M].辽宁教育出版社,2006.
〔4〕裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2006.
O174
:A
:1673-260X(2017)05-0010-03
2017-01-05
