Investigation of droplet breakup in liquid-liquid dispersions by CFDPBM simulations:The influence of the surfactant type

Dongyue Li,Antonio Buffo ,Wioletta Podgórska ,Daniele L.Marchisio ,Zhengming Gao ,*

1 State Key Laboratory of Chemical Resource Engineering,School of Chemical Engineering,Beijing University of Chemical Technology,Beijing 100029,China

2 Aalto University,Department of Biotechnology and Chemical Technology,Espoo,Finland

3 Faculty of Chemical and Process Engineering,Warsaw University of Technology,Warsaw,Poland

4 Institute of Chemical Engineering,Department of Applied Science and Technology,Politecnico di Torino,Torino,Italy

1.Introduction

Immiscible liquid-liquid systems are found extensively throughout the chemical,petroleum,and pharmaceutical industries.Thanks to the increasing computational power,the flow can now be modeled by computational fluid dynamics(CFD),while the droplet size distribution(DSD)can be predicted by CFD coupled with a population balance model(PBM)[1-4].Many methods have been developed to solve the PBM,such as the classes method(CM)[5],the Monte Carlo method(MCM)[6-9],the Quadrature Method of Moments(QMOM)[10],the Direct Quadrature Method of Moments(DQMOM)[11],the Adaptive Direct Quadrature Method of Moments(ADQMOM)[12],Taylor-series Expansion Method of Moments(TEMOM)[13],and the Extended Quadrature Method of Moment(EQMOM)[14].These methods have been employed extensively to investigate different industrial processes[15-25].

One major problem in the development of PBM community is the availability of reliable sub-models for describing the different phenomena involved,notably the kernels for coalescence and breakage.Coulaloglou and Tavlarides[26]developed the first breakup kernel which is applicable for liquid-liquid dispersions in stirred tanks.They assumed that the breakup frequency of droplets can be expressed as the product of the inverse of breakup time and the fraction of the total number of breaking droplets.Konnoet al.[27]studied the breakup process in geometrically similar tanks,varying the tank diameter and the impeller-to-tank diameter ratio.They considered the breakup region in the tank as composed of two regions:one with non-isotropic turbulence and the other with isotropic turbulence.Luo and Svendsen[28]proposed a theoretical model for the breakup frequency based on the kinetic gas theory.This model does not include any unknown or empirical parameter.However,this model is found to be sensitive to integration limits[29].The importance of the influence of the intermittent character of turbulence on short duration processes,such as breakup,was underlined by Bałdyga and Bourne[30]and this effect was later included in the multifractal breakup kernels by Bałdyga and Podgórska[31].Martínez-Bazánet al.[32]investigated the breakup of air bubbles in a water jet.They postulated that the acceleration of the bubble or droplet interface during deformation is proportional to the difference between the deformation and confinement forces[33].Lehr and Mewes[34,35]and Lehretal.[36]introduced the so called capillary constraint.They assumed that before breakup the bubble is locally nearly cylindrical and they determined the diameter of smaller drops from the balance between dynamic pressure of an eddy and the capillary pressure of bubbles.Wanget al.[29]used both criteria in their bubble/droplet breakup model.The advantage of such model is that the daughter size distribution is provided directly with no adjustable parameters.However,there is a triple integralin the resulting kernel;itis therefore computationally expensive.This problem is fixed by an efficient numerical algorithm to calculate the triple integral by introducing a cutoff energy arbitrarily and calculating the probability recursively instead of using the integral[37].In the recent few years several groups of researchers focused also on the influence of energy spectrum distribution on vortex number density[38]and drop breakup in turbulent flow.Hanet al.[39]developed a mathematical model for multiple breakup(i.e.,mainly binary,ternary,and quaternary breakups)based on the theories of isotropic turbulence.Consecutively,Han and coworkers[40]developed a novel breakup kernel model in terms of the general energy spectrum function.Similarly,in order not to confine the analysis to the inertial subrange of turbulence,Solsvik and Jakobsen[41]developed the collision function and breakup kernels for complete energy spectrum of isotropic turbulence(e.g.,the energy-containing,inertial,and dissipation subranges)and for a larger range of integral scale Reynolds numbers.In the latest several years,breakup kernels which are suitable for the full range of scales of isotropic turbulence are investigated heavily[39-41].

This short review shows that after the pioneering work of Coulaloglou and Tavlarides[26],many different breakup kernels were developed and most of the studies on droplet breakup in stirred tanks are devoted to pure liquid-liquid systems.However,if the surfactant is dissolved in the continuous phase,it can decrease the interfacial tension,Hamaker constant value,as well as the mobility of drop interfaces due to Marangoni effect.Meanwhile,surfactant affects also droplet breakup[42,43].The influence of surfactant on droplet breakup can be interpreted through the decrease of interfacial tension and therefore the decrease of shape-restoring stress.Koshyet al.[44]pointed out that the maximum stable drop size can be significantly over-predicted.They observed thatdroplets in systems characterized by the same interfacial tension(one pure,the other one containing the surfactant)differ in size.Production of smaller droplets in the second case was attributed to surfactant removalfrom the surface.It was postulated that the difference between dynamic(fort=0)and static interfacial tension can aid the turbulent stress to break the droplets[44].Based on Koshyet al.'s work[44],Bąk and Podgórska[42]extended the multifractal(MF)kernel to justify this mechanism.The extended MF breakup kernel was proven to be accurate by their experimental data and their singlecirculation-loop plug flow model.

In this study, five different breakup kernels from the literature,namely Coulaloglou and Tavlarides[26](CT)breakup kernel,Bałdyga and Podgórska[31]multifractal(MF)breakup kernel and its modification by Bąk and Podgórska[42],Alopaeuset al.[45]breakup kernel,Martínez-Bazánet al.[32](MB)breakup kernel and Lehret al.[36]breakup kernel,are adopted in three-dimensional CFD simulations to investigate their ability to predictthe time evolution of the mean Sauter diameter,when different surfactants are added into the liquid-liquid dispersion.The effectof the surfactant type on breakup has not been investigated in our previous work,which focused on pure liquid-liquid dispersions[46,47],on the effect of electrostatic forces on coalescence[48]and on the validity of simplified models[49,50].The PBM is in this work solved with our implementation of QMOM in the compressibleTwoPhaseEulerFoam solver of OpenFOAM v.2.2.x[51,52].Model predictions are validated against experimental data for six different test cases(two groups),namely a stirred tank with different kinds of surfactants at different concentrations working at different stirrer speeds.In the first test group,the surfactant is Tween 20(1227.72 g·mol-1;MERCK).This surfactant can desorb during drop deformation,giving rise to additional disruptive stress.In this case the dynamic interfacial tension should be considered[42].In the second test group,the surfactant is polyvinyl alcohol with a degree of hydrolysis equal to 88%(PVA 88%,molecular weight 13000-23000,Sigma-Aldrich),which is strongly grafted to the surface,therefore,the additional stress is not generated[43].

2.Governing Equations and Population Balance Model

2.1.Two- fluid model

In the TFM both phases are described in terms of their volume fractions and average velocities and treated as continuum inter-penetrating phases governed by a continuity equation for the volume fraction of the disperse phase:

where αdis the volume fraction of the disperse phase,ρdis its density and Udis its average velocity.The volume fraction of the continuous phase αcis generally calculated by knowing that volume fractions sum to unity(αd+αc=1).The average velocity of the disperse phase(Ud)is calculated by solving the corresponding momentum balance equation:

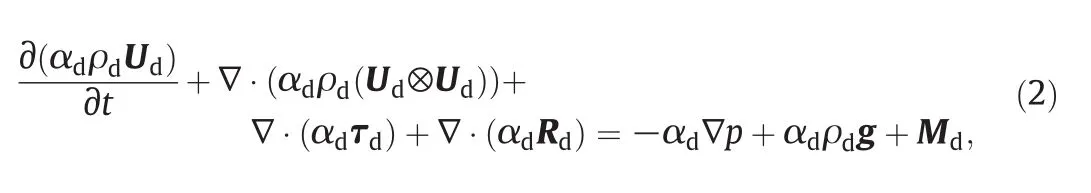
wherepis the pressure shared by the two phases[53,54],τdis the viscous-stresstensors,Rdis the Reynolds-stress tensors,g is the gravitational acceleration vector and Mdis the interfacial force term which describes the momentum exchange between the two phases and here only the drag force is taken into account[55],the drag coefficient correlation of Schiller and Naumann[56]is employed in this work;a similar equation is solved also for the continuous phase(not reported here for the sake of brevity).The Reynolds-stress tensors for the disperse phase(and similarly for the continuous phase)can be modeled by using the well-known Boussinesq approximation.

Different turbulent models can be employed to calculate the turbulent term in the momentum equations.Standardk-ε model is one of the most popular turbulent models in multiphase simulation for its good trade-off between accuracy and reasonable computational cost[55,57,58,51,46].The drawback of the standardk-ε model is that the turbulence dissipation rate is often underestimated[59,45,60,46].This underestimation poses a serious problem to breakage kernels which depend largely on the turbulent dissipation rate.However,this underestimation can be overcome by a simple correction for the turbulent dissipation rate[61,46]and it was employed in our previous research[46].In the standardk-ε model,the turbulent kinetic energy,k,and the turbulent energy dissipation rate,ε,are obtained by solving two additional conservation equations,defined as follows:where νt=Cμk2/ε is the turbulent viscosity andCμ,σk,σε,C1,andC2are model constants and whereGkrepresents the production of the turbulent kinetic energy.

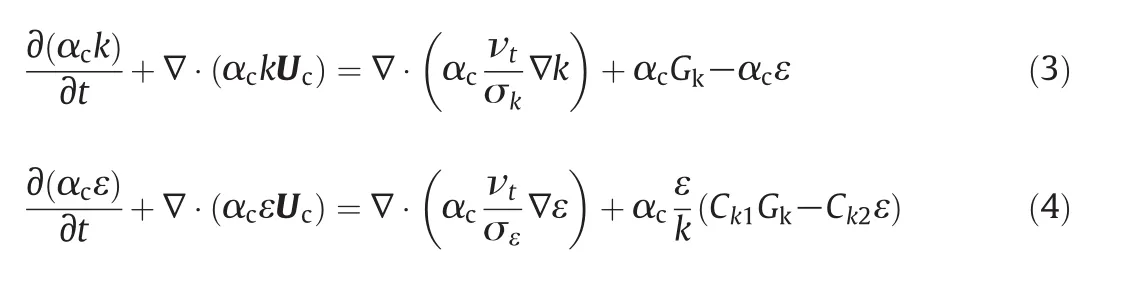
2.2.Population balance model

The PBM for the investigated liquid-liquid system is mainly constituted by a population balance equation(PBE)accounting for the birth and death of droplets due to breakup.Due to the low volume fraction of the disperse phase(5%for all the test cases)and mainly to the presence of surfactant,coalescence is neglected in this work,and only breakup is considered,as done in other similar works[62,63,64,46].The PBE that governs the evolution of the DSD reads as follows(omitting space and time dependencies)[61]:

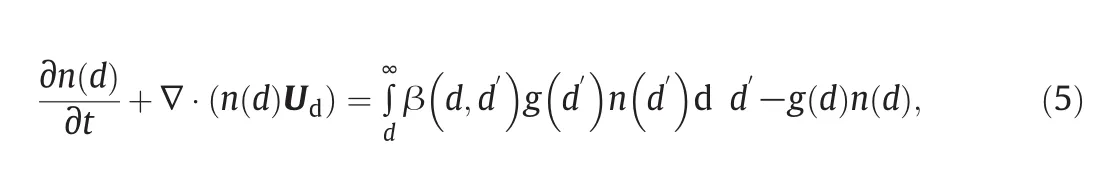
wheren(d)is the DSD anddis the droplet size,gis the breakup kernel(or frequency of breakup)and β(d,d′)is the daughter size distribution function stating the size distribution of daughter droplets originating from a mother droplet of sized′.More details about Eq.(5)can be found in the book by Ramkrishna[65].

QBMM can be used to solve the PBE.The general idea behind QMOM is to approximate the unknown DSD,n(d),by a summation of Dirac delta functions[66]centered on the nodes of a quadrature approximation:

wherewαanddαare theNweights and nodes(or abscissas)of the quadrature approximation of orderN.TheNnodes and weights are calculated in QMOM from the first 2Nmoments of the DSD:

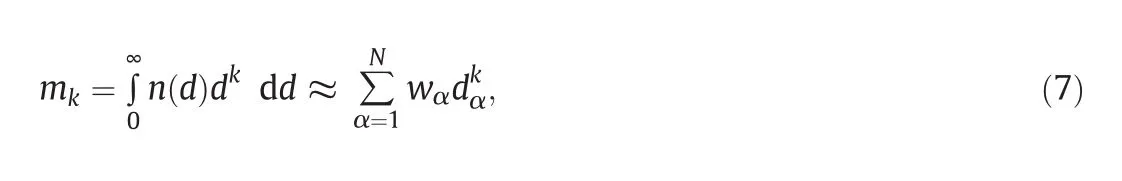
withk∈0,…,2N-1,by using the so-called moment inversion algorithms,such as for example the Product-Difference or Wheeler algorithms as illustrated in the book by Marchisio and Fox[67].By applying QMOM the transport equation for the moment of orderkbecomes:

where the integral appearing on the right-hand side is often solved analytically(if the functional form of β allows it).

As it can be seen from Eq.(8)the calculation of the DSD requires knowledge of the size of the droplets that are formed during the breakup process,contained in the so-called daughter distribution function:β(d,d′).Models for daughter distribution function can be classified as phenomenological and statistical.Phenomenological models are usually based on the change of surface energy.Other constraints can be also taken into account resulting in different shapes of β(d,d′):Bell-shape[68],U-shape[69,28]and M-shape[36,29].In statistical models,it is assumed that the size of daughter droplet is a random variable and its probability distribution satisfies a simple equation.Adetailed discussion on the different daughter distribution functions can be found in works by Lasheraset al.[33]and Liao and Lucas[70].Based on a common statisticaldistribution,Laakkonen[71]proposed a daughter distribution function as follows:

It assumes that two droplets of different sizes are formed in the breakup process and that symmetric breakup is the most likely event which is consistent with Coulaloglou and Tavlarides[26],owing to the droplet redistribution mechanism caused by the external stresses,as described in detail by Andersson and Andersson[72].In this work,the daughter distribution function reported in Eq.(9)is adopted as of it avoids heavy numerical calculations and it can provide similar results with other forms.

When Eq.(9)is substituted into Eq.(8)an analytical solution exists for the term in between squared brackets(fork≥0):

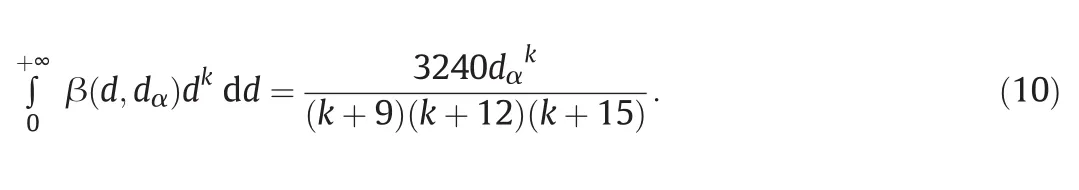
3.Breakup Kernels

The breakup of droplets in turbulent dispersions is influenced by the continuous phase hydrodynamics and interfacial interactions.Generally,the breakup mechanism can be expressed as a balance between external stresses from the continuous phase,which attempt to destroy the droplets,and the interfacial tension plus the viscous stress of the fluid inside it,which restores its form.This balance leads to a maximum stable particle diameter.Therefore,the breakup of a droplet is determined by the hydrodynamic conditions in the surrounding liquid and its characteristics.Different breakup kernels have been proposed to describe droplet and bubble breakup.In this work the breakup kernels of Coulaloglou and Tavlarides[26](CT),Alopaeuset al.[45](Alopaeus),Martínez-Bazánet al.[32](MB),Lehret al.[36](Lehr)and Bałdyga and Podgórska[31](MF)were investigated.The basic theory behind these breakup kernels are discussed in what follows.

3.1.CT breakup kernel

A pioneering phenomenological kernel was developed by Coulaloglou and Tavlarides[26]for liquid-liquid dispersions in turbulent flow.They assumed that droplet oscillates and deforms due to local pressure fluctuations.Moreover,it is assumed that the oscillating droplet will break if the transmitted kinetic energy is higher than the surface energy[73].The breakup kernel reads as follows:

where ε is the turbulent energy dissipation rate,dis the droplet diameter,ρcis the density of the continuous phase and σ is the interfacial tension.C1andC2are dimensionless constants that are typically obtained by fitting with experimental data.When the global hold-up of the dispersed phase is moderate(e.g.,larger than 10%),a turbulent dampening factor should be included in the breakup kernel which is reported by the following expression:

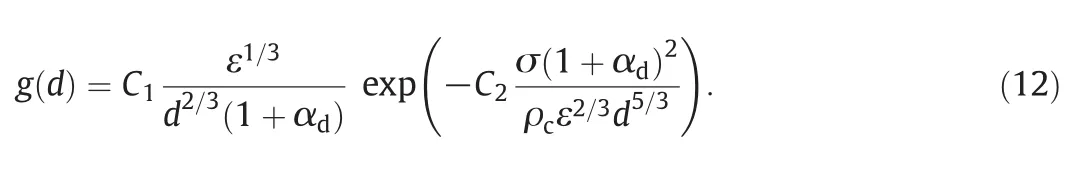
In the literatureC1andC2are suggested to be 0.00481 and 0.08[70];these values were also confirmed in our previous work[46]and are adopted also here.

3.2.Alopaeus breakup kernel

The Alopaeus breakup kernel is based on the breakup kernel developed by Narsimhanet al.[74],where a stochastic model for the prediction of the breakup frequency is proposed,if the density and viscosity of the disperse phase are similar to those of the continuous phase.In their work,eddy-drop collisions are assumed to form a Poisson process.Then,by using probability theory,the following function was proposed:

whereC1=0.883 was obtained under the incorrect assumption that the minimum increase of surface energy is when the parent droplet is broken into two equally-sized daughter droplets.Alopaeuset al.[45]proposed thatC1should be smaller than 0.883.Moreover,they included an ε-dependency for the eddy-drop collision frequency and took into account that breakup can be controlled not only by surface forces,but also by viscous ones.Their breakup kernel takes the following form:

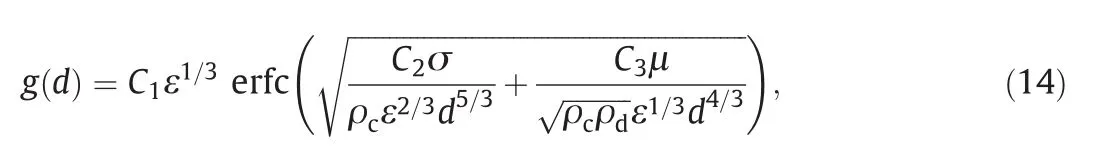
whereC2andC3are dimensionless constants,whileC1is dimensional.The effect of the two confining forces depends on the magnitudes of the interfacial tension and the viscosity of the disperse phase[45].

In the Alopaeus breakup kernel,differentvalues ofC1,C2andC3have been chosen depending on the model in use.For example,when the PBM was solved with a single block model:C1=0.986,C2=0.000892 andC3=0.2[45],while with a multiblock model:C1=3.68,C2=0.000775 andC3=0.2[45].It had been proven in many other literature sources that different values can be chosen for these constants depending on the mixing system[63,75,76].In this work,the originalC1=3.68 andC3=0.2 from Alopaeuset al.were adopted[45],whileC2was instead fitted with the experimental data and it is taken equal to 0.0775.

3.3.MB breakup kernel

Martínez-Bazánet al.[32]breakup kernel is derived from experiments of breakup of air bubbles of known diameters injected into a fully developed turbulent water flow for very high turbulence energy dissipation rate.MB breakup kernel's premises are radically different from those used in the CT breakup kernel.It assumes that the breakup frequency is proportional to the difference between the inertial stresses which produce the bubble deformation and confinement ones caused by surface tension.It is reported to be formulated as follows:

whereC1=0.25 andC2=8.2[32].C1was found experimentally,whereasC2is the Kolmogorov parameter in the structure function correlation and it was given by Batchelor to be equal to 8.2[77].Moreover,in this kernel,a critical diameterdc=1.26(σ/ρc)3/5ε-2/5is introduced and for droplets smaller than the critical diameter is assumed to be zero.

3.4.Lehr breakup kernel

Lehret al.[36]developed their breakup kernel to predict the bubble size distribution in turbulent bubble columns with high superficial gas velocities.The authors assumed that the breakup of a bubble is determined by the balance between the interfacial force of the bubble surface and the inertial force of the colliding eddy.Only eddies with length scales smaller than the bubble diameters were considered as capable to induce breakup.The Lehr breakup kernel is reported as follows[36,70]:

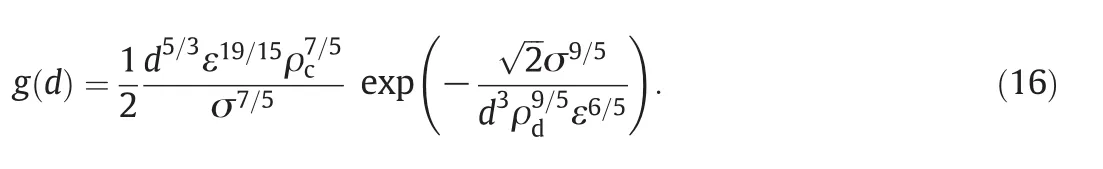
As may be seen no empirical parameters to be fitted with experimental data are present in this kernel[36].The breakup frequency increases with increasing droplet diameter,increasing turbulent energy dissipation rate,increasing density of the continuous phase and decreasing of the interfacial tension.

3.5.MF breakup kernel

In the multifractal(MF)breakup model derived by Bałdyga and Podgórska[31]the pressure fluctuations are considered responsible for droplet breakup.It was assumed that eddies of the size comparable with that of droplet can disperse the drop,but not all of them are active enough.The difference in activity of eddies of the same scale results from internal intermittency.In our previous work,MF breakup kernel was shown to predict accurately the time evolution of the mean Sauter diameter when turbulent intermittency plays an important role[46].The MF breakup kernel is reported as follows:

whereCg=0.0035,Lis the integral turbulent length scale(and is calculated as follows:Lαmin=0.12,whereas the upper bound of the multifractal exponent α for vigorous eddies,αx,is given by the following expression:

whereCx=0.23.It should be noted that when the disperse phase viscosity is high,different αxshould be formulated.More details about the MF breakup kernel can be found in the work by Bałdyga and Podgórska[31].

In all breakup kernels mentioned above,the presence of the surfactant molecules influences the drop size only by the interfacial tension reduction.To a first approximation,the droplet size may be estimated by using the static interfacial tension in the presence of surfactant.However,during droplet stretching surfactant may be removed from the interface.As the new interface is created,the rate at which surfactant diffuses to the surface again may not be sufficient to maintain a constant interfacial tension.For example,for the liquidliquid dispersions containing Tween 20,an additional force resulting from the difference between dynamic and equilibrium interfacial tension may arise[42].The dynamic interfacial tension of this fresh surface(fort→0)σt→0is higher than the static one,σ,and in the case of low surfactant concentration is equal practically to that for systems without surfactant σ0.The extra stress generated due to the difference in interfacial tension Δσ=σ0-σ adds to the turbulent dispersive stress.In order to take into account this extra stress Bąk and Podgórska[42]modified the expression for the multifractal exponent αx,characterizing the weakest eddies that can disperse the drop at the presence of small amounts of surfactant.This modified multifractal exponent αxis given by

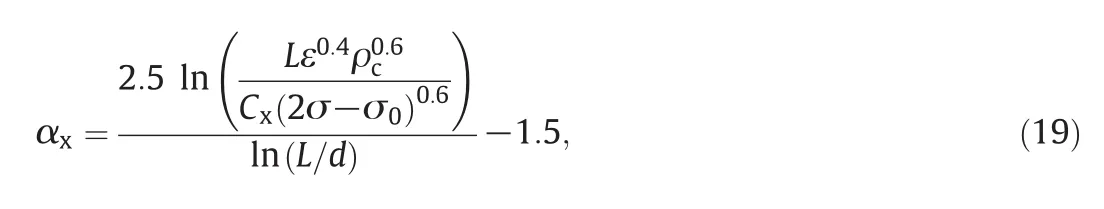
where σ0is the interfacial tension for the system without surfactant.In this study,Eq.(19)is used for the multifractal exponent αxin the MF breakup kernel for test A group,in which Tween 20 is the surfactant employed,whereas Eq.(18)is used for test B group in which the surfactant is PVA 88%.This is justified by the assumption that the influence of additional disruptive stress on drop breakup is expected to be negligible in this latter case due to the fact that PVA 88%molecules are strongly adsorbed and are not easily removed from the droplet surfaces[43].The multifractal spectrumf(α)appearing in Eq.(17)has a universal form and is well approximated by the following expression:

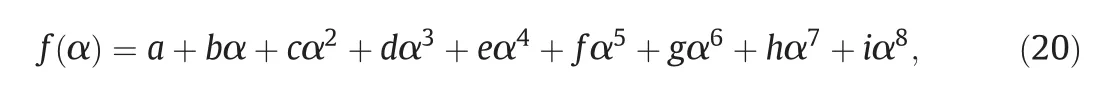
witha=-3.51,b=18.721,c=-55.918,d=120.9,e=-162.54,f=131.51,g=-62.572,h=16.1,i=-1.7264 for α≥0.12.The polynomial coefficients were obtained by fitting to experimental spectrum of Meneveau and Sreenivasan[78].

4.Test Cases and Numerical Details

These two surfactants were added into the toluene-water system(toluene as disperse phase and water as continuous phase).The original experimental data can be found in the work of Bąk and Podgórska[42,43].

The solver compressibleTwoPhaseEulerFoam of OpenFOAM-2.2.x was adopted to predict the liquid-liquid flow fields.In our previous works,QMOM with six moments(and therefore three nodes and three weights of quadrature)and Laakkonen breakup kernelwas implemented to solve PBM to simulate gas-liquid systems[51,52];this solver was then extended by Gaoet al.to simulate liquid-liquid dispersions with different viscosities of the disperse phase to predict the time evolution of the mean Sauter diameter with the CT breakup kernel and the MF breakup kernel[46].Then EQMOM was implemented in this code to simulate coalescence and breakup for liquid-liquid dispersions in stirred tanks[47].In this work,the additional modified MF,Alopaeus,MB and Lehr breakup kernels are implemented to investigate their performance when different surfactants are included.

The experiments were performed in the tank with the geometry sketched in Fig.1.The surfactant,impeller rotational speed,concentration of the surfactant,interfacial tension and the initial mean Sauter diameter for each case are reported in Table 1.The Power number of each test case is 5.5.The computational meshes,discretizing only half of the geometry by means of periodic boundary conditions,were generated with Ansys ICEM and then exported into the OpenFOAM environment.The total number of elements in the symmetric half of the stirred tank was equal to 213067.The impeller blades,disk and baffles were represented as zero-thickness objects.The disperse phase and continuous phase viscosities are 5.5×10-4Pa·s and 8.9×10-4Pa·s,respectively.The density of the disperse phase and the continuous phase is 862.3 kg·m-3and 997 kg·m-3and the global disperse phase volume fraction is 0.05(corresponding to 5%).To reduce the computational costs of the simulation,the motion of the stirrer was modeled by using the Multiple Reference Frame(MRF)approach[79].The numerical solution of the integral in Eq.(17)was carried out with a Gauss-Legendre rule with five(fixed)nodes,which was proven to be a good compromise between computational costs and accuracy[46].

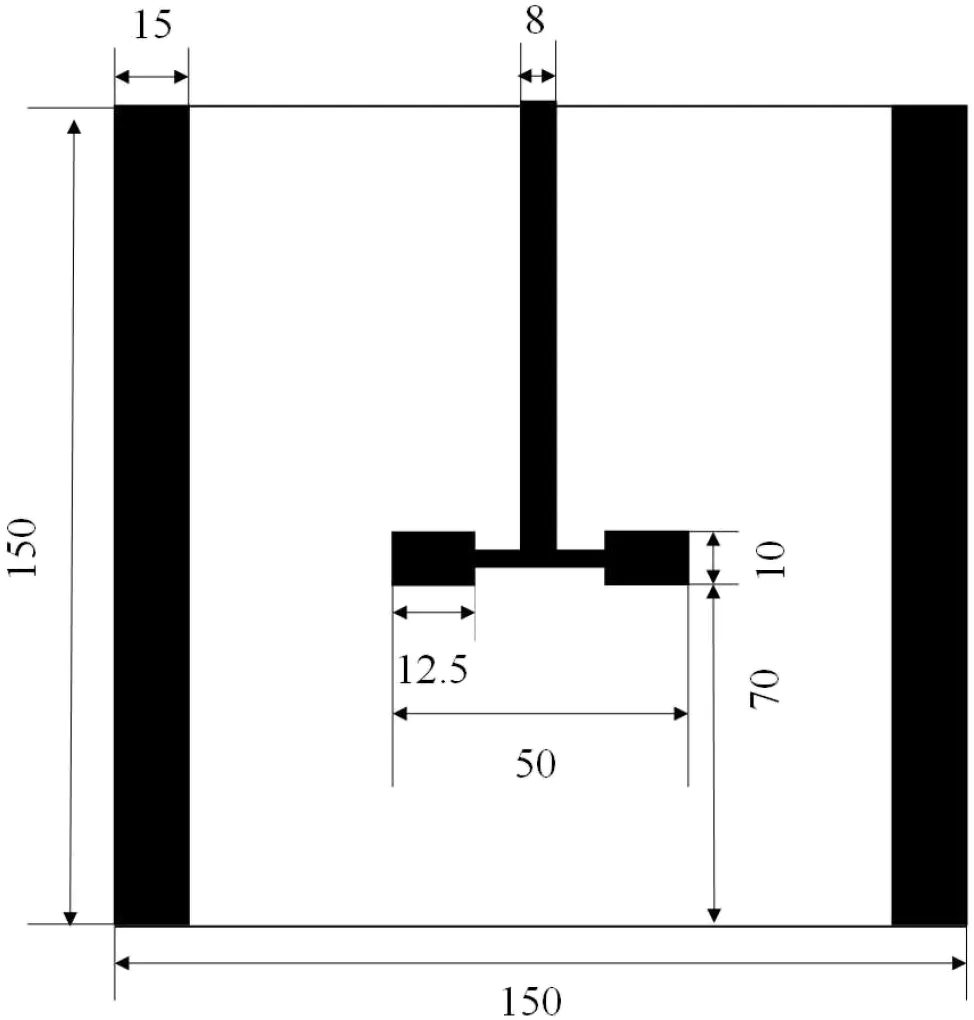
Fig.1.Geometries of the stirred tanks investigated in this work.Quotes are in mm.

The velocity-pressure coupling was solved by the PISO algorithm[80]implemented in OpenFOAM.In our cases,the experiments were carried out in a long period and the disperse phase is quite dilute.Hence,the weak coupling ofCFDand PBMmethod described in ourprevious work[46]is adopted in order to speed up the simulation.When moment transport equations are added to the system of equations to solve,the calculation of the moment source terms is the major timeconsuming step[47].The actual computational time depends on the specific PBM solving method and the specific breakup and coalescence kernels.All the simulations are carried out on a machine with an Intel i7-5820k CPU with 6 cores(12 threads)for parallel computing.On this machine,the time needed for the calculation of the source term in the Eq.(8)with three quadrature nodes varied from around 0.2 s(MB breakup kernel and Alopaeus breakup kernel)to around 1.2 s(MF breakup kernel)depending on the complexity of the breakup kernel.It is worth mentioning that these values are not absolute,since they may depend also on the adopted grid size.

5.Results

5.1.Analysis of breakup frequency

The dependency of the breakup frequency on the droplet diameter,as well as the influence of the turbulent kinetic energy dissipation rate,and interfacial tension for the CT breakup kernel are shown in Fig.2.In this figure,the CT breakup kernel predicts a maximum breakup rate for a certain droplet size.This maximum droplet size varies from0.2 mm to 2 mm,when the interfacial tension is fixed and the turbulent dissipation rate is changed.It does not vary much(below 0.05 mm)when different interfacial tensions are considered and the turbulent kinetic energy dissipation rate is fixed.

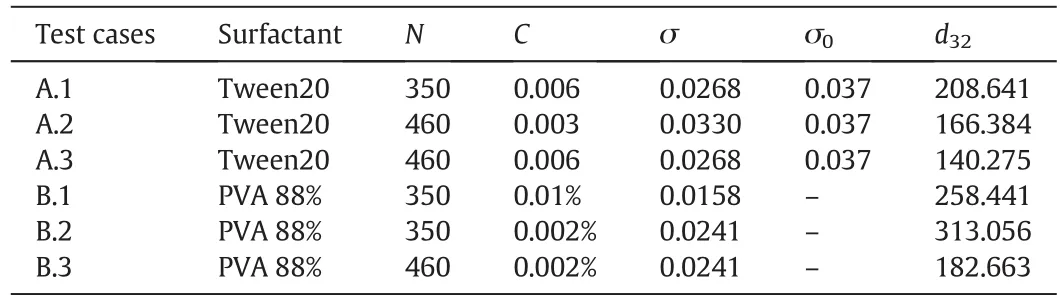
Table 1Surfactant properties and operating conditions investigated in this work:N is the impeller rotational speed(r·min-1),C is the concentration(for Tween 20 in mmol,for PVA 88%in mass percentage),σ and σ0 are the static and dynamic(for t→0)interfacial tension between the two phases(N·m-1),and d32 is the initial mean Sauter diameter(μm)

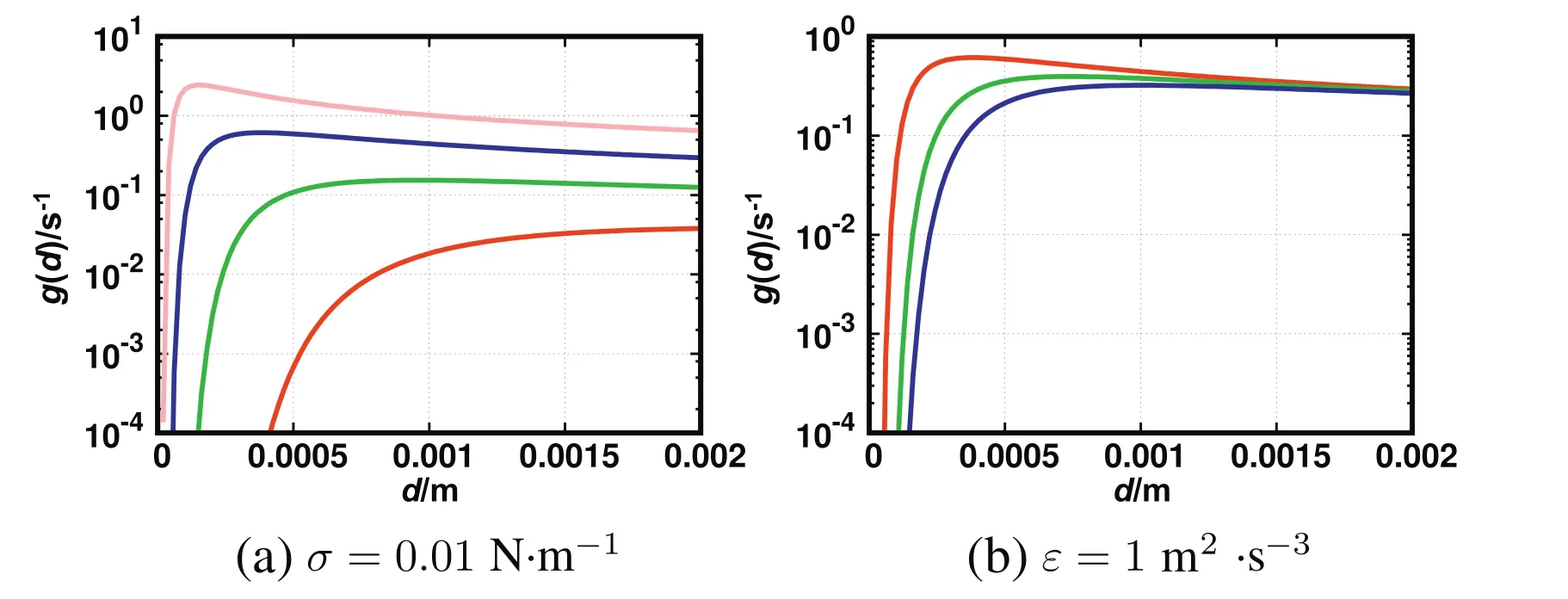
Fig.2.Plot of CT breakup frequency for different turbulent energy dissipation rates with fixed interfacial tension(top,σ=0.01 N·m-1),ε=0.01 m2·s-3(red),ε=0.1 m2·s-3(green),ε=1 m2·s-3(blue),ε=10 m2·s-3(pink),and different interfacial tensions with fixed turbulent energy dissipation rate(bottom,ε=1 m2·s-3),σ=0.01 N·m-1(red),σ=0.03 N·m-1(green),σ=0.05 N·m-1(blue).Note the logarithmic scale for the breakup frequency.

The breakup frequencyversusthe droplet diameter for the MB breakup kernel is shown in Fig.3.In this plot,the diameter range is enlarged to 0.01 m as the MB breakup frequency plot for ε=0.01 m2·s-3starts afterd≥0.008 m.Apeak value exists also for the MB kernel,as also seen for the CT kernel.Butthis peak value differs when the turbulent kinetic energy dissipation rate changes.Meanwhile,whend＜dc,the breakup frequency of the MB breakup kernel is assumed to be zero,and it increases rapidly for droplets larger than the critical one,d＞dc.After reaching a maximum,the breakup frequency decreases monotonically with the droplet size.This kind of shape will cause a problem when the droplet size is smaller thandcbecause it predicts no breakup phenomenon which is incorrect for the liquid-liquid dispersion test cases in this study.This is further verified by our three-dimensional simulations,reported in the next section.When different interfacial tension values are considered,the breakup frequency differs much and it tends to be zero in most cases.

The plotofthe breakup frequencyversusthe droplet diameterfor the Alopaeus breakup kernel is shown in Fig.4.Compared with the CT and MB breakup kernels,the Alopaeus breakup kernel does not predict a maximum breakup frequency.The breakup frequency increases quickly,when the size of the droplet is below the range:0-1000 μm,but then it remains nearly stable.When different interfacial tension values are considered,the breakup frequency differs not much and it keeps increasing with the increasing droplet size.

The plot of the breakup frequencyversusdroplet diameter for the Lehr breakup kernel is shown in Fig.5.As it can be seen,the kernel predicts much higher breakup frequencies(in the order of 106)than the other breakup kernels,for ε=10 m2·s-3.However,although it predicts very high breakup frequencies for high turbulent kinetic energy dissipation rates,for droplet diameters between 200 μm and 300 μm,from medium to low turbulent kinetic energy dissipation rate values,the breakup frequency is very small(in the order of 10-20s-1).This value is much lower than what was predicted by the other breakup kernels.The kernel also predicts that the breakup frequency increases heavily with the increase of droplet size and predictions do not change much when different interfacial tension values are considered.

Fig.3.Plot of MB breakup frequency for different turbulent energy dissipation rates with fixed interfacial tension(top,σ=0.01 N·m-1),ε=0.01 m 2· s-3(red),ε=0.1 m 2· s-3(green),ε=1 m 2· s-3(blue),ε=10 m 2· s-3(pink),and different interfacial tensions with fixed turbulent energy dissipation rate(bottom,ε=1 m 2· s-3),σ=0.01 N·m-1(red),σ=0.03 N·m-1(green),σ=0.05 N·m-1(blue).

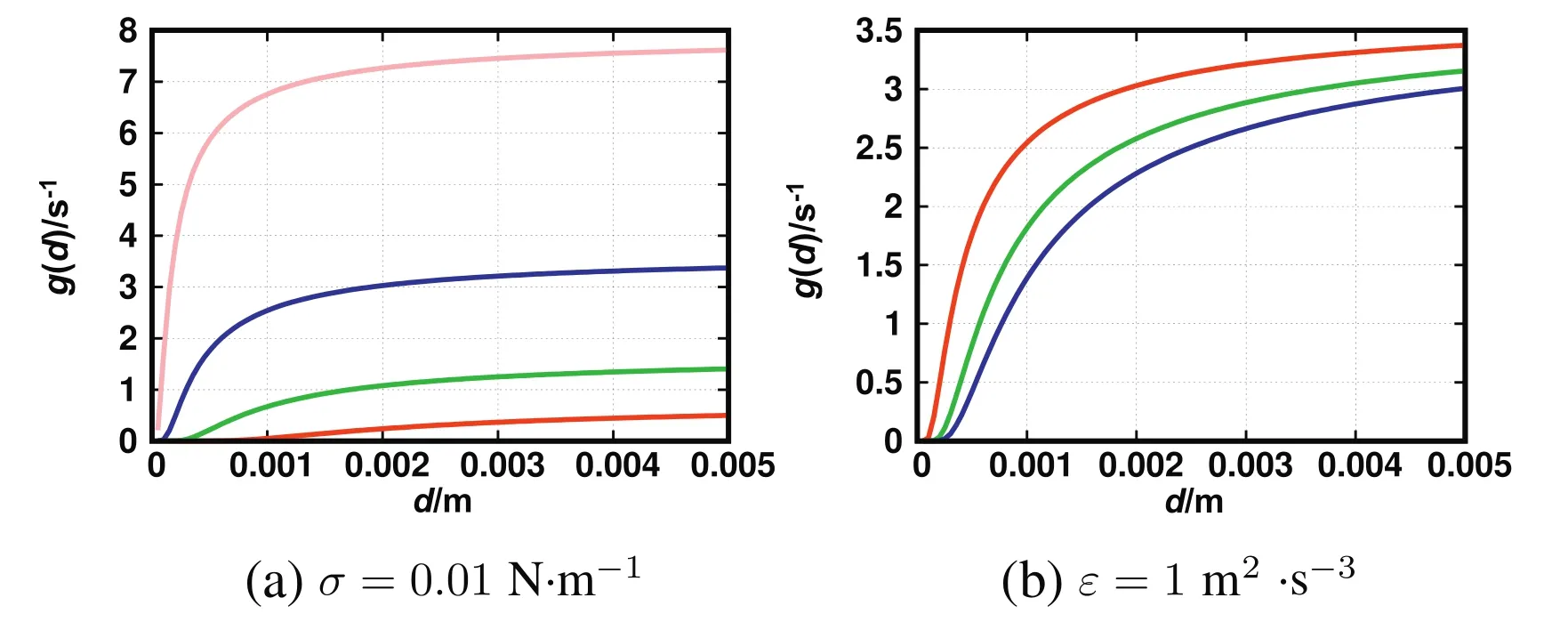
Fig.4.Plot of Alopaeus breakup frequency for different turbulent energy dissipation rate with fixed interfacial tension(top,σ=0.01 N·m-1),ε=0.01 m2·s-3(red),ε=0.1 m2·s-3(green),ε=1 m2·s-3(blue),ε=10 m2·s-3(pink),and different interfacial tensions with fixed turbulent energy dissipation rate(bottom,ε=1 m2·s-3),σ=0.01 N·m-1(red),σ=0.03 N·m-1(green),σ=0.05 N·m-1(blue).

Finally,the breakup frequency is plottedversusthe droplet size for the MF breakup kernel in Fig.6.In contrast to previous breakup kernels,the MF breakup kernel includes the integral length scale of turbulence,L,which depends on the system scale and results from taking into account internal intermittency.In the plot,the integral length scale of turbulence is equal to 0.005 m.Closer observation of Fig.6 reveals that the dependency over droplet size of the MF breakup kernel is similar to that of the CT breakup kernel.However,the decrease of the breakup rate for small droplets,predicted by the MF kernel,is not as steep as what was predicted by the CT kernel.In addition,for the liquid-liquid system in which the surfactant is Tween 20,the extra stress resulting from the interfacial tension difference is included into the MF breakup kernel.As a result of this,the breakup frequency for the dispersion containing Tween 20 predicted by this kernel is higher than that predicted by CT breakup kernel.The influence of additional disruptive stress on the breakup rate is presented in Fig.6,in which predictions of the original and modified MF kernels are compared.

5.2.Simulated flow field and breakup frequency

The contour plots of the turbulent kinetic energy dissipation rate,the turbulent kinetic energy and the mean Sauter diameter for the test Case B.1 with CT breakage kernel are reported in Fig.7.Most of the turbulent kinetic energy is dissipated near the impeller,where the breakup frequency is expected to be very high.Meanwhile,as the system is dilute,the disperse phase is distributed rather homogeneously and the mean Sauter diameter is uniform in the vessel,which is consistent with our previous work[46].

It is also interesting to compare the breakup frequency predicted by the different kernels in our three-dimensional simulations:they are reported in Fig.8.It can be seen that the breakup frequency is rather high in the vicinity of the blades for the CT,MFand Alopaeus breakup kernels.Similar behaviors are also reported in the literature[81].In this region,the droplet undergoes a strong shear and breakup.It is worth observing that the breakup frequency predicted by the CT kernel is larger than the MF and Alopaeus breakup kernels.The breakup frequency for the MB and Lehr breakup kernels is severely underestimated.This is consistent with the results reported in Fig.3 and in Fig.5.Even for the highest turbulent kinetic energy dissipation rate(i.e.in the vicinity of impeller)the breakup frequency predicted for test Case B.1 by the MB and Lehr breakup kernels is practically equal to zero.

5.3.Comparison with experiments

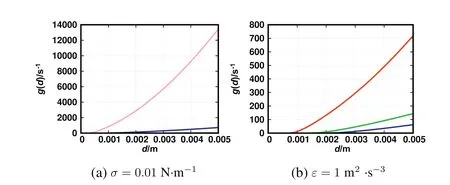
Fig.5.Plot of Lehr breakup frequency for different turbulent energy dissipation rates with fixed interfacial tension(top,σ=0.01 N·m-1),ε=0.01 m2·s-3(red),ε=0.1 m2·s-3(green),ε=1 m2·s-3(blue),ε=10 m2·s-3(pink),and different interfacial tensions with fixed turbulent energy dissipation rate(bottom,ε=1 m2·s-3),σ=0.01 N·m-1(red),σ=0.03 N·m-1(green),σ=0.05 N·m-1(blue).

Fig.6.Plot of MF breakup frequency for different turbulent energy dissipation rates with fixed interfacial tension(top,σ=0.01 N·m-1),ε=0.01 m2·s-3(red),ε=0.1 m2·s-3(green),ε=1 m2·s-3(blue),ε=10 m2·s-3(pink),and different interfacial tensions with fixed turbulent energy dissipation rate(middle,ε=1 m2·s-3),σ=0.01 N·m-1(red),σ=0.03 N·m-1(green),σ=0.05 N·m-1(blue),and fixed interfacial tension and fixed turbulent energy dissipation rate(bottom,σ=0.0268 N·m-1,ε=1 m2·s-3)with(green)or without(red)additional disruptive stress resulting from the interfacial tension difference(σ-σ0),where σ0=0.037 N·m-1.Note the logarithmic scale for the breakup frequency.

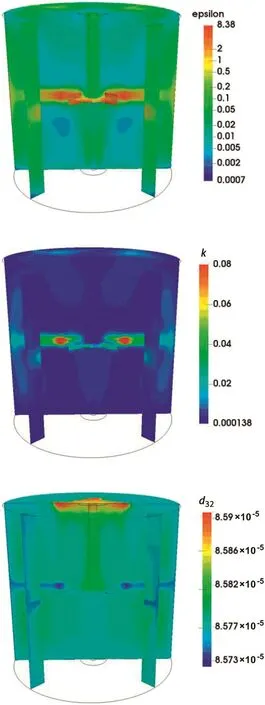
Fig.7.Contour plots of the turbulentkinetic energy dissipation rate(ε,m2·s-3),turbulent kinetic energy(k,m2·s-2)and mean Sauter diameter(d,m)for Case B.1 with CT breakage kernel.

The comparison of the time evolution of the mean Sauter diameter predicted by these breakup kernels with experimental data for Case B.1 is reported in Fig.9.As can be seen the Lehr and MB breakup kernels do not result in reasonable predictions as no noticeable breakup takes place.The Lehrbreakup kernel was developed originally to predict bubble size distributions in bubble columns,with high super ficial gas velocity[36],and with bubbles in the size range of 1000 μm to 5000 μm.However,in our test cases,the average value of the mean Sauter diameter of the droplets is around 200 μm,which is far smaller than the bubble size in the original work.As there is no fitting parameter,we can come to the conclusion that the Lehr breakup kernel is not a good choice to simulate our liquid-liquid dispersions,in which the value of mean Sauter diameter is very small.Similarly,the MB breakup kernel is developed originally to predict the breakup frequency for air bubbles injected with very high velocity(e.g.,17 m·s-1)into a fully developed turbulent water jet[32].In their test cases,the turbulent kinetic energy dissipation rate ranges from 0 to 3000 m2·s-3,which is much higher than the values characterizing our test cases(e.g.,〈ε〉≈0.15 m2·s-3).Even though the single fitting parameter could be used to improve agreement,this cannot be done in this case as the breakup frequency is zero whend＜dc.Hence,in the following test cases,the results of the MB and the Lehr breakup kernels are not reported.

The comparison of the time evolution of the mean Sauter diameter with experimental data for Cases B.2 and B.3 is reported in Fig.10.As can be seen the time evolution of the mean Sauter diameter predicted by MF breakup kernel for these test cases agrees well with the experimental data.Similarly with Case B.1,the final value of the mean Sauterdiameter atsteady-state predicted by the CT and Alopaeus breakup kernels is slightly lower than the MF breakup kernel.

Let us now discuss the time evolution of the mean Sauter diameter for the Case A group.The comparison of the time evolution of the mean Sauter diameter with experimental data for Cases A.1,A.2 and A.3 is reported in Fig.11.In this group,the surfactant is Tween 20.As discussed above,this surfactant can desorb from the drop surface during its deformation giving rise to additional stresses,due to the interfacial tension difference,which increases the drop breakup frequency.This effect was taken into account in the modified MF breakup model.As seen the MF kernel again properly predicts the time evolution of the droplet size.The CT and Alopaeus kernels,which previously(when surfactant was not removed from the surface as in case group B)predicted too small droplets,now result in predictions that agree well with experimental data.

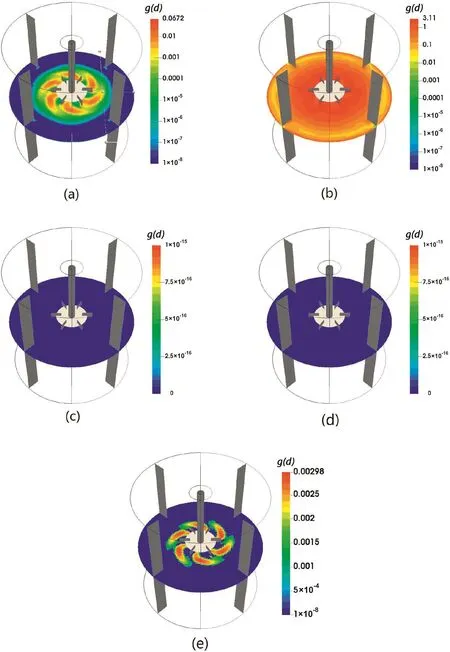
Fig.8.Contour plots of breakup frequency(g(d),s-1),for CT(left on the top,d=60.10 μm),MF(middle on the top,d=85.76 μm),MB(right on the top,d=258.4 μm),Alopaeus(left on the bottom,d=69.97 μm)and Lehr(right on the bottom,d=258.4 μm)breakup kernel for Case B.1( final drop sizes are given).

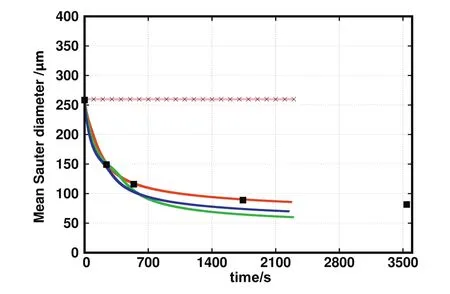
Fig.9.Comparison for the time evolution of the mean Sauter diameter predicted by CT(green),MF(red),Alopaeus(blue),MB(pink)and Lehr(light blue)kernels with experimental data(symbols)for Case B.1.

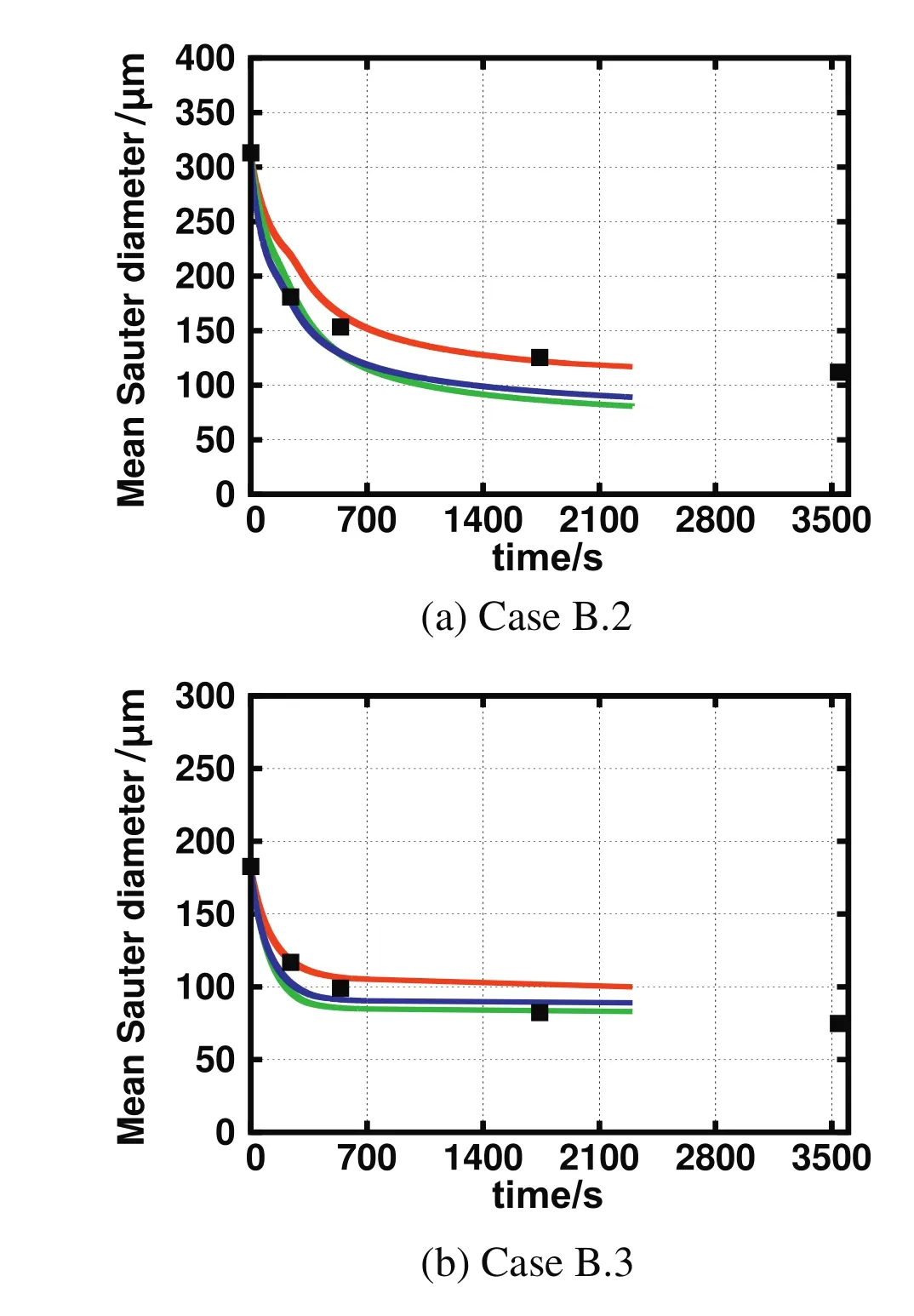
Fig.10.Comparison for the time evolution of the mean Sauter diameter predicted by CT(green),MF(red),and Alopaeus(blue)kernels with experimental data(symbols)for Case B.2(top)and Case B.3(bottom).

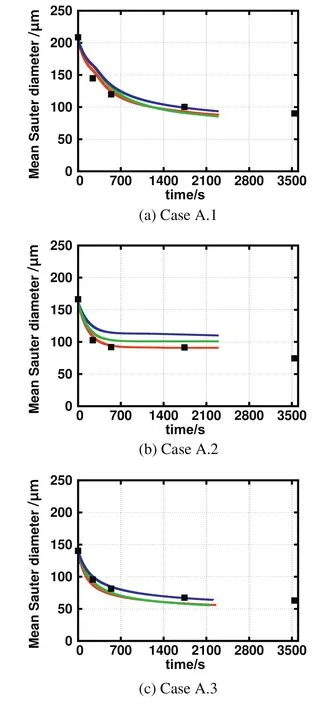
Fig.11.Comparison for the time evolution of the mean Sauter diameter predicted by CT(green),MF(red),and Alopaeus(blue)kernels with experimental data(symbols)for Cases A.1(top),A.2(middle)and A.3(bottom).

6.Conclusions

In this work,the PBM,solved with QMOM,is coupled with the TFM to simulate turbulent liquid-liquid dispersions with different surfactants in stirred tanks.Five different breakup models(the CT,Alopaeus,MB,Lehr and the MF kernels)were tested in our simulations and coupled with the open-source CFD code OpenFOAM.Six different test cases were simulated in a stirred tank equipped with a Rushton impeller,working under different stirring rates,and with different compositions resulting in different interfacial tension values.Eventually the time evolution of the mean Sauter diameter predicted by these breakup kernels is compared with experimental data,providing our simulations with the necessary validation.

Our results show that the adequate parameter for the MB breakup kernel cannot be found for our liquid-liquid dispersions.The Lehr breakup kernel(which does not contain any adjustable parameter)does not predict breakup of droplets,so they stay unchanged while undergoing mixing in the tank.Hence,the Lehr and the MB breakup kernels,which were originally developed for gas bubbles,do not seem to be suitable for our liquid-liquid dispersions.For the liquid-liquid dispersions with PVA 88%as surfactant,the MF breakup kernel can predict an accurate time evolution of the mean Sauter diameter.The CT and Alopaeus kernels slightly underestimate the mean Sauter diameter,meaning that the predicted breakup frequency is too high.For the liquid-liquid dispersions with Tween 20 as surfactant,when additional stresses are generated,the MF breakup kernel predicts again accurate results.It should be underlined here,that taking these additional stresses into account does not introduce any new parameter into the kernel and that all the simulations are performed with the original model parameters.Interestingly enough the results predicted by the CT and Alopaeus breakup kernels are now also satisfying.This can be due to the fact that they generally predict too fast breakup and in the situation when there exists additional disruptive stresses,that are not taken into account,their predictions coincide with experiments.

Nomenclature

CDdrag coefficient

Cgconstant for MF breakup kernel

Ck1k-ε model parameters

Ck2k-ε model parameters

Cxconstant for MF breakup kernel

Cμk-ε model parameters

C1constant for breakup kernel

C2constant for breakup kernel

C3constant for breakup kernel

ddroplet size,m

dccritical droplet size,m

d′ mother droplet size,m

dαabscissas of the quadrature approximation,m-3

d32mean Sauter diameter,m

Gkproduction of the turbulent kinetic energy

g gravitational acceleration vector,N·m-2

kturbulent kinetic energy,m2·s-2

Lintegral turbulent length scale,m

Mdinterfacial force,N

mkkth moment of number density function,mk-3

Nimpeller rotational speed,r·min-1

paverage pressure,Pa

RdReynolds-stress tensor,N·m-2

ttime,s

Ucvelocity of continuous phase,m·s-1

Udvelocity of disperse phase,m·s-1

Urslip velocity,m·s-1

wαweights of the quadrature approximation,m-3

α multifractal exponent

αcvolume fraction of continuous phase

αdvolume fraction of disperse phase

αmininfimum of multifractal exponent

αxupper bound of multifractal exponent for vigorous eddies

ε turbulent energy dissipation rate,m2·s-3

μcviscosity of continuous phase,Pa·s

μdviscosity of disperse phase,Pa·s

νtturbulent viscosity,Pa·s

ρcdensity of continuous phase,kg·m-3

ρddensity of disperse phase,kg·m-3

σ static interfacial tension,N·m-1

σkturbulent Schmidt number fork

σεturbulent Schmidt number for ε

σ0dynamic interfacial tension,N·m-1

τdviscous stress tensor,N·m-2

[1]W.Yan,J.Li,Z.Luo,A CFD-PBM coupled model with polymerization kinetics for multizone circulating polymerization reactors,Powder Technol.231(2012)77-87.

[2]W.Yan,Z.Luo,Y.Lu,X.Chen,A CFD-PBM-PMLM integrated model for the gas-solid flow fields in fluidized bed polymerization reactors,AICHE J.58(2012)1717-1732.

[3]N.Qi,K.Zhang,G.Xu,Y.Yang,H.Zhang,CFD-PBE simulation of gas-phase hydrodynamics in a gas-liquid-solid combined loop reactor,Pet.Sci.10(2013)251-261.

[4]E.Abbasi,J.Abbasian,H.Arastoopour,CFD-PBE numerical simulation of CO2capture using MgO-based sorbent,Powder Technol.286(2015)616-628.

[5]S.Kumar,D.Ramkrishna,On the solution of population balance equations by discretization—I.A fixed pivot technique,Chem.Eng.Sci.51(1996)1311-1332.

[6]Y.Lin,K.Lee,T.Matsoukas,Solution of the population balance equation using constant-number Monte Carlo,Chem.Eng.Sci.57(2002)2241-2252.

[7]A.Buffo,M.Vanni,D.Marchisio,R.Fox,Multivariate quadrature-based moments methods for turbulent polydisperse gas-liquid systems,Int.J.Multiphase Flow50(2013)41-57.

[8]W.Zhang,C.You,Numerical approach to predict particle breakage in dense flows by coupling multiphase particle-in-cell and Monte Carlo methods,Powder Technol.283(2015)128-136.

[9]M.Hussain,J.Kumar,E.Tsotsas,Modeling aggregation kinetics of fluidized bed spray agglomeration for porous particles,Powder Technol.270(2015)584-591.

[10]R.McGraw,Description of aerosol dynamics by the quadrature method of moments,Aerosol Sci.Technol.27(1997)255-265.

[11]D.Marchisio,R.Fox,Solution of population balance equations using the direct quadrature method of moments,J.Aerosol Sci.36(2005)43-73.

[12]J.Su,Z.Gu,Y.Li,S.Feng,X.Xu,An adaptive direct quadrature method of moment for population balance equations,AICHE J.54(2008)2872-2887.

[13]M.Yu,J.Lin,T.Chan,A new moment method for solving the coagulation equation for particles in Brownian motion,Aerosol Sci.Technol.42(2008)705-713.

[14]C.Yuan,F.Laurent,R.Fox,An extended quadrature method of moments for population balance equations,J.Aerosol Sci.51(2012)1-23.

[15]J.Cheng,C.Yang,Z.Mao,C.Zhao,CFD modeling of nucleation,growth,aggregation,and breakage in continuous precipitation of barium sulfate in a stirred tank,Ind.Eng.Chem.Res.48(2009)6992-7003.

[16]P.Lage,On the representation of QMOM as a weighted-residual method—the dualquadrature method of generalized moments,Comput.Chem.Eng.35(2011)2186-2203.

[17]J.Cheng,C.Yang,Z.Mao,CFD-PBE simulation of premixed continuous precipitation incorporating nucleation,growth and aggregation in a stirred tank with multi-class method,Chem.Eng.Sci.68(2012)469-480.

[18]J.Pedel,J.Thornock,P.Smith,Large eddy simulation of pulverized coal jet flame ignition using the direct quadrature method of moments,Energy Fuel26(2012)6686-6694.

[19]R.Upadhyay,Evaluation of the use of the Chebyshev algorithm with the quadrature method of moments for simulating aerosol dynamics,J.AerosolSci.44(2012)11-23.

[20]C.Frances,A.Liné,Comminution process modeling based on the monovariate and bivariate direct quadrature method of moments,AICHE J.60(2014)1621-1631.

[21]Y.Yao,J.Su,Z.Luo,CFD-PBM modeling polydisperse polymerization FBRs with simultaneous particle growth and aggregation:the effect of the method of moments,Powder Technol.272(2015)142-152.

[22]M.Attarakih,M.Hlawitschka,M.Abu-Khader,S.Al-Zyod,H.Bart,CFD-population balance modeling and simulation of coupled hydrodynamics and mass transfer in liquid extraction columns,Appl.Math.Model.39(2015)5105-5120.

[23]M.Yu,Y.Liu,J.Lin,M.Seipenbusch,Generalized TEMOM scheme for solving the population balance equation,Aerosol Sci.Technol.49(2015)1021-1036.

[24]X.Liang,H.Pan,Y.Su,Z.Luo,CFD-PBM approach with modified drag model for the gas-liquid flow in a bubble column,Chem.Eng.Res.Des.112(2016)88-102.

[25]H.Pan,X.Chen,X.Liang,L.Zhu,Z.Luo,CFD simulations of gas-liquid-solid flow in fluidized bed reactors—a review,Powder Technol.299(2016)235-258.

[26]C.Coulaloglou,L.Tavlarides,Description of interaction processes in agitated liquidliquid dispersions,Chem.Eng.Sci.32(1977)1289-1297.

[27]M.Konno,M.Aoki,S.Saito,Scale effect on breakup process in liquid-liquid agitated tanks,J.Chem.Eng.Jpn16(1983)312-319.

[28]H.Luo,H.Svendsen,Theoretical model for drop and bubble breakup in turbulent dispersions,AICHE J.42(1996)1225-1233.

[29]T.Wang,J.Wang,Y.Jin,A novel theoretical breakup kernel function for bubbles/droplets in a turbulent flow,Chem.Eng.Sci.58(2003)4629-4637.

[30]J.Bałdyga,J.Bourne,Interpretation of turbulent mixing using fractals and multifractals,Chem.Eng.Sci.50(1995)381-400.

[31]J.Bałdyga,W.Podgórska,Drop break-up in intermittent turbulence:maximum stable and transient sizes of drops,Can.J.Chem.Eng.76(1998)456-470.

[32]C.Martínez-Bazán,J.Montañés,J.Lasheras,On the breakup of an air bubble injected into a fully developed turbulent flow.Part 1.Breakup frequency,J.Fluid Mech.401(1999)157-182.

[33]J.C.Lasheras,C.Eastwooda,C.Martínez-Bazán,J.Montañés,A review of statistical models for the break-up of an immiscible fluid immersed into a fully developed turbulent flow,Int.J.Multiphase Flow28(2002)247-278.

[34]F.Lehr,D.Mewes,A transport equation for the interfacial area density in two-phase flow,Second European Congress ofChemicalEngineering,Montpellier,France,1999.

[35]F.Lehr,D.Mewes,A transport equation for the interfacial area density applied to bubble columns,Chem.Eng.Sci.56(2001)1159-1166.

[36]F.Lehr,M.Millies,D.Mewes,Bubble-size distributions and flow fields in bubble columns,AICHE J.48(2002)2426-2443.

[37]T.Wang,J.Wang,J.Jin,An efficient numerical algorithm for a novel theoretical breakup kernel function of bubble/droplet in a turbulent flow,Chem.Eng.Sci.59(2004)2593-2595.

[38]F.Ghasempour,R.Andersson,B.Andersson,D.Bergstrom,Number density of turbulent vortices in the entire energy spectrum,AICHE J.60(11)(2014)3989-3995.

[39]L.Han,S.Gong,Y.Li,Q.Ai,H.Luo,Z.Liu,Y.Liu,A novel theoretical model of breakage rate and daughter size distribution for droplet in turbulent flows,Chem.Eng.Sci.102(2013)186-199.

[40]L.Han,S.Gong,Y.Li,N.Gao,J.Fu,Z.Liu,et al.,Influence of energy spectrum distribution on drop breakage in turbulent flows,Chem.Eng.Sci.117(2014)55-70.

[41]J.Solsvik,H.Jakobsen,Development of fluid particle breakup and coalescence closure models for the complete energy spectrum of isotropic turbulence,Ind.Eng.Chem.Res.55(2016)1449-1460.

[42]A.Bąk,W.Podgórska,Investigation of drop breakage and coalescence in the liquidliquid system with nonionic surfactants Tween 20 and Tween 80,Chem.Eng.Sci.74(2012)181-191.

[43]A.Bąk,W.Podgórska,Drop breakage and coalescence in the toluene/water dispersions with dissolved surface active polymers PVA 88%and 98%,Chem.Eng.Res.Des.91(2013)2142-2155.

[44]A.Koshy,T.Das,R.Kumar,Effect of surfactants on drop breakage in turbulent liquid dispersions,Chem.Eng.Sci.43(1988)649-654.

[45]V.Alopaeus,J.Koskinen,K.Keskinen,J.Majander,Simulation of the population balances for liquid-liquid systems in a nonideal stirred tank.Part 2—parameter fitting and the use of the multiblock model for dense dispersions,Chem.Eng.Sci.57(2002)1815-1825.

[46]Z.Gao,D.Li,A.Buffo,W.Podgórska,D.Marchisio,Simulation of droplet breakage in turbulent liquid-liquid dispersions with CFDPBM:comparison of breakage kernels,Chem.Eng.Sci.142(2016)277-288.

[47]D.Li,A.Buffo,W.Podgórska,Z.Gao,D.Marchisio,Droplet breakage and coalescence in liquid-liquid dispersions:comparison of different kernels with EQMOM and QMOM,AIChE J.63(2017)2293-2311.

[48]W.Podgórska,D.Marchisio,Modeling of turbulent drop coalescence in the presence of electrostatic forces,Chem.Eng.Res.Des.108(2016)30-41.

[49]A.Buffo,J.De Bona,M.Vanni,D.Marchisio,Simplified volume-averaged models for liquid-liquid dispersions:correct derivation and comparison with other approaches,Chem.Eng.Sci.153(2016)382-393.

[50]J.De Bona,A.Buffo,M.Vanni,D.Marchisio,Limitations of simple mass transfer models in polydisperse liquid-liquid dispersions,Chem.Eng.J.296(2016)112-121.

[51]A.Buffo,D.Marchisio,M.Vanni,P.Renze,Simulation of polydisperse multiphase systems using population balances and example application to bubbly flows,Chem.Eng.Res.Des.91(2013)1859-1875.

[52]A.Buffo,D.Marchisio,M.Vanni,On the implementation of moment transport equations in OpenFOAM to preserve conservation,boundedeness and realizability,International Conference on Multiphase Flows in Industrial Plants,Sestri Levante,September 16-19,2014.

[53]D.Drew,Mathematical modeling of two-phase flow,Annu.Rev.Fluid Mech.15(1982)261-291.

[54]D.Drew,S.Passman,Theory of Multicomponent Fluids,vol.135,Springer,2006.

[55]A.Gosman,C.Lekakou,S.Politis,R.Issa,M.Looney,Multidimensional modeling of turbulent two-phase flows in stirred vessels,AICHE J.38(1992)1946-1956.

[56]L.Schiller,A.Naumann,A drag coefficient correlation,VDI Zeitung77(1935)51-86.

[57]A.Behzadi,R.Issa,H.Rusche,Modelling of dispersed bubble and droplet flow athigh phase fractions,Chem.Eng.Sci.59(2004)759-770.

[58]M.Petitti,A.Nasuti,D.Marchisio,M.Vanni,G.Baldi,N.Mancini,F.Podenzani,Bubble size distribution modeling in stirred gas-liquid reactors with QMOM augmented by a new correction algorithm,AICHE J.56(2010)36-53.

[59]G.Montante,K.Lee,A.Brucato,M.Yianneskis,Numerical simulations of the dependency of flow pattern on impeller clearance in stirred vessels,Chem.Eng.Sci.56(2001)3751-3770.

[60]E.Paul,V.Atiemo-Obeng,S.Kresta,Handbook of Industrial Mixing:Science and Practice,John Wiley&Sons,2004.

[61]J.Aubin,D.Fletcher,C.Xuereb,Modeling turbulent flow in stirred tanks with CFD:the influence of the modeling approach,turbulence model and numerical scheme,Exp.Thermal Fluid Sci.28(2004)431-445.

[62]C.Wang,R.Calabrese,Drop breakup in turbulent stirred-tank contactors.Part II:relative influence of viscosity and interfacial tension,AICHE J.32(1986)667-676.

[63]A.Gäbler,M.Wegener,A.Paschedag,M.Kraume,The effect of pH on experimental and simulation results of transient drop size distributions in stirred liquid-liquid dispersions,Chem.Eng.Sci.61(2006)3018-3024.

[64]S.Maaß,N.Paul,M.Kraume,Influence of the dispersed phase fraction on experimental and predicted drop size distributions in breakage dominated stirred systems,Chem.Eng.Sci.76(2012)140-153.

[65]D.Ramkrishna,Population Balances:Theory and Applications to Particulate Systems in Engineering,Academic Press,2000.

[66]D.Marchisio,R.Vigil,R.Fox,Quadrature method of moments for aggregationbreakage processes,J.Colloid Interface Sci.258(2003)322-334.

[67]D.Marchisio,R.Fox,Computational Models for Polydisperse Particulate and Multiphase Systems,Cambridge University Press,2013.

[68]C.Martínez-Bazán,J.Montañés,J.Lasheras,On the breakup of an air bubble injected into a fully developed turbulent flow.Part 2.Size PDF of the resulting daughter bubbles,J.Fluid Mech.401(1999)183-207.

[69]C.Tsouris,L.Tavlarides,Breakage and coalescence models for drops in turbulent dispersions,AICHE J.40(1994)395-406.

[70]Y.Liao,D.Lucas,A literature review of theoretical models for drop and bubble breakup in turbulent dispersions,Chem.Eng.Sci.64(2009)3389-3406.

[71]M.Laakkonen,V.Alopaeus,J.Aittamaa,Validation of bubble breakage,coalescence and mass transfer models for gas-liquid dispersion in agitated vessel,Chem.Eng.Sci.61(2006)218-228.

[72]R.Andersson,B.Andersson,On the breakup of fluid particles in turbulent flows,AICHE J.52(2006)2020-2030.

[73]S.Maaß,F.Metz,T.Rehm,M.Kraume,Prediction of drop sizes for liquid-liquid systems in stirred slim reactors—part I:single stage impellers,Chem.Eng.J.162(2010)792-801.

[74]G.Narsimhan,J.Gupta,D.Ramkrishna,A model for transitional breakage probability of droplets in agitated lean liquid-liquid dispersions,Chem.Eng.Sci.34(1979)257-265.

[75]K.Singh,S.Mahajani,K.Shenoy,S.Ghosh,Population balance modeling of liquidliquid dispersions in homogeneous continuous- flow stirred tank,Ind.Eng.Chem.Res.48(2009)8121-8133.

[76]S.Maaß,M.Kraume,Determination of breakage rates using single drop experiments,Chem.Eng.Sci.70(2012)146-164.

[77]G.Batchelor,The Theory of Homogeneous Turbulence,Cambridge University Press,1953.

[78]C.Meneveau,K.Sreenivasan,The multifractal nature of turbulent energy dissipation,J.Fluid Mech.224(1991)429-484.

[79]J.Luo,R.Issa,A.Gosman,Prediction of impeller-induced flow in mixing vessels using multiple frames of reference,8th European Conference on Mixing,Cambridge,1994.

[80]R.Issa,A.Gosman,A.Watkins,The computation of compressible and incompressible recirculating flows by a non-iterative implicit scheme,J.Comput.Phys.62(1986)66-82.

[81]M.Vonka,M.Soos,Characterization of liquid-liquid dispersions with variable viscosity by coupled computational fluid dynamics and population balances,AICHE J.61(2015)2403-2414.