不同加劲板布置下T型方钢管节点内力分析

牛宇辰（同济大学建筑工程系，上海200092）

不同加劲板布置下T型方钢管节点内力分析

牛宇辰
（同济大学建筑工程系，上海200092）

该文基于ABAQUS有限元软件对T型方管节点的无加劲肋板、纵向加劲肋板、横向加劲肋板三种节点形式的弹性模型下力学行为进行数值分析，结果表明横向加劲肋板可以使节点应力集中现象得到有效缓解。此外该文采用理想弹塑性模型对节点进行比较，发现与弹性分析结果相差较大。与规范设计承载力相比，弹塑性模型通过位移控制得到的极限承载力存在一定的冗余。

T型方管节点；加劲板；弹塑性模型；应力集中

0 引言

近年来，T型方钢管节点凭借着形式简单、施工方便等优势得到广泛应用[1-2]。与此同时，为缓解节点处的应力集中现象，实际工程中通常采取加劲措施[3]。实际上，加劲板的布置形式对节点的内力分布有着重要影响[4]。本文通过对某工程中T型方钢管节点在不同加劲板布置形式下分别进行内力分析，为节点设计提供参考依据。

1 建模说明

T型方管节点参数：主管截面为300mm×10mm，长度2000mm，两端铰接。支管截面180mm×8mm，长度为700mm，端部作用均匀轴拉力。支管与主管连接处，截面采用四边角焊缝，有限元分析可视为与主管完全连接，即为不布置加劲板的构造（a）。另两种构造采用一块加劲钢板连接，加劲板截面为290mm×10mm，高度为180mm。分别采用加劲板纵向布置（b）、加劲板横向布置（c）两种方式连接。加劲板与主管、支管相接处均采用双面角焊缝连接，可视为与相连管的板件完全连接，支管端部轴拉力为900kN。采用弹性分析，计算上述3种连接构造下的管内应力。

利用ABAQUS通用有限元软件建立节点模型（图1），单元类型采用三维实体单元，材料采用Q345钢材，弹性模量210000MPa，泊松比0.3，二阶弹塑性分析时采用理想弹塑性模型；非线性分析采用N-R法，初始迭代步长0.01，迭代步数200；网格划分非加密区划分尺寸20，加密区（主管与支管相交处）划分尺寸8。

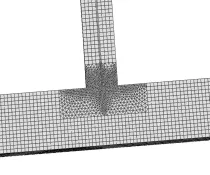
图1 节点模型

2 三种构造节点的弹性分析

2.1 有限元模型分析

分别对三种构造节点进行理想弹性分析，建立相关几何模型和有限元模型，进行几何非线性分析，计算结果如图2所示。

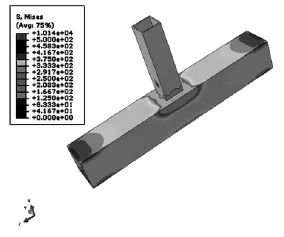
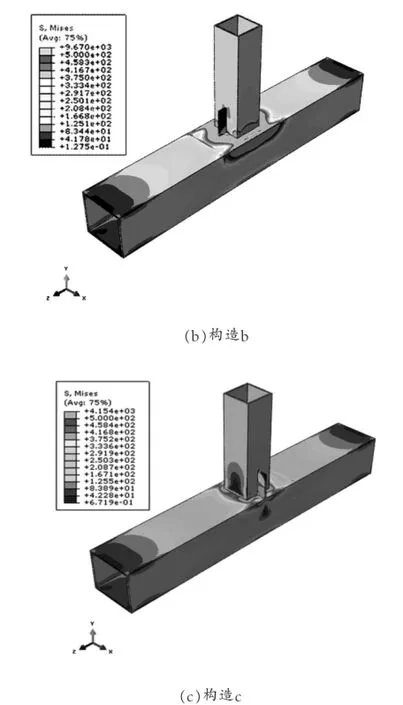
图2 弹性分析节点应力云图

计算可知，节点构造对局部应力分布存在较大影响。

（1）构造（a）在单向拉伸轴力作用下，支管与主管相连部位平行于主管方向的两道焊缝存在较大的应力集中现象，特别在角点处的集中尤为明显，最大应力可达10140MPa。

（2）通过加劲肋板构造可使应力集中现象得到有效缓解，构造（b）在单向拉伸作用下，应力集中得到一定缓解，应力云图有扩散效应，最大应力达到9670MPa，相对无加劲肋板构造最大应力降低4.6%，但由于加劲肋板方向与应力集中区相平行，对应力集中的缓解作用有限，因此降低幅度不明显，在实际设计中应注重加劲肋板方向，提高其效果。

（3）构造（c）在单向拉伸作用下，应力集中区域有较大变化，加劲肋板方向垂直于原应力集中区，使应力集中范围有了明显扩散，最大应力值大幅下降至4154MPa，相对无加劲肋板构造降低59.0%，可见加劲肋板效果相当显著，其有效地将应力集中区域扩散开来，降低了此节点的应力集中系数，通过加劲肋板构造使节点最大应力值下降达到良好效果。

2.2 理论验算

为验证有限元模型建模、分析的合理性，进行简单的理论验算，采用线弹性计算分析，可将整个节点模型简化为：支管为轴心受拉构件，主管为简支梁构件。

计算其杆件受力情况，可知当支管受900kN的轴心拉力时，主管中点受弯最大，为450kN·m，分别计算其最大应力：

支管最大应力：

由上式分析可知，支管轴心受拉，应力相对平均，最大应力163.5MPa，主管受弯，其最大受力位于中点处，分析其边缘受力，最大应力438.1MPa，与应力云图相比较，不考虑其应力集中区域，则支管应力值与计算相吻合，同时应力分布较为均一，主管应力值在下边缘与计算相吻合，上边缘由于应力集中暂不比较，应力分布亦较为合理，与钢管理论分析中塑性铰线理论相吻合，故认为有限元模型、计算均为合理。

3 节点弹塑性分析

基于弹性材料的分析结果，模型最大应力值可以无限增长，往往会超越钢材的屈服强度值，如采用不同构造节点（a）（b）（c），最大应力值分别为10140MPa、9670MPa、4154MPa，超过Q345钢材的屈服强度29.4、28.0、12.0倍，明显与实际情况不符。因此，在材料模型中应使用弹塑性模型，该例为简化计算应用理想弹塑性模型分析比较，即设钢材为理想弹塑性体，屈服点为345MPa，比较不布置加劲板的构造（a）以及加劲板横向布置的构造（c）这两种节点形式的计算结果，如图3所示。

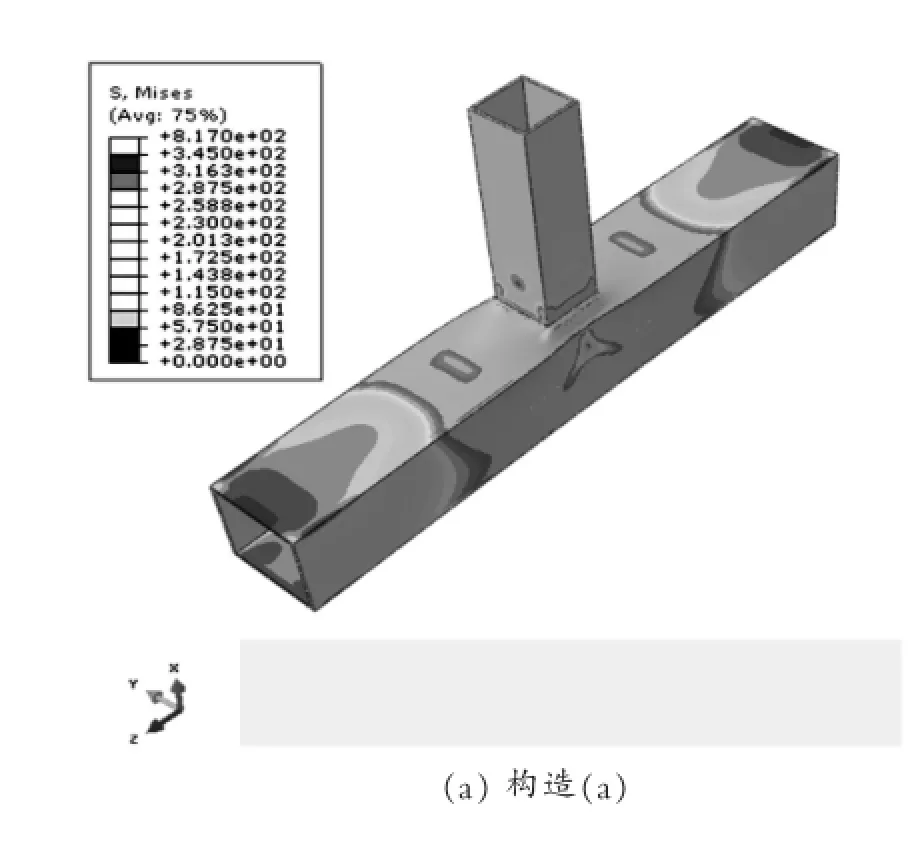
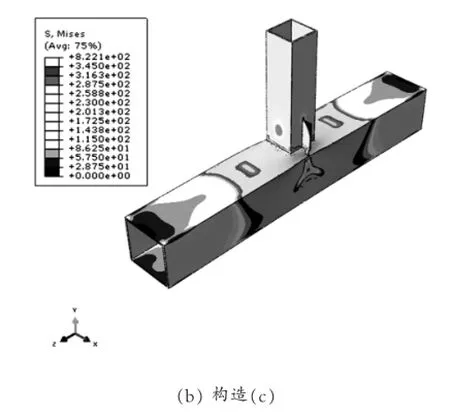
图3 弹塑性分析节点应力云图

计算可知，对材料模型进行修改后（从理想弹性模型更改为理想弹塑性模型），节点受力有了较大变化，特别是最大应力有所改变，（a）型节点、（c）型节点的最大应力值分别变为：817.0MPa、822.1MPa。

输出（c）型节点的弹性分析结果与弹塑性分析结果的力-位移曲线，如图4所示。在弹性区域，两种模型都保持在弹性阶段，力-位移曲线保持线性增长（忽略此时较小的几何非线性影响）；在弹塑性区域，即部分区域应力值达到规定的屈服强度345MPa时，弹性模型仍然保持线性增长，弹塑性模型可以通过应力重分布进行调整，继续承载，直至达到规定荷载值900kN。

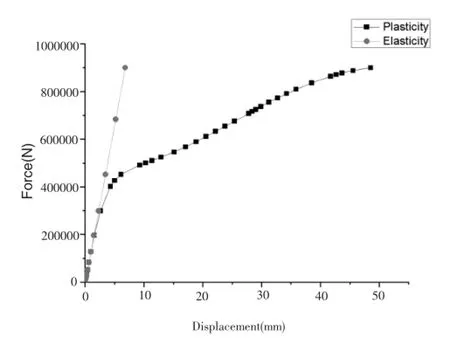
图4 （c）型节点的弹性、弹塑性力-位移曲线图

根据管节点破坏准则，当有明显屈服点时，采用极限荷载破坏准则，以极限荷载作为极限承载力；当无明显屈服点时，采用极限变形准则，通过限制变形来确定其极限承载力；当有试验对照时，采用可见裂纹准则，即出现可见宏观裂纹时确定其为极限承载力。

如上所述，本文所述节点无极限荷载点亦无法通过宏观裂纹确定其极限荷载值，故根据其极限变形（3%D）来确定其极限荷载值，取顶点位移为9mm时对应荷载为节点极限承载力，则（a）型节点、（c）型节点对应的极限荷载值分别为：349.6kN、487.3kN。

根据规范所列公式，对Q345钢材制作的T型钢管节点极限承载力设计值进行验算，如下所示：

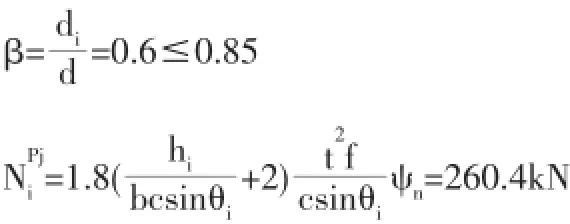
即规范所得极限承载力设计值为260.4kN，有限元模型分析无加劲肋板、有加劲肋板构造的极限承载力是规范设计值的1.34～1.87倍。分析其原因，一是规范所规定的设计值考虑了安全系数的影响，因此相对有限元模型的极限承载力而言有安全冗余；二是规范考虑节点应始终保持在弹性范围，塑性变形应有所控制，因此仅考虑弹性极限状态，而有限元模型所对应位移9mm已进入塑性阶段，因此其值相对规范设计值为大。

4 总结

基于ABAQUS通用有限元软件对工程中某T型方管节点在无加劲肋板、纵向加劲肋板、横向加劲肋板三种形式下的弹性模型以及理想弹塑性模型进行了分析比较，可知：

（1）在弹性模型下，纵向加劲肋板对节点性能的影响较小，而横向加劲肋板可以使节点应力集中现象得到有效缓解，因此在工程实际中优先考虑采用横向加劲板布置；

（2）在理想弹塑性模型下，无加劲肋板模型弹塑性分析极限承载力较小，与规范设计承载力相比较，弹塑性模型通过位移控制得到的极限承载力存在1.34～1.87倍的安全冗余，符合工程实际要求。

[1]沈祖炎，陈扬骥，陈以一.钢结构基本原理[M].北京：中国建筑工业出版社，2000：108.

[2]中华人民共和国建设部.GB50017-2003钢结构设计规范[S].北京：中国计划出版社，2003.

[3]王伟，陈以一，赵宪忠.钢管节点性能化设计的研究现状与关键问题[J].土木工程学报，2007，40（11）：1-8.

[4]武振宇，张耀春.直接焊接T型钢管节点性能的试验研究[J].钢结构：1992（2）：36-40.

责任编辑:孙苏，李红

Analysis on Mechanical Behavior of T-shaped Square Tubular Joints Reinforced by Different Kinds of Stiffener Plates

This paper performs a numerical analysis on the mechanical behavior of T-shaped square tubular joints models reinforced by no stiffener plate, longitudinal and transverse ones with ABAQUS finite element software,and the results show that the transverse stiffener plate can effectively ease stress concentration.In addition,an ideal elastic-plastic model is adapted to compare the joints,and considerable differences are found.Compared with bearing capacity under normal design codes,the ultimate bearing capacity of the elastic-plastic model obtained by displacement control has certain redundancy.

squared tubular T-joints;stiffener plate;elastic-plastic model;stress concentration

TU323.3

A

1671-9107（2017）05-0058-03

10.3969／j.issn.1671-9107.2017.05.058

2017-02-21

牛宇辰（1992-），男，安徽合肥人，研究生，主要从事混凝土结构耐久性方向研究。