基于最小误差准则的加速退化数据优化处理方法
2017-06-01成克强李小兵潘广泽李锴王远航丁小健
成克强,李小兵,潘广泽,李锴,王远航,丁小健
(1.工业和信息化部电子第五研究所,广东广州510610;2.广东省电子信息产品可靠性技术重点实验室,广东广州510610;3.广东省工业机器人可靠性工程实验室,广东广州510610)
基于最小误差准则的加速退化数据优化处理方法
成克强1,2,李小兵1,2,潘广泽1,3,李锴1,王远航1,丁小健3
(1.工业和信息化部电子第五研究所,广东广州510610;2.广东省电子信息产品可靠性技术重点实验室,广东广州510610;3.广东省工业机器人可靠性工程实验室,广东广州510610)
针对加速退化数据处理过程中存在的拟合误差问题,提出了基于最小误差准则的伪失效寿命预测方法和寿命统计过程中的多寿命分布优选方法,分别针对常用的退化模型和威布尔、指数分布、对数正态分布3种寿命分布模型,提出了退化数据优化处理方法,并用实例对该优化方法的有效性进行了分析。
加速试验;性能退化;可靠性;数据优化
0 引言
随着高可靠、长寿命复杂系统的出现,加速退化试验技术逐渐地受到了人们的关注,如何利用产品的性能参数在试验过程中的变化情况来预测产品的可靠性水平,节约试验时间和成本,是高可靠、长寿命系统可靠性试验中面临的难题之一[1-2]。试验数据处理作为加速退化试验最重要的环节,是关系到整个试验结论正确与否的关键。在进行退化数据处理时,通常采用数学模型对退化数据的变化趋势进行拟合,并在一定的阈值下,判定产品的伪失效寿命,利用经验模型对伪失效寿命数据进行统计建模,最终得出产品在某应力水平下的寿命分布模型和特种寿命[3-4]。然而,在实际的试验过程中,受到测试手段、测试成本等因素的限制,导致测试数据的量级较小,在进行数据拟合的过程中容易出现多种退化模型和多种寿命分布模型均能满足要求的情况,导致数据分析结果产生差异。基于此,本文拟提出一种基于最小误差准则的加速退化数据优化处理方法,通过模型优选的方法,选择拟合误差最小的处理方法,从而提高数据处理精度,使分析结果更加准确。
1 加速寿命试验与加速退化试验
加速试验作为解决高可靠、长寿命产品可靠性评估的重要试验手段,被广泛地应用于可靠性工程领域[5-6]。加速试验按其类型可分成定性加速试验和定量加速试验两类。其中,定性加速试验以开展产品的定性分析为主要目标,包括高加速寿命试验和高加速应力试验两类;定量加速试验以获得产品的可靠性指标为目标,主要包括加速寿命试验和加速退化试验两类。
根据产品丧失规定功能的形式,可以将产品的失效分成突发型失效和退化型失效两种类型。若产品在以往的工作或存储过程中,一直保持或基本保持所需要的功能,但在某一瞬间,这种功能突然完全丧失,则称这种现象为突发型失效;若产品在以往的工作或存储过程中,其功能随时间的延长而逐渐地缓慢地下降,直至达到无法正常工作的状态,则称此种现象为退化型失效。突发性失效和退化型失效示意图如图1-2所示。
一般而言,加速寿命试验主要针对突发型失效模式进行分析,而加速退化试验主要针对退化型失效模式进行分析。
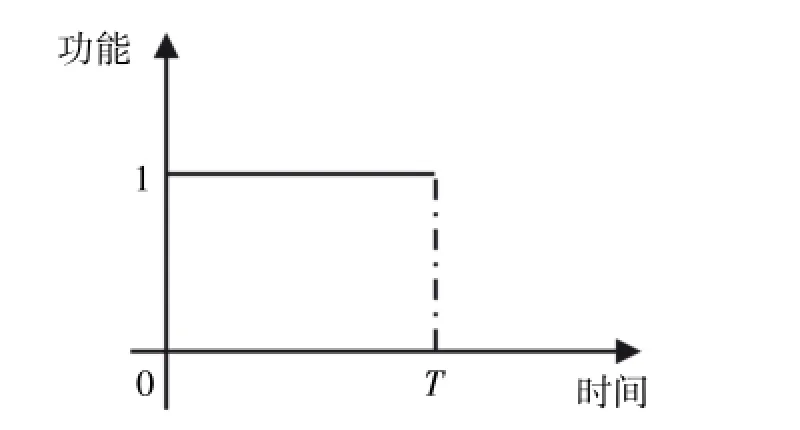
图1 突发型失效示意图

图2 退化型失效示意图
2 加速退化数据优化处理方法
2.1 基于最小误差准则的性能退化模型的建立
在恒定试验应力Si下,若样品j退化型失效的退化量随时间的变化轨迹(即理论退化轨迹)为Dij(t),则退化量的测量值可表示为:
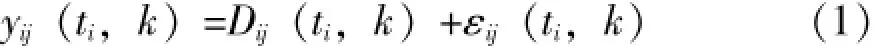
式(1)中:yij(ti,k)——Si应力下第k次测量时间ti,k的测量值;
εij(ti,k)——相应的测量误差,相互独立且服从正态分布,即εij~N
理论退化轨迹Dij(t)一般可采用以下几种线性(或变换后呈线性)模型进行拟合:
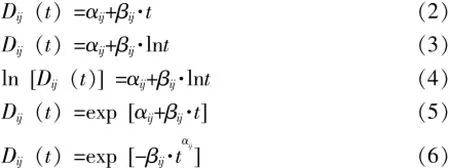
式(2)-(6)中:αij、βij——退化模型的未知参数。
性能退化模型求解可采用极大似然估计和最小二乘估计方法,并应用残差平方和最小准则选择最优模型。
2.1.1 性能退化模型的极大似然估计方法
设总体的分布密度函数为f(x,θ),其中,θ为待估参数,从总体中得到的一组样本,其观测值为(x1,x2,…,xn),抽样得到这组观测值的概率让其概率达到最大,从而求得θ的估计值设:

L(θ)为θ的似然函数。对其求极大值,得到参数θ的估计值。有时也采用似然函数的对数1nL(θ),并将其称为θ的对数似然。
2.1.2 性能退化模型的最小二乘估计方法
在x-y直角坐标系中,根据n个观测数据{xi,yi},i=1,2,…,n,按要求配出一条直线,即:

使得该直线与各个点{xi,yi},i=1,2,…,n的偏差平方和达到最小。
回归直线与各个观测值的垂直偏差记为δi=yi-(a+bxi),以E代表垂直偏差平方和,用数学公式可表示为:
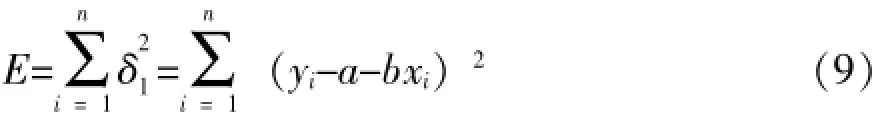
对上式中的a,b分别求偏导,并令其等于0,解方程组,得:

2.1.3 残差平方和最小准则
残差平方和通常表示在拟合过程中产生的随机误差效应,残差平方和越小,数据拟合效果越好,数据处理精度越高。由于残差平方和评估方法简便、有效,因此,此次将其选作为退化模型的优选准则。
设试验观测值为{xi,yi},以yi为因变量,残差平方和的计算方法为:

在入选的退化模型中,可选择残差平方和最小即为最优。
2.2 基于最小误差的伪失效寿命分布模型优选
对伪失效数据进行建模时,经常会出现多个模型均能对同一批数据进行拟合且能够通过单个模型的拟合优度检验的现象,因此,如何从多个通过拟合优度检验的分布模型中挑选出最好的分布模型,是保证评估结果准确与否的关键。到目前为止,在工程应用中尚无统一的优选方法,一般结合产品的实际需求,根据需要设置优选准则。
模型优选方法的基本思想是通过设置判断准则对通过拟合优度检验的各个模型进行筛选,选择出最优的模型。常用的筛选标准有:误差极差最小、误差变异系数最小、误差方差最小、最大偏差最小、累积分布函数平均误差最小和概率密度函数平均误差最小等。
在ti时刻,设产品可靠性基本函数的观测值为拟合后所得值为,有k个模型入选,对所得的失效数据t1<t2<…<tr,则各筛选标准为:
a)误差极差最小

b)误差变异系数最小

c)误差方差最小

d)最大偏差最小

e)函数平均误差最小

f)概率密度函数平均误差最小


式(18)中:f(x)——估计出的概率密度函数;
g(t)——拟合所得的概率密度函数;
a,b——评估区间。
g)极大似然函数最大
设产品寿命分布采用极大似然估计,其极大似然函数为Li,极大似然函数最大可定义为:

3 案例分析
某产品的敏感应力为温度,在3组应力条件下开展加速退化试验,共13组样品,其性能敏感参数在各个加速应力条件下的数值如表1所示,失效阈值为8.7。根据退化轨迹,选取线性退化模型、指数函数退化模型、幂函数退化模型、对数函数退化模型、Gompertz退化模型和Lloyd-Lipow退化模型等常用函数进行拟合。13组样品的退化数据拟合效果如表2所示。从分析结果可知,指数函数退化模型为最优模型。再利用外推方法求解出每个样品到达失效阈值的时间,即伪失效寿命。分别利用两参数威布尔分布、对数正态分布和指数分布进行统计建模,并选择单一准则中的极大似然函数为优选对象,计算结果如表3所示。通过优选结果可知,最优的伪失效寿命分布模型为对数正态分布模型。
若按照拟合精度最低的Gompertz退化模型,以Gompertz退化模型所得到的伪失效寿命为基础,并进行寿命统计建模,若选择寿命拟合优度的分布类型为参照,选择累积分布函数为分析对象,则拟合前后对比如图4所示。

表1 性能参数测试值
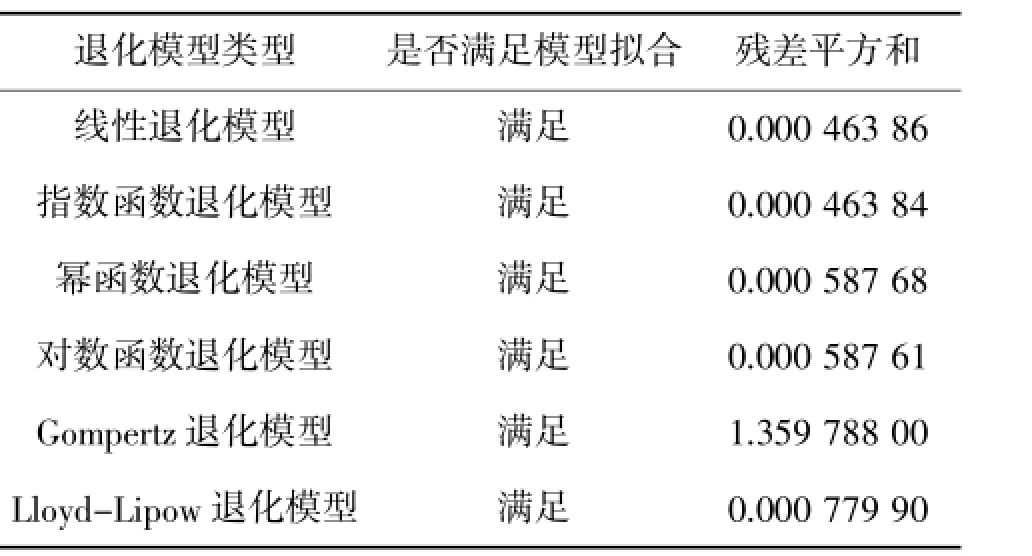
表2 退化模型拟合效果

表3 伪失效寿命分布模型优选

图4 优化前后累积分布函数
通过图4可以看出,优化前后数据处理结果的差异较大,优化效果明显。
4 结束语
本文提出了一种基于误差最小准则的退化数据处理方法,该方法首先采用误差最小原则实现对性能数据的退化模型的优选,并以最优的退化模型为基础,得出产品的伪失效寿命;其次,在进行伪失效寿命时间统计建模时,采用误差最小原则对通过符合性检验的多个寿命模型进行优选,最终选择误差最小的统计模型作为寿命分布模型,实现对试验数据的分析处理。实验分析表明,在进行退化数据处理时,采用误差最小准则进行优化处理后的结果与未优化的结果相比,差异明显,优化方法有效。
[1]吕春明,梁红卫,张春华,等.加速可靠性试验技术及其应用[J].电子产品可靠性与环境试验,2007,25(3):46-49.
[2]陈武广.电子产品高加速寿命试验方法[J].机械工程师,2015(7):145-146.
[3]尤琦,赵宇,胡广平,等.基于时序模型的加速退化数据可靠性评估[J].系统工程理论与实践,2011,31(2):328-332.
[4]黄爱梅,郭月娥,虞健飞.基于加速退化数据的航空液压泵剩余寿命预测技术研究[J].机械设计与制造,2011(1):154-155.
[5]胡湘洪,丁小健,李小兵,等.石英加计伺服电路加速退化数据处理方法研究[J].电子产品可靠性与环境试验,2016,34(2):1-6.
[6]邓爱民,陈循,张春华.基于加速退化数据的可靠性评估[J].弹箭与制导学报,2006,26(2):808-815.
Accelerated Degradation Test Data Optimization Analysis Method Based on Minimum Deviation Criterion
CHENG Keqiang1,2,LI Xiaobing1,2,PAN Guangze1,3,LI Kai1,WANG Yuanhang1,DING Xiaojian3
(1.CEPREI,Guangzhou 510610,China;2.Guangdong Provincial Key Laboratory of Electronic Information Products Reliability Technology,Guangzhou 510610,China;3.Guangdong Provincial Engineering Laboratory for Reliability of Industrial Robot,Guangzhou 510610,China)
In order to solve the fitting error in the process of accelerated degradation data handling,a pseudo failure life prediction method based on the minimum error criterion and the multi-life distribution optimal selection method during life statistics process are put forward.Andthe degradation data optimization method is proposedaiming at the common degradation model and the three life distribution models of Weibull distribution,exponential distribution and logarithmic normal distribution.Besides,the effectiveness of the optimization method is evaluated through an example.
accelerated test;performance degradation;reliability;data optimization
TB 114.3
A
:1672-5468(2017)02-0010-05
10.3969/j.issn.1672-5468.2017.02.003
2016-09-22
2017-03-22
成克强(1983-),男,湖南永州人,工业和信息化部电子第五研究所科技处工程师,主要从事可靠性技术、数据优化等方面的研究工作。
