动车组车体车门设计及模态性能改进

张军，王建华，兆文忠

(大连交通大学 交通运输工程学院，辽宁 大连 116028)*

动车组车体车门设计及模态性能改进

张军，王建华，兆文忠

(大连交通大学 交通运输工程学院，辽宁 大连 116028)*

车体模态频率是影响车体性能的重要动力学参数，车体模态计算和分析是设计过程中的重要内容.建立了城际动车组铝合金车体有限单元模型,用有限单元法计算了车体模态，分析了车门位置、车门高度、车门宽度、中间车门与窗口之间的距离对车体模态频率的影响.研究表明:车门位置、高度均对车体模态有较大影响，两端车门向车体两端移动可以提高车体一阶垂弯模态频率，降低中间车门高度可以明显提高车体一阶扭转模态频率.通过重新布置车门位置、修改车门尺寸及门框结构，在保证车体重量不变的情况下使车体模态频率得到了较大提高.

动车组；铝合金车体；有限元法；车门；模态频率

0 引言

高速动车组车体主要采用拉伸铝型材, 这种材料结构具有轻量化、耐挤压等多种特点,越来越多的应用在高速动车组上，用这种型材构建的车体为筒形整体承载式结构，既将底架、侧墙、端墙壁及车顶牢固地组成为一整体，成为开口或闭口的箱形结构，车体各个部分均能承受载荷的车体结构[1- 3].车体承受垂向、纵向拉伸、纵向压缩、扭转、气密、各种组合工况的综合作用.在复杂载荷的综合作用下要求车体满足强度、刚度、模态等相关标准要求.尤其车体模态需要满足相关标准要求，即纯空车一阶垂弯模态频率要大于17 Hz的要求，整备车一阶垂弯模态频率要大于10 Hz的要求[4- 5].车体模态频率是车辆最重要的动力学参数之一，不合理的模态参数，不但影响车辆运行中的振动特性，而且影响车辆的乘坐舒适性[6- 7].文献[8]通过计算和试验分析了车体不同配重对车体一阶垂弯模态频率的影响，研究表明随着配重的增加车体一阶垂弯模态频率降低；文献[9]分析了车体不同位置板厚度对模态频率的影响，分析了车体前三阶模态频率随不同位置板件厚度的变化规律，为改进车体模态设计提供了借鉴和参考.

本文针对某城际动车组车体模态频率低的问题，通过改进车门位置和尺寸，分析了车体前三阶模态频率随车体位置、车门高度、车门宽度、门框结构形式对车体模态频率的影响，通过重新布置门的位置和尺寸使车体模态频率得到了提高.

1 结构模态分析基本理论

车体模态频率和振型是车体最重要动力学参数，计算车体模态频率和振型是车体结构设计过程中的重要内容，计算和分析的目的是验证车体模态是否与激励频率或者其它结构存在共振，并采取相应性控制措施.模态计算一般使用有限单元法，有限单元法是最广泛使用的数值方法.车体结构经过有限单元法离散后，可以得到用矩阵表示的车体动力方程，表示为x

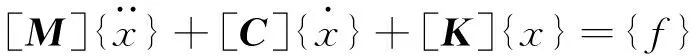
(1)

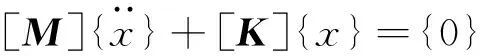
(2)

车体自由振动为简谐振动，即向量{x}可以表示为{x}={X}eiωt,{X}为车体振型向量，{X}实际上为车体振动幅值向量，ω为车体振动角频率；代入式(2)，得车体振动的特征方程为

(3)

求解上式可以得到车体各阶模态对应的特征值ωi，则车体模态振动频率为fi=ωi/2π.

2 车体有限单元模型及车门修改方法

为了快速实现对车门位置及尺寸的修改，采用参数化建模方法，利用ANSYS的参数化建模语言APDL建立车体中面参数化几何模型[10]，将车体中面模型导入到HYPERMESH建立有限单元模型，这种方法综合利用了ANSYS能快速建立车体不同结构参数的中面模型和Hypermesh高性能的有限网格生成功能，实现了快速建立具有不同位置和尺寸车门的车体有限单元模型，提高了建模效率.参数化建立的初始车体中面模型如图1所示.模型中将车门位置车寸、车门高度车寸、车门宽度等尺寸设置为可修改的参数.

图1 参数化车体中面模型

初始车体有限单元模型如图2所示，车体共划分493 721个有限单元，采用三角形和四边形

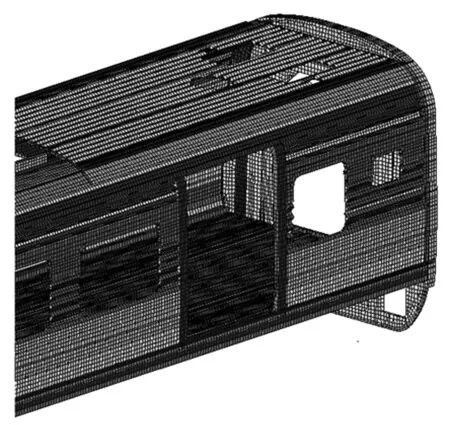
(b)局部有限元模型

单元，以四边形单元为主，单元边长约为50 mm.由于对车门位置及尺寸进行了修改，重新建立的模型中有限单元的数量发生了较小变化，但总体数量在493 000左右.

3 初始车体模态计算

车体模态计算用整车模型，初始车体前4阶模态频率被列在表1中，前4阶振型如图3所示.

表1 模态振型及频率

(a)一阶菱形 (b)一阶垂弯

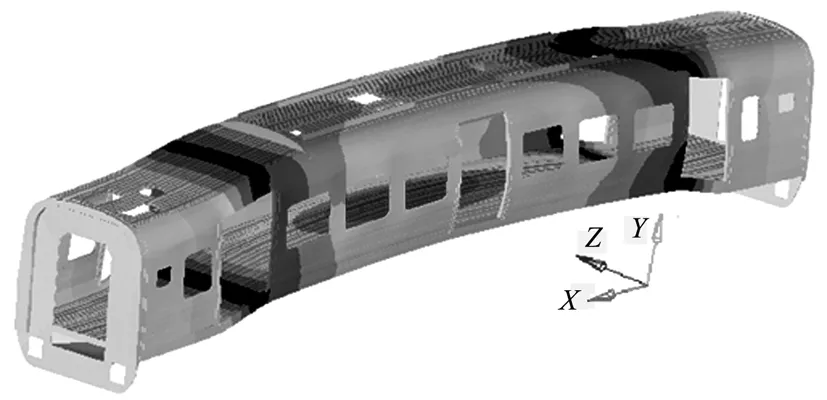
(c)一阶扭转 (d)一阶呼吸

图3 车体前4阶模态振型

表1表明,该车铝合金车体一阶垂弯模态频率为14.85 Hz,小于17 Hz的要求,需要通过结构修改使其提高,以满足相关要求.

4 车门对车体模态影响分析

4.1 车门位置对模态频率的影响

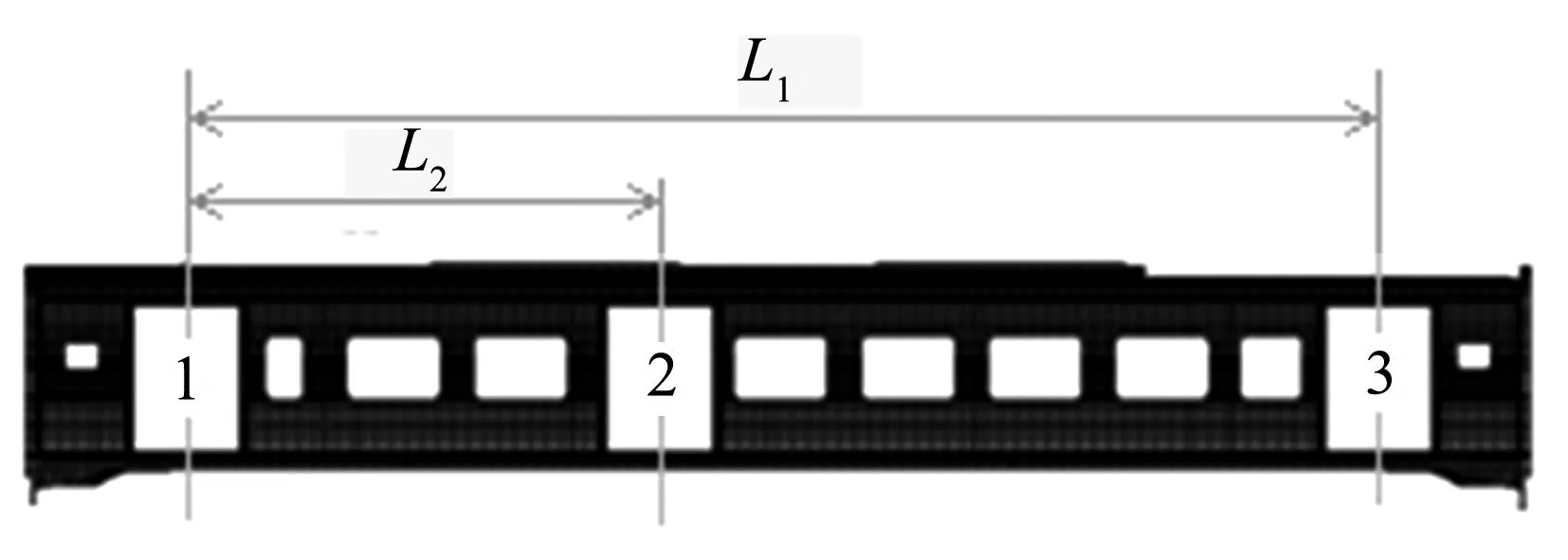
车体侧墙结构及车门如图4所示，图4和图1表明该车体有3个车门，图1中车门位置为车门初始位置，车门1、车门3在两端，距离为L1=16 548.8mm，车门2在中间，定位车门2的L2=8 273.8mm.为了研究车门位置对车体模态频率的影响，考虑了两个方案，一是只将车门1、3对称向车体两端移动，移动后L1=19 160.6mm，即将车门1、3之间距离增大2 611.8mm；二是同时在移动车门1、3的同时，将车门2向左侧移动，L2由原来的8 273.8mm减小到7 606.9mm.修改后车门位置如图4所示.车门位置修改后模态频率分别列在表2和表3中.

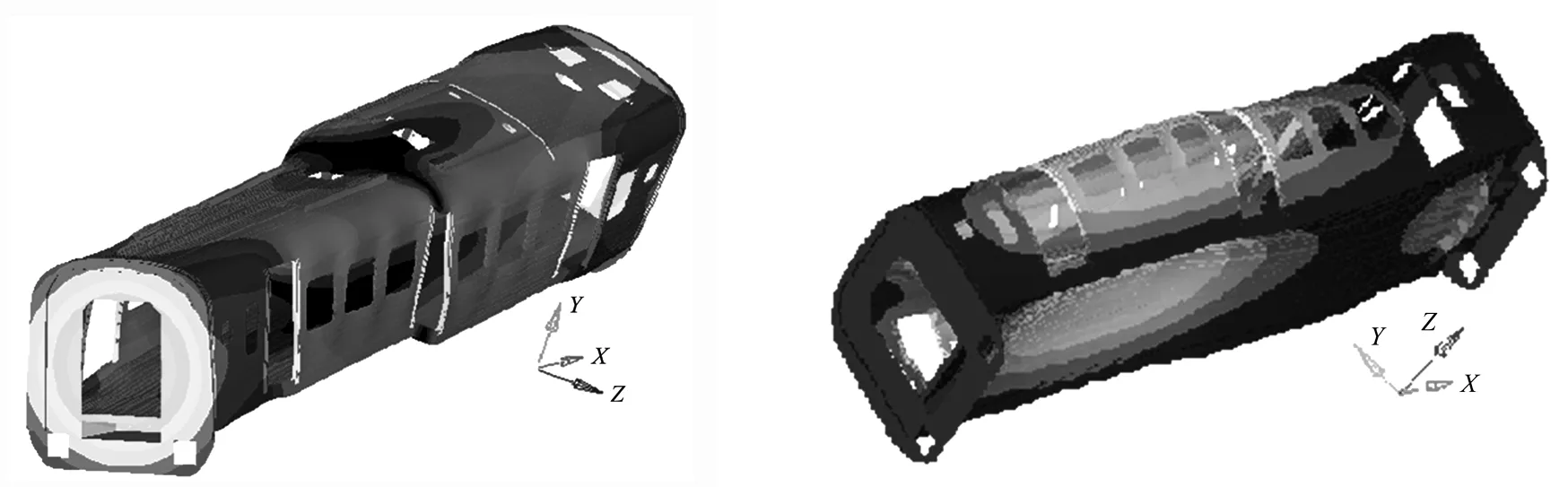
图4 车门位置

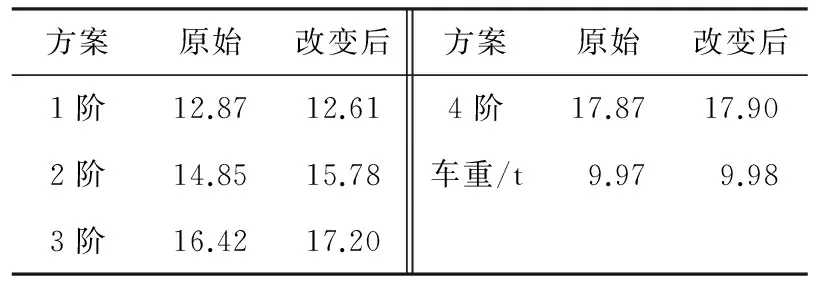
方案原始改变后方案原始改变后1阶12.8712.614阶17.8717.902阶14.8515.78车重/t9.979.983阶16.4217.20

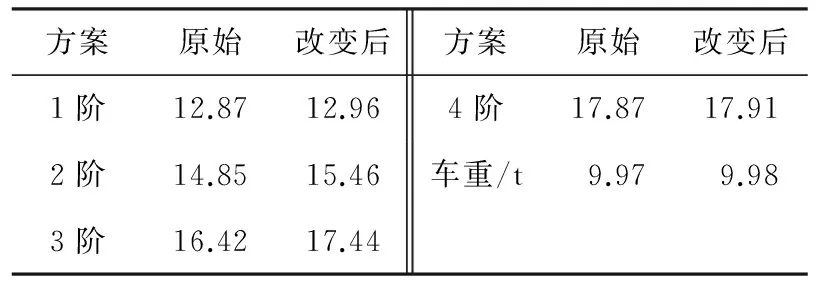
表3 三个车门同时改变时车体模态频率 Hz

表2、表3表明，将两端的车门同时向外侧移动可以大幅提高车体的二阶和三阶模态频率，但是会导致一阶模态频率小幅减小.由表2数据可以看出，二阶模态频率提高了0.93 Hz，三阶模态频率提高了0.78 Hz，车体重量几乎没有变化；将三个门同时移动对一阶到三阶的模态频率都有所提升，但是对二阶模态频率的提升幅度不如单独移动两个车门的方案大.对4阶模态频率影响相对较小.

4.2 车门高度对车体模态频率的影响

车门高度主要是修改中间车门的高度，该动车组车体由于设置了中间门3导致车体中部刚度较低，车门1、2的尺寸对车体模态的影响可以忽略，图5为车门3修改方案及尺寸示意图.主要研究了四个方案，一是在只移动车门1、3的基础上降低车门2的高度H，由原来的2 061.6mm降低到1 903.3mm；二是在只移动车门1、3的基础上，在车门2(中间车门)上部增加门框结构，门框结构的断面如图6所示；方案三和四分别是在3个车门同时移动的基础上降低车门2高度和增加车门2上面的门框结构.修改后车体模态频率被列在表4中.

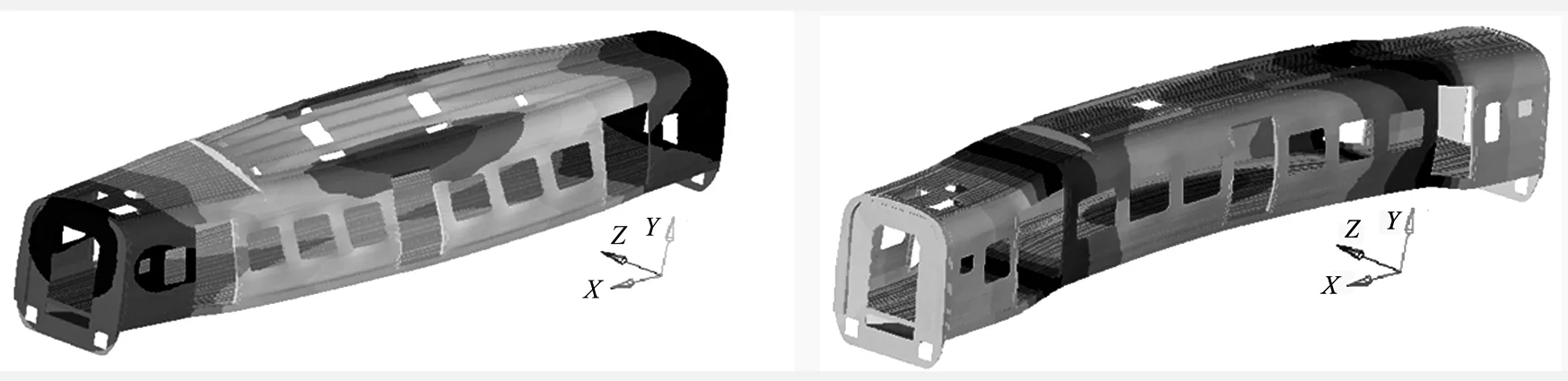
图5 车门3修改方案及尺寸

图6 增加的门框断面图

方案原始12341阶12.8712.6112.6312.9512.952阶14.8515.7815.7815.5715.573阶16.4217.6717.7517.8117.814阶17.8718.1017.9518.2818.28车重/t9.9710.0110.0110.01710.017

将中间门高度降低，无论是单纯降低门的高度，还是通过加横框的方法降低，对车体的一阶和二阶模态频率都几乎没有影响，但是会提高三阶模态频率.但是该方法会导致车体的三阶模态的振型发生改变，即三阶扭转模态频率提高，使扭转模态出现在第4阶模态，而原来的第4阶呼吸模态现在成为第3阶模态.可见降低车门高度或者增加车门2上部的门框结构可以显著提高车体扭转刚度，使车体1阶扭转模态频率得到明显提高.

4.3 车门宽度对模态频率的影响

将图5中的车门2宽度W减小100mm，由原来的1 500mm减小到1 400mm，在车门1、3向两端移动、中间车门位置不变基础上对车门2宽度进行修改，修改后车体模态频率如表5所示.

表5 车门宽度修改后车体模态频率 Hz

表5表明，减小中间车门的宽度可以提高车体扭转刚度，使扭转模态频率明显提高，但对1、2阶模态频率影响较小.

4.4 车门与车窗间距对模态频率的影响

为了研究车门与车窗间距离及车窗与车窗间距离对车体模态的影响，将图7中椭圆内的结构加宽，具体修改方法如下：将车窗1、2右侧边向左移动100 mm，将车窗3、4的左侧边向右移动100 mm.修改是在车门1、3向两端移动、车门2不变、车门宽度和高度均不变的基础上进行.修改后车体模态频率被列在表6中.

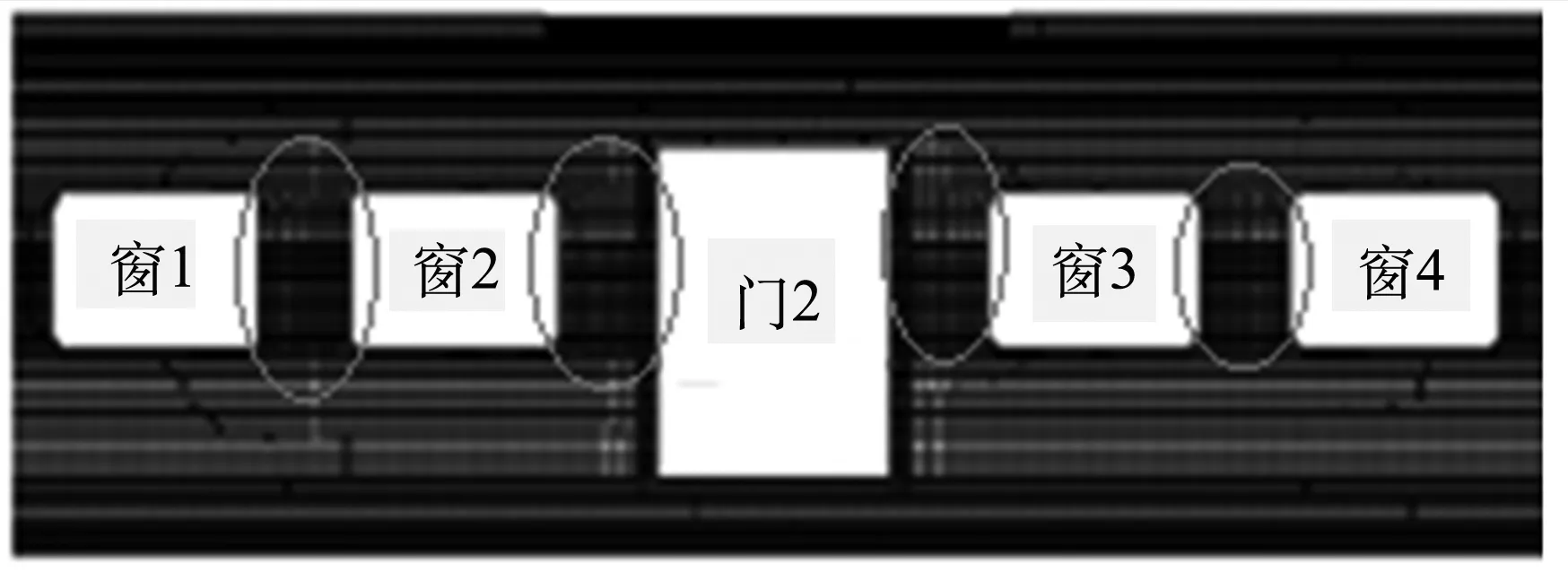
图7 中间车门及车窗间布置

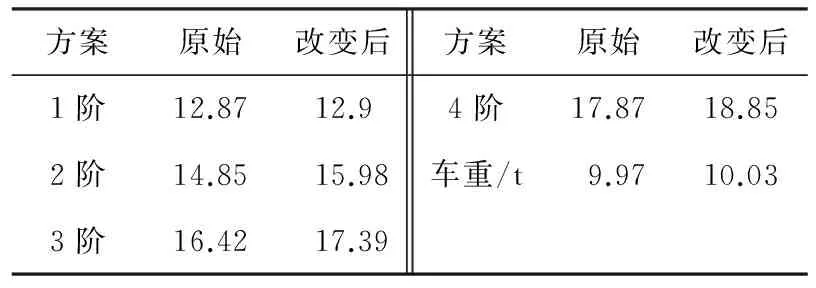
方案原始改变后方案原始改变后1阶12.8712.94阶17.8718.852阶14.8515.98车重/t9.9710.033阶16.4217.39

表6与表2比较表明， 将车门与车窗间距及车窗与车窗间增加后，车体前4模态频率均有提高，一阶垂弯模态频率提高了0.2 Hz，3、4阶模态频率分别提高了0.19 Hz和0.95 Hz，取得了较好的效果.

5 结论

本文建立了某城际动车组铝合金车体车参数化有限单元模型，计算了车体模态，计算分析了车门位置、尺寸、结构等改变对车体模态频率的影响，得到如下结论 ：

(1)将两端车门向车体两端移动可以显著提高车体1阶垂弯模态频率，在不增加车体重量的前提通过移动两端车门使车体1阶垂弯模态频率提高了0.93 Hz；

(2)降低车体中间车门高度或者增加车门顶部门框结构可以显著提高车体扭转刚度，因而提高了车体1阶扭转模态频率，1阶扭转模态原来是车体的第3阶模态，通过降低车门高度使车体扭转模态变成了车体的第4阶模态，1阶扭转模态频率提高了大约1 Hz，但降低中间车门高度对1、2阶模态频率影响较小；

(3)减小中间车门宽度同样对提高车体1阶扭转模态(第3阶模态)效果较好，对提高车体1、2阶模态效果 较小；

(4)增大中间车门与车窗及车窗与车窗间距可以提高车体第2阶(1阶垂弯)、第3阶(1阶扭转)和第4阶(1阶呼吸)模态频率，对提高车体第3阶和第4阶模态频率效果较好；

(5)通过对车门位置、车门尺寸及结构等的重新设计，结合车体截面修改、优化设计等措施，提高了车体模态频率，尤其在保证车体重量不增加的情况下使纯铝合金车体1阶垂弯模态频率满足了大于17 Hz的要求，提高了车体性能.

[1]郑文波，刘东军，田新莉．铝合金型材在CRH3型动车组车体中的应用[J]．金属加工，2011，23：19- 22．

[2]谢素明，王思阳，高阳.高速动车组铝合金车体性能的深入研究[J].大连交通大学学报,2014,35(6):14- 18.

[3]何广忠,刘长青.动车组铝合金车体材料的发展 与选型分析[J].焊接，2015(1)：13- 16.

[4]平学成,王先亮,朱韶光,等.B型地铁铝合金车体工作模态分析[J].铁道机车车辆,2015,35(1):115- 117.

[5]李伟，缪炳荣，张立民.高速列车车体模态特性与结构尺寸敏度关系研究[J].铁道机车车辆,2015,35(5):1- 4.

[6]宫岛,周劲松,孙文静,等.铁道车辆弹性车体垂向运行平稳性最优控制[J].同济大学学报,2011,39(3):416- 420.

[7]罗光兵,曾京.基于弹性结构的轨道车辆振动分析[J].机械设计与制造,2013(5):67- 73.

[8]张远亮，张立民，张艳斌,等.车体配重对车体1阶垂弯频率的影响分析[J].铁道机车车辆,2015,35(1):51- 53.

[9]于金朋,张卫华,孙帮成.高速车体结构参数对 车体模态频率的影响分析[J].铁道学报,2015,37(9):32- 37.

[10]张军,李永华，王悦东,等.基于APDL高速铝合金车体参数化建模[J].大连交通大学学报,2009,33(3):14- 18.

Research on Door Design and Modal Performance Promotion for EMU Bodwork

ZHANG Jun,WANG Jianhua,ZHAO Wenzhong

(School of Traffic and Transportation Engineering,Dalian Jiaotong University,Dalian 116028,China)

A finite element model of a EMU bodwork is established, and the bodywork modals are extracted by using finite element method. The changes of modal frequencies along with the door position, door height, door width and distances between doors and windows are analyzed. The results show that the door position and door height have significant effect on the bodwork modal frequencies. The first order bending mode frequency can be increased by moving the end doors to the vehicle ends, and the first order torsion mode frequency can be improved by reducing the height of the middle door. The modal frequencies of bodywork are well improved by making over the door position, door height and door structure, etc, and meanwhile the bodywork weight is not added.

EMU bodywork; finite element method; door; modal frequency

1673- 9590(2017)01- 0017- 05

2016- 01- 05

中国铁路总公司科技计划资助项目(2014J004-O)；牵引动力国家重点实验室开放课题资助项目(TPL1402)

张军(1964-)，男，教授，博士，主要从事车辆结构优化设计、声学仿真及噪声控制方面的研究工作E-mail:zhj@djtu.edu.cn.

A