跳出题海 提升能力
——谈谈一元一次不等式组的解法
2017-06-01江苏省南通市八一中学
江苏省南通市八一中学 李 珲
跳出题海 提升能力
——谈谈一元一次不等式组的解法
江苏省南通市八一中学 李 珲
一元一次不等式组最常见的解法是数学中最具有代表性的数形结合的思维方法。为了培养学生数形结合的思想,在教学中常常辅助以大量的练习题,在题海战术中提升学生的数学思想。初中学生集中注意力的时间不能长久,好动是他们的天性,如何才能跳出题海,又能提升能力呢?本文就通过一元一次不等式组解法的案例来诠释一个全新的教学方法。
一元一次不等式组;题海 ;数形结合
在初中学习不等式组的解集时,最常见的方法就是借助数轴,首先在数轴上将每一个不等式的解都表示出来,然后找到它们解的公共部分,这就是一元一次不等式组的解集。
一、数形结合让一元一次不等式组的解法更加简单明了
一元一次不等式组学习的课堂总是容量偏大,而且运用的数学思维又比较特殊,从而导致学生在课堂上目不暇接,大量的训练让时间比较紧张。因此应该在课堂上尽可能地减少容量,多给学生思考的时间和空间。只有学会解题规律,才能减轻学习负担。

【分析】首先分别求出两个不等式各自的解:
由 3x-1 > 2x+4,得出 x > 5;
由 3x > 12,得出 x > 4。
在数轴上分别表示两个不等式的解:

找出它们的公共部分,即x>5就是这个一元一次不等式组的解集。
通过案例证明一元一次不等式组的求解过程,数形结合的方法是初中学生最容易理解的方法,也是他们最适用的方法。
然而,在实际问题中抽象出来的数量关系的数学建模,需要对数学的概念和数学思想统一起来呈循序渐进状态。学生在学习过程中,不但要加强训练,挖掘自我解题的潜能,而且要通过“查漏补缺”和相互交流,才能提升学科素养。
二、认知规律让一元一次不等式组的解法更加顺理成章
有效的练习可以让学生茅塞顿开,所以,很多教师总是用“题海”来启迪学生的智慧,造成学生对课堂的练习望而生畏,不去思考。让学生能够积极参与学习活动,参与将不等式组变形,让学生在新情景下产生新鲜感,再通过小组交流产生互动协作感,规律就一定能够快速掌握。

在数轴上分别表示两个不等式的解:
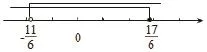
本案例需要将不等式转换为不等式组的方法来求解,但学生初次接触这类试题总有力不从心的感觉,为了解决实际问题,在课堂练习时需要由表及里,由简到繁。也就是说课堂练习设置要有一定的梯度,不要盲目采取题海战术。
三、在总结中让一元一次不等式组的解法更加入脑入心
例 3 采风旅行团共有 48 人入住长河宾馆,该宾馆一楼比二楼的客房少5间,若全部住一楼,每间4人,还剩有客人;每间住5人,还有房间不满5人。若都安排于二楼,每间3人,还剩有客人;每间住4人,还有房间住3人,该宾馆一楼有客房多少间?
【分析】这是一道应用题,考查了学生对实际问题的理解能力。若长河宾馆的一楼房间数目是 x,则二楼房间数目就是 x+5。通过房间安排人数来将文字变为数学式。
①若全部住一楼,每间 4 人,还剩有客人,则有 4x < 48;每间住 5 人,还有房间不满 5 人,说明 5x > 48。
②若都安排于二楼,每间 3 人,还剩有客人,则有 3(x+5)< 48;每间住 4 人,还有房间住 3 人,得出 4(x+5)> 48。
由①可知:x < 12,x > 9.6。
由②得出:x < 11,x> 7。
最后用数轴表示解集为:

因此解集为:9.6 < x < 11,但客房数目应是整数,故该宾馆一楼有客房10间。
该案例是不等式组在生活中的实际应用。在教学实践中发现,很多学生不能有效地将文字与数学语言联系起来,不能准确地根据题目中含有不等语言的语句找出不等关系,列出一元一次不等式组。因此,很多学生试图采用方程解决本问题,但最终事与愿违。要让学生在字里行间中找到“不等式”,必须抓住关键词,如题目中的“剩有”、“不满”等。
总之,在不等式组的解法中,“数形结合”的数学思想是最具有权威性的。这种方法需要的是学生适当的练习,而不是题海战术。课堂上的练习应该采用多种题型来激发学生学习的兴趣,让他们主动参与,积极思考、探究。无论什么样的题型,其解决问题的思路是相同的,基础知识都是一样的,即求解不等式口诀:“大大取大、小小取小、大小小大取中间、大大小小解不了。”唯有正确地培养学生的数形结合思想,才能在不等式组的解法中跳出题海、减轻负担,我们的课堂才能蒸蒸日上、欣欣向荣。
[1]苏芳 .例谈一元一次不等式组中字母系数取值的确定 [J].中学生数理化:教与学,2014(2).
[2]李双轿,王爱东 .用数轴确定一次不等式中的参数 [J].中学生数学:初中版,2015(2):12-13.
[3]李双全 .方程与不等式中考试题分析与精选 [J].中学生理科月刊:初中版,2005(Z2):29-33.
