圆锥曲线上的一个性质的探究
2017-06-01新疆大学附属中学常晓兵
数学大世界 2017年11期
新疆大学附属中学 常晓兵
圆锥曲线上的一个性质的探究
新疆大学附属中学 常晓兵
在高中选修 2-1 第二章 2.2.1《椭圆及其标准方程》中,有这样一道例题:如图 1,设点 A、B 的坐标分别为(-5,0),(5,0)。直线PA,PB相交于点P,且它们的斜率之积是求点P的轨迹方程。

图1
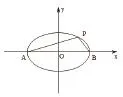
图2

探究二:如果我们将左右两个端点换成上下两个端点,上述探究结论是否成立?
在探究一中将 A(-a,0),B(a,0)两点换成 C(0,-b),D(0,b)。P(x,y)为椭圆上异于 C,D 两点的任意一点(如图 3),试证

通过探究,当左、右端点换成上、下端点时,结论仍然成立。
探究三:从探究一和二中可以看出 A,B两点和C,D两点分别是椭圆在x轴与y轴上的端点。

图3
A,B 关 于 中 心 对 称,C,D 关 于 中心 对 称。 猜 测 若取 两 个 点是椭圆上任意直径的两个端点(如图4)。证明

将⑥⑦代入⑤中,得:可知结论成立。

探究四:由于该结论在椭圆中验证成立,那么在双曲线中该结论是否也成立呢?于是,我们继续探究。

图4

图5

由双曲线方程知:


通过以上探究,可知对于椭圆、双曲线都符合这个结论,对于圆是否也成立呢?
如图 6,设过圆 O 圆心的直线交圆于 P1、P2两点,显然即可以归纳为:平面内与两定点的连线的斜率的乘积为定值的点的轨迹可以是:圆、椭圆、双曲线。
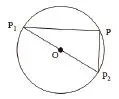
图6
