元胞自动机在模拟细胞行为方面的应用

2017-06-01李向阳崔甜甜

中国生物医学工程学报 2017年2期

关键词：元胞自动机时刻

李向阳孙亮崔甜甜

(苏州大学医学部放射医学与防护学院,江苏苏州 215000)

元胞自动机在模拟细胞行为方面的应用

李向阳孙亮*崔甜甜

(苏州大学医学部放射医学与防护学院,江苏苏州 215000)

在生物细胞生长机理以及莫诺德微分方程模型的基础上，推导出生物细胞生长以及底物消耗的微分方程，并基于此建立模拟生物细胞生长的元胞自动机模型(CABCGM)。CABCGM采用二维细胞自动机作为细胞的生长空间，采用Moore型邻域作为细胞的邻居规则，其演化规则根据细胞的生长机理和推导出的动力学微分方程设计。在建立元胞自动机模型的前提下，以Matlab为开发工具来实现模型编程，并进行仿真实验。仿真结果表明，利用元胞自动机建立的生物细胞的生长模型与实际微分方程细胞的生长曲线比较吻合(尤其在前期时间段)，故元胞自动机能较好地描述细胞生长的演化行为。

元胞自动机模型；生物细胞；细胞行为

引言

对于生物细胞生长动态的描述模型，最常用的是纯数学模型。纯数学模型一般为非线性动力学微分方程[1-2]，通常是在理想情况下通过理论推导得出来的，是一类确定性的机理模型。非线性动力学微分方程的这一特点有些与生物细胞生长的随机性特点相悖，当生物非线性系统的复杂性增加，以及求解微分方程或计算数值的过程变得越来越无望时，元胞自动机的优点就突显出来，它是非常灵活有效的建模工具。

上世纪80年代末，Christopher Langton提出了人工生命，并指出生命系统的实现形式有多种，除已知的碳水化合物的形式，还可以利用别的物质构造出不同于自然生命的另类载体生命形式，赋予它们生命特征，使其具有进化、变异等生命现象，得出生命的普遍行为。这类的形式可以是物理的、化学的以及程序的形式等[3-7]。元胞自动机，正是从人工生命衍生出的一个分支，其单位众多、特定条件相互作用，具有量变到质变的“涌现”现象等特性，是当之无愧的复杂系统，是自然生命系统的对偶系统，为复杂系统建模、仿真和控制提供了一种理想的计算模型，其表现复杂系统的能力为细胞生长过程的建模仿真提供了新思路[8]。细胞的生长是一个复杂的生化过程，就单个细胞而言，其生物活性相对简单，但其形成的整个生化过程却表现出复杂的行为[9-10]。细胞群落与环境相互作用，发展并丰富自身结构或形态，也即自组织过程。这个过程机理复杂，动态行为多变，其演化具有多样性、随意性、不确定性以及强非线性等，说明它符合复杂系统的特征。目前，研究细胞生长建立的模型不是以复杂系统的观点建立的，所以建立的模型未能表现出复杂系统的特征，使得这类模型与细胞的生长实际存在较大的差距。

本研究基于生物细胞生长的机理和推导出的动力学微分方程，建立了模拟生物细胞生长的元胞自动机模型(cellular automata model of biology cell growth,CABCGM)，并根据设计的Matlab规则进行了编程设计，并进行了仿真实验。仿真实验结果表明，CABCGM能较好地复现动力学微分方程所描述的生物细胞生长过程，还可以使演化过程可视化。对于Matlab模拟生物细胞的研究鲜有报道，本次CABCGM的设计，是用Matlab在生物细胞领域建模的新探索。

1 实验方法

1.1 细胞生长及基质消耗的动力学微分方程的推导

现代细胞动力学的奠基人Monod为代表的众多科学工作者对各种细胞动力学模型进行了研究和建模，其中最为著名的是莫诺德方程[11-13]，即

(1)

式中：μ为比生长速率；μm为最大比生长速率；Ks为半饱和常数，其值为比生长速率等于最大比生长速率一半时的基质浓度；S为生长的基质浓度。

按照比生长速率的定义，有

(2)

联立式(1)、(2)便得到

(3)

若取足够小，则

(4)

联立式(3)、(4)便得到差分方程，即

(5)

同理，在基质消耗方面，根据碳守恒原理，S底物=X细胞+P产物+m维持，即

(6)

由于本次模拟不考虑产物的生成，故不考虑P产物项，得

(7)

同理，若取得足够小，即

(8)

联立式(3)、(7)、(8)，得到关于基质消耗的差分方程如下：

(9)

以上为细胞生长及基质消耗的动力学微分方程和差分方程的推导过程，可进一步对其中的差分方程进行理论特性统计分析，得到CABCGM与离散的生物细胞生长动力学模型在数学期望意义下是一致的结论，这对本研究构造的CABCGM具有指导意义。基于此，还可以假设细胞生长过程中的浓度最大值为Xmax，细胞浓度在T0时间内的最大变化量ΔXmax(t)，根据细胞生长机理和实验实例，设置参数后，Xmax和ΔXmax(t)可由式(3)和式(5)求出，为后面演化概率的设计做准备。

1.2 CABCGM结构设计

本次模型采用二维元胞自动机作为生物细胞生长模型，元胞自动机中的每一个元胞代表一个生物细胞，每一个元胞具有不同的状态。在元胞自动机中，生物细胞的生长演化过程就是元胞自动机各个元胞在不同状态值之间不断转化的过程。基于CA的生物细胞生长模型被定义为一个五元组，有

(10)

式中：t为离散时间；Cells为CABCGM的基本元素，即元胞；Cellspace为细胞空间；Neighborhoods为CABCGM的邻域，即演化规则的定义域；Rules为CABCGM的演化规则，规定着元胞状态的演化，是CABCGM的核心。

1.2.1 CABCGM的离散时间

对生物细胞的整个生长过程进行离散化，对于每一个离散时刻t=kT0，其中k={0,1,2，…，N}为离散时间序列，T0为离散时间间隔。

1.2.2 CABCGM细胞和细胞空间

元胞是CABCGM的基本元素，假设CABCGM的元胞是一个微小的正方形。本次模拟的是在理想情况下在直径为d=10 cm的平皿上生长的细胞，最终长出5×106个细胞，据此把每个细胞由圆形折合成正方形，得到单个细胞的边长为40 μm。整个细胞空间Cellspace={Cij|i，j∈{0,1,2,…，N}}，其中N×N为元胞空间的元胞总数。

1.2.3 CABCGM细胞邻域

CABCGM的元胞邻域是其演化规则的演化作用范围，也就是元胞演化规则的定义域。在此采用Moore型领域，定义如下：

(11)

1.2.4 CABCGM细胞状态

CA中的每一个元胞代表一个细胞，每个细胞具有不同的状态，令CA细胞Cell(i,j)在t时刻的状态为Sij(t)，取两种状态值(0和1)。其中，Sij(t)=0表示Cell(i,j)在t时刻为空或细胞死亡，Sij(t)=1表示新生细胞占据了该空格。如此，在CA模型中，细胞的生长过程就是CA各个细胞单元的状态值在0、1之间不断转化的过程。

1.2.5 CABCGM的演化规则

CA的演化规则具有局部特性，CA的每个细胞演化均依赖于与之相邻的细胞状态。也就是说，细胞下一时刻的状态只与它邻域的细胞状态有关。CA按照演化规则进行并行演化，即在任意一个离散时刻，细胞空间中所有细胞同时依据规则演化。

根据生物细胞生长机理以及推导出来的动力学微分方程，设计了CABCGM的演化规则如下：

1) IfSij(t)=0,then

(12)

式中，N(i,j,t)是t时刻CA元胞Cell(i,j)的Moore领域内细胞的个数，P0,1(i,j,t)为t时刻状态为0的元胞在下一个时刻演化为状态1的演化概率，P0,1,Thr(i,j,t)是t时刻状态值为0的细胞下一个时刻演化为1的概率阈值。

演化概率定义如下：

(13)

式中，ΔX(t)是CA模型中在t时刻的理想扩增量,ΔXmax(t)是模型的最大扩增量，L0,1是状态0元胞向状态1元胞演化的趋势系数，

P0,1,Thr(i,j,t)、L0,1根据具体培养条件和机理确定，并在仿真实验中进行必要调整。

2) IfSij(t)=1,then

(14)

1.3 仿真实验

利用Matlab仿真软件，编制CA的演化程序进行仿真实验。CA的演化程序包括下列功能：

1)利用推导公式须计算Xmax、ΔXmax，此外还需计算每一kT0时刻的细胞浓度、kT0→(k+1)T0时间段内的细胞浓度变化量ΔXmax(t)；

2)在二维状态空间上，自动描绘CA的元胞状态演化图案；

3)在每一个离散时刻kT0对CA元胞进行质量统计，并换算成CA的细胞浓度，描绘出各状态元胞随时间变化的曲线；

4)对每一kT0离散时刻CA的元胞进行质量统计，并换算成CA的细胞浓度，描绘其随时间变化的曲线。

CABCGM的活细胞质量统计方法是：将状态值1的细胞质量均视为1，因此当状态值为1的元胞数量为N1时，那么状态值1的元胞质量为N1，设CA的元胞质量换算成浓度的换算系数为α，则CA的细胞浓度C=αN1，换算系数α可在实验仿真时进行必要的调整。

2 实验结果

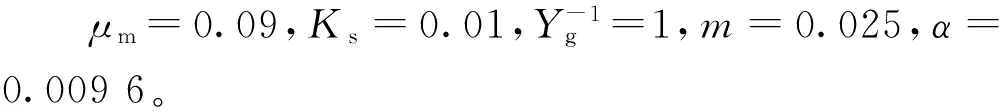
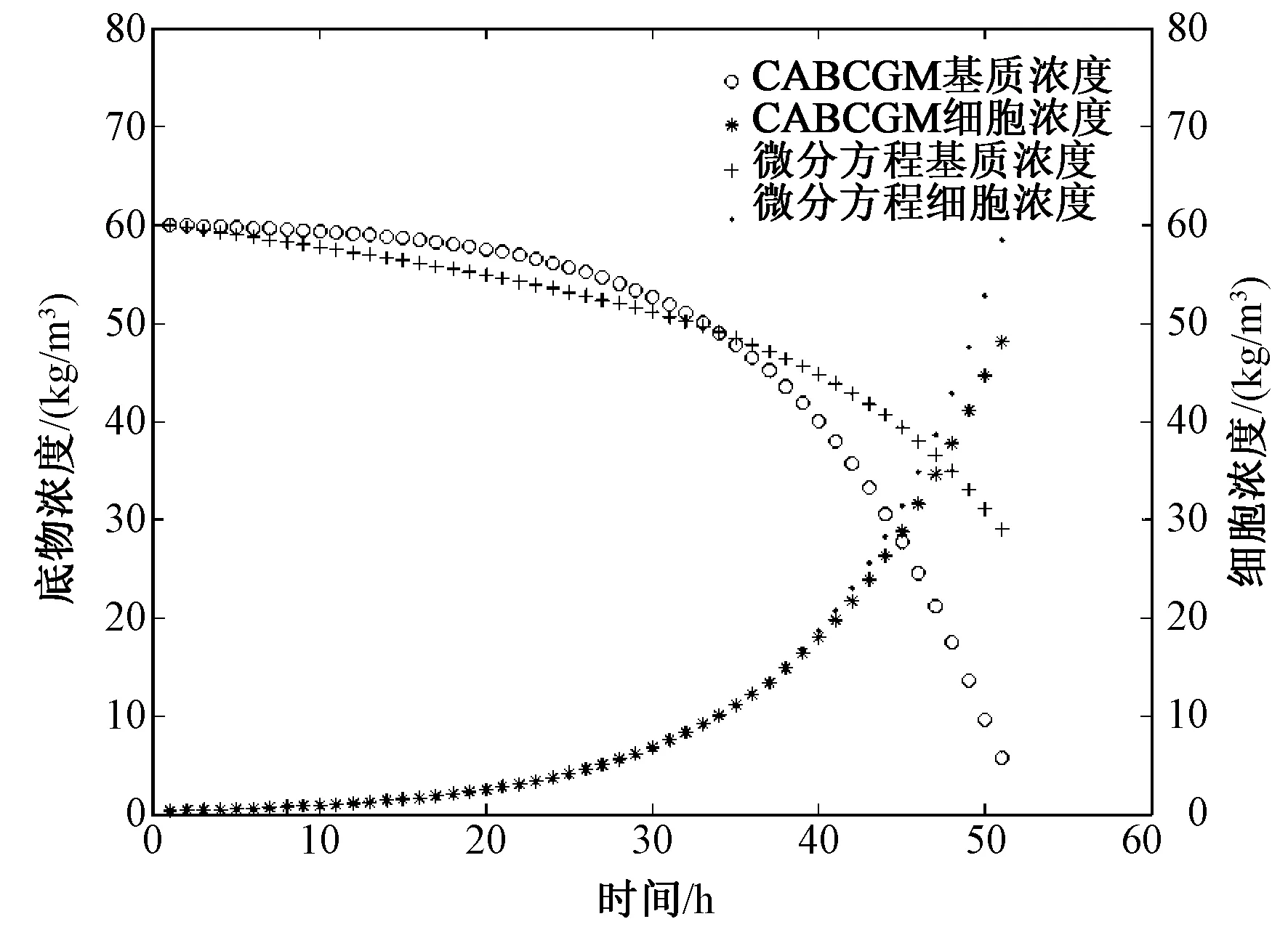
图1 CABCGM模型演化过程中细胞浓度随时间变化的曲线以及基质浓度随时间变化的曲线Fig.1 The cell concentration change over time in the evolution process of CABCGM model and the curve of the substrate concentration change over time

由图1可以看出，在开始的一段时间内，模拟的图像与微分方程描述的曲线比较吻合，说明设计的元胞自动机在规则和参数方面还较吻合，但随着时间的进行，图像出现较大的分离，尤其是基质消耗的曲线，说明当细胞增至一定数量后，基质瞬间被大量消耗，之前设计的元胞自动机的规则和参数不再适应。所以确切说，短期模拟细胞的生长，元胞自动机较微分方程表现出诸多的优势，但细胞数量到达一定值后，还需要调整元胞自动机参数等，而微分方程就不需要调整。

3 讨论和结论

本研究立足于生物细胞的生长机理，在莫诺德方程的基础上，推导出描述生物细胞生长的非线性动力学微分方程，通过考虑实际，对此微分方程设计参数，建立了模拟生物细胞生长演化的元胞自动机模型(CABCGM)，通过对元胞自动机进行规则的设计，该模型的仿真结果能较好地复现动力学微分方程所描述的生物细胞的生长演化过程，且更能表现出复杂系统的复杂性(多样性、随机性、鲁棒性、不确定性等)。本实验的新颖之处是：在莫诺德基础上，推导出了细胞的生长曲线微分方程，这与其他同行利用现成的微分方程离散化后再模拟是不同的。此外，本次模拟讨论点在基质瞬间被大量消耗的细胞值，确定了这个点后，可以让元胞自动机的模拟过程分段进行，该点之前的按照以前的规则和参数运行，该点之后的根据实际设计的新规则及参数进行。本课题的下一个研究重点是：利用CA模型的优点，更具体、更深入地模拟生物细胞的生长演变，如具体到细胞的各个周期、细胞的成熟、成熟后的分裂分化等。

[1] Bajpai RK, Reu BM. Evalution of feeding strategies in carbon-regulated secondary metabolite production through mathematical modeling. Biotechnology and Bioengineering. 1981, 23(4): 717-738.

[2] Menezes J. Mathematical modeling of penicillin-G fed-batch fermentation[J]. Journal of Chemical Technology and Biotechnology.1994,61(2):123-138.

[3] 李广运,韩力群. 人工生命及其基本原理[J]. 计算机仿真,2004(5):121-125.

[4] 喻海飞,汪定伟. 人工生命研究综述[J]. 信息与控制,2004(4):434-439.

[5] 卢欣华,孙吉贵,韩霄松,等. 人工生命：计算机与生物学交叉的前沿学科[J]. 计算机科学,2008(5):9-13.

[6] 黄文高,潘志庚. 人工生命在计算机图形学中的应用[J]. 计算机辅助设计与图形学学报,2005(7):1383-1388.

[7] 张晓荣. 计算主义:从Cyborg走向人工生命[J]. 青海社会科学,2007(1):133-135.

[8] Ray TS. An evolutionary approach to synthetic biology: Zen and the art of creating life. Artificial Life Journal, 1994,1(1/2):179-209.

[9] 于乃功,阮晓钢. 模拟青霉素发酵过程中菌体生长动态的细胞自动机模型[J]. 生物物理学报,2004(2):155-162.

[10] 于乃功,阮晓钢. 细胞自动机及其在菌体生长建模仿真中的应用[J]. 系统仿真学报,2004(12):2651-2654.

[11] 孔维宝,董妙音,李万武,等. 从莫诺方程谈起——生物类本科专业教学中3个相似方程的探讨[J]. 微生物学通报,2015(8):1599-1602.

[12] 郑学翔. 第二讲微生物生长动力学[J]. 酿酒科技,1982(4):22-27.

[13] 吴佩琮. 第四讲微生物生长代谢过程数学模型的建立[J]. 食品与发酵工业,1982(4):73-81.