基于熵权的磁流变减振器馈能结构方案分析

叶万权,杨礼康,岳 旭,孙海杰

(1.浙江科技学院 机械与汽车工程学院,杭州 310023;2.浙江工业大学 机械工程学院,杭州 310014)

基于熵权的磁流变减振器馈能结构方案分析

叶万权1,杨礼康1,岳 旭2,孙海杰1

(1.浙江科技学院 机械与汽车工程学院,杭州 310023;2.浙江工业大学 机械工程学院,杭州 310014)

为了合理评判磁流变减振器馈能结构方案的优劣性,结合减振器产品性能分析特点,采用模糊综合评价及熵值法构建磁流变减振器馈能结构评判体系。在确定各指标权重的基础上建立适合磁流变减振器馈能结构评价的计算方法,并在建立3种可行方案的同时通过计算得出各方案的评价分数,从而证明出直线电机式馈能结构为最可行方案。

模糊综合评价;熵值法;磁流变减振器;馈能结构

馈能型磁流变减振器是以磁流变液为阻尼液进而开发的一种新型智能减振器[1-3],具有较高的应用价值和良好的发展前景[4-6]。但是,目前基于磁流变减振器馈能结构的设计还处于初级阶段,国内外学者针对其馈能性能而制订的评价标准多样且繁杂,无法对其性能进行准确评判,而且由于各类馈能机构的工作机理存在较大差异,对它的具体结构性能更无法作出定性评价,也就无法准确地给出该减振器馈能结构的性能定位[7-10]。熵值法是工程方案选型中较为常见的评价方法,针对以上问题,笔者提出基于熵值法的磁流变减振器馈能结构方案评价方法,可对此类磁流变减振器馈能结构的性能做出有效的比较和判断。

1 馈能结构组合方案

本研究针对汽车悬架馈能型磁流变减振器结构方案进行评价分析,该结构可以大致分成发电、阻尼、运动转换和整流滤波4个子功能部分。其中,整流滤波功能由全桥整流滤波电路实现;阻尼功能则由磁流变减振器实现;其余2项系统功能则采用下述方法进行求解。馈能结构的形态学矩阵见表1,由表1可得多个组合方案。

表1 馈能结构的形态学矩阵Table 1 Morphological matrix of energy-regenerative structure

由于凸轮机构的几何尺寸较大,要安装在汽车悬架上比较困难,并且可靠性较差,能量回收效率不高,因此,根据车身实际条件并通过比较分析,选取合适的功能部件组成方案1(A1+B2)、方案2(A1+B3)、方案3(A2+B1)3个方案。

分析以上3个组合方案可知,方案1、方案2的馈能装置均为旋转发电机,但两者的运动传动机构不同,方案1采用齿轮齿条机构,故简称齿轮齿条式,方案2采用滚珠丝杆,故简称滚珠丝杆式。方案3的馈能装置为直线发电机,其中直线发电机的动子与磁流变减振器的活塞杆是通过联轴器直接连接的,故方案3简称直线电机式。

2 建立模糊评价的数学模型

2.1 制订评价指标

针对磁流变减振器的馈能结构,其评价体系主要依据评价目的、系统特点而制订。因此,在制订评价指标时要选出对性能影响较大的因素。

设馈能装置方案的评价指标集为U={u1,u2,…,ui,…,um},对于因素ui而言,设rij=R(ui,vj)表示馈能结构方案的隶属度,0≤rij≤1。论域U上的因素模糊子集为:

(1)

式(1)中:ai为对A的隶属度。

论域U上的等级模糊子集为:

(2)

式(2)中，bj为等级vj对应模糊子集B的隶属度,从而有关系式:

(3)

2.2 确定评价指标的权重

由于各指标对馈能结构的评价有着不同程度的影响,为了能让评价过程具有一致的权衡,在此对其进行权重设置,此处采用熵值法来确定综合权重。假设共有m个待评价的方案,n个评价指标,则指标数据矩阵为X=[xij]m×n,其中xij≥0。具体操作步骤[11]如下:

1)将所有指标进行同等程度的分量化,获得对应项的指标值权重为:

(4)

2)计算第j项指标的熵值:

(5)

式(5)中一般取k=1/lnm。

3)各指标的差异性系数为:

gj=1-ej。

(6)

其中,指标越重则gj便越大。

4)设定比重系数为:

(7)

2.3 求解模型

采用模糊算法进行综合评价,通过2级指标的权重向量Ti与模糊综合评价矩阵Ri的模糊计算可获得1级评价指标对评价等级的隶属向量Ci[12-13]:

Ci=Ti∘Ri。

(8)

然后再进行2级模型综合评价计算,通过1级指标的权重向量T和由Ci组成的评价矩阵C得到总的评价向量Z:

Z=T∘C。

(9)

3 馈能结构的模糊综合评价

3.1 确定指标的分级与赋值

上述3种悬架馈能装置由于在结构、工作机理等方面存在差异,因此,在制订指标时要统一评价标准。为此制订了5种指标:可安装性u1,即该装置的安装是否方便,越是便于安装则评分越高;可靠性u2,即悬架系统抵抗路面振动冲击而不被破坏的能力,系统越稳定，则可靠性越高,评分也越高;可集成性u3,即馈能装置与磁流变减振器的适配关系,可集成化程度越高则评分越高;制造成本u4,即馈能装置满足馈能要求时所花费的资金,成本越低,评分越高;馈能效率u5,即馈能装置的馈能能力的大小,馈能潜力越大,评分越高。一般用评价集{很好,好,中等,一般,较差}来反映各项指标的大致情况[14]。利用式(1)～(2)确定指标的分级、赋值,具体见表2。

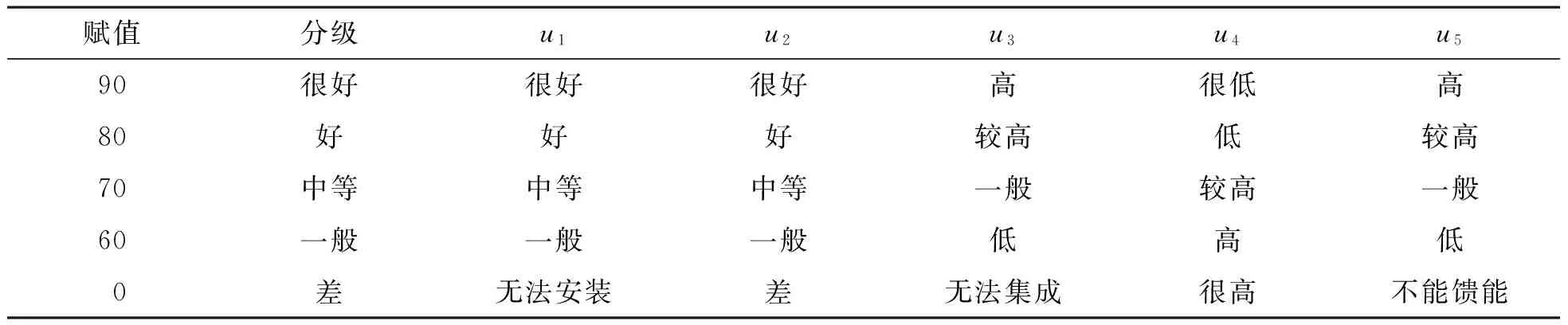
表2 各指标的分级及赋值表Table 2 Classification and assignment table of each index

根据磁流变减振器馈能结构的馈能特点可得出这3种馈能结构的评选指标模糊评语集,见表3。

表3 评选指标的模糊评语集Table 3 Fuzzy comment set of selection index

结合表2的分级赋值表和表3的模糊评语集,可获得各个方案的评判指标的分量化值,见表4。

表4 评选指标分量化表Table 4 Component table of selection index

3.2 确定各评价指标的权重及隶属度

由式(4)～(7)可以计算得出磁流变减振器馈能结构评价指标的权重,计算结果见表5。

表5 指标权重计算结果Table 5 Calculation results of index weight

由表5可知A=[0.130 3,0.341 2,0.163 5,0.104 2,0.260 8],因此,在设计馈能结构时应重视第2个和第5个评选指标,即馈能结构的可靠性和馈能效率,然后根据各隶属度(即权重系数)的大小依次考虑可集成性、制造成本和可安装性。

对于在取值区间(A,B)内的指标点,XB=1-(ui-A)/(B-A),XA=1-(B-ui)/(B-A),其他为0;而对于在区间(A,B)以外的指标点,离其最近端点的隶属度取值为1,其他都取0。根据上述方法得到评价矩阵为:

3.3 模型求解

根据馈能型的结构方案评价[15],然后由式(3)计算出模糊评价集对应各评价指标的隶属度函数B1、B2和B3。

B1=A·R1=[0.251 1,0.212 4,0.281 0,0.150 6,0],
B2=A·R2=[0.414 8,0.479 9,0.065 1,0,0],
B3=A·R3=[0.481 4,0.146 8,0.212 1,0.212 1,0]。

由公式Q=B·UT得到3种设计方案的评选结果分别为:64.872,77.443,89.123。从计算结果中可以看出,直线电机式馈能结构所得分数最高,虽然可能存在一定的模糊差异性,但已被证明是最可行的方案。

4 结 语

针对磁流变减振器不同的馈能结构,笔者提出了3种可行的结构方案。通过建立统一的评价指标,部分消除由于其结构和馈能机理的差异而产生的评价误差。采用模糊熵值法对3种结构进行论证,通过建立模型和赋值计算,说明直线电机式的馈能结构是最可行的馈能型悬架结构方案,它具有可靠性好、可集成化程度高和馈能效率高等优势。因此,模糊熵值法可以作为磁流变减振器馈能结构方案的有效评价方法,为今后减振器馈能结构的深入研究提供参考。

[1] ZHU S X, WANG P, TIAN J. Experimental research on aircraft landing gear drop test based on MRF damper[J].Procedia Engineering,2011,15:4712.

[2] KIM Y, LANGARI R, HURLEBAUS S. Semiactive nonlinear control of a building with a magnetorheological damper system[J].Mechanical Systems and Signal Processing,2009,23(2):300.

[3] TSAMPARDOUKAS G, STAMMERS C W, GUGLIELMINO E. Hybrid balance control of a magnetorheological truck suspension[J].Journal of Sound and Vibration,2008,317(3):514.

[4] 王戡.集成永磁直线发电机的汽车自供电磁流变减振器研究[D].重庆:重庆大学,2013.

[5] 董小闵,陈孝荣,丁飞耀.磁流变减振器自供能系统设计研究[J].机械设计与制造,2013,12(12):8.

[6] 战敏.液电式馈能减振器动力学仿真和性能研究[D].长春:吉林大学,2015.

[7] 黄国庆,王明绪,王国良.效能评估中的改进熵值法赋权研究[J].计算机工程与应用,2012,48(28):245.

[8] 郑志宏,魏明华.基于熵值法的改进集对分析水质模糊评价[J].河海大学学报(自然科学版),2013,41(2):136.

[9] 王化培,石晓辉.机械设计方法学[M].重庆:重庆大学出版社,1996.

[10] 廖昌荣,余淼,杨建春,等.汽车磁流变减振器设计中值得注意的若干技术问题[J].汽车技术,2001(5):11.

[11] 王美乂,张凤鸣,刘智.模糊信息的熵权多属性决策方案评估方法[J].系统工程与电子技术,2006(10):1523.

[12] 马开良,王志,张进生,等.基于熵权的建筑垃圾破碎站结构方案的模糊综合评价[J].机械设计,2015(9):76.

[13] HAN K M, LI F M, LI H Y. Fuzzy comprehensive evaluation for stability of strata over gob influenced by construction loads[J].Energy Procedia,2012,16:1102.

[14] 刘健,过学迅.基于模糊综合评价法的馈能悬架结构方案评价[J].交通科技与经济,2011,13(1):90.

[15] 何仁,陈士安,陆森林.馈能型悬架的工作原理与结构方案评价[J].农业机械学报,2006(5):5.

Scheme analysis of energy-regenerative structure of MR damper based on the entropy method

YE Wanquan1, YANG Likang1, YUE Xu2, SUN Haijie1
(1. School of Mechanical and Automotive Engineering, Zhejiang University of Science and Technology, Hangzhou 310023, Zhejiang, China; 2. College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, Zhejiang, China)

In order to reasonably evaluate the merits and demerits of the energy-regenerative structure schemes of MR damper, this article has adopted the fuzzy comprehensive evaluation and the entropy method to construct the evaluation system of the energy-regenerative structure of MR damper, in combination with analysis of the shock absorber performance. Meanwhile, the article has formulated the calculation method for evaluating the energy-regenerative structure of MR damper on the basis of determining the weight of each index. Finally, the article proves the linear motor energy-regenerative structure to be the most feasible scheme by calculating evaluation scores of three feasible schemes.

fuzzy comprehensive evaluation; entropy method; MR damper; energy-regenerative structure

10.3969/j.issn.1671-8798.2017.01.008

2016-12-24

国家自然科学基金面上项目(51175474);浙江省大学生创新创业孵化项目(2016R415004);浙江科技学院研究生科研创新基金项目(2016yjskc005)

杨礼康(1971— ),男,山西省闻喜人,教授，博士,硕士生导师,主要从事磁流变减振器方面的研究。E-mail:104019@zust.edu.cn。

U463.335.1

A

1671-8798(2017)01-0043-05