一种改进的人工蜂群算法优化的支持向量机

李纪麟 谢霖铨

摘 要：为了改善现有支持向量机（Support Vector Machine）的机器学习效果依赖于参数选择，而参数选择通常依赖于经验的问题，在现有基础上，本文结合一种称为骨架人工蜂群算法（Bare-bones Artificial Bee Colony）的改进的人工蜂群算法对支持向量机的2个参数进行优化，并对该优化结果进行试验。试验结果表明，改进的支持向量机的准确率、识别速度均优于原本的支持向量机。

关键词：支持向量机；人工蜂群算法；参数优化

中图分类号：TP18 文献标识码：A 文章编号：1003-5168（2017）03-0046-05

Abstract： In order to improve the performance of existing support vector machine in machine learning that depends on the parameters of SVM， and the parameters always depend on the experience of the problem， based on the existing conclusion， an SVM that hybrid with an improved artificial bee colony algorithm called bare-bones artificial bee colony algorithm was proposed to optimize the two parameters of SVM， and the optimized results were tested. The results showed that the improved SVM had better accuracy and recognition speed than the original support vector machine.

Keywords： support vector machine；artificial bee colony algorithm；parameter optimizing

支持向量机（Support Vector Machine，SVM）是一种监督式的机器学习方法，能非常成功地处理回归问题（时间序列分析问题）和分类问题等诸多问题，并可推广用于预测和综合评价等领域[1]。支持向量机经过多年的发展，已经出现了多种改进算法，使得其性能有了很大的改进[2]。文献[3-5]通过实验证实核函数的参数的正确选择对于SVM的性能有着至关重要的影响。现在通常使用的核函数是RBF核函数[4-8]。SVM的参数选择实际上是一个优化问题。截至目前，SVM的参数选择包括如下方法：经验选择法、交叉验证法、网格搜索法、贝叶斯法等[7]。近年来，随着包括模拟退火算法（Simulate Annealing Algorithm，SA）[9]、遗传算法（Genetic Algorithm，GA）[10]、粒子群优化算法（Particle Swarm Optimization Algorithm，PSO）[11]和人工蜂群算法（Artificial Bee Colony Algorithm，ABC）[12]等优化算法的发展，已有学者采用上述算法来优化选择SVM的参数[4，7，13]。

骨架人工蜂群算法（Bare-bones Artificial Bee Colony，BBABC）是一种改进的人工蜂群算法[14]。该种算法相比原始的ABC及其他的优化算法，有更好的收敛精度和收敛速度。本文使用BBABC对使用径向基函数（Radial Basis Function，RBF）作为核函数的SVM的2个参数进行优化，并对优化的结果进行试验，取得了较好的效果。

1 人工蜂群算法

人工蜂群算法是一种启发式群体智能优化算法。该算法的基本思想是通过模拟蜂群中个体之间的分工和信息交流，相互协作寻找蜜源的过程。与经典的优化方法相比，ABC算法对目标函数和约束几乎没有要求，在搜索过程中基本不利用外部信息，仅以适应度函数作为进化的依据，即是使用“生成+检验”的方式[12]，這种方式十分适合用于解决NP完全问题。ABC算法具有操作简单、控制参数少、搜索精度较高和鲁棒性较强的特点[15-17]。Karaboga等[16]指出与遗传算法、差分演化算法（Differential Evolution，DE）和粒子群优化算法相比较，ABC算法的求解质量相对较好。

Bare-Bones人工蜂群算法（BBABC，又称BABC或BCABC）[14]是一种新型的基于ABC的改进算法。该算法针对原始ABC具有较强的搜索性能和较弱的收敛性，引入了移动距离参数自适应，基于适应度的最近邻，以及在跟随蜂阶段引入高斯搜寻方程这三种方式来提高算法的收敛性。通过结合这三种方式，该算法能够极大地提升ABC的收敛性，从而提升ABC的性能。

1.1 人工蜂群算法的基本原理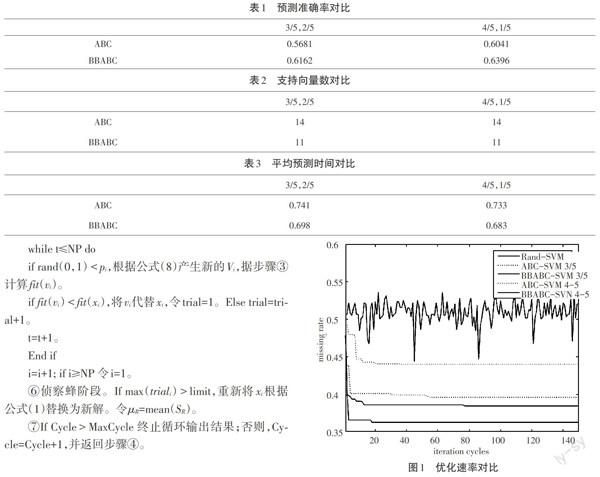

1.1.1 群体智能模型的组成。对于一个给定的优化问题，ABC算法使用一个模拟蜂群寻找更好的食物源的群体智能模型来寻找该优化问题的解。这个群体智能模型由3种类型的蜜蜂及食物源组成。具体的定义如下。

1.1.1.1 食物源。ABC算法中的食物源是连续或离散的解空间中的点。对于每一个点i，定义一个函数fit（xi）作为评价该点处蜜源的标准，这个标准也称为适应值。

ABC算法把蜂群分为2个部分，2种蜜蜂分别使用不同的策略来寻找新的食物源。将蜂群划分的方式通常是50%为雇佣蜂，50%为跟随蜂。

1.1.1.2 雇佣蜂（Employed Bees）。蜂群的两种分类的其中一种是雇佣蜂。雇佣蜂寻找新的食物源的方式是在现有食物源的基础上进行开采，在这个过程中可能雇佣跟随蜂或不雇佣；雇佣跟随蜂的过程即是“雇佣蜂”这个名字的由来。

1.1.1.3 跟随蜂（Onlooker Bees）。蜂群的另一个部分是跟随蜂。顾名思义，跟随蜂的任务是选择一个雇佣蜂并和该雇佣蜂一起对雇佣蜂所处的蜜源进行开发。

1.1.1.4 侦察蜂（Scout Bees）。雇佣蜂在认为一个蜜源没有继续开采的价值时（通常认为该蜜源已陷入局部最优的情况），他就会转变为侦察蜂并在全局搜索一个新的蜜源。侦察蜂在选择了一个新的蜜源之后将会重新转变为雇佣蜂。

1.1.2 ABC算法的过程。对于一个解空间的维度为D的问题，ABC算法的过程如下。

如上所述，使用RBF作为核函数的支持向量机具有2个参数：惩罚因子C和RBF参数σ。王鹏等[4，5]实验论证了这两个参数的正确选择对SVM的准确性具有重要影响。

3 通过BBABC进行参数选择的支持向量机

如上文所述，支持向量机的参数选择对其计算的准确性和泛化能力有重要影响。截至目前，支持向量机的参数选择法主要包含：经验选择法、交叉验证法、网格搜索法、贝叶斯法以及包括SA、GA、PSO、ABC等优化算法。其中，经验选择法依赖于问题描述和使用者的经验，依赖于问题本身；交叉验证法、网格搜索法等算法较为盲目，时间复杂度较高，收敛性较差。现有的优化算法虽然具有一定的收敛性，但仍然稍显不足。

通过使用支持向量机的分类准确率作为基础计算适应度，则准确率越高，适应度越小。因此可以据此将BBABC和SVM相结合，算法步骤如下。

①预处理数据集，将数据集分为训练集A和测试集B。Cycle=1。

4 试验分析

4.1 数据来源

试验使用加州大学欧文分校（University of CaliforniaIrvine）提供的UCI数据集其中之一的Wine Quality数据集。该数据集包含产自北葡萄牙的葡萄牙青酒随机取样的4 898个样本，每个样本包含通過物理化学方式测量的密度、pH值、酒精度等12项特征。最终的质量评级包含10个等级[19]。试验前已将所有特征归一至[0，1]区间。试验分为2次，一次以前3/5的数据作为训练集，后2/5的数据作为测试集。另一次以前4/5的数据作为训练集，后1/5的数据作为测试集。

ABC的参数作如下设置：种群数为50，引领蜂数量为25，最大搜索次数设置为30， 最大迭代次数为150。

4.2 对比和评价标准

4.3 结果与分析

4.3.1 优化速率和识别准确率对比。使用随机数、ABC、BBABC算法对SVM参数进行优化，优化速率见图1。使用优化所得的参数建立识别模型，识别准确率见表1，支持向量数见表2。结果表明，使用BBABC的算法效率、支持向量数及识别准确率均优于ABC算法。

相对于原始ABC SVM，BBABC-SVM的平均预测时间较少，识别速度较快。这主要由于BBABC-SVM减少了支持向量的数量，加快了算法的收敛速度。

4.3.2 识别时间对比。在实际运用中，许多应用需要保证实时性，因而预测速度也十分重要。为此，对上述数据的平均预测时间（单位s）进行仿真试验，结果如表3所示。

5 结语

由上述优化效果可见，使用BBABC优化的SVM因为利用了BBABC的自适应机制向最优解方向收敛，在时间上和识别准确率上均优于使用ABC优化的SVM，但识别准确率仍稍显不足。这可能是由于两方面的原因：一是由于支持向量机的优化是一个多峰值的问题，算法可能由于早熟收敛陷入了局部最优；二是分类样本各类的分布不均匀。接下来的研究将围绕避免早熟收敛、使算法跳出局部最优的方向展开。

参考文献：

[1]VN Vapnik. The Nature of Statistical Learning Theory[M].New York：John Wiley and Sons，1998.

[2]丁世飞，齐丙娟，谭红艳.支持向量机理论与算法研究[J].电子科技大学学报，2011（1）：2-10.

[3]陈健飞，蒋刚，杨剑锋.改进ABC-SVM的参数优化及应用[J].机械设计与制造，2016（1）：24-28.

[4]王鹏，郭朝勇，刘红宁.基于支持向量机的枪弹外观缺陷识别与分类[J].计算机工程与科学，2016（9）：1943-1949.

[5]M Zuriani，Y Yuhanis，SK Siti. Enhanced artificial bee colony for training least squares support vector machines in commodity price forecasting[J].Journal of Computational Science，2014（5）：196-205.

[6]张博洋.支持向量机理论与应用研究综述[J].无线互联科技，2015（19）：111-112.

[7]宁爱平，张雪英，刘俊芳.ABC-PSO算法优化混合核SVM参数及应用[J].数学的实践与认识，2014（18）：158-165.

[8]古丽娜孜·艾力木江，孙铁利，乎西旦.一种基于融合核函数支持向量机的遥感图像分类[J].东北师大学报（自然科学版），2016（3）：60-66.

[9]AG Khachaturyan，SV Semenovskaya，BK Vainshtein. Statistical-Thermodynamic Approach to Determination of Structure Amplitude Phases[J].Sov. Phys. Crystallography，1979（5）：519-524.

[10]AE Eiben，PE Raué，Z Ruttkay. Genetic algorithms with multi-parent recombination[A]//International Conference on Evolutionary Computation，1994：78-87.

[11]KennedyJ，Eberhart R. Particle Swarm Optimization[A]//IEEE International Conference on Neural Networks，1995：1942-1948.

[12]Dervis Karaboga. An Idea Based On Honey Bee Swarm for Numerical Optimization[D].Erciyes：Erciyes University，2005.

[13]蔡丽霞，马琰.基于ABC-SVM的考生行为自动识别[J].計算机系统应用，2015（5）：129-134.

[14]W Gao，FTS Chan，L Huang，et al. Bare bones artificial bee colony algorithm with parameter adaptation and fitness-based neighborhood[J].Information Sciences，2015（C）：180-200.

[15]D Karaboga，B Akay. A comparative study of artificial bee colony algorithm[J].Applied Mathematics and Computation，2009（14）：108-132.

[16]D Karaboga，B Basturk. On the performance of artificial bee colony（ABC）algorithm[J].Applied Soft Computing，2008（1）：687-697.

[17]秦全德，程适，李丽，等.人工蜂群算法研究综述[J].智能系统学报，2014（2）：127-135.

[18]王慧颖，王文彬.基于改进搜索策略的混合蜂群算法[J].系统工程与电子技术，2014（10）：2094-2101.

[19]P Cortez，A Cerdeira，F Almeida，et al. Modeling wine preferences by data mining from physicochemical properties[J]. Decision Support Systems，2009（4）：547-553.