振动电机非线性气隙偏心机理研究

孟东容，段志善，郭宝良，张 健，刘佳敏

(西安建筑科技大学，西安 710055)

0 引 言

振动电机广泛应用于采矿、选矿、煤炭、冶金、石油等各个领域[1]。由于工作环境较差，振动电机出现故障的频率较高，要对其进行故障诊断,首先要对振动电机的正常工作状态进行研究。因此振动电机正常工作状态分析的研究具有重要的理论价值和实际应用意义。

电机电感参数受气隙长度的影响，振动电机结构特殊，它工作时所形成的气隙与普通电机的气隙并不相同。现阶段国内外对电机气隙偏心的研究主要集中在静态、动态或混合偏心上，Thomson[2-5]等人针对静偏心下的三相电机采用有限元法和快速傅里叶分析预测了电流中的特定频率分量幅值；Faiz[6]等学者用有限元方法对混合偏心状态下感应电机的性能进行了分析；Akiyama[7]等基于实际情况提出了斜偏心模型，分析了气隙偏心度与转子倾斜角和轴向位置的关系。但是，这些偏心类型的转子都是线性的，鲍晓华[8]提出在实际电机的偏心中还有一类动态弧偏心模型，但没有对这种故障进行深入分析。

本文对振动电机特有的非线性动态弧偏心的形成机理进行了详细分析，推导了弧偏心模型下气隙长度的计算公式，计算了振动电机定子绕组中形成的特定频率的电流分量，通过仿真验证了计算结果的准确性。并通过对不同轴向位置特定频率幅值的分析,证明了振动电机转子主轴受力弯曲程度与定子绕组电流特定频率幅值具有正比例关系。

1 振动电机的结构

1.1 振动电机与普通电机结构上的区别

振动电机从结构上来说就是在转子主轴的两端装有偏心块的电动机。根据电机伸出轴个数的不同，振动电机分为单出轴振动电机和双出轴振动电机两种。单出轴振动电机的转子主轴只在一端伸出并装有偏心块,双出轴振动电机转子主轴两端均伸出并装有偏心块。

本文以双出轴振动电机为对象进行分析，其转子与普通电机相比,直径略大,长度略短,气隙长度略大,其工作原理与普通电机基本相同。振动电机结构简图如图1所示。

图1 振动电机结构简图

1.2 振动电机转子受力分析

由于振动电机结构上的特殊性，导致其转子主轴在工作时会产生不同于普通电机转子主轴的形变。在普通异步电机转子旋转时作用在转轴上的力主要有：电机产生的扭矩、转子的惯性力和轴承的支反力。对于振动电机而言，其转子旋转时作用的力除了普通电机转子受到的力，还有偏心块产生的离心力和偏心块的惯性力。相比较而言，离心力的值远大于转子上所受其他力的值，因此在对转子进行受力分析时,可忽略其他力的作用。根据材料力学基本知识，转子可近似为简支梁来计算其受力和形变，如图2所示。

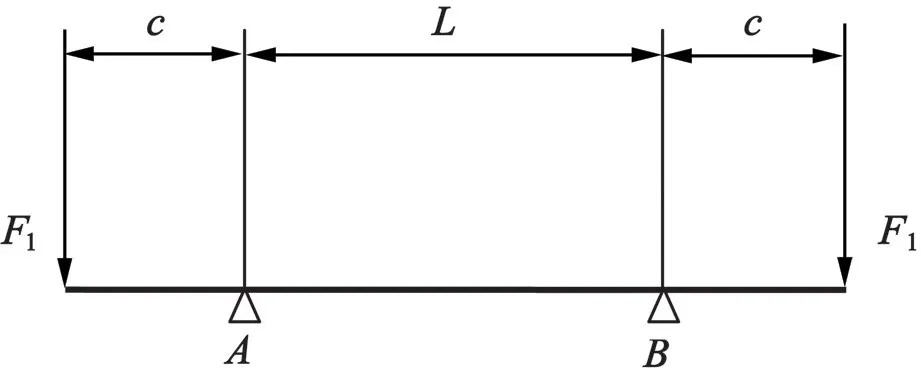
图2 转子主轴受力简图

将转子主轴简化为简支梁来计算其形变方程，设离心力为F1：

F1=mγω2

(1)

式中：m为单个偏心块的质量；γ为偏心距，见图1；ω为偏心块转动角速度。

轴承A，B处的支反力：

FA=FB=F1

(2)

计算AB之间的挠曲线方程,建立如图3所示的坐标系。

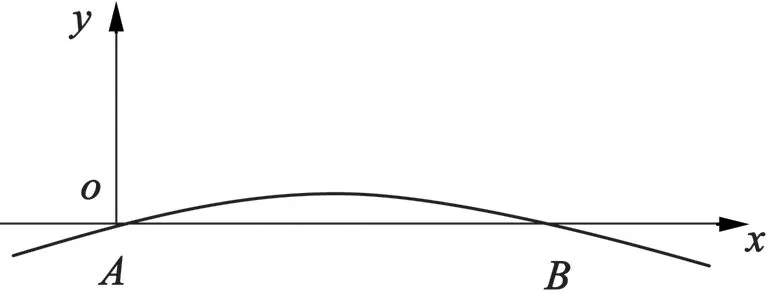
图3 电机主轴变形图

弯矩：

M=F1x

(3)

根据材料力学中计算挠曲线方程的方法，两次积分后得到转子主轴的挠曲线方程如下：

(4)

代入A,B两点的坐标后可计算得C1和D1两个常数的值，从而得到AB段的挠曲线方程：

(5)

2 振动电机弧偏心模型的建立

由上述结果可知，振动电机运行时，转子主轴根据激振力的大小产生不同程度的变形,其不同轴向位移的变形程度不同,因此转轴与定子间的气隙是时刻变化并且与轴向的位置有关。

2.1 普通电机的气隙偏心

电机的气隙偏心有静态偏心与动态偏心两种基本情况[9]，如图4所示。偏心即电机的定子轴心与转子轴心不重合，静态偏心是指气隙的偏心位置不随着转子的旋转而改变，是固定在某一位置的。

(a) 静偏心

(b) 动偏心

动态偏心是指偏心的位置对转子是固定的，对定子是不固定的。

转子的气隙偏心会导致电机的气隙磁导发生变化，进而影响电机的电感和气隙磁通密度，最终会在定子电流中产生特征频率。S.Nandi[10]等人给出了电机气隙复合偏心时的气隙长度计算公式：

δ(φ,t)=δ0[1-kscosφ-kdcos(ωrt-φ)]

(6)

式中：δ0为平均气隙长度；ks为静态偏心度；kd为动态偏心度；ωr为转子旋转角频率；φ为定子坐标系的圆周角位移。

2.2 振动电机气隙长度的计算

振动电机的偏心不同于上述单纯的静态或动态偏心，因为其气隙长度不仅随时间和角位移变化，而且随着轴向的位移而不同。由上述计算可知，振动电机运行时，由于激振力会使转子主轴产生弯曲变形，这种变形会让振动电机的定、转子之间形成一种特殊的偏心，如图5所示。

图5 振动电机的弧偏心

从图5中可以看出，振动电机在激振力不为零时，转子主轴的变形会导致其产生特殊的弧偏心，在目前的电机偏心故障研究中均假设转子是线性的，但振动电机的转子由理论计算结果可知，它是非线性的。

因为双出轴振动电机的弧偏心状态在工作时其最小气隙位置是随时间变化的，这与动态偏心的机理一致，在不考虑电机制造、装配过程中造成的偏心并忽略静态偏心存在的情况下，振动电机正常时，令式(6)中的ks为0,可得振动电机的气隙长度：

δ(φ,t,x)=δ0[1-kd(x)cos(ωrt-φ)]

(7)

式中：kd(x)为振动电机弧偏心的偏心率。根据计算得出的转子的挠曲线方程，计算得弧偏心的偏心率：

(8)

式中：x是电机轴向的位移。可以看出，弧偏心的偏心率是在x轴上随着位移而变化的。

2.3 弧偏心特征的机理分析

电机的弧偏心是由于双出轴振动电机运行时转子主轴两端受到很大的激振力而导致的，由于电机的气隙偏心会导致气隙磁导的变化，因此，下文计算了在弧偏心时，某一时刻转子主轴任意位置的气隙长度的倒数和气隙磁导，并通过电磁感应基本原理计算了电机定子电流中会出现的特征频率。

气隙长度的倒数：

(9)

当忽略电机定转子开槽及饱和的影响时,将气隙长度倒数简化，经傅里叶展开后仅取一次项得：

(10)

式中：λ为气隙磁导，λ=μ0/δ(φ，t，x)，μ0为真空磁导率。

假设定、转子绕组正常，三相绕组基波磁势的一次谐波可表示：

J(φ,t)=Jscos(ωt-pφ)

(11)

式中：Js为定子线负荷的幅值；p为极对数。

根据基本磁路理论，磁感应强度等于磁势与气隙磁导的乘积，即：

B(φ,t)=J(φ,t)λ(φ,t,x)

(12)

定子气隙磁场表达式：

(13)

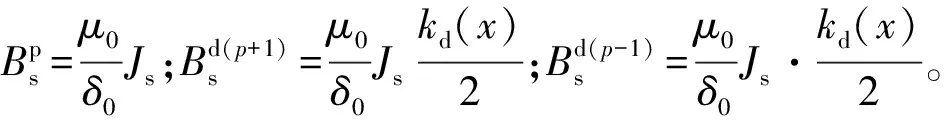
(14)

因为ωr=(1-s)ω/p，其中s为转差率，代入式(14)中得定子1次谐波磁势建立的磁场所产生的磁链和交链各转子回路的磁链，从而在求导之后能够得到转子回路对应的感应电势。该频率的电势产生的转子电流可以产生转子磁势，可表示：

(15)

式中：β1，β2，β3均为相位角。将上式变换到定子坐标系中，可得：

(16)

式中：γ1，γ2，γ3均为相位角。将式(16)与气隙磁导相乘，得到转子感生电流所建立的气隙磁场：

由于气隙的弧偏心，定子绕组中会感生电势，并产生电流，对任一相定子电流进行频谱分析将会有边频带出现，而只有极对数为p的分量才能在定子绕组中感应出有效电势，其中ω对应f1，ωr对应fr。因此，对上式分析可以得出，定子绕组的频谱图中会感应出频率为f1±fr的特征频率。

3 振动电机数学模型及仿真

3.1 交流电机的多回路理论

为研究交流电机绕组不对称状态，我国学者高景德、王祥珩[11]提出了多回路理论分析方法，建立了电动机和发动机内部故障的数学模型。

假设，在一个感应电机中有m个定子回路和n条转子导条。感应电机的数学模型可以用下面的公式来表述[11]：

定子电压方程：

(18)

式中：U为电压矩阵；ψ为磁链矩阵；I为电流矩阵；R为电阻矩阵；下标“s”，“r”分别表示定子和转子。

转子电压方程：

(19)

定子磁链方程：

ψs=LssIs+LsrIr

(20)

式中：Lss为定子自感矩阵；Lsr为定、转子互感矩阵。

转子磁链方程：

ψr=LrsIs+LrrIr

(21)

式中：Lrr为转子自感矩阵；Lrs为转、定子互感矩阵。且：

(22)

感应电机的转矩方程如下：

(23)

(24)

式中：θ为转子角位置；ω为转子机械角速度；Te为电磁转矩；TL为负载转矩；J为转子的转动惯量。

Te可以通过下式计算：

(25)

式中：

(26)

联立以上各式，采用Runge-Kutta方法可以求解该微分方程组，从而得到定子电流。

3.2 振动电机电感参数的计算

交流电机电感参数的计算公式如下[12-13]：定子绕组的自感系数：

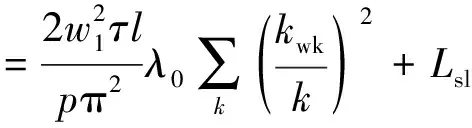
(27)

定子绕组间的互感系数：

MAB=MBC=MCA=MBA=MCB=MAC=

(28)

式中：w1为每相定子绕组串联的匝数；τ为极距；λ0为气隙磁导，δ是有效气隙长度；kwk为定子绕组系数；l为定子铁心长度；Lsl和Msl分别是定子绕组的漏磁自感系数和漏磁互感系数，k=1,3,5,…。

转子回路的自感系数：

(29)

式中：i代表n+1个转子回路的序号;Lb,Le分别为转子导条电感和转子端环电感。

两个转子回路之间的互感系数：

(30)

转子端环与转子回路的互感系数：

Mei=Mie=Le

(31)

定子绕组与转子回路间的互感系数：

(32)

式中：k=1,3,5,…；s代表A,B,C三相;βr代表短距比;φ=2pπ/n是电角度。

在式(32)中λ0为常数，前面已经得出振动电机的气隙长度并不是固定值，而是随着轴向位移变化的，即：

δ(φ,t,x)=δ0[1-kd(x)cos(ωrt-φ)]

(33)

因此，在振动电机中，电感参数是随轴向的位移而变化的，将电感参数在定子长度l上进行微分得：

(34)

再对其在定子铁心长度l上进行积分，可得：

(35)

用相同方法进行积分可得如下公式。

定子间互感系数：

MAB=MBC=MCA=MBA=MCB=MAC=

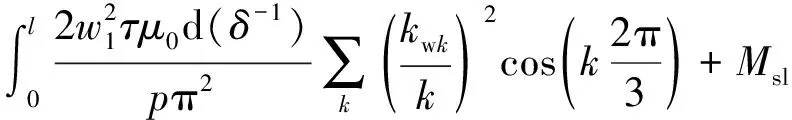
(36)

转子回路的自感系数：

(37)

转子两回路之间的互感系数：

(38)

定子绕组与转子回路间的互感系数：

(39)

根据上述公式可计算出振动电机中的各电感参数，代入多回路模型中即可得出电机的定子相电流。

3.3 基于多回路理论的振动电机仿真

根据交流电机多回路理论，结合上述电感参数的计算方法，利用MATLAB/Simulink对振动电机进行仿真，输出定子A,B,C三相电流，并对A相电流进行FFT分析，得到结果如图6、图7所示。其中，横坐标为频率，纵坐标为特征频率与基频的比例关系。

图6 三相异步交流电机A相电流频谱图

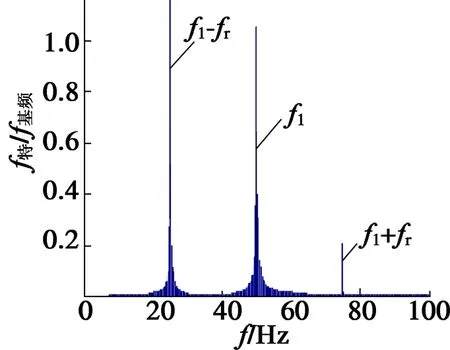
图7 振动电机A相电流频谱图

上述仿真中设定电机转速为1 500 r/min,根据理论分析可知，在振动电机A相电流频谱图中将会出现f1±fr的特征频率，而1 500 r/min的转子频率为25 Hz，由对比可以看出，在振动电机的基频50 Hz左右分别出现25 Hz和75 Hz的特征频率，这与理论分析结果一致。

振动电机激振力的大小决定了转子的挠曲线方程，在不同轴向位移处会得到幅值大小不同的特征频率。对此，在振动电机两支点间主轴上取20个样本点，分别计算其电感参数，得到对应的频率幅值。假设转子转速1 500 r/min，计算25 Hz特征频率的幅值，以轴向样本点序号为横坐标，不同位移处特征频率的幅值与最大位移处的幅值的比值为纵坐标，绘制图形如图8所示。

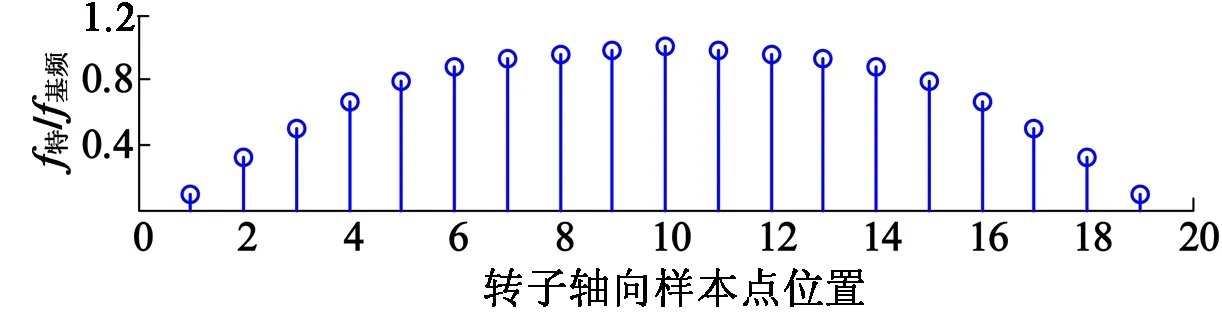
图8 不同轴位移处特征频率幅值比

图8表明,由于轴向位置的不同,电机偏心程度不同,以上述20个样本点为例,这20个点所对应的特征频率幅值与最大幅值比组成的图形能够反映出电机转子的形变状态。将这20个样本点幅值比相连，就可以得到挠曲线方程y(x)的近似图形。这表明振动电机特定频率的幅值与振动电机转子主轴弯曲程度成一定的正比例关系。

4 结 语

1)振动电机受到偏心块激振力的作用会产生形变，通过计算得到振动电机转子弯曲的曲线方程。

2)振动电机与普通电机正常运行时具有差异性。理论分析表明，振动电机正常运行时在定子电流中会感应出特征频率f1±fr。

3)通过转子主轴的形变方程，结合混合气隙长度的计算公式，提出振动电机弧偏心的气隙长度计算公式。

4)基于多回路理论，建立了振动电机的数学模型，利用MATLAB进行仿真，证明了理论分析的准确性。并提出了振动电机转子主轴弯曲程度与振动电机定子电流特征频率幅值的正比关系，可以有效减少振动电机故障诊断的误判断。

[1] 庄表中.(一)振动电机[J].振动与冲击,1992,(Z1):132.

[2] THOMSON W T，BARBOUR A.On-line current monitoring and application of a finite element method to predict the level of static air gap eccentricity in three-phase induction motors[J]． IEEE Transactions on Energy Conversion，1998，13(4)：347-357．

[3] WU Long，LU Bin，HAUNG Xianghui.Improved online condition monitoring using static eccentricity-induced negative sequence current information in induction machines[C] // IECON 2005: 31st Annual Conference of IEEE Industrial Electronics Society， 2005：1737-1742.

[4] SUPANGAT R,GRIEGER J,ERTUGRUL N.Investigation of static eccentricity fault frequencies using multiple sensor in induction motors and effects of loading [C]// IECON 2006 - 32nd Annual Conference on IEEE Industrial Electronics，2006：958-963.

[5] GRIEGER J，SUPANGAT R，ERTUGRUL N.Induction motor static eccentricity severity estimation using evidence theory [C]// IEEE International Electric Machines and Drives Conference, IEMDC 2007，2007：190-195.

[6] FAIZ J，EBRAHIM B M，AKIN B.Finite-element transient analysis of induction motors under mixed eccentricity fault [J].IEEE Transactions on Magnetics，2008，44(01)：66-74.

[7] AKIYAMA Y.Unbalanced-heating phenomenon of induction motor with eccentric rotor [J].Industry Applications Society Meeting, 1992(1):107-114.

[8] 鲍晓华,吕强.感应电机气隙偏心故障研究综述及展望[J].中国电机工程学报,2013,33(6):93-100.

[9] 沈标正．电机故障诊断技术[M].北京：机械工业出版社,1996.

[10] 汤蕴璆，史乃.电机学[M].北京：机械工业出版社，2001.

[11] NANDI S,BHARADWAJ R M,TOLIYAT H A.Mixed eccentricity in three phase induction machines: Analysis, simulation and experiments[C]//Conference Record - IAS Annual Meeting (IEEE Industry Applications Society)，2002：1525-1532.

[12] 高景德，王祥珩．交流电机的多回路理论[J]．清华大学学报(自然科学版)，1987，27(1)：1-8.

[13] 高景德，王祥珩，李发海．交流电机及其系统的分析[M]．北京：清华大学出版社，1993.