对“未来偶然命题”的逻辑思考

一、什么是“未来偶然命题”

“未来偶然命题”(future contingent proposition)是指“关于未来的偶然陈述，例如未来的事件、行为、状态等”*P.Øhrstrøm and P.Hasle，“Future Contingents”, The Stanford Encyclopedia of Philosophy，Retrieved from http：//plato.stanford.edu/archives/win2015/entries/future-contingent，2015，p.1.，亦即关于未来事件状态的既不必然真也不必然假的陈述。“我将去北京”、“明天将有海战”这样的命题可作为其标准实例。

在西方哲学史和逻辑史上，在对“未来偶然命题”的讨论中，有以下几种立场*P.Øhrstrøm，“In Defence of the Thin Red Line：A Case for Ockhamism”, Humana Mente 8，2009，p.20.：(1)不存在“未来偶然命题”，即关于未来的命题或者是不可能的，或者是必然的；(2)存在“未来偶然命题”，但没有“未来偶然命题”为真；(3)存在“未来偶然命题”，但它通常既不确定真也不确定假；(4)存在“未来偶然命题”，并且所有“未来偶然命题”都有真值(真或假)，尽管我们不知道它们的真值。第一种立场是一种决定论的观点，其余三种都是基于非决定论的观点。

在哲学中，关于未来偶然命题问题的讨论肇始于亚里士多德，他在《解释篇》第九章讨论了如何解释以下两个命题：“明天将有海战”和“明天将没有海战”。他说：“如果某事件明天既不会发生，又不会不发生，那就不会有偶然性的东西发生了。如某一‘海战’，以此为假设，那么它就会在明天既不会发生，也不会不发生。这些和另外一些不可能的结论就要产生，如果我们假定，在所有相互矛盾的两个命题中——全称或单称的肯定命题与否定命题——其一必然是真实的，另一必然是虚假的。所发生的事情就不可能是偶然的，一切事物的生成都是出自必然。”*亚里士多德：《亚里士多德全集》第一卷(中译本)，苗力田主编，北京：中国人民大学出版社，1990年，第58—59页。

对于“明天将有海战”和“明天将没有海战”这样的命题，我们应该说其真值在今天是不确定的吗？或者其中一个在今天为真而另一个在今天为假吗？这些问题的答案与对模态的解释有关。因为如果我们假定“明天将有海战”在今天为真，那么它在今天也不是必然的吗？进一步讲，如果结果是明天没有海战，那么“明天将有海战”在今天是可能的吗？在亚里士多德看来，根据非决定论，这两个命题在今天都不是必然的。然而，过去时态或现在时态的命题则不然，它们或者必然真或者必然假。因此，他是一个“过去决定论者”和“现在决定论者”，并且是一个“未来非决定论者”。*P.Øhrstrøm and P.Hasle，Temporal Logic：From Ancient Ideas to Artificial Intelligence，Studies in Linguistics and Philosophy(Kluwer，Dordrecht),1995，p.11.

中世纪某些神学家曾讨论过基于神学的未来偶然问题，可将其陈述如下：“根据基督教传统，上帝的预知被假定构成人类做出的未来选择的知识，但这显然导致从上帝的预知到未来必然性的简单论证：如果上帝现在已经知道我们明天将做的决定，那么关于我们明天选择的无法阻止的真在现在已经给出。”*P.Øhrstrøm and P.Hasle，“Modern Temporal Logic：The Philosophical Background”, in D.M.Gabbay and J.Woods(eds.),Handbook of the History of Logic，Vol.7, Logic and the Modalities in the Twentieth Century，Amsterdam：Elsevier,2006，p.463.这就否定了自由选择，或者说根本就不存在自由选择，即坚持上述决定论观点的立场(1)。

未来偶然性讨论引起的挑战是双重的：“首先，无论谁想要坚持某种关于未来的非决定论，他都可能要面临一些标准的赞成逻辑决定论的论证，即被设计来证明不存在未来偶然命题的论证。另外，任何赞成存在未来偶然命题的人都面临着建立一种合理且与开放未来观点相容的真理论的挑战。这种理论应该为下述问题提供答案：如果未来是开放的，我们能有意义地把未来偶然命题视为现在真或假的吗？如果能，如何赋值？关于偶然未来的断言有意义吗？如果有，在何种情况下有意义？”*P.Øhrstrøm and P.Hasle，“Future Contingents”, The Stanford Encyclopedia of Philosophy，Retrieved from http：//plato.stanford.edu/archives/win2015/entries/future-contingent,2015，p.3.

自亚里士多德以来的关于未来偶然命题的讨论绝不是一个简单的问题，它牵涉到哲学、逻辑学、神学等学科。未来偶然命题不但涉及“时态”，而且还可能涉及“模态”。从逻辑的角度看，应该如何刻画这样的命题？是否需要对未来偶然命题指派第三值？如果不需要，那么如何对这些命题赋值？三值逻辑和时态逻辑对这些问题进行了回答。

二、三值逻辑的处理方案

在20世纪20—30年代的一系列文章中，波兰逻辑学家卢卡西维茨(J.ukasiewicz)对亚里士多德关于未来偶然命题的讨论进行了特殊的解释，提出了“第三值”的思想。他说：“我可以无矛盾地假定：我在明年的某个时刻，例如在12月21日中午，出现在华沙，这在现在的时刻是不能肯定或否定地解决的。因此，我在所说的时间将在华沙，这是可能的但不是必然的。根据这个预先假定，‘我在明年12月21日中午出现在华沙’这句话在现时既不是真的，也不是假的。因为如果它现时是真的，那么我未来在华沙的出现就一定是必然的，而这与预先假定矛盾；如果它现时是假的，那么我未来在华沙的出现就一定是不可能的，而这也与预先假定矛盾。因此，所考虑的这句话在现时既不真也不假，必有与0(或假)和1(或真)不同的第三个值。我们可以用‘1/2’来表示这一点：它是‘可能的’(the possible)，作为第三个值是与‘假’和‘真’并行不悖的。这就是产生三值命题逻辑系统的思路。”*转引自威廉·涅尔、玛莎·涅尔：《逻辑学的发展》，张家龙、洪汉鼎译，北京：商务印书馆，1985年，第709页。这实际上遵循了上述立场(3)：存在“未来偶然命题”，因为未来事件尚未发生，所以可以认为这类命题在现在既不真也不假。在哈克(S.Haack)看来，卢卡西维茨的上述论证无效。因为它依赖于一种模态谬误：从(如果A那么B)是必然的，推出如果A，那么B是必然的。她进而得出结论：“即使宿命论是一种不能接受的论题，也没有必要用这种借口拒绝二值性。”*苏珊·哈克：《逻辑哲学》，罗毅译，北京：商务印书馆，2006年，第258页。

经典逻辑遵循二值原则：任一命题非真即假，不存在第三个真值。对二值原则最直接的拒斥是引入真和假之外的其他真值。卢卡西维茨通过引入第三个逻辑值“1/2”(解释为“可能的”或“不确定的”)来对“我在明年12月21日中午出现在华沙”这样的在说出它的时刻无法断定其真假的未来偶然命题赋值，进而构建三值逻辑。因此，如何理解第三值是卢卡西维茨三值逻辑的关键问题。为了处理第三值的情况，就必须对联结词进行重新解释。在经典逻辑关于命题联结词真值定义的基础上，卢卡西维茨对否定()和蕴涵(→)作了如下解释*转引自马利诺韦斯基：《多值逻辑》，张家龙译，载罗·格勃尔主编，张清宇、陈慕泽等译：《哲学逻辑》，北京：中国人民大学出版社，2008年，第350页。：

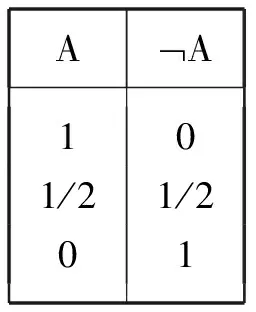
AØA101/21/201

→11/20111/201/2111/20111

很容易理解“可能的”命题的否定还是“可能的”命题。在对蕴涵的定义中，关于第三值命题的真值按如下方式确定：如果前件的值不大于后件的值，那么蕴涵式的值为1，否则为1/2。由此可定义其他的联结词析取()、合取()和等值(↔)的真值表*同上注。：

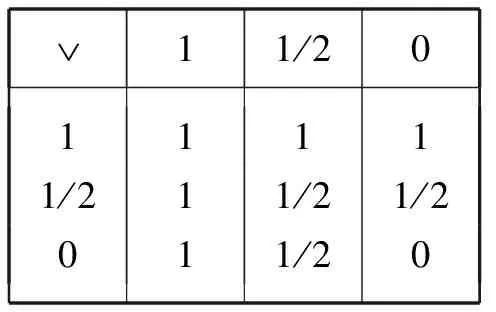
Ú11/2011111/211/21/2011/20

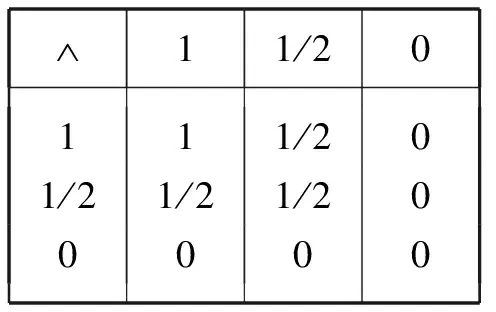
Ù11/20111/201/21/21/200000

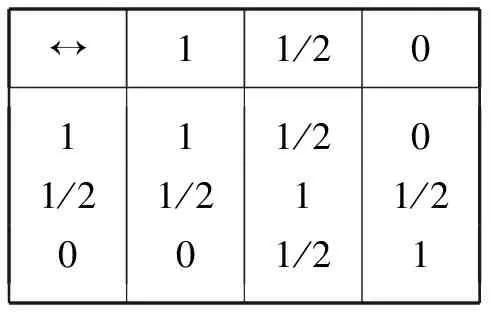
↔11/20111/201/21/211/2001/21

卢卡西维茨把那些恒取值1的公式定义为重言式。经典逻辑的重言式(pp)(矛盾律)，pp(排中律)不是卢卡西维茨三值逻辑的重言式。因为根据前面的真值表，当p取值1/2时，它们均取值1/2。对于两个关于未来的具有矛盾关系的命题的合取，对其指派真值1/2是反直观的。新西兰逻辑学家普赖尔(A.N.Prior)指出：“当我们严肃地考虑‘中性的’(即卢卡西维茨所谓的‘可能的’——引者注)命题的可能性时，这种逻辑具有一些非常反直观的特征。特别地，两个中性命题的合取是中性的，甚至在一个是另一个的否定的情况下。如果‘将有海战’是中性的或者不确定的，那么‘将没有海战’也应该是中性的或者不确定的无疑是合理的；但‘将有海战并且将没有海战’也应该是中性的或者不确定的无疑是不合理的——肯定地，它显然为假。另一方面，两个中性命题的合取自动为假同样不像是真实的，因为如果它们是独立的，那么它们的合取自然也应该是中性的。真值函项技术在这里似乎不合适。”*A.N.Prior，Past，Present and Future，Oxford：Clarendon Press,1967，p.135.因此，很难根据三值逻辑把中性命题的合取解释为“可能的”。诚如时态逻辑学家伯吉斯(J.P.Burgess)所评论的：“卢卡西维茨怀有偏见，总认为联结词‘非’、‘并且’等等也应当是取‘真’、‘假’、‘中’这三个值的真值函项联结词。这迫使他把亚里士多德和几乎所有古代和中古著述家都接受的矛盾律(pp)也拒绝掉了。”*伯吉斯：《不实在的将来》，载R.B.马库斯等著、康宏逵编译：《可能世界的逻辑》，上海：上海译文出版社，1993年，第198页。

就两个具有矛盾关系的未来偶然命题的析取而言，对其指派真值1/2也是有问题的。诚如普赖尔所言：“析取命题‘P或者非p’(明天将有海战或者明天将没有海战)不是一个偶然的而是一个必然的析取，它总是为真。但是，正如我们已经指出的，pp不是卢卡西维茨—塔斯基(A.Tarski)三值逻辑系统的规律。当p=0或1时，pp=1。但是，当p=1/2时，pp=1/2。”*A.N.Prior，“Three-Valued Logic and Future Contingents”, The Philosophical Quarterly，Vol.3，No.13,1953，pp.325-326.

其他的三值处理方法有类似的问题。例如，在克里尼(S.C.Kleene)的三值逻辑中，对可接受的算法无法确定其真假的或对实际的考察并不重要的命题指派第三个逻辑值U(“不定的”)。根据它的真值表，两个“不定的”命题的合取或析取同样是“不定的”。*马利诺韦斯基：《多值逻辑》，张家龙译，第354—357页。在波契瓦尔(D.A.Bochvar)的三值逻辑中，为了解决集合论悖论，把命题分为“有意义的”和“无意义的”或“悖谬的”。如果某一命题是真的或假的，那么它就是有意义的。真或假之外的命题都看成无意义的。根据它的真值表，两个“无意义”的命题的外合取或外析取为假。*马利诺韦斯基：《多值逻辑》，张家龙译，第357—358页。

当然，包括三值逻辑在内的多值逻辑有诸多方面的应用。例如，在证明经典命题演算公理独立性方面就用到三值和四值的赋值表*王宪钧：《数理逻辑引论》，北京：北京大学出版社，1998年，第104—107页。，而相干逻辑中重要元定理“相干原理”的证明则使用了八值的赋值表*冯棉：《相干逻辑研究》，上海：华东师范大学出版社，2010年，第30—31页。，如此等等。但就解释“未来偶然命题”，进而处理与之有关的推理而言，三值逻辑并不成功。

三、时态逻辑的处理方案

20世纪50年代，普赖尔仿效模态逻辑的做法，通过在经典命题演算和谓词演算的基础上添加几个时态算子(用过去算子P表示“曾有……情况”，用未来算子F表示“将有……情况”)和一些时态公理，构造了一系列时态逻辑系统。根据时间结构的不同，时态逻辑有线性、分支时态逻辑等之分。线性时态逻辑把时间看作一条线。线性包含向后(即过去)线性和向前(即未来)线性。前者是指对任意时刻t1、t2和t3，有t2

时态与模态的组合是很自然的，在古代就有第奥多鲁(Diodorus Cronus)根据时态定义模态。为了对“未来偶然命题”的真值和与之有关的推理提供新的处理方案，普赖尔提出了非决定论时态逻辑的奥卡姆主义系统，它是一种基于向前分支但向后线性的时态模态系统。向后线性，可形式化为“Pp→LPp”(L表示“必然……”)，意为“过去发生的事情都具有必然性”。它的度量时态逻辑版本是“Pmp→LPmp”(Pm表示“m个时间单位之前曾有……情况”)。

中世纪逻辑学家奥卡姆(W.Ockham)认为必须区分真正关于过去的命题与虚假关于过去的命题，他说：“曾有……情况，现在不可能不曾有……情况，这个原则仅仅应用于与未来时态命题不等值的过去时态命题(在等值的情况下，‘昨天曾有两天之后将有我在吸烟’等值于‘明天将有我在吸烟’——普赖尔注)。”*转引自A.N.Prior，Past，Present and Future，Oxford：Clarendon Press,1967，p.vi.因此，真正关于过去的真命题是必然的。换言之，在对Pp→LPp中的p作代入后，Pp一定要是真正关于过去的命题。把关于未来的真命题视为必然的是不合理的。普赖尔指出，这里的“必然”是指“现在无法阻止”(now-unpreventably)。*Ibid.，p.117.

在“Pp→LPp”(“如果曾有情况p，那么曾有情况p是现在无法阻止的”)或“Pmp→LPmp”(“如果m个时间单位之前曾有情况p，那么m个时间单位之前曾有情况p是现在无法阻止的”)这样的公式中，只要使用代入规则对p作代入就可得到含未来算子F的公式，例如，PFp→LPFp是Pp→LPp的代入实例。如何限制代入规则进而形式化这种方案？普赖尔认为可以基于把命题分为“在其中没有未来痕迹的命题”(即真正关于过去以及现在的命题)和关于未来的命题两类。就后一类命题而言，即使是在现在它们也有确定的真值“真”或“假”，只是我们不知道。他建议在形式化时可以使用a、b、c等表示前一类命题，而用p、q、r等代表任何时态命题。为了限制代入规则，他定义了该系统的公式的一个子类“A公式”，它只能使用前一类变元。在使用代入规则时，可以用任一公式对后一类变元作代入，但只能用真正关于过去和现在的公式对前一类变元作代入。*Ibid.，pp.123-125.此外，他讨论了另一种只使用a、b、c等变元的形式化。

普赖尔把基于上述观点构筑的逻辑称为“奥卡姆主义逻辑”。他讨论了只使用a、b、c等变元的奥卡姆主义系统的语义模型，他说：“我们可以把一个奥卡姆主义模型定义为没有开端或者终点的线，它从左向右(即从过去到未来)移动时可以分支(branches)，尽管不是相反；因此，从线上的任何一点只有一条路径(route)通向左边(即过去)，但可能有许多可选择的通向右边(即未来)的路径。”*A.N.Prior，Past，Present and Future，Oxford：Clarendon Press，1967, p.126.显然，这个模型是向后线性、向前分支的。这种语义的特点在于任一公式在一个时刻的真值依赖于通过该时刻的“分支”、“路径”或所谓的“编年史”(chronicle)或“历史”(history)的选择。不难发现，这与上述立场(4)相吻合：存在“未来偶然命题”，并且所有“未来偶然命题”都有真值(真或假)，尽管我们现在还不知道它们的真值。

可以把这个系统的模型呈现如下*参见P.Øhrstrøm and P.Hasle，“Modern Temporal Logic：The Philosophical Background”, in D.M.Gabbay and J.Woods(eds.),Handbook of the History of Logic，Vol.7, Logic and the Modalities in the Twentieth Century，Amsterdam：Elsevier,2006，pp.467-468； P.Øhrstrøm，In Defence of the Thin Red Line：A Case for Ockhamism，Humana Mente 8,2009，pp.24-26； P.Øhrstrøm and P.Hasle，Future Contingents，The Stanford Encyclopedia of Philosophy，Retrieved from http：//plato.stanford.edu/archives/win2015/entries/future-contingent,2015，pp.25-29。：一个奥卡姆主义模型是一个有序四元组〈TIME，≤，C，V〉。其中〈TIME，≤〉是偏序时刻集，TIME是一非空集合，可称为时刻集，≤(“不晚于”)是TIME上的一个偏序关系。对于TIME中的任意时刻t和t′，若t≤t′且t≠t′，则t

(1) V(t，c，a)=1当且仅当T(a，t)=1，其中a是任一关于过去或现在的命题变元。

由V满足的上述条件可推知其他算子的赋值条件，其中可能算子M的赋值条件为：

V(t，c，A)可以读作“A在分支c中的时刻t为真”。一个公式A是“奥卡姆主义有效的”当且仅当对任一赋值函数T和任一奥卡姆主义模型〈TIME，≤，C，V〉中的任一分支cC中的任一时刻tc，都有V(t，c，A)=1。可以添加一个区间函数得到奥卡姆主义模型中赋值的度量版本，用d(t′，t″，m)表示“t′在t″的m个时间单位之前”，其中t′和t″属于同一分支，m为正数，使用这个函数(4)和(5)分别替换为：

从常识和自然语言观点看，奥卡姆主义系统对“FmA，LFmA和MFmA”这三者的区分是很有吸引力的。例如，我们不但可以谈论“明天将有海战”，还可以谈论“必然(在所有可能的)明天将有海战”和“可能(在某一可能的)明天将有海战”。*参见P.Øhrstrøm，“Time and Logic：A.N.Prior’s Formal Analysis of Temporal Concepts”, S.Ferré and S.Rudolph (Eds.)：ICFCA 2009，LNAI 5548，pp.75-76。奥卡姆主义逻辑在用户与计算机系统互动研究中有一个有趣的应用：一个基于普赖尔的奥卡姆主义时态逻辑的模型可以解释为包含一个动态的计划，即包含相应于由考虑之中的人做出的任何可能选择的替代计划。这意味着：当存在可选择的未来时，这个模型至少应该包含默认的选择或者建议的选择，即给用户的一个建议。这个计划应该导致用户获得在给定选择下的最佳可能的结果。*Ibid.，p.77.

四、进一步的思考

时间是一个奇特的概念。尽管关于时间没有统一的观点，但富有成效的研究是可能的。对未来事件的决定论与非决定论的讨论，刻有神学或科学的印记。决定论者认为未来发生的每件事都是已经发生的某件事的无法避免的后果。非决定论者则认为未来的某些方面并非已经发生之事的不可避免的后果。如果说决定论者把时间看作一条线，那么非决定论者则是把它看作向未来分支的一组岔路。*伯吉斯：《不实在的将来》，载R.B.马库斯等著，康宏逵编译：《可能世界的逻辑》，上海：上海译文出版社，1993年，第192页。

尽管分支时间的本体论地位存在争议，但从逻辑的观点看，普赖尔基于分支时间的奥卡姆主义逻辑对关于未来偶然命题的真理论提供了一种较好的处理方法。就对于未来偶然命题的解释而言，较之于卢卡西维茨的第三值处理法，笔者倾向于赞同普赖尔的奥卡姆主义处理方案。理由大致如下：(1)三值逻辑为了坚持非决定论而抛弃二值原则，但按照时态模态逻辑，在二值原则的基础上同样可以坚持非决定论。因此，根据奥卡姆剃刀原理：“如无必要，勿增实体”，引入第三值是不必要的。(2)笔者以为未来偶然命题在现在是有真假的，只是作为人类的我们不知道罢了。(3)过去已经记录在案，现在正在亲身感受，它们都是不可改变的。而未来就不同了，在某种意义上它可以为我们存在。换言之，未来的事件进程可能不止一种。因此，如果时间是分支的，那么进入未来就有多种不同的路径。根据不同的路径来解释未来偶然命题，进而把“未来”与“必然”和“可能”等模态联系起来是符合日常表达习惯的。

前面已谈及“未来偶然命题”讨论中的立场(1)、(3)和(4)，它们分别对应于中世纪某些神学家的观点、卢卡西维茨的三值逻辑方案和普赖尔的奥卡姆主义方案。最后谈谈立场(2)：未来偶然命题在现在为假吗？普赖尔在《过去、现在和未来》一书中作了讨论，他用对“区间n之后将没有情况p”(it will not be the case the interval n hence that p)的两种含义的明确区分来代替第三真值。在他看来，这个命题可能意味着：“(1)区间n之后将有并非p(It will be the case the interval n hence that(it is not the case that p))，即Fnp；或者(2)并非区间n之后将有情况p(It is not the case that(it will be the case the interval n hence that p))，即Fnp。”*A.N.Prior，Past，Present and Future，Oxford：Clarendon Press,1967，p.129.他接着指出：“这里的‘将’(will)意味着‘一定将’(will definitely)，直到在某种意义上确定将有情况p，‘将有情况p’才是真的；直到在某种意义上确定将有并非p，‘将有并非p’才是真的。如果不这样解决这些问题，所有这些断言，即Fnp和Fnp仅仅为假。”*同上注。需要注意的是，普赖尔认为未来偶然命题在现在具有真值假，进而认为未来排中律“FnpFnp”不成立，这是与他的非决定论和自由选择假定分不开的。