Correlating thermal conductivity of pure hydrocarbons and aromatics via perceptron artificial neural network(PANN)method

Mostafa Lashkarbolooki*,Ali Zeinolabedini Hezave ,Mahdi Bayat

1 School of Chemical Engineering,Babol University of Technology,Babol,Iran

2 Islamic Azad University,Dashtestan Branch,Borazjan,Iran

3 Department of Chemical Engineering,Faculty of Engineering,University of Bojnord,Bojnord,Iran

1.Introduction

Thermal conductivity is the ability of a material to conduct heat which is known as a crucial transport property related to heat transfer process calculations.For hydrocarbon systems,accurate knowledge of such properties is necessary to appropriately design equipments in petroleum production,processing and related industries.Even for the specific liquid at the specific temperature,the experimental thermal conductivity measured by different investigators does not seem satisfactory[1,2].In addition,not only thermal conductivity is a difficult property to be measure but also there are many thousands of possible liquids that make it impossible to measure the thermal conductivity of them experimentally.

Regarding this shortcoming,many investigators tried to find reliable predictive tools.The first effort was using theoretical methods which yielded no enough accuracy and simple expressions for calculating the thermal conductivity of liquids.After that,several researchers proposed correlation based on empirical or semi-theoretical method widely employed over limited ranges of temperature[3–6].More recently correlations are proposed by Jamieson[7,8],Teja and co-workers[9–11],Klaas and Viswanath[12],and Lei and co-workers[13,14].Although,these correlations have been proposed,working not willingly makes the researchers look for more accurate correlations and techniques.Based on this fact,some researchers have focused on prediction of thermal conductivities of both gases and liquids using group contribution methods.The results obtained from the group contribution methods show a better flexibility,although these methods suffer some limitations move the researchers toward finding new predictive methods and tools.

In this direction,artificial neural network(ANN)was utilized in this study to correlate the thermal conductivity of the liquid hydrocarbons if normal and aromatic since there is no reported attempt using this method based on the best knowledge of the authors.

In more details,the purpose of the present work is developing a neural network model to predict the thermal conductivity of pure liquids at different temperatures while the pressure is atmospheric.

2.Predictive Tools

There exist a variety of methods and techniques allowing for correlating and predicting the physio-chemical properties of liquids[15].As aforementioned,due to lack of knowledge about the thermal conductivities,predicting,estimating and correlating the thermal conductivity of different liquids seem a crucial criterion in the field of chemistry and chemical engineering.Generally,the predictive methods can be outlined and categorized as follows.

2.1.Simple and general correlations

Milletet al.[16]suggested following form of correlation:

whereA,BandCare constant parameters obtained using simple regression method.Unfortunately the proposed correlation by Milletetal.[16]is just applicable for the prediction of thermal conductivity at isochoric conditions or data along the vapor–liquid orsolid–liquid saturation line.Considering that,one can predict the thermal conductivity of liquids if he/she considers both the effects of temperature and pressure[17].

Besides,general correlations are based on one or more properties of pure components such as molar mass,liquid density,heat capacity at constant pressure,heat of vaporization or the normal boiling point[18–21].A comprehensive comparison performed by Horvath[18]revealed that the empirical model by Sato and Riedel[19]which required the temperature,critical temperature,and molecular weight for prediction of thermal conductivity of any organic compound is the best general correlation.

2.2.Family methods

In these methods,predictive equations are obtained by regression of experimental data according to the chemical family such as Latiniet al.[22].The point that must be pointed out is that the applicability of the methods depends on the definition of the chemical family.The most important drawback of these methods is their limitation to be used only for the chemical families which the models were developed.

2.3.Group contribution methods

These methods are similar to the family methods,but are much more widely applicable if the groups are well de fined.Model parameters are fitted to the groups,which make up the compounds.Two of the available group contribution methods have been implemented below.

2.3.1.Nagvekar and Daubert method

One of the first group contribution methods proposed to predict the thermal conductivity is Nagvekar and Daubert method[23].This method is based on the second order contribution scheme as set out by Benson and Buss[24],which followed “nearest neighbor interactions”theory.In addition,they have utilized the temperature dependent equation of Reidel(Eq.(2))proposed in 1951 as a basis for their group contribution model.

In the above equation,λ is the liquid thermal conductivity,Trthe reduced temperature,andAis a regressed constant dependent upon the class of liquid.Then,the above Eq.(2)was modified to Eq.(3)by Nagvekar and Daubert[23]as below:

whereAandB,are the group contribution parameters.But,this method is limited to the temperature range of 0.3＜Tr＜0.9.

2.3.2.Sastri and Rao

During 1993 Sastri and Rao[25]proposed more applicable method compared to other group contribution methods correlates more wider range of organic liquids.It can correlate thermal conductivity of the liquid from the triple point to a reduced temperature of 0.95.But,the most important advantage of this method was related to this point that it considers the normal boiling point temperature as a reference temperature instead of the critical temperature usually considered.The model used was based on experimental data for 37 organic liquids by Miller[26].They have proposed two different relationships,predicting the thermal conductivity of the liquids both below and above the boiling point temperatures described as follows:

where,λBis the thermal conductivity at the normal boiling point and is calculated using group contributions.

2.4.Corresponding states methods

The theory of corresponding states,states that all fluids,when compared at the same reduced temperature and reduced pressure,have approximately the same compressibility factor and all deviate from ideal gas behavior to about the same degree.The corresponding states methods are especially well-known for hydrocarbons although it does not work willingly for more complex compounds with sufficient reliability.

2.5.Artificial neural network(ANN)

Recently,a new smart method called neural networks has been used extensively to predict different parameters in various fields of engineering in particular physio-chemical properties utilized in chemical engineering[27–36].The extensive application of this method rises from its unique capability to model very complicated and multi-variable dependent processes.

For example,Turiaset al.[37]studied the application of pattern recognition and artificial intelligence techniques in the characterization of a multi-phase realistic disordered composite and in a design of a multiple regression model to estimate effective thermal conductivity.Additionally,Sablani and Rahman[38]presented an ANN model to predict thermal conductivity of food as a function of moisture content,temperature and apparent porosity.The model was able to predict thermal conductivity with a mean relative error of 12.6%.Also,Eslamloueyan and Khademi[39]developed a feed-forward three-layer neural network based on the critical temperatures,critical pressures and molecular weights of compounds to predict the thermal conductivity of pure gases at atmospheric pressure over a wide range of temperatures.Moreover,Boozarjomehriet al.[40]characterized the basic properties of pure substances and petroleum fractions by a neural network.

Furthermore,Hezaveet al.[41]proposed a perceptron neural network for the prediction of the ternary electrical conductivity of the mixtures containing ILs.They have been reported that the proposed network was able to accurately predict the electrical conductivity of the ternary mixtures with an acceptable level of deviation using molecular weight and melting point as a substance discriminator.

2.5.1.Methodology

The ANN model similar to any other predicting methods needs a series of reliable and wide range experimental data points to find its fitting parameters.In the light of 956 experimental data points on the thermal conductivity of the liquid hydrocarbons and aromatics were collected from the previously published literature[42–45].The physiochemical properties including critical temperature and pressure and acentric factor of the used compound are given in Table 1[3].

Amore detailed description of the proposed method has been previously reported by Hezaveet al.[41].The schematic of the used ANN in this study is given in Fig.1.

Table 1Physical properties of the pure liquids

In this study,three independent variables including reduced temperature of the system(Tr=T/Tc),reduced pressure(Pr=P/Pc)and acentric factor(ω)are considered as an input of the input layer.Acentric factor,critical temperature(Tc)and critical pressure(Pc)were utilized to differentiate the liquids.Using the reduced form of temperature and pressure leads to a reduction in the number of independent variables of the ANN model from five to three.The feasibility of using reduced temperature of the system,critical pressure and acentric factor as independent variables of ANN model was previously examined and validated for prediction of vapor–liquid equilibria[46].

In brief,ANNs are nonlinear learning mathematical models that are designed in the second half of the twentieth century by simulation of human brain procedures and have been used in many scientific areas till now[47].The strength of this method rises from the capability of these networks to correlate inputs and outputs of most nonlinear multi-variable systems with any complexities.

These networks consisted of a number of simple processing units that are connected together in a specified manner according to the type of the network.These processing units have inspired from biological neurons,and are called artificial neurons.The available data fed into the input layer,then dispatched through the hidden layer and after being processed sent to the output layer where the desired values displayed.The output of a neuron can be computed from Eq.(6):

where the input signals to each neuron are weakened or strengthened through their multiplication to weight coefficients(wjr).The biases(bj)are activation thresholds that are added to the production of inputs(xr)and their particular weight coefficients[48].

Besides the weight and biases which must be optimized,transfer functions and the number of neurons in the hidden layer are important parameters that must be also optimized.In the present study,trial and error procedure was used for training stage previously described in detail elsewhere[41].

Generally,the available experimental data were randomly divided into two sets namely training and testing sets[35].The training set was used to find the proper network structure while the testing set which was not considered in the training stage was used to examine the applicability of the proposed network to correlate the thermal conductivity of the liquids.

The point that must be mentioned is that although the training subset is randomly selected,it is selected in a way that includes all the ranges of the experimental conditions.In addition,to examine the extrapolative capability of this model,some collected data are not included in the training subset to directly correlate them in the testing stage.In other words,using these unseen data during the training subset,it is possible to examine the extrapolative capability of the proposed neural network.

Fig.1.The schematics of used feed-forward MLP for prediction of thermal conductivity of pure liquid.

To clearly investigate the functionality of the proposed network different statistical parameters including average absolute relative deviation percent(AARD),mean square error(MSE),average absolute deviation(AAD),average deviation(AD),minimum deviation(MinD),maximum deviation(MaxD),average relative deviation percent(ARD)and correlation coefficient(R2)were used.The equations of the used statistical parameters are given through Eqs.(7)to(14).

where,λexpis the experimental thermal conductivity,λcalis the calculated oneviaANN model and¯λ is the average thermal conductivity.

It should be mentioned that the used ANN model utilized AARD,MSE andR2values for optimization while the other statistical parameters(Eqs.(10)–(14))were used only to ease comparison between the obtained results with the proposed ANN model and the results of the other predictive methods.

3.Results and Discussion

In the present investigation,the ANN model is used to correlate the thermal conductivity of the normal and aromatic liquid hydrocarbon in a wide range of temperature.Comparing the obtained results with the other predictive methods,it can be concluded that not only this method enables to correlate thermal conductivities with acceptable error but also it can extrapolate the thermal conductivity very well.

Generally,using trial and error procedure coupling with the statistical parameters previously mentioned leads to considering log-sigmoid and linear(purelin)(Eqs.(15)and(16))as the best transfer functions for the hidden and output layers,respectively.

The good ability of the proposed network to accurately correlate the thermal conductivity rises from the nonlinearity,continuity and differentiability nature of aforementioned functions.This nature enables the neuromorphic model to relate input and output data with any complexity.The differentiability of these transfer functions is an important characteristic,which allows the gradient-based training algorithms to update the weights and biases.

In addition,the obtained results obviously showed that the optimum network architecture must be consisted of three layers namely input,hidden and output in which 22 neurons in the hidden layer are needed.The results of the different topology examination to find the optimum number of neurons in the hidden layer are shown in Fig.2.In addition,the weight and bias of the best ANN structure(i.e.ANN with 22 neurons)are listed in Table 2.

Fig.2.Results of topology studies to find the optimal ANN con figuration.

Table 2The weight and bias of the proposed ANN model

A parity plot of the experimental and predicted thermal conductivity values using the ANN model with optimum con figuration has been shown in Fig.3.As it can be seen,the solid line shows the best fit of the experimental data with predicted values and star points are the predicted values.A close examination in Fig.3 revealed that the thermal conductivity data are quite well fitted with the best fit curve.The results of the training evaluation indicated that the AARD,MSE andR2for the proposed ANN are 0.20%,1.05×10−7and 0.9994,respectively.In addition,the predicted values of thermal conductivity data points in the test stage were compared with the experimental ones in Fig.4.The results of statistic analysis for test data indicated that the AARD,MSE andR2for the proposed ANN are 0.20%,1.07×10−7and 0.9994,respectively.Totally,based on results is demonstrated in Figs.3 and 4,one can find that the ANN model is an applicable tool to be used as a predictive method for the thermal conductivity correlation techniques.

In addition,detailed presentations of the obtained results of ANNfor training and test data are depicted in Figs.5 and 6,respectively.These figures showed both the experimental and predicted ones by ANN modelversustemperature for all pure liquids.It is completely obvious that,the proposed ANN model predicted the thermal conductivity of pure liquids over a wide range of temperature in an acceptable level of engineering deviation.

Also,a very detailed list of the obtained results through the calculated different statistical error parameters is given in Table 3 one can analyze the sensitivity and accuracy of the proposed ANN model for different families including alkenes,n-alkanes,aromatics,cycloalkanes,cycloalkenes,isomers of alkanes andn-alkanes types in wide range of temperature.It is completely clear that considering the error analysis the ANN model is a very useful and accurate method for thermal conductivity prediction.

Finally,the obtained results through the ANNmodel were compared to the different available correlations and group contribution methods.In the first attempt,the obtained results for cyclohexane,n-Pentane,n-Decane,methylcyclopentane and benzene were compared to six different methods namely Latiniet al.,Sato–Riedel,Missenard–Riedel,Klaas–Viswanath[12],Nagvekar–Daubert and Rodenbushet al.[49]methods.

The obtained results given in Table 4 demonstrated a rather good predictive capability of the proposed ANN model compared to the other methods previously proposed.The point should be considered is that the ANN models are generally working willingly in the range which were trained,but here forn-decane at 349 K and benzene at 389 K,which were out of the training range,the deviation of the prediction results is lower than 2.50%which somehow shows the possible extrapolative capability of the proposed ANN model.

In addition,the results of the ANN model were compared to other predictive models including the Jamieson equation[7],the modified Reidel equation[7]and the recent models proposed by Klaaset al.[12]and Leietal.[13](see Table 5).Aglance on the obtained results illustrated a relative good capability of the ANN model to correlate the thermal conductivity values compared to the other previously proposed methods.Although,a glance revealed that the proposed ANN model correlates the thermal conductivity more accurately,the worth mentioning point must be carefully considered is that the temperature range which the modified Reidel equation[7],Jamieson equation[7],Wanget al.[1],Klaaset al.[12]and Leiet al.[13]are used is wider(192–613 K)than the temperature range(257–330 K)used in the current investigation.

Fig.3.Plot of experimental thermal conductivity data vs.proposed ANN prediction for training.

Fig.4.Plot of experimental thermal conductivity data vs.developed ANN prediction for testing.

Fig.5.Experimental and the proposed ANN model vs.temperature for all pure liquid which was used for training stage.

Fig.6.Experimental and the proposed ANN model vs.temperature for all pure liquid which was used for test stage.

Also,the obtained results were compared with the correlation proposed with Riaziet al.[50]and Vasquez–Briano method[51](see Tables 6 and 7).The comparisons showed that the ANN modeland both of the methods work with an acceptable accuracy.But,closer examination in Tables 6 revealed that although the number of data used foreach component is higher by the ANN model compared with the Riaziet al.[50]method,it should be considered that the Riaziet al.[50]utilized a wider range of temperature for each component.

Considering this,the higher AAD of Riaziet al.[50]compared with the AAD of the proposed ANN model can be related to the wider rangeof temperature for prediction.In contrast,in Table 7 it is obvious that the Vasquez–Briano method[51]have used larger data bank automatically leads to a higher percentage of error.

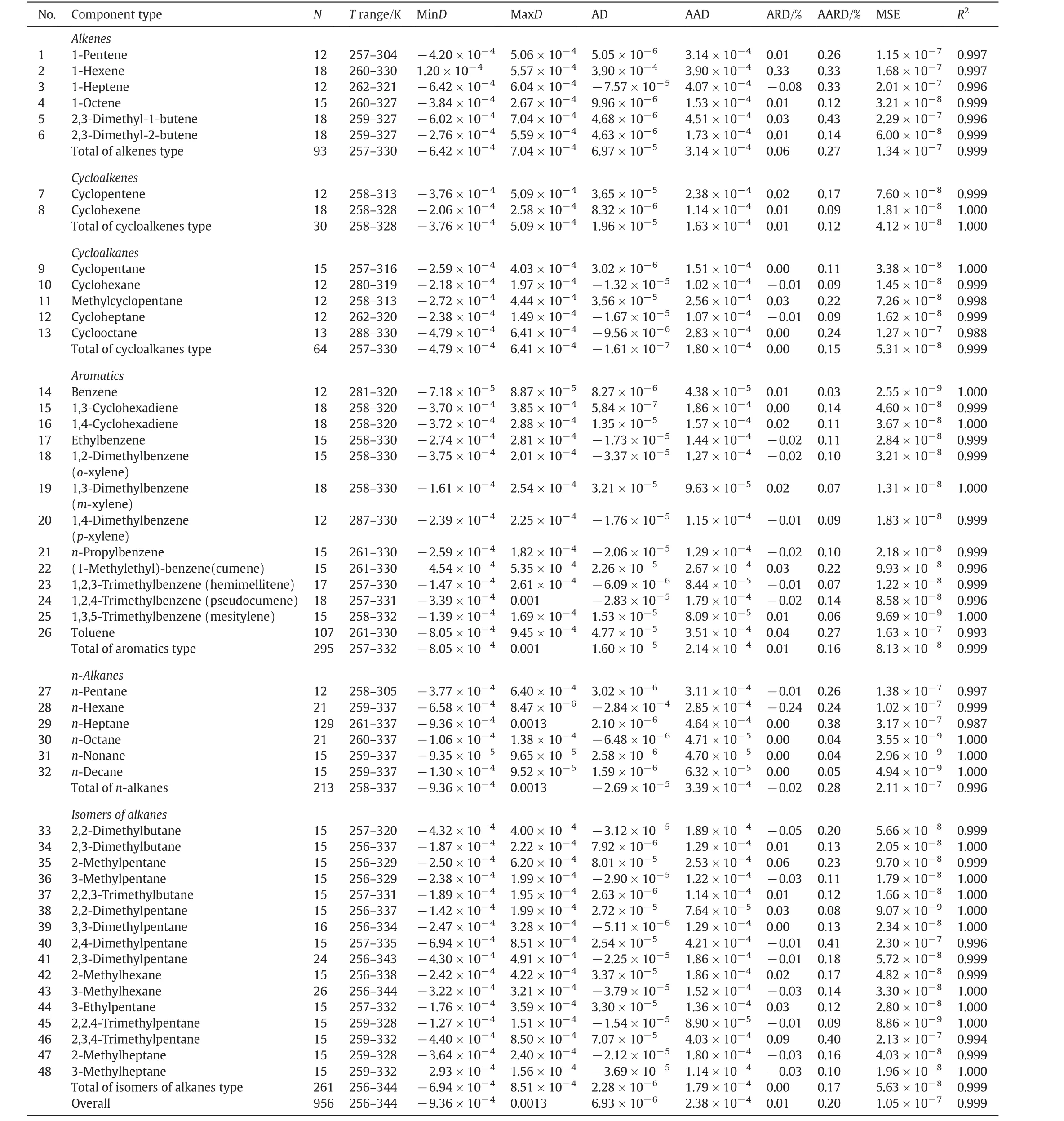
Table 3The overall obtained results of thermal conductivities for the different families

Finally,the results of the ANN model for the thermal conductivity prediction were compared with the two equations of Pachaiyappanet al.[52]and Riazl and Faghri method[53].It must be considered that methods of Pachaiyappanet al.[52]were recommended as the best methods available for predicting thermal conductivity of liquids and vapors,respectively,by the American Petroleum Institute[53].The proposed equation for thermal conductivity of liquids by Pachaiyappanet al.[52]is in the following form:

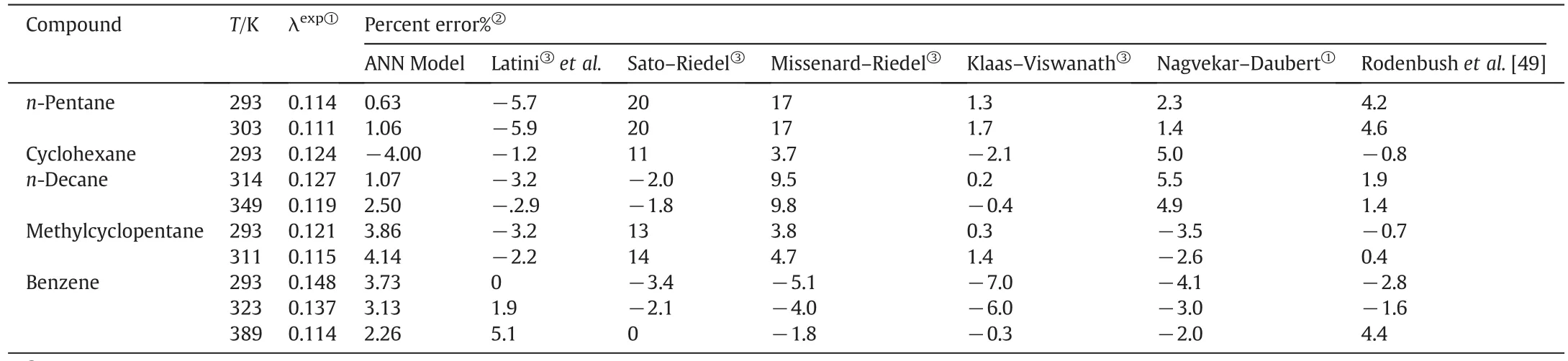
Table 4Comparison between the ANN model results and other predictive methods

Table 5Comparison between the obtained results with ANN and the other available predictive methods

Table 6Comparison between the results of the Riazi et al.[50]and ANN model

Table 7Comparison between the obtained results with ANN and those obtained with Vasquez–Briano method[51]

The results of these comparisons given in Table 8,demonstrated that the ANN model predicted the thermal conductivity of the liquids with an acceptable level of engineering accuracy compared with the other two methods namely Pachaiyappanet al.[52]and Riazl and Faghri methods[53].But,it should be enlightened that Pachaiyappanet al.[52]and Riazl and Faghri methods[53]are for the thermal conductivity prediction of both vapor and liquids while the ANN model only predicts the liquid status of the hydrocarbon and aromatics.In addition,the proposed method by Pachaiyappanet al.[52]and Riazl and Faghri method[53]are applicable for wider families of the hydrocarbons.By the way,it can be claimed that for the investigated families of hydrocarbons(see Table 1);the ANN method is more accurate.

In total,considering all of the obtained results one can conclude that although the proposed ANN model is trained,validated and tested in a narrower temperature range compared with the other available methods,not only it is highly accurate in the examined range(minimum AARD of 0.03%),but also it can accurately extrapolate the thermalconductivity data of hydrocarbon with an acceptable level of engineering introducing an amazing capability to the proposed ANN model.

Table 8Comparison between the ANN model and Pachaiyappan et al.[52]and Riazl and Faghri method[53]

4.Conclusions

In the present study,an ANN based model was proposed to correlate the thermal conductivity of the normal and aromatic liquid hydrocarbons.In the first stage,956 experimental thermal conductivity data were collected from different published literature to verify the ANN model.In addition,the collected data were divided into two different subsets in which the first subset was used to optimize the parameters of the network including weight,biases,number of layers,number of neurons in the hidden layer and transfer functions for the hidden and output layers.In this way,a trial and error approach was used to which leads to find the logarithmic sigmoid and purelin transfer functions as the optimum functions for the hidden and output layers,respectively.Further analysis revealed that the best number of neurons in the hidden layer was twenty two neurons.Generally,based on the obtained results oferror analysis,it is completely obvious that the ANN model was able to accurately correlate the thermal conductivity of the liquid hydrocarbons.In details,results demonstrate that the proposed ANN model accurately predicts the thermal conductivity of alkenes,n-alkanes,aromatics,cycloalkanes,cycloalkenes,aromatics,isomers of alkanes andn-alkanes type components as evident from the AARD,MSE andR2,which were 0.20,1.05×10−7and 0.9994,respectively.

For further investigation,the obtained results using proposed neural network were compared with number of methods including correlations and group contribution methods.Although the biggest advantage of that method was their generality for different families of chemicals,the ANN model correlates the thermal conductivity of the normal and aromatic liquid hydrocarbons with a high level of accuracy(minimum AARD of 1.53×10−4).The other interesting capability of the proposed neural network was it extrapolative capability besides its correlative capability which can make ita promising method to predict the thermal conductivity of the liquid hydrocarbons and aromatics.

[1]F.A.Wang,J.Q.Zhu,H.S.Chen,W.C.Wang,Y.L.Jiang,A new model of thermal conductivity for liquids,Chem.Eng.J.78(2000)187–191.

[2]M.R.Riazi,G.A.Enezi,S.Soleimani,Estimation of transport properties of liquids,Chem.Eng.Commun.176(1999)175–193.

[3]R.C.Reid,J.M.Prausnitz,B.E.Poling,The Properties of Gases and Liquids,4th edition McGraw-Hill,New York,1987.

[4]M.Moetamast,Viscosity and Thermal Conductivity,Masukaza yakata,Tokyo,1975.

[5]V.S.Touloukian,P.E.Liley,S.C.Saxena,Thermal Conductivity,Nonmetallic Liquids and Gases,Plenum Press,New York,1970.

[6]F.A.Wang,Introduction to Chemical Engineering Data,Chem.Ind.Press,Beijing,1979.

[7]D.T.Jamieson,Thermal conductivity of liquids,J.Chem.Eng.Data24(1979)244–246.

[8]D.T.Jamieson,G.Cartwright,Thermal conductivity of associated liquids,J.Chem.Eng.Data25(1980)199–201.

[9]A.S.Teja,P.Rice,A generalized corresponding states method for the prediction of the thermal conductivity of liquids and liquid mixtures,Chem.Eng.Sci.36(1981)417–422.

[10]A.S.Teja,G.Tardieu,Prediction of the thermal conductivity of liquids and liquid mixtures including crude oil fractions,Can.J.Chem.Eng.66(1988)980–986.

[11]J.G.Bleazard,A.S.Teja,Extension of the rough hard-sphere theory for transport properties to polar liquids,Ind.Eng.Chem.Res.35(1996)2453–2459.

[12]D.M.Klaas,D.S.Viswanath,A correlation for the prediction of thermal conductivity of liquids,Ind.Eng.Chem.Res.37(1998)2064–2068.

[13]Q.Lei,Y.C.Hou,R.Lin,A new correlation for thermal conductivity of liquids,Chem.Eng.Sci.52(1997)1243–1251.

[14]Q.Lei,R.Lin,D.Ni,Thermal conductivities of some organic solvents and their binary mixtures,J.Chem.Eng.Data42(1997)971–974.

[15]S.A.Shojaee,S.Farzam,A.Z.Hezave,M.Lashkarbolooki,S.Ayatollahi,A new correlation for estimating thermal conductivity of pure ionic liquids,Fluid Phase Equilib.354(2013)199–206.

[16]J.Millet,J.H.Dymod,C.A.Nieto de Castro,Transport Properties of Fluids—Their Correlation,Prediction and Estimation,Cambridge University Press,New York,2005.

[17]V.G.Nemzer,L.V.Nemzer,V.V.Pugach,Thermal conductivity of poly(ethylsiloxane)liquids at high pressures,J.Chem.Eng.Data41(1996)848–851.

[18]A.L.Horvath,Molecular Design—Chemical Structure Generation from the Properties of PureOrganic Compounds,Elsevier,New York,1992.

[19]R.C.Reid,J.M.Prausnitz,B.E.Poling,The Properties of Gases and Liquids,4th ed.McGraw-Hill,New York,1987.

[20]D.S.Lakshmi,D.H.L.Prasad,A rapid estimation method for thermal conductivity of pure liquids,Chem.Eng.J.48(1992)211–214.

[21]P.M.Mathias,V.S.Parekh,E.J.Miller,Prediction and correlation of the thermal conductivity of pure fluids and mixtures,including the critical region,Ind.Eng.Chem.Res.41(2002)989–999.

[22]G.Latini,P.Pierpaoli,P.F.,Dynamic viscosity and thermal onductivity prediction of refrigerants and refrigerant mixtures,International Refrigeration and Air Conditioning Conference 1992,pp.489–498.

[23]M.Nagvekar,T.E.Daubert,A group contribution method for liquid thermal conductivity,Ind.Eng.Chem.Res.26(1987)1362–1365.

[24]S.W.Benson,J.H.Buss,Additivity rules for the estimation of molecular properties.Thermodynamic properties,J.Chem.Phys.29(1958)546–572.

[25]S.R.S.Sastri,K.K.Rao,Quick estimating for thermal conductivity,Chem.Eng.100(1993)106–107.

[26]J.W.Miller Jr.,R.S.Gordon,C.L.Yaws,Correlation constants for chemical compounds-thermal conductivity of gas,Chem.Eng.83(25)(1976)153–155.

[27]G.Carrera,J.Aires-de-Sousa,Estimation of melting points of pyridinium bromide ionic liquids with decision trees and neural networks,Green Chem.7(2005)20–27.

[28]L.Jianfei,L.Weitie,C.Xiaolong,L.Jingyuan,Optimization of fermentation media for enhancing nitrite-oxidizing activity by artificial neural network coupling genetic algorithm,Chin.J.Chem.Eng.20(2012)950–957.

[29]N.Bar,T.K.Bandyopadhyay,M.N.Biswas,S.Kumar Das,Prediction of pressure drop using artificial neural network for non-Newtonian liquid flow through piping components,J.Pet.Sci.Eng.71(2010)187–194.

[30]M.Lashkarbolooki,Z.S.Sha fipour,A.Z.Hezave,Trainable cascade-forward backpropagation network modeling of spearmint oil extraction in a packed bed using SC-CO2,J.Supercrit.Fluids73(2013)108–115.

[31]S.Nasseh,A.Mohebbi,Z.Jeirani,A.Sarra fi,Predicting pressure drop in venturi scrubbers with artificial neural networks,J.Hazard.Mater.143(2007)144–149.

[32]M.Lashkarbolooki,A.Z.Hezave,S.Ayatollahi,Viscosity prediction of ternary mixtures containing ILs using multi-layer perceptron artificial neural network,Fluid Phase Equilib.326(2012)15–20.

[33]I.Jahanandish,B.Salimifard,H.Jalalifar,Predicting bottomhole pressure in vertical multiphase flowing wells using artificial neural networks,J.Pet.Sci.Eng.75(2011)336–342.

[34]S.K.Lahiri,K.C.Ghanta,Development of an artificial neural network correlation for prediction of hold-up of slurry transport in pipelines,Chem.Eng.Sci.63(2008)1497–1509.

[35]M.Lashkarbolooki,A.Z.Hezave,A.Babapoor,Correlation of density for binary mixtures of methanol+ionic liquids using back propagation artificial neural network,Korean J.Chem.Eng.30(2013)213–220.

[36]F.Youse fi,Z.Amoozandeh,Statistical mechanics and artificial intelligence to model the thermodynamic properties of pure and mixture of ionic liquids,Chin.J.Chem.Eng.24(12)(2016)1761–1771.

[37]I.J.Turias,J.M.Gutiérrez,P.L.Galindo,Modelling the effective thermal conductivity of an unidirectional composite by the use of artificial neural networks,Compos.Sci.Technol.65(2005)609–619.

[38]S.S.Sablani,R.M.Sha fiur,Using neural networks to predict thermal conductivity of food as a function of moisture content,temperature and apparent porosity,Food Res.Int.36(2003)617–623.

[39]R.Eslamloueyan,M.H.Khademi,Estimation of thermal conductivity of pure gases by using artificial neural networks,Int.J.Therm.Sci.48(2009)1094–1101.

[40]R.Boozarjomehri,F.Abdolahi,M.A.Moosavian,Characterization of basic properties for pure substances and petroleum fractions by neural network,Fluid Phase Equilib.231(2005)188–196.

[41]A.Z.Hezave,M.Lashkarbolooki,S.Raeissi,Using artificial neural network to predict the ternary electrical conductivity of ionic liquid systems,Fluid Phase Equilib.314(2012)128–133.

[42]H.Watanabe,H.Kato,Thermal conductivity and thermal diffusivity of twenty-nine liquids:alkenes,cyclic(alkanes,alkenes,alkadienes,aromatics),and deuterated hydrocarbons,J.Chem.Eng.Data49(2004)809–825.

[43]H.Watanabe,Accurate measurement of the thermal conductivity and thermal diffusivity of toluene andn-heptane,Int.J.Thermophys.18(1997)313–325.

[44]H.Watanabe,D.J.Seong,The thermal conductivity and thermal diffusivity of liquidn-alkanes:CnH2n+2(n=5 to 10)and toluene,Int.J.Thermophys.23(2002)337–356.

[45]H.Watanabe,Thermal conductivity and thermal diffusivity of sixteen isomers of alkanes:CnH2n+2(n=6 to 8),J.Chem.Eng.Data48(2003)124–136.

[46]M.Lashkarbolooki,B.Vaferi,A.Shariati,A.Z.Hezave,Investigating vapor–liquid equilibria of binary mixtures containing supercritical or near-critical carbon dioxide and a cyclic compound using cascade neural network,FluidPhaseEquilib.343(2013)24–29.

[47]http://www.cs.stir.ac.uk/～lss/NNIntro/InvSlides.html.

[48]M.Lashkarbolooki,B.Vaferi,D.Mowla,Using artificial neural network to predict the pressure drop in a rotating packed bed,Sep.Sci.Technol.47(2012)2450–2459.

[49]C.M.Rodenbush,D.S.Viswanath,F.H.Fu-hung Hsieh,A group contribution method for the prediction of thermal conductivity of liquids and its application to the Prandtl number for vegetable oils,Ind.Eng.Chem.Res.38(1999)4513–4519.

[50]M.R.Riazi,G.A.Enezi,S.Soleimani,Application of the one-third rule in hydrocarbon and crude oil systems,Chem.Eng.Commun.176(2007)175–193.

[51]A.Vasquez,J.G.Briano,Thermal conductivity of hydrocarbon mixtures:a perturbation approach,Ind.Eng.Chem.Res.32(1993)194–199.

[52]V.Pachaiyappan,S.H.Ibrahim,N.R.Kuloor,Chem.Eng.74(4)(1967)150.

[53]R.Mohammad,M.R.Riazi,A.Faghri,Thermal conductivity of liquid and vapor hydrocarbon systems:pentanes and heavier at low pressures,Ind.Eng.Chem.Process.Des.Dev.24(1985)398–401.