固定鸭舵双环PID制动控制算法

黄 伟，高 敏，宋卫东，王 毅

(解放军军械工程学院，河北 石家庄 050003)

固定鸭舵双环PID制动控制算法

黄 伟，高 敏，宋卫东，王 毅

(解放军军械工程学院，河北 石家庄 050003)

针对现有固定鸭舵制动控制算法不能及时准确制动的问题，提出了位置-速度双环PID制动控制算法。该算法包括位置和速度双环，位置环控制器根据目标滚转角和角位置反馈得到参考角速度，速度环控制器根据参考角速度与角速度反馈输出PWM波占空比值。仿真结果表明，该算法能够满足制动控制的技术指标要求，且在引入各项误差的情况下仍能保持稳定，具备一定的抗干扰能力，符合固定鸭舵制动控制的需求。

固定鸭舵；制动控制；双环PID；力矩计算

0 引言

固定鸭舵式二维弹道修正组件能够有效减小炮射弹药落点偏差，提高常规弹丸命中精度。固定鸭舵包含一对减旋舵和一对修正舵：减旋舵产生气动导转力矩，驱动固定鸭舵相对弹体低速反旋；修正舵提供弹道修正的气动力。无修正控制时，导转力矩驱动固定鸭舵相对弹体反向旋转；修正弹道时，通过制动控制使修正舵停止在某一滚转角，进而改变弹体合力方向，从而实现弹道修正。因此，制动控制算法的性能直接影响弹道修正的精度。

最早描述固定鸭舵式二维弹道修正组件的专利文献[1]中，并未提及固定鸭舵的制动控制细节。相关外文文献[2-3]对鸭舵的制动控制也未详细描述。高铭泽等[4]研究了双闭环控制算法，但未对轴承摩擦力矩进行深入研究，而打靶试验证明飞行过程中复杂环境下摩擦力矩不可忽略，郝永平等[5]也得出了摩擦力矩会影响控制效率的结论。杨恺华等[6]研究了模糊控制算法，该算法控制误差小且具备一定的抗干扰能力，但制动时间过长，不满足工程实际的需求。本文针对上述问题，提出一种固定鸭舵双环PID控制算法。

1 固定鸭舵的受力分析

弹丸发射后高速飞离炮口，一对差动舵产生导转力矩，驱动固定鸭舵克服摩擦力矩和极阻尼力矩相对弹体反旋(尾部视角下，弹体右旋，固定鸭舵左旋)。固定鸭舵制动时，永磁电机产生电磁力矩，控制固定鸭舵停在目标滚转角位置。固定鸭舵还受到沿弹轴方向力的作用，但本文研究固定鸭舵的制动，只涉及弹轴方向力矩，故不加考虑。

由于固定鸭舵转速较低，径向尺寸较小，极阻尼力矩很小，本文忽略其对固定鸭舵的作用。基于以上分析，固定鸭舵在制动过程中只受到导转力矩、摩擦力矩和电磁力矩作用。

1.1 空气导转力矩

来流作用于一对减旋舵产生垂直弹轴的作用力，对弹轴取矩形成空气导转力矩。根据空气动力学知识，该力矩是飞行马赫数Ma，鸭舵攻角α，空气密度ρ，舵片面积Sd等的函数，表达式如下：

Md=f(Ma,α,ρ,Sd)

(1)

通过风洞试验可以较快速地得到不同马赫数和攻角条件下的导转力矩数值，如图1所示。实际飞行试验中，可根据装订的理想弹道全弹道飞行速度和攻角变化，查表得到任意时刻固定鸭舵导转力矩值。

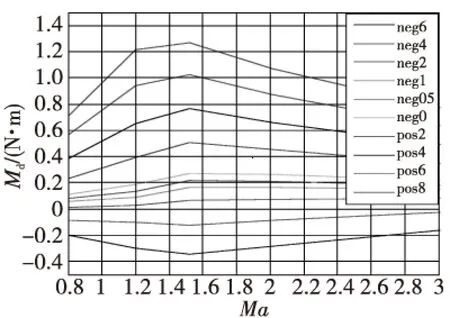
图1 空气导转力矩随马赫数和攻角变化曲线Fig.1 Curves of Md in different Ma and angle of attack

1.2 摩擦力矩

摩擦力矩的主要来源是轴承，修正组件的头部和尾部通过两个滚珠轴承来连接，一方面可以实现组件头部的减旋，另一方面可以保证头部和尾部同轴旋转。轴承内环与头部固连，外环与尾部固连，内外环之间有加保持架的圆珠滚子。弹丸飞行过程中，圆珠滚子与轴承之间的摩擦作用在头部，形成摩擦力矩。滚动轴承摩擦力矩的计算公式[7]如下：

(2)

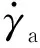
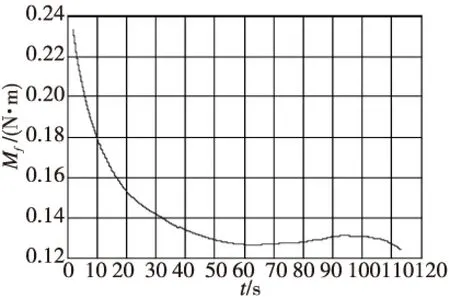
图2 全弹道摩擦力矩曲线Fig.2 Curve of Mf in the whole trajectory

1.3 电磁力矩

电磁力矩来源于绕组电流产生的磁场与永磁体磁场的相互作用，其大小由永磁体磁通密度Bm和永磁体极弧幅值β、电机气隙直径D、叠片长度L和每相绕组匝数Ns、绕组电流幅值Im和转矩角δ决定，如下式：

T=3DLBm(sinβ)NsImsinδ/2

(3)

式(3)中，永磁体磁通密度Bm和永磁体极弧幅值β、电机气隙直径D、叠片长度L和每相绕组匝数Ns等常数在电机的设计环节确定。电机的控制策略选择恒转矩角控制(δ=90°)，则电磁力矩仅与电流成正比关系，通过调节绕组电流幅值即可调节电磁力矩大小。

本文采用斩波调压调节绕组电流幅值[9]的方法来控制电磁力矩大小。由占空比的定义和欧姆定律，并结合式(3)可得，电磁力矩与占空比是线性关系。即：

Te=Tmaxα

(4)

式(4)中，Tmax是电磁力矩最大值，α为PWM波的占空比，取值范围为[0,1]。制动控制时，制动控制算法根据目标滚转角以及角位置和角速度反馈，计算得到对应的占空比值α，占空比为α的PWM波驱动电机输出Te，使反旋的固定鸭舵减速并制动。

2 双环PID制动控制算法

固定鸭舵的制动过程，是受控电磁力矩、空气导转力矩和摩擦力矩共同作用下，固定鸭舵相对地面静止坐标系减速停止的过程。制动过程中，控制算法根据固定鸭舵实时的滚转角速度和角位置信息，计算得到对应的PWM占空比值，输出给永磁电机驱动电路，控制电机作动实现鸭舵制动。鸭舵制动的技术要求为调节时间不大于1 s，稳态误差不大于5°。

2.1 制动控制算法的结构

固定鸭舵双环PID制动控制算法的结构如图3所示。以目标滚转角与角位置反馈值的差值作为位置环PID控制器的输入，输出一个参考角速度；以参考角速度与角速度反馈值的差值作为速度环PID控制器的输入，输出PWM占空比值。固定鸭舵转速稳定是快速准确制动的前提条件，也是保证不执行制动时，修正力沿周向均匀分布、不引入额外弹道偏差的有效措施，因此在位置环控制器之后加入一个调速/制动模式切换模块。

图3 控制系统结构框图Fig.3 Structure of control system

要迅速准确地制动，固定鸭舵转速不能太低，以免响应时间过长；固定鸭舵的转速也不能过高，以免超调量过大甚至失控。经过不同初始转速下制动仿真实验发现，固定鸭舵平衡转速为10 r/s左右时制动效果最佳。因此，提出一种先稳定转速，再执行制动的控制策略，即在实际开始制动控制之前，先控制固定鸭舵的转速稳定在10 r/s，然后再进行制动。

鸭舵角位置反馈值φ由地磁组件测得，角速度反馈值ω由陀螺组件测得，目标滚转角θ由弹载计算机按照修正控制算法计算得到。

2.2 制动控制算法设计

速度控制要求响应速度快，具备一定的抗干扰性能，故将速度环校正为典型的Ⅱ型系统；位置控制要求跟随性能好，稳态精度高，将位置环校正为Ⅰ型系统[10]。根据上述原则确定PID控制器的形式和参数。

2.2.1 速度环控制器形式及参数

速度环包含PWM逆变环节、电磁力矩生成环节、固定鸭舵速度环节和速度反馈环节，各环节传递函数如下：

(5)

式(5)中各参数的含义及数值详列于表1中。

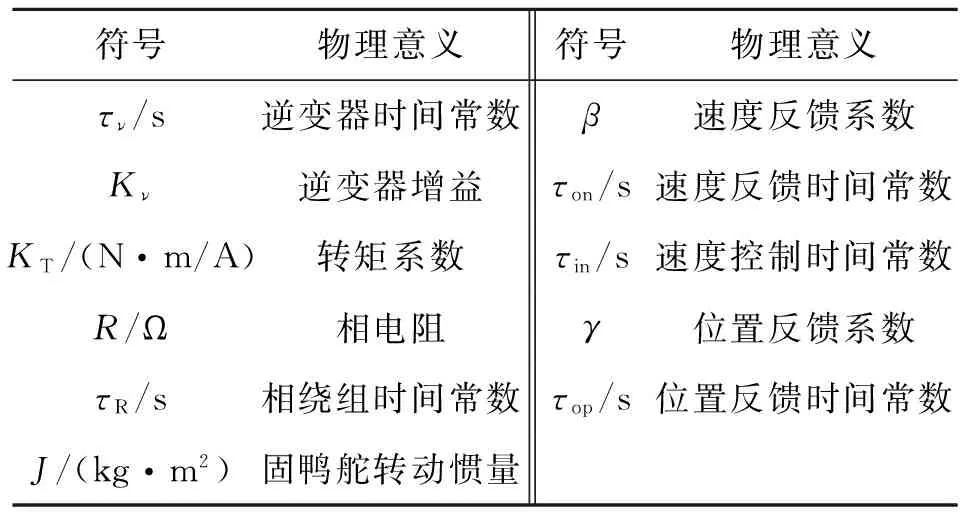
表1 变量对照表

得到速度PID控制对象的传递函数为：

(6)

两个时间常数较小且相近的惯性环节串联，可等效为时间常数为两时间常数相加的新惯性环节。由于τR和τν均较小且相近，可取τon=τR+τν，经两次小惯性环节等效，速度环控制对象的传递函数可简化为：

(7)

其中，小惯性环节等效的条件分别为：

(8)

由于速度环控制对象有一个积分环节和一个惯性环节，为了速度控制后没有静差，速度控制器必须有一个积分环节，而为了使速度环响应迅速，去除微分环节，则速度环控制器的形式选择PI控制器。速度环开环传递函数为：

(9)

按照典型Ⅱ型系统分析方法，定义一个中频宽度h=5，根据式(10)可以计算得到τin、Kpn。

(10)

以上常数确定后，检验小惯性环节的等效条件式，不等式(8)成立，表明小惯性环节等效处理可行。

2.2.2 位置环控制器形式及参数

速度环校正之后的位置环包含速度闭环、速度积分环节和位置反馈环节。则位置环控制对象传递函数为：

(11)带入各参数的值进行计算，由于τ1n、τ2n大小相近，选定τop≈(τ1n+τ2n)/2，按照小惯性环节等效理论，三个小时间常数惯性环节可由时间常数为τp=τ1n+τ2n+τop的惯性环节，则位置环控制对象传递函数简化为：

(12)

小惯性环节的等效条件是：

(13)

位置环要求响应速度快、无超调，因而校正为Ⅰ型系统，故位置调节器选用P控制器。设位置超调量小于5%，可由γKppτp=0.5计算比例系数Kpp。确定系数后检验小惯性环节的等效条件，不等式(13)成立，表明小惯性环节等效处理可行。

3 仿真实验结果及分析

按照上述控制算法结构和参数整定结果，基于MATLAB/ SIMULINK平台建立系统仿真模型，如图4所示。

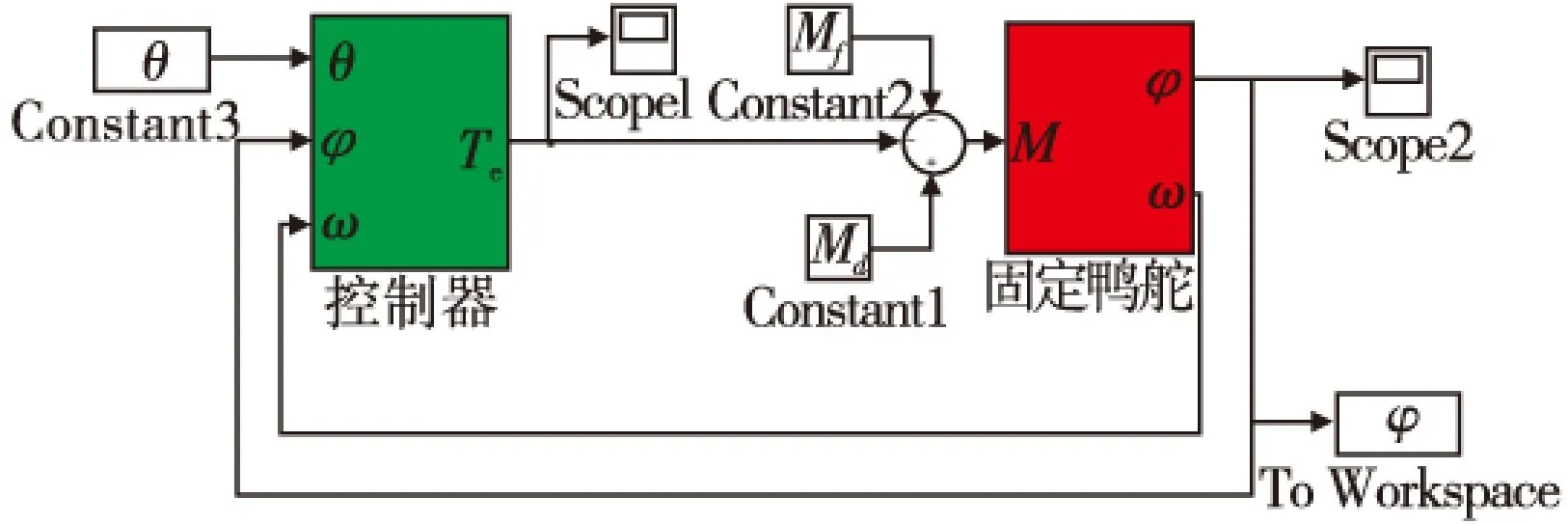
图4 系统仿真模型Fig.4 System simulation model

(14)

(15)

(16)

固定鸭舵模块按照其动力学关系式(14)和运动学关系式(15)、式(16)编制，式中的α，ω，φ分别表示固定鸭舵的滚转角加速度、滚转角速度和滚转角位置，ω0，φ0分别表示滚转角速度和角位置初值；控制器部分按照位置-速度双环PID算法编制。

仿真以炮弹发射后20 s时刻为计时零点，给定控制角度90°，180°，270°和360°(0°)，给定固定鸭舵滚转角速度初值ω0为20 r/s，滚转角位置初值φ0为0°。首先进行转速稳定控制，然后在t=1 s时执行制动，得到结果如图5所示。图中标出了固定鸭舵在受控状态下达到目标滚转角±5°误差带的时间，作为系统响应速度的参考。

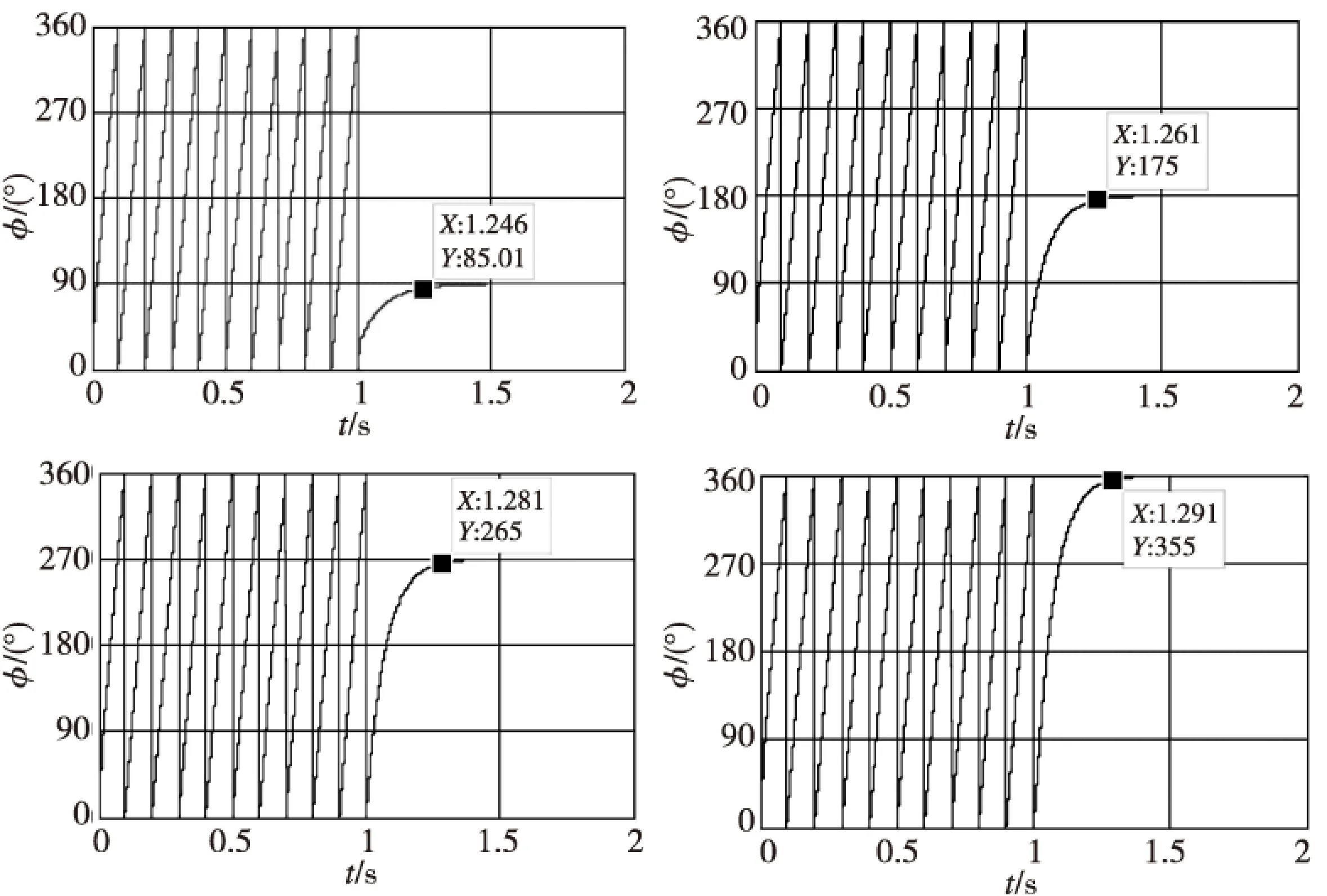
图5 固定鸭舵制动曲线Fig.5 Curves of fixed-canard braking

从图5中可以看出，仿真开始后固定鸭舵的转速控制响应迅速，且转速能够迅速稳定在10 r/s的转速。在稳定转速的前提下，制动控制响应速度快、无超调，在0.3 s内达到制动控制允许的误差范围内，稳态误差不超过0.5°。控制角度为90°，180°，270°和360°(0°)的制动曲线比较，可知制动系统的响应速度和稳态误差，并不受目标滚转角位置影响，因此对于任意目标角位置该算法都是稳定的。以上分析可知，本文设计的制动控制算法满足制动控制的全部技术指标要求。

弹丸实际飞行环境条件复杂，气象条件和硬件设备参数并非恒定的，制动过程中容易受到各种干扰的影响。其中，受空气条件等影响，导转力矩的计算值与实际值存在误差，地磁组件输出的滚转角位置和滚转角速度也会受地磁传感器精度和复杂电磁环境的干扰。为了确保制动控制算法实际可用，分别在理想条件下添加各项干扰，对比分析不同干扰条件下制动控制算法是否仍然有效。

图6为在180°控制角仿真中，分别添加导转力矩的计算误差(t=2 s时添加50%阶跃力矩误差信号)、滚转角位置测量误差(均值为5°,方差为1°2的随机误差)、滚转角速度测量误差(均值为0.1 r/s,方差为0.01 r2/s2的随机误差)和综合误差的制动控制曲线。从图中可以看出，在各项误差条件下，控制算法仍然稳定可用，最大角位置误差约为5°，仍然能够满足制动控制的技术指标要求。

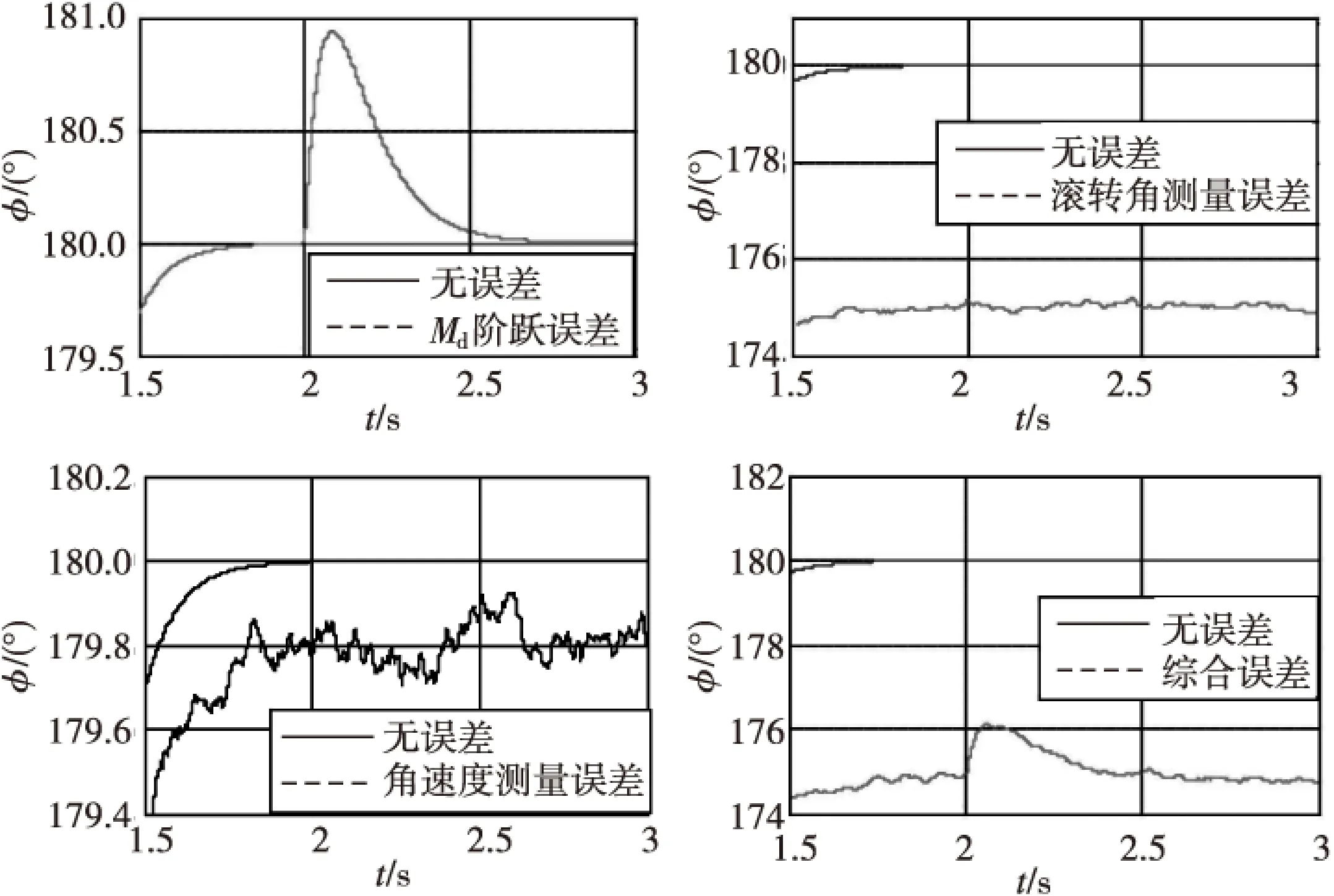
图6 加不同误差的制动曲线(局部放大)Fig.6 Curves of braking with different error

4 结论

本文提出了固定鸭舵双环PID制动控制算法。该算法包括位置环和速度环，位置环控制器根据目标滚转角和角位置反馈得到参考角速度，速度环控制器根据参考角速度与角速度反馈输出PWM波占空比值。本文首先对固定鸭舵所受空气导转力矩、摩擦力矩和电磁力矩进行了分析；然后根据先稳定转速、再执行制动的控制策略设计了位置-速度双环PID控制算法。基于Matlab的仿真实验结果证明了控制算法能够满足制动控制的技术指标要求，且在引入各项误差的情况下仍能保持稳定，具备一定的抗干扰能力。速度环是典型的Ⅱ型系统，在导转力矩突变和角速度测量误差的条件下能迅速消除干扰影响、稳态误差小；但由于位置环控制器仅由比例环节构成，导致位置环的滚转角位置测量误差对稳态误差影响较大。实际应用中采用的地磁传感器测量滚转角位置，误差最大能达到±5°左右，拟在后续研究中继续对算法改进，以期能够改善位置环的抗干扰性能。

[1]ClancyJA,BybeeTD,FridrihW.FixedCanard2-DGuidanceofArtilleryProjectile：US6981672B2[P].2006-1-3.

[2]FresconiF,CooperG,CelminsI,etal.Flightmechanicsofanovelguidedspin-stabilizedprojectileconcept[J].JournalofAerospaceEngineering, 2012, 226(3): 327-340.

[3]HeodoulisS,GassmannV,WernertP,etal.Guidanceandcontroldesignforaclassofspin-stabilizedin-controlledprojectiles[J].JournalofGuidance,Control,andDynamics, 2013, 36(2): 517-531.

[4]高铭泽,施坤林,霍鹏飞,等.引信滚转角双闭环控制算法[J].探测与控制学报, 2013, 35(3): 17-20.

[5]郝永平,郭煜洋,张嘉易,等.轴承摩擦力矩对智能引信控制效率的影响[J].弹箭与制导学报, 2014, 34(4): 69-77.

[6]杨恺华,祁克玉,王芹.基于模糊控制的二维弹道修正引信滚转角控制算法[J].探测与控制学报, 2015, 37(2): 19-23.

[7]张卫华.滚动轴承摩擦力矩的计算分析[J].轴承, 2008(7): 1-3.

[8]刘泽九.滚动轴承应用手册[M].北京: 机械工业出版社, 1996: 423-425.

[9]张进超,王玲,郝永平,等.某种永磁同步发电机直接转矩控制系统设计[J].机械与电子, 2015, (7): 34-37.

[10]袁海宵.永磁无刷直流电动机位置伺服系统的研究[D].南京: 南京航空航天大学, 2011.

版 权 声 明

凡稿件被本刊录用,即视为作者同意将该论文的复制权、发行权、信息网络传播权、翻译权、汇编权等权利在全世界范围内转让给本刊。本刊已许可中文科技期刊数据库、万方数据数字化期刊群、中国知网(中国学术期刊(光盘版)电子杂志社)和超星域出版系统在其各自的系列数据库产品中以数字化方式复制、汇编、发行及在信息网络传播本刊全文。作者著作权使用费和稿酬一并支付(即包括印刷版、光盘版和网络版各种使用方式的报酬)。如作者对本声明持有异议,请在投稿时说明。

本刊编辑部

Double-loop PID Algorithm for Fixed Canard Braking Control

HUANG Wei, GAO Min, SONG Weidong, WANG Yi

(Ordnance Engineering College of PLA, Shijiazhuang 050003, China)

In order to solve the problem that the existing fixed canard braking control algorithm cannot meet the need of celerity and accuracy, a position-speed double-loop PID braking control algorithm was proposed in this paper. The algorithm consists of a position loop which output a reference speed depending on the target angle and feedback angle and a speed loop which output duty cycle according to the reference speed and the feedback speed. The simulation results showed that the control algorithm satisfied all technical index and had capacity of resisting disturbance, which made the algorithm stable in different errors condition.

fixed canard; braking control; double-loop PID; torque calculation

2016-11-13

武器装备预研基金项目资助(9140A05040114JB34015)

黄伟(1991—)，男，土家族，湖北恩施人，硕士研究生，研究方向：弹箭信息化与智能化技术。E-mail:buaahuangwei@126.com。

TJ439

A

1008-1194(2017)02-0054-05