离心和火药自毁引信自毁时间分布特性
2017-05-25王雨时黄军华张志彪
张 元,王雨时,黄军华,张志彪,闻 泉
(1.南京理工大学机械工程学院,江苏 南京210094;2.江西 9304厂,江西 九江332006)
离心和火药自毁引信自毁时间分布特性
张 元1,王雨时1,黄军华2,张志彪1,闻 泉1
(1.南京理工大学机械工程学院,江苏 南京210094;2.江西 9304厂,江西 九江332006)
针对火炮引信自毁时间散布和精度控制问题,提出了利用引信产品验收靶试数据和数理统计手段拟合其分布规律并利用得到的结果计算引信自毁时间的相关参数的方法。该方法对5型引信自毁时间数据针对17种常用分布类型进行检验,拟合结果表明,除A型引信自毁时间服从正态分布外,其余4种均不服从,离心自毁的A型引信和C型引信自毁时间均服从对数正态分布、广义极值分布、Birnbaum-Saunders分布和反高斯分布,火药自毁的B型引信、D型引信和E型引信自毁时间共同服从Burr分布,其中D型引信和E型引信自毁时间均服从t Location-Scale分布,验证结果表明,利用得到的结果计算引信自毁时间的相关参数来判断是否满足指标是可行的。
引信;自毁时间;数理统计;分布特性
0 引言
因性能和结构尺寸要求所限,小口径火炮引信自毁主要采用火药自毁和离心自毁。目前,大部分引信自毁机构都采用离心自毁方式[1],但仍保留有火药自毁方式。离心自毁机构是利用弹丸在外弹道飞行过程中转速即离心力的衰减规律来控制自毁的引信辅助机构[2],具有长期贮存性好、占用空间小、易与触发发火机构结合设计、在一定范围内能自动适应弹道变化等优点[3],但也存在自毁时间散布大的缺点。对于造成自毁时间散布的原因,目前已有较多的研究[4-5]。但对于如何控制引信自毁时间的散布和精度,目前仅见文献[6]应用可靠性理论,推断引信自毁时间的分布规律来分析自毁时间的相关参数,从而掌握自毁机构的主要参数设计来达到控制引信自毁时间的散布和精度的目的。但文献[6]只分析了一种型号的引信自毁时间,且只针对钢珠式离心自毁机构,其推断出的分布类型只有对数正态分布,未确定引信自毁时间是否服从其他分布。针对此问题,本文利用数理统计方法和Matlab软件对离心和火药自毁的5型引信生产交验靶试自毁时间数据针对17种常用分布类型进行检验,分析其服从的分布规律,并利用得到的结果计算引信自毁时间的相关参数。
1 K-S检验
在数理统计中,常用的分布拟合检验方法有χ2检验和K-S检验,一般认为K-S检验的检验效果较好。K-S检验法全称为柯尔莫哥洛夫-斯米尔诺夫(Kolmogorov-Smirnov)检验法。该方法不是分区间检验样本与理论分布之间的偏差,而是对每一个点都检验它们之间的偏差,因此,K-S检验法比较精确[7]。
K-S检验法在Matlab软件中有专门的函数,可以很方便地通过软件来检验数据在显著水平α下是否服从某种分布规律,其具体命令如下:
[H,P,KSSTAT,CV] = kstest(X,cdf,α)式中,X为样本数据,在本文中即为引信自毁时间数据,cdf为求目标分布规律累积故障分布曲线的函数,KSSTAT 为测试统计量的值,CV为是否接受假设的临界值,H为判定是否拒绝原假设的指标。若H=0则不能拒绝原假设,即样本与分布规律不存在明显差异,H=1则一定可以拒绝原假设,即样本与分布规律存在明显差异。P值为原假设成立的概率,P值越大,表明样本越服从这种分布规律。一般情况下,当P值大于0.05时就可以认为原假设成立,即样本服从目标分布规律。因此利用P值,就可确定引信自毁时间是否符合分布规律,并通过比较不同分布规律的P值确定自毁时间服从的最佳分布类型。
2 分布曲线拟合
自生产厂家处共获得5种(分记为A型、B型、C型、D型和E型)引信型号产品生产交验靶场试验自毁时间数据,各型号引信具体技术状态如表1所示。
从表1可知,A型和C型的引信自毁时间是在不同的检验环境下测得,但经分析发现震动、水平跌落、头向下跌落和常态等勤务环境对引信离心球自毁时间性能无显著影响[8],在分析引信离心球自毁时间分布规律时可不考虑其影响。将自毁时间样本数据导入Matlab工作空间,得到图1所示数据频数直方图。

表1 各型引信自毁时间关键参数
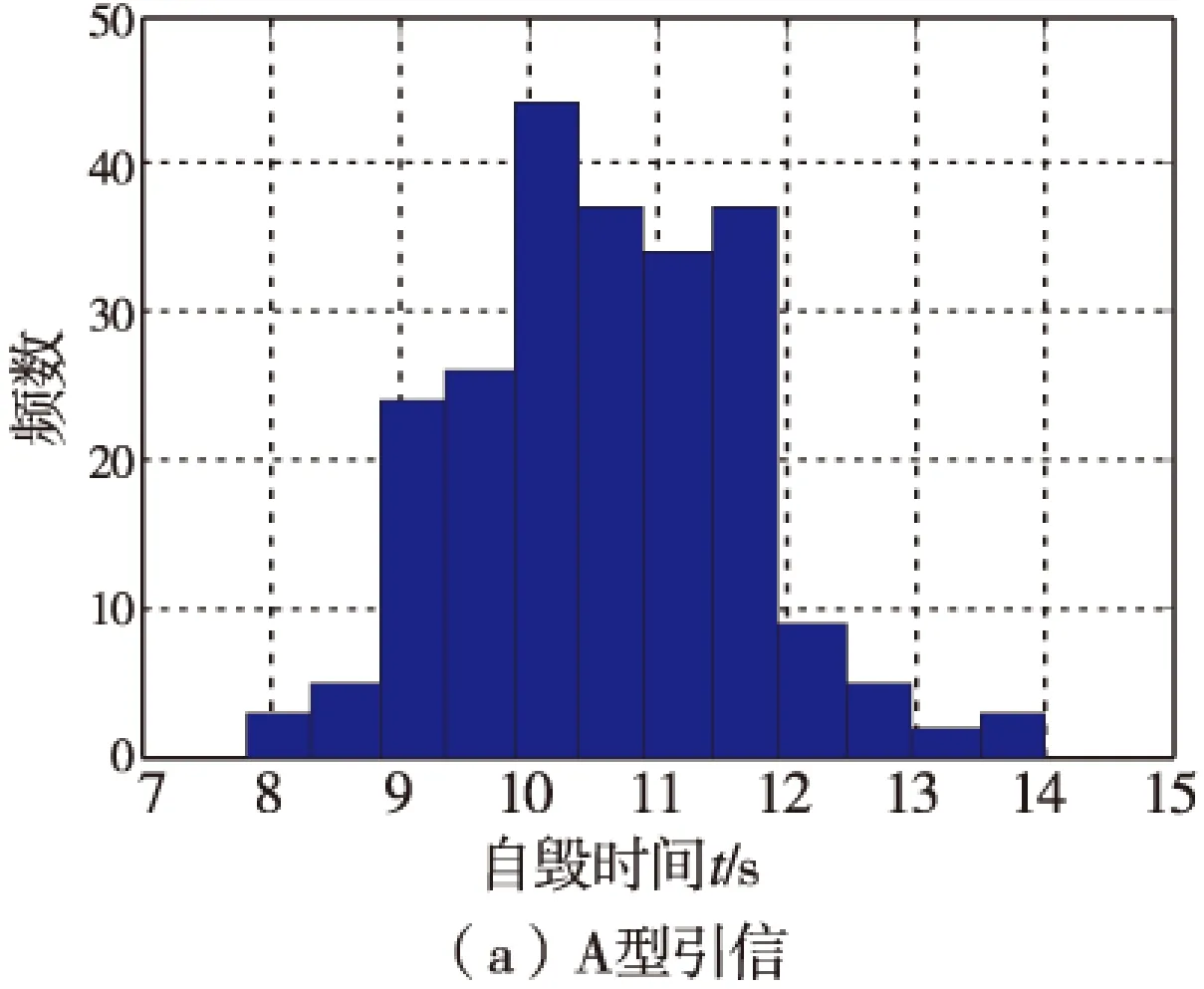

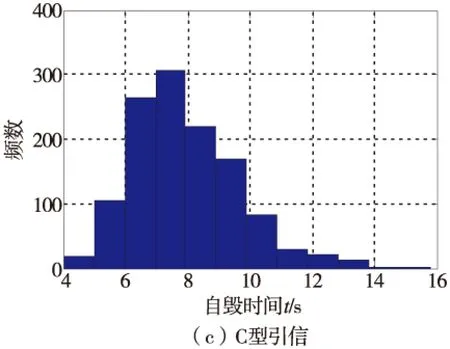
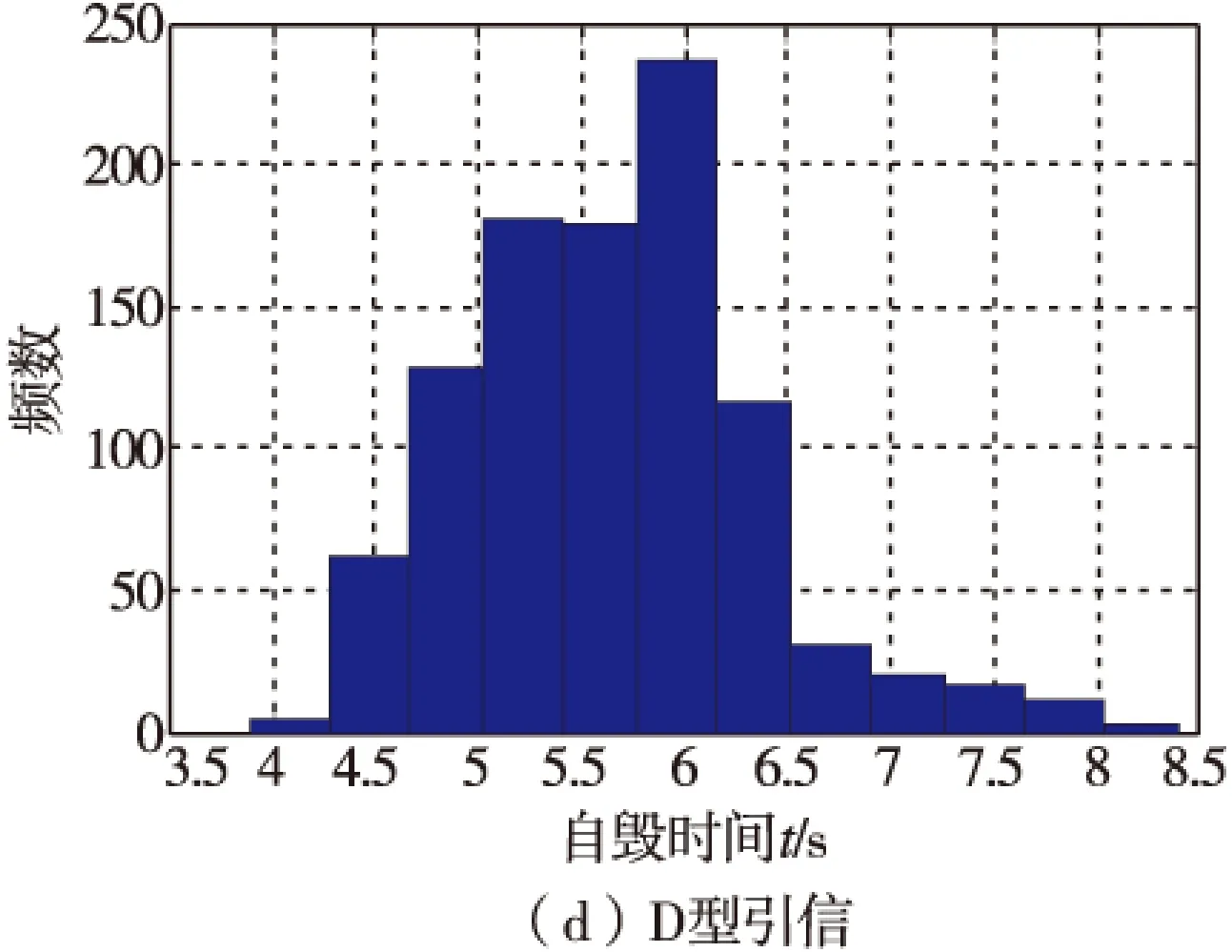

图1 A—E型引信自毁时间数据频数直方图Fig.1 The frequency histogram of A—E type fuze self-destroying time
根据绘出的自毁时间频数直方图,可假设其服从某一分布,如正态分布、对数正态分布等,然后对假设分布进行参数估计和假设检验。传统数理统计和概率计算的方法工作量很大,且容易遗漏分布类型。为简化计算,且确保不遗漏分布类型,本文采用Matlab分布拟合工具Diftool(Distrbution-Fitting-Tool)对各种可能的分布进行曲线拟合。
在Matlab分布拟合工具Diftool中共有17种分布类型,通过绘制拟合曲线并以累积概率曲线显示,从图形可直观地看出分布函数的拟合程度,从而排除偏离较大的分布类型[9]。图2为A型引信自毁时间的几种分布的拟合曲线,从中可看出指数分布与原数据偏离较大,因此可以剔除。通过该方法共剔除指数分布、Rayleigh分布和GeneralizedPareto分布3种分布类型。

图2 A型引信自毁时间累积概率曲线拟合图Fig.2 Cumulative probability curve fitting of A type fuze self-destroying time
经过筛选,共有正态分布、Nakagami-m分布等14种分布的拟合曲线与A型引信原始数据曲线基本吻合。要进一步确定引信自毁时间数据是否服从这些分布,需要进行参数估计和假设检验,参数估计值可通过Diftool分布拟合工具得出结果,A型引信自毁时间分布规律参数估计值如表2所示。
3 分布拟合检验
在显著水平α=0.05下,对表2中的17种分布类型进行K-S检验,并以原假设成立概率P的大小从大到小排序,结果如表3所示。
一般情况下,当P值大于0.05时,就可认为样本数据服从此分布规律。观察表3知,不同型号的引信的自毁时间服从的分布规律不同,对于A型引信,除极值分布、Rayleigh分布、Generalized Pareto分布和指数分布外,其他分布类型的P值都大于0.05,且Nakagami-m分布的P值最大,正态分布次之,因此可认定A型引信自毁时间服从这13种分布类型,不服从极值分布、Rayleigh分布、Generalized Pareto分布和指数分布这4种分布,服从的分布类型中包括文献[6]所得到的对数正态分布。对于B型引信,除广义极值分布和Burr分布,其他分布类型的P值都小于0.05,因此B型引信自毁时间服从广义极值分布和Burr分布,不服从其他分布类型,对于C型、D型和E型引信,所有分布类型的P值都小于0.05,即C型、D型和E型引信自毁时间不服从列举的所有分布规律。结合表1和表3,发现拟合结果较好的A型和B型引信的自毁时间数据量较少,而拟合结果较差的C型、D型和E型引信数据量较多,由此推测当自毁时间数据量较少时,拟合效果更好,而自毁时间数据较多时,拟合效果变差,为验证此结论,将拟合效果较差的C型、D型和E型引信减少数据量重新进行拟合,拟合结果如表4所示。
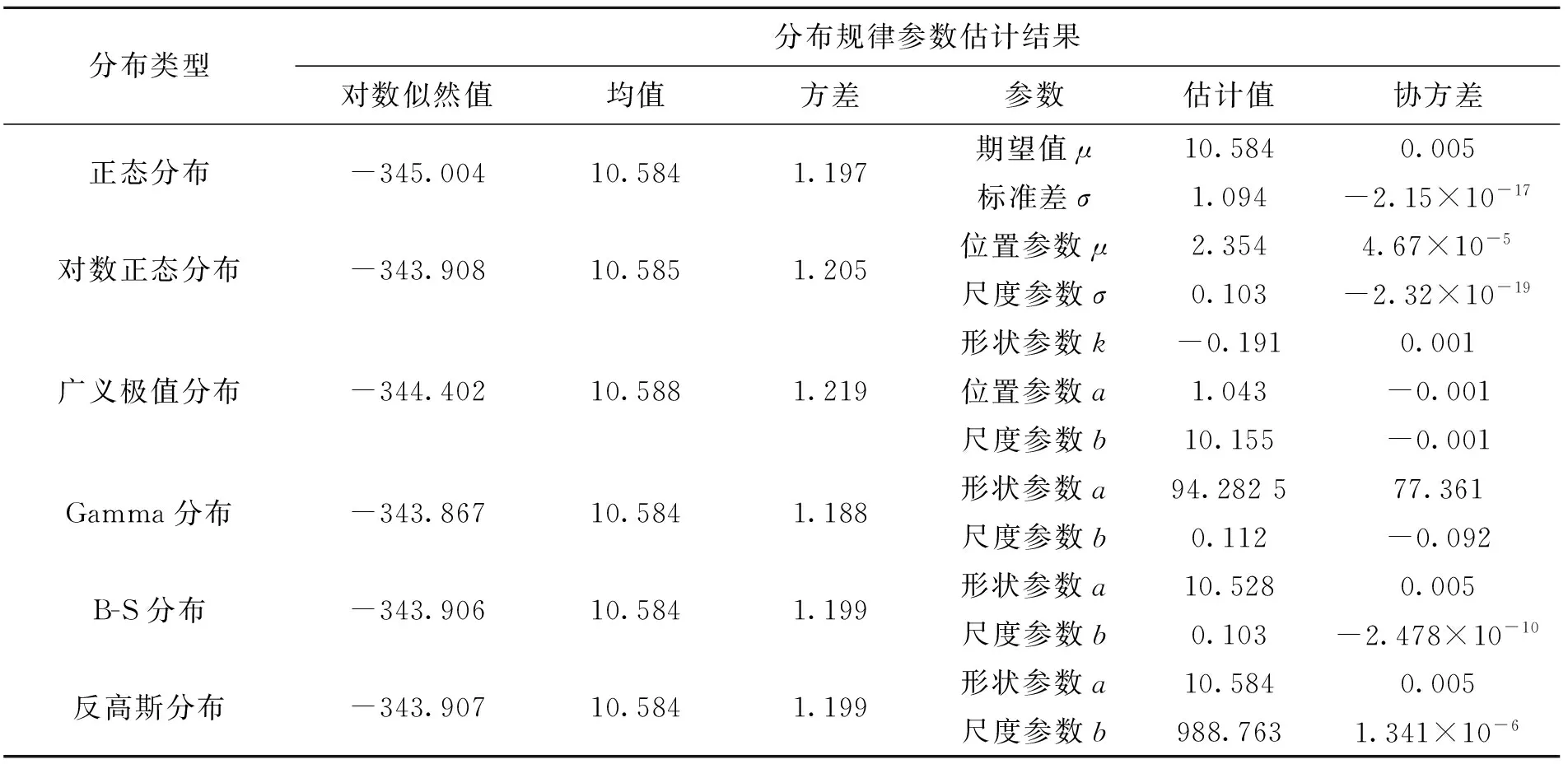
表2 A型引信自毁时间分布规律参数估计值
(续表)
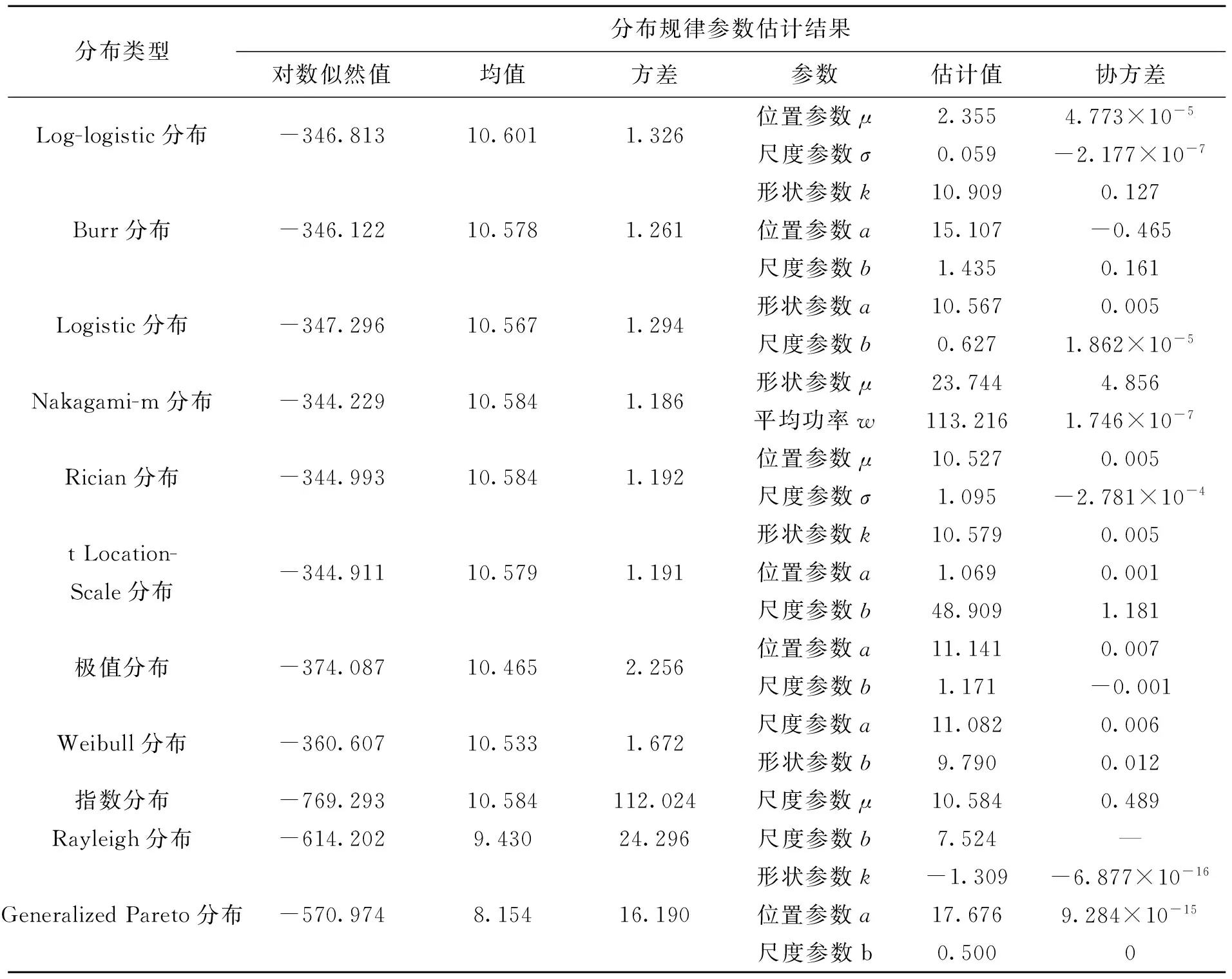
分布类型分布规律参数估计结果对数似然值均值方差参数估计值协方差Log-logistic分布-346.81310.6011.326位置参数μ2.3554.773×10-5尺度参数σ0.059-2.177×10-7Burr分布-346.12210.5781.261形状参数k10.9090.127位置参数a15.107-0.465尺度参数b1.4350.161Logistic分布-347.29610.5671.294形状参数a10.5670.005尺度参数b0.6271.862×10-5Nakagami-m分布-344.22910.5841.186形状参数μ23.7444.856平均功率w113.2161.746×10-7Rician分布-344.99310.5841.192位置参数μ10.5270.005尺度参数σ1.095-2.781×10-4tLocation-Scale分布-344.91110.5791.191形状参数k10.5790.005位置参数a1.0690.001尺度参数b48.9091.181极值分布-374.08710.4652.256位置参数a11.1410.007尺度参数b1.171-0.001Weibull分布-360.60710.5331.672尺度参数a11.0820.006形状参数b9.7900.012指数分布-769.29310.584112.024尺度参数μ10.5840.489Rayleigh分布-614.2029.43024.296尺度参数b7.524—GeneralizedPareto分布-570.9748.15416.190形状参数k-1.309-6.877×10-16位置参数a17.6769.284×10-15尺度参数b0.5000
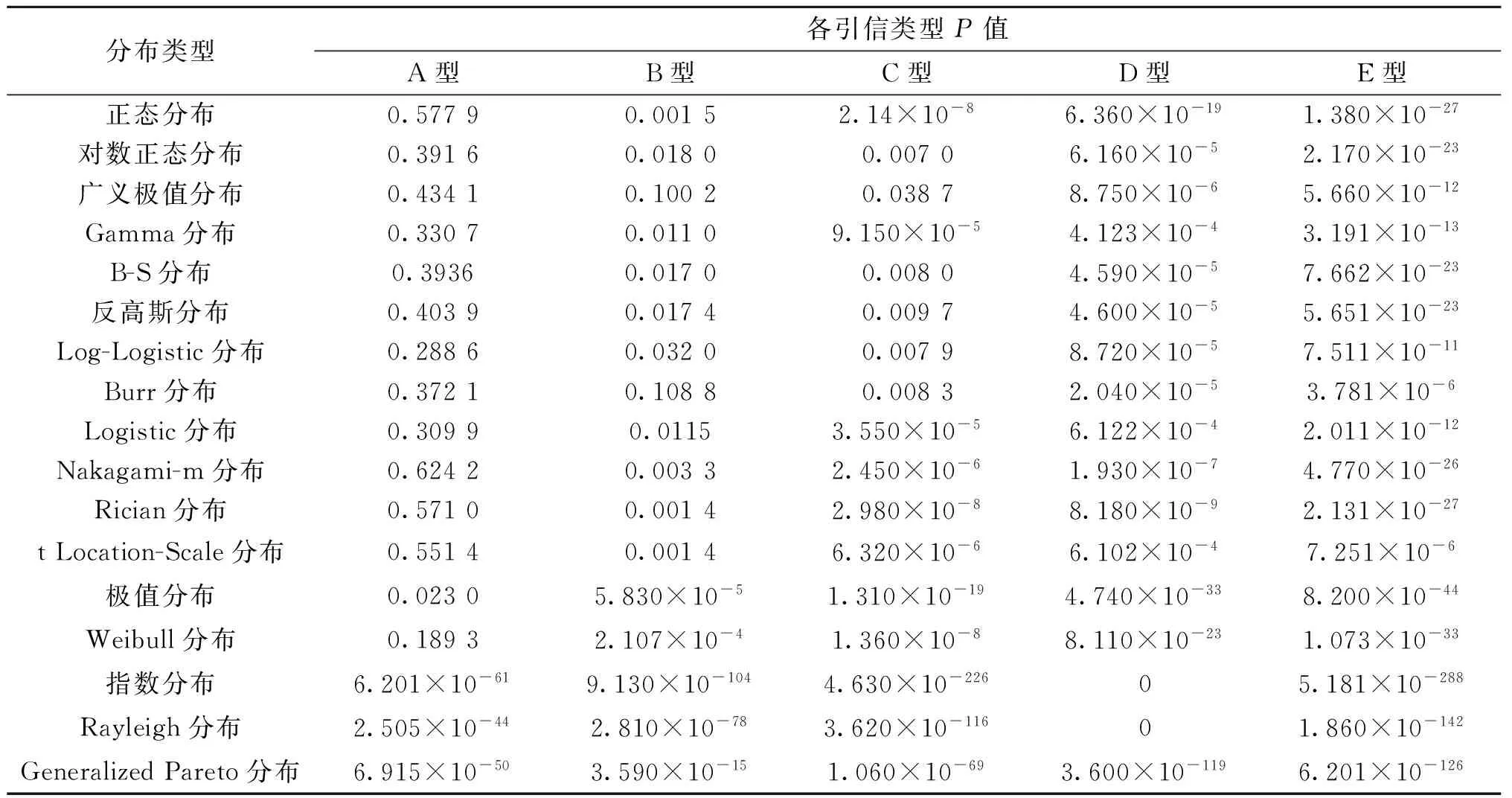
表3 各分布类型拟合程度对比

表4 C型、D型和E型引信各分布类型拟合程度
表4中的C型引信的拟合结果为其自毁时间数据量降为600后的结果,从拟合结果来看,C型引信自毁时间服从对数正态分布和广义极值分布等4种分布类型,D型引信拟合结果为其自毁时间数据量降为80后的结果,此时D型引信自毁时间服从Log-Logistic分布和Burr分布等4种分布类型, E型引信拟合结果为其自毁时间数据量降为100后的结果,E型引信自毁时间服从Burr分布和t Location-Scale分布。对比表3和表4可知,除A型引信自毁时间服从正态分布外,其余型号均不服从;离心自毁的A型引信和C型引信自毁时间都服从对数正态分布和广义极值分布等4种分布类型;火药自毁的B型引信、D型引信和E型引信自毁时间都服从Burr分布,其中D型引信和E型引信自毁时间都服从t Location-Scale分布;随着自毁时间数据量的增加,自毁时间的散布规律出现了变化。
由表3可知,经过分布拟合检验得出,A型引信自毁时间满足正态分布和广义极值分布等13种分布,并更符合Nakagami-m分布。下面通过计算样本均值、方差、最大概率自毁时间和分布区间来验证分布类型的准确性。
从表5可以看出,根据Nakagami-m分布计算得到的A型引信自毁时间参数与样本实际情况吻合得较好。两者均值相对误差不超过0.1%,方差相对误差不超过1%,最大概率自毁时间基本吻合,在置信度99.74%下算得的最小值与最大值与样本实际分布区间基本吻合。因此,利用实验数据拟合分布规律,再通过得到的分布规律计算自毁时间的相关指标来判断其是否满足要求是可行的。

表5 Nakagami-m分布计算值与样本值对比
4 结论
本文提出了利用引信产品验收靶试数据和数理统计手段拟合其分布规律并利用得到的结果计算引信自毁时间的相关参数的方法。该方法对5型引信自毁时间数据针对17种常用分布类型进行检验,拟合结果表明自毁时间的数据量对结果有影响,数据量的增加会使自毁时间的分布特性出现变化。除A型引信自毁时间服从正态分布外,其余4种均不服从,离心自毁的A型引信和C型引信自毁时间均服从对数正态分布、广义极值分布、Birnbaum-Saunders分布和反高斯分布,火药自毁的B型引信、D型引信和E型引信自毁时间均服从Burr分布,其中D型引信和E型引信自毁时间均服从t Location-Scale分布,经过对A型引信自毁时间数据的验证,发现利用引信自毁时间测试数据拟合分布规律,再通过得到的分布规律计算自毁时间的相关指标来判断其是否满足要求是可行的。
[1]刘刚,王侠,丁锋.弹带飞边对引信离心自毁时间的影响[J].探测与控制学报,2008,30(6):60-65.
[2]纪永祥,李国芳,张景玲,等.引信自毁时间异常分析[J].探测与控制学报,2004,26(1):45-48.
[3]王雨时,陈志跃,王强.引信离心钢球自毁时间精度分析[J].探测与控制学报,2002,24(4):29-34.
[4]王雨时.引信离心自毁时间性能与设计指标分析[J].探测与控制学报,1999,21(1):52-59.
[5]王明辉.小口径引信钢球式离心自毁机构性能分析[D].南京:南京理工大学,2008.
[6]刘立先.小口径引信用钢球式离心自毁机构自毁时间分布可靠性分析[J].探测与控制学报,1994,(4): 55-62.
[7]兰波.基于K-S检验法的雪荷载统计分析[J].兰州理工大学学报,2012,38(1):115-119.
[8]黄军华,张元,王雨时,等.勤务环境对引信离心钢球自毁时间性能影响分析[J].兵器装备工程学报,2016(6):72-75.
[9]刘海波,江 健.基于MATLAB的某型挖掘机可靠性分布模型辨识[J].工程机械,2014,45(10):18-23.
Characteristics of Self-destroying Time Distribution of Artillery Fuze
ZHANG Yuan1, WANG Yushi1,HUANG Junhua2,ZHANG Zhibiao1,WEN Quan1
(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing,210094,China; 2.Jiangxi 9304 Company, Jiujiang 332006,China)
In order to analyze the distribution about small caliber fuze self-destroying time and to control its precision, a method that using production inspection data and mathematical statistics to fit its distribution law and further calculate the related index was proposed. Five types fuze self-destruction time were tested to see whether the data obey the 17 types of distribution by this method. It was found that the A type fuze obeyed normal distribution and the other 4 types did not. The self-destroying time of A type fuze and B type fuze which self-destructed by centrifugal ball self-destroying device obey log normal distribution and generalized extreme value distribution.The self-destroying time of B type fuze , D type fuze and E type fuze which self-destructed by gunpowder obeyed Burr distribution.The self-destroying time of D type fuze and E type fuze obeyed t Location-Scale distribution. By using test data of fuze self-destroying time which fitted distribution law to calculate the related index to judge whether it met the requirements was feasible.
fuze; self-destroying time; mathematical statistics; distribution characteristics
2016-10-09
张元(1992— ),男,湖南长沙人,硕士研究生,研究方向:引信技术。E-mail:144938657@qq.com。
TJ430
A
1008-1194(2017)02-0038-06
