基于贝叶斯推理的ANFIS电网发展水平评估

牛东晓，刘卫东，黄雅莉，孙可，刘鸿飞，吴晗

（1.华北电力大学经济与管理学院，北京 102206；2.国网浙江省电力公司经济技术研究院，浙江杭州 310000）

基于贝叶斯推理的ANFIS电网发展水平评估

牛东晓1，刘卫东2，黄雅莉1，孙可2，刘鸿飞1，吴晗1

（1.华北电力大学经济与管理学院，北京 102206；2.国网浙江省电力公司经济技术研究院，浙江杭州 310000）

电网发展水平评估是电网规划和建设的可靠前提和依据。首先，建立全面合理的电网发展水平评估指标体系；再根据贝叶斯推理的ANFIS建立电网评估模型；最后，利用实际样本进行模型训练和测试。算例结果显示模型的有效性。

电网评估；贝叶斯推理；自适应神经模糊推理系统

目前，受我国所处经济发展阶段的影响，作为公共基础设施的电力系统，其建设和发展仍然存在着较大的压力。准确、客观地认识电网发展状况，对电网的供电能力、供电可靠性等方面进行准确地评估，需要依靠电网发展水平评估技术。一项科学合理的电网发展水平评估技术，能够为电网的未来发展提供理论支持和决策依据，进而保证电网发展科学合理[1-2]。由此可见，电网发展水平评估研究对解决我国电力系统建设和发展中存在的问题意义深远[3]。

目前，国内已经有越来越多的学者开始从事电网发展评估方面的研究工作[4]。不同学者对构建电网发展评估指标有着不同的研究角度，如王智冬[5]等人从供电能力、电网资源配置能力、安全稳定水平等7个方面构建了电网发展指标体系；梁双[6]等人从基础性、技术性和经济性等3个方面出发建立指标体系能够较好地反映城市电网的整体性能；惠君伟[7]等人从电网安全性、容载比等5个方面构建了电网发展指标体系，并将指标体系应用于陕西输电网的发展水平评估，取得了较好的评估效果；王琬[8]等人从可靠性、安全性、经济性和协调性等4个方面构建了电网发展指标体系。可见，我国在电网发展水平评估方面的研究已经取得了一定成就。我国电网发展评估指标的构建主要考虑电网发展的安全性、经济性、供电质量、协调适应性、智能性等，已较为成熟和全面。相对于国内学者就电网发展水平的研究，国外学者研究更早，其所取得的成果也更为显著[3]。其中，美国和欧洲对电网发展水平评估的研究成果最为显著[9-10]。文献[11]提出的IBM智能电网成熟度模型将智能电网的成熟度划分为5个阶段，有利于明确各电网所处阶段和其发展方向。另外，还有美国能源部提出的从分布式能源技术、输配电基础设施等4个方面构建的智能电网发展评价指标体系[12]。欧洲国家提出以市场、环境、安全和电能质量为电网驱动因素的思路，构建以评价电网建设效益为目标的评价指标体系[12]。

综上可知，国内外对于电网发展评价的研究已较为深入，但是由于研究内容广泛，导致评价指标繁杂且不易获取[5-13]。归纳整理现有评价指标，将从电网发展的8个方面包括电网协调适应性、电网结构和供电能力等构建电网发展评价指标体系，力求指标内涵覆盖面广、指标意义明确且易得。

此外，在目前的电网发展评价研究工作中，采用的评价方法主要有层次分析法[14]、模糊综合评价[15]、灰色评价法[16]、组合评价法[17]等。这些方法多受主观因素影响，不能完全保证电网评估过程和结果的客观性；而客观评价方法也仅考虑指标在指标总体中的变异程度和对其他指标影响程度，未能对不同的评估对象赋予不同的权重。因此该文引入自学习综合评价法，自学习评价法是自学习技术在评价中的应用，其优点是不需要人工干预，可以完全排除人为因素，且学习能力强，满足对被评价对象的自适应性[18]，从而提高评价的针对性。基于贝叶斯推理的ANFIS不仅具有神经网络的自适应性和学习能力，还使神经网络的节点和权值具有明确的物理意义。贝叶斯推理将统计推断建立在后验分布的基础上，将贝叶斯推理用于ANFIS可着眼于整个参数空间的概率分布，在网络训练过程中自适应地调节正则化参数的大小，并使正则化参数达到最优。同时，在理论上也增加了ANFIS网络的鲁棒性和泛化能力，使得模型预测评价精度更高。

根据上述情况，该文采用贝叶斯推理改进的自适应神经模糊推理系统（adaptive network based fuzzy inference system，ANFIS）对电网发展水平进行评估。首先建立完善的电网发展水平评估指标体系，再利用基于贝叶斯网推理的ANFIS建立电网发展水平评估模型，最后选取浙江省某电网历史数据进行模型训练和测试，实例显示基于贝叶斯推理的ANFIS能够适应性地合理评估电网发展水平，且评估效果好。

1 基于贝叶斯推理的ANFIS的电网评估方法

1.1 自适应神经模糊推理系统（Basic ANFIS）

自适应神经模糊推理系统（ANFIS）有着模糊推理和神经网络的优点[19-20]。其典型的结构如图1所示。

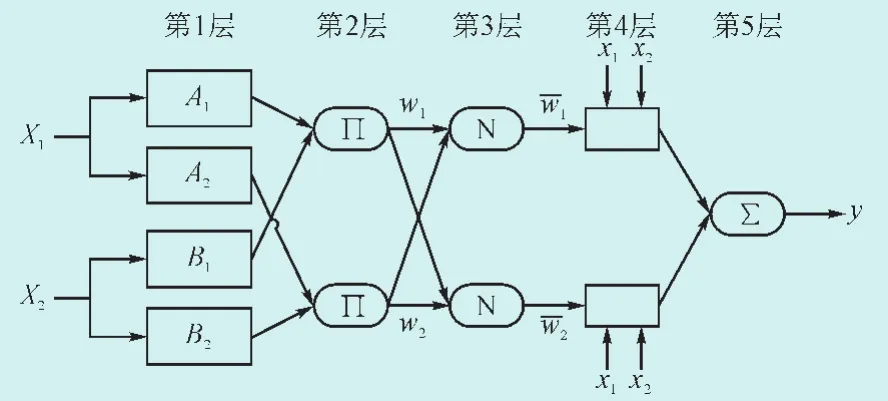
图1 ANFIS基本结构图Fig.1 Basic structure of ANFIS

其中，和是系统的输入，y是推理系统的输出，均为可提供的数据对。

第1层：模糊化层。

式中，Ai或Bj-2是模糊集，如“多”，“少”等；μAi（x1）和μBj-2（x2）是模糊集的隶属函数。

第2层：模糊推理层。

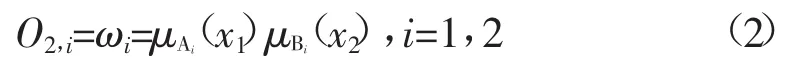
式中，ωi为每条规则的适用度。

第3层：标准化层。

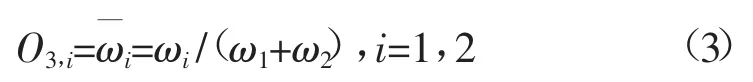
第4层：去模糊化层。

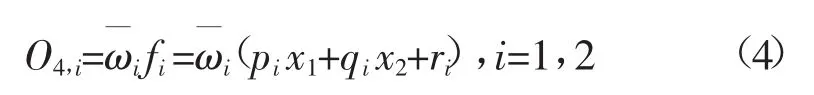
式中，{pi，qi，ri}是该结点的参数集。

第5层：输出层，此层的节点为单节点，为系统总输出。

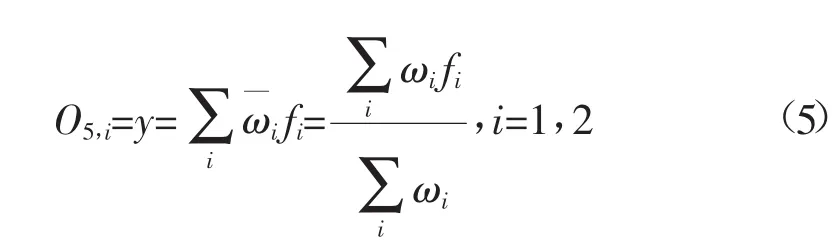
1.2 基于贝叶斯推理的ANFIS

贝叶斯推理将经验和知识作为先验信息，结合当前样本信息进行推断，同时不断完善以前的经验和知识，对以前的分布结果进行修正。因此，对参数估计越来越精准[10]。可用如下公式表示。

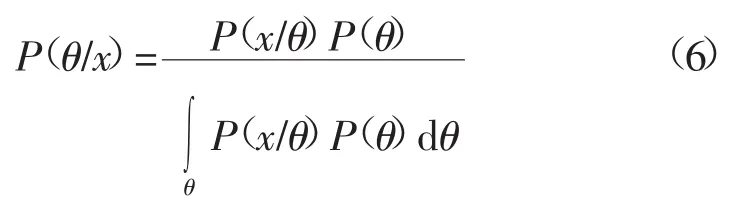
式中，P（θ/x）理解为抽样后的修正概率值，P（θ）理解为抽样前的认知概率值，P（θ/x）为P（θ）的调整的结果。

贝叶斯推理应用于ANFIS中的具体流程详见文献[21]。且误差函数ED为

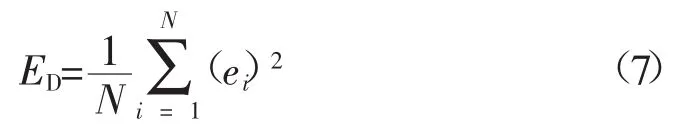
式中：N为样本总数；ei为误差。

为修正误差性能函数，增加一项[20]。即：

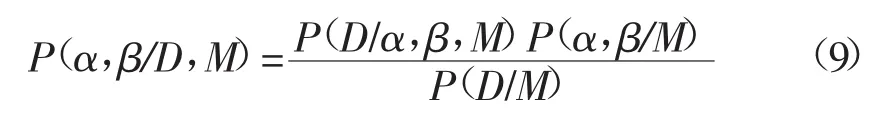
假设先验分布P（α，β/M）为较宽的分布函数。因此，若要使得α、β的后验分布结果达到最大值，则需使，P（D/α，β，M）达到最大值[20]。

若用M表示网络结构，在网络结构已确定的情况下，在样本数据缺少时，根据文献[20]有：

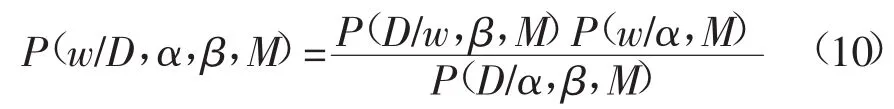
其中，P（w/α，M）为权值（阈值）的先验分布，W为权值向量，D为样本数据集，P（w/D，α，β，M）为权值的后验分布。

根据文献[11]和[21]，网络权值的先验分布P（w/α，M）服从高斯分布。

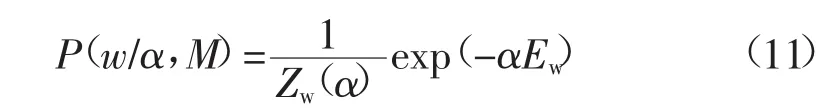
似然函数：

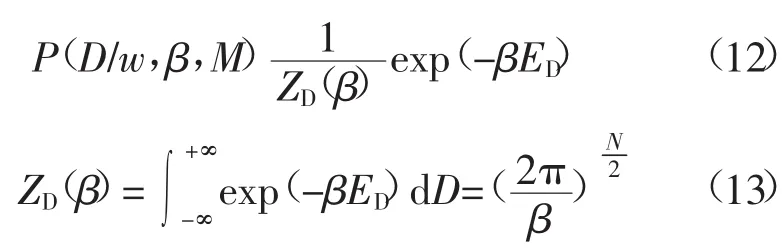
则，权值后验分布P（w/D，α，β，M）。

2 基于贝叶斯推理的ANFIS电网发展水平评估步骤

根据上述贝叶斯推理的ANFIS模型，电网发展水平评估流程如图2所示，归纳如下：

1）建立电网发展水平评估的指标体系，收集指标原始数据，并对数据进行归一化处理。

2）构建贝叶斯ANFIS电网发展水平评估模型。

3）产生评估模型训练样本，设置终止训练条件。

4）输入训练样本，训练模型，直到满足终止条件。

5）输入测试样本，计算贝叶斯ANFIS电网发展水平的综合得分，得出电网发展水平等级。

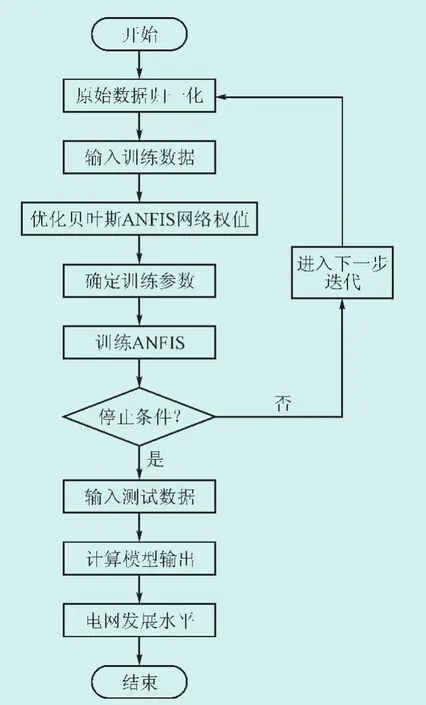
图2 基于贝叶斯推理的ANFIS电网发展水平评估流程图Fig.2 Flow chart of power grid developmental level evaluation based on ANFIS improved by Bayesian Inference

3 电网评估指标体系构建

3.1 电网评估指标体系

参考电网公司系统历年各类诊断分析工作、国网公司系统评价评估标准及南方电网公司、天津大学等配电网评估研究成果，整理形成电网评估指标体系[22-28]。其中配电网的评估指标体系中，单项指标层有8个，子指标层有22个，基本指标层有24个指标，如表1所示。

1）电网协调适应性

①对地区GDP贡献率（%）：被评估电网产值占当地GDP的比例。

②平均日负荷率（%）：被评估电网每日的平均负荷与最大负荷之比的百分比。

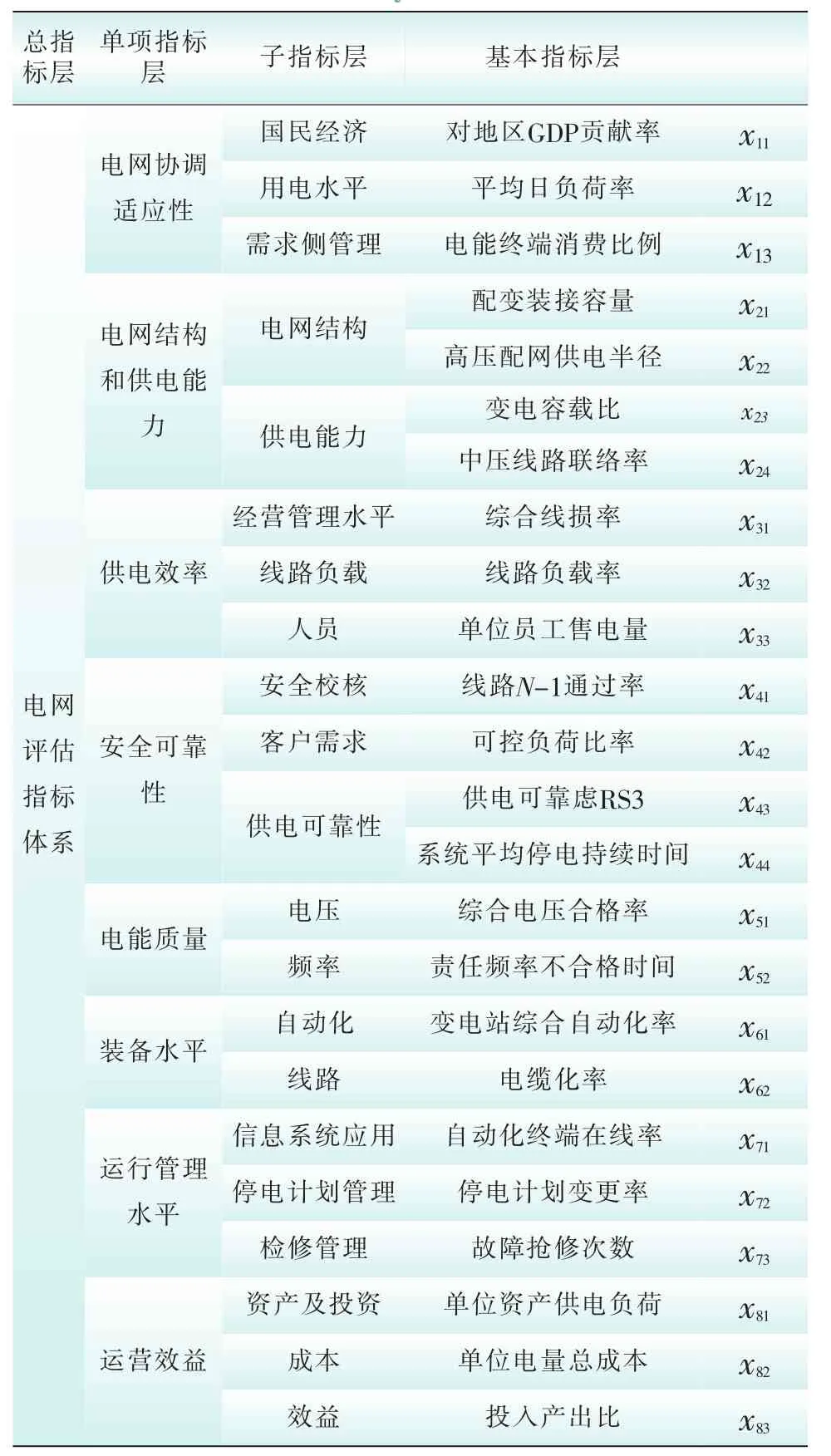
表1 配电网评估指标体系Tab.1 Evaluation index system of distribution network

③电能终端消费比例（%）：被评估电网所在地区电能消费占所有能源消费的比例。

2）电网结构和供电能力

①配变装接容量（kV·A/条）：用于中压配电网，反映每条中压线路的利用率，是平均每条中压线路的中压配变容量（kV·A）。

②高压配网供电半径（km）：用于110 kV、66 kV、35 kV电压等级的高压配网。

③变电容载比（kV·A/kW）：高压配电网中的某一层级供电区域内变电设备总容量（kV·A）与总负荷（kW）的比值。

④中压线路联络率（%）：是10 kV、20 kV线路满足互联结构的线路比例，为满足互联结构的线路条数与线路总条数之比。

3）供电效率

①综合线损率（%）：线损电量与供电量之比。

②线路负载率（%）：线路平均负荷与线路最大负荷之比。

④单位员工售电量（kW·h/人）：售电量与单位员工人数之比。

4）安全可靠性

①线路N-1通过率（%）：满足N-1原则的线路条数与线路总条数之比。

②可控负荷比率（%）：可控负荷与最大负荷之比。

③供电可靠率RS3（%）：不考虑因系统电源不足而需限电的停电事故的供电可靠程度。

④系统平均停电持续时间（h/（用户·a）））：表示系统在一年中每个用户的平均停电持续时间。

5）电能质量

①综合电压合格率：电压合格率通常包括A、B、C、D四类，针对给定母线监测点的电压合格率指标，公式为：

综合电压合格率为：

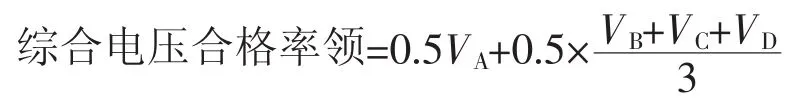
式中，VA、VB、VC、VD分别为A、B、C、D类电压合格率。

②责任频率不合格时间（s）：电网频率偏差超过规定范围的时间。

6）装备水平

①变电站综合自动化率（%）：适用于110 kV、60 kV、35 kV高压配电网，是实现综合自动化的变电站数目与变电站总数目之比。

②电缆化率（%）：电缆线路长度与线路总长度之比。

7）运行管理水平

①自动化终端在线率（%）：配网实时在线的终端总数与自动化终端投运总数之比。

②停电计划变更率（%）：停电计划变更次数与停电计划总次数之比。

③故障抢修次数：统计期间内，配电网发生故障抢修的次数。

8）运营效益

①单位资产供电负荷（kW/元）：统计期末配网供电负荷与统计期末配网资产总额之比。

（元/kW·h）：平均每kW·h电产生的总成本。

③投入产出比（%）：配电网规划建设所投入资金的回报程度，是运行收益与初始投资之比。

3.2 电网发展水平等级划分

本文以电网评估综合得分为评定电网发展水平的标准，如表2所示。

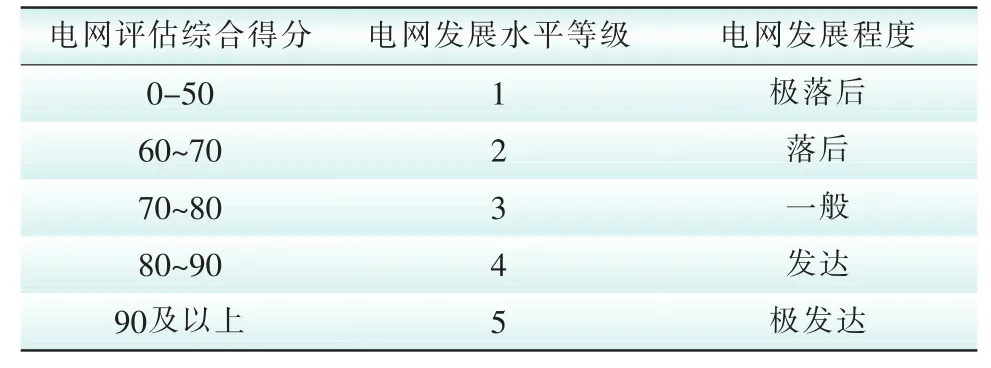
表2 电网发展水平等级划分Tab.2 Grid development level classification

4 算例验证

选取浙江省11个地级市电网2010-2015年电网评估指标数据进行算例验证。为保证电网评估指标和发展水平的全面性，共筛选出样本60个，其中用50个样本作为训练样本，占总样本的83.33%；10个样本作为测试样本，占总样本的16.67%。其中部分原始数据的部分指标如表3所示。所有样本的线路N-1通过率、系统平均停电持续时间、综合电压合格率和电缆化率如图3所示。

首先，对原始数据进行归一化处理。

式中，xn为样本数据归一化结果，x为样本原始数据，xmax和xmin分别为样本数据中的最大值和最小值。

在进行算法结果分析过程中，利用3个指标，包括相对误差（RE）、均方根误差（RMSE）、平均绝对误差（MAPE），其公式如下。

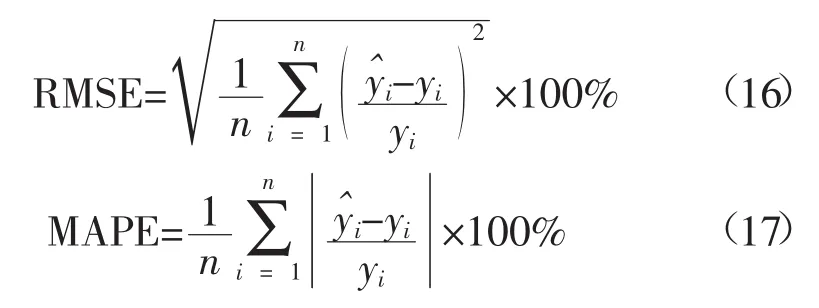
式中，yi为第i个样本的实际值，为第i个样本的模型计算值。

为能够做出对比，该文亦选取普通ANFIS模型、BP神经网络模型对上述数据进行测试计算。参数初始值设定。

①贝叶斯ANFIS

设定输入变量x和输出变量y的范围均为[-1，1]。在满足一定精度的前提下，每个变量在模糊化层仅取2个值，设定规则256条。采用广义的钟形函数，并选择hybrid算法，误差精度设置为0.001，训练次数为500。

②普通ANFIS

普通ANFIS设置参数同贝叶斯ANFIS。设定输入x和输出y的范围均为[-1，1]，每个变量在模糊化层仅取2个值，设定规则256条。采用广义的钟形函数，并选择hybrid算法，误差精度设置为0.001，训练次数为500。

③BP神经网络

BP神经网络的输入层、隐含层、输出层各层节点数分别为：12、8、1。最大训练次数为500；学习率0.01；训练要求精度为0.001；显示频率为20次；附加动量因子为0.95；最小性能梯度为1e-6；最大确认失败次数为5。训练函数为traingd。

将数据归一化结果输入上述设定好初始参数的各个模型中，采用MATLAB编程进行计算，得出预测结果如表4所示。

图4为贝叶斯ANFIS、普通ANFIS和BP神经网络3种模型训练误差迭代图。由图可知，贝叶斯ANFIS、普通ANFIS和BP神经网络分别在迭代119次、228次和249次时迭代停止，误差精度分别达到0.000 92、0.000 97和0.000 99（＜0.001）。可见，贝叶斯ANFIS算法能够快速收敛，可以在短时间内满足预期效果；也说明通过贝叶斯推理确定权重，能够提高ANFIS算法的非线性拟合能力，从而提升了算法的泛化能力。

表4为3种算法的模型测试结果，图5为3种算法的模型测试结果的误差对比图。将贝叶斯ANFIS、ANFIS和BP神经网络对样本的测试值进行对比发现，贝叶斯ANFIS测试值与实际值之间的最大间隙为1.41，小于ANFIS模型的3.88和BP模型的5.46；贝叶斯ANFIS预测值与实际值之间的最小间隙为0.38，小于ANFIS模型的0.76和BP模型的1.68，说明贝叶斯ANFIS模型的测试结果更加稳定。

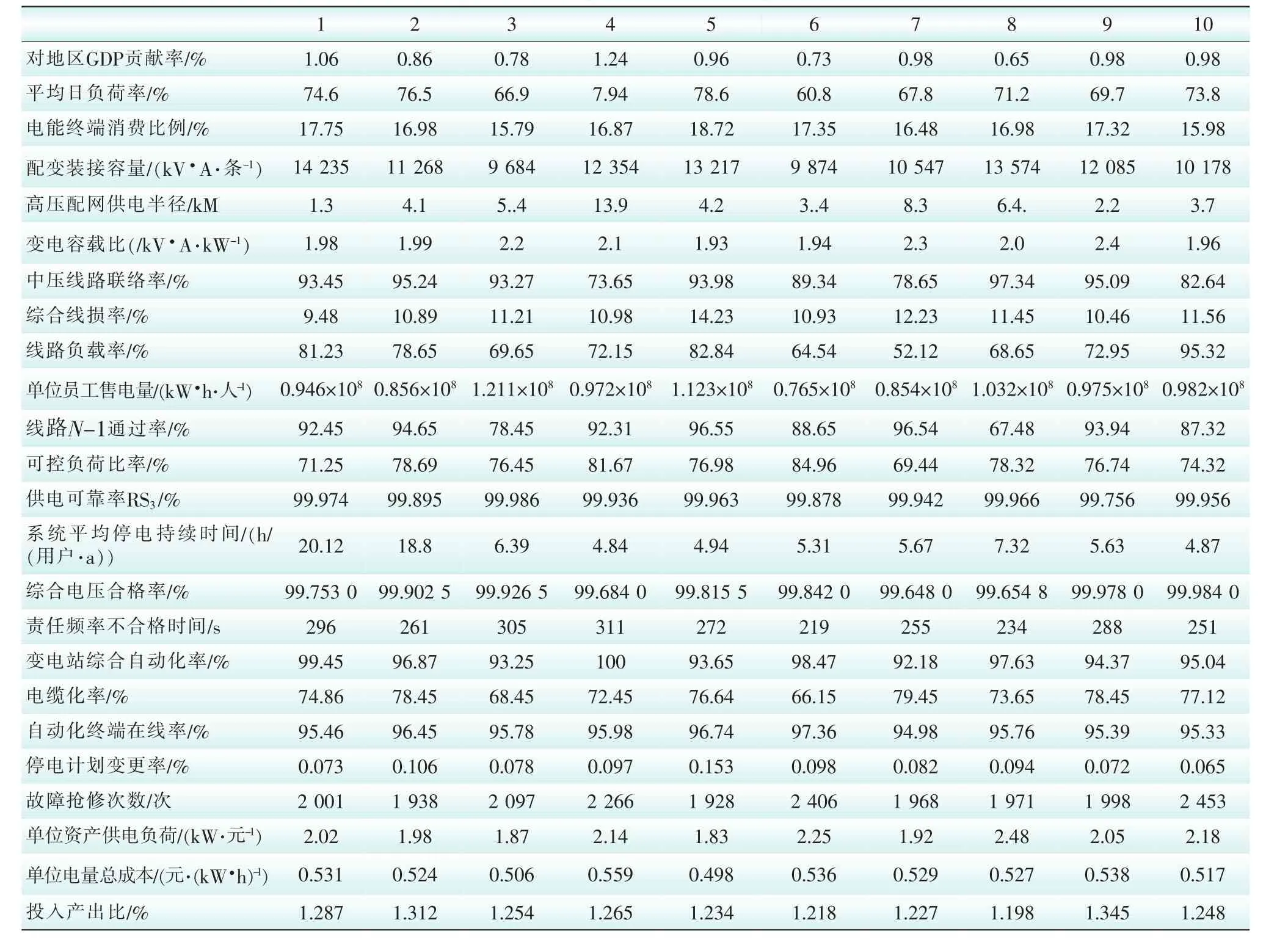
表3 电网发展水平评估指标部分原始数据Tab.3 Part of the original data of power grid development level evaluation index

图3 线路N-1通过率、系统平均停电持续时间、电压合格率和电缆化率数据Fig.3 Line N-1 pass rate，system average interruption duration，voltage qualified rate and cable rate data

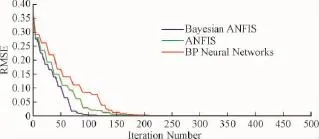
图4 误差精度迭代图Fig.4 Error precision iteration

贝叶斯ANFIS、ANFIS算法和BP神经网络算法的相对误差绝对值最大分别为1.83%、4.46%和5.91%，最小分别为0.60%、1.31%，2.26%，说明贝叶斯ANFIS模型精度更高。均方根误差为了衡量测试值与真实值之间的变化程度，如表4所示，贝叶斯ANFIS、ANFIS算法和BP神经网络算法的均方误差分别为1.25%、2.84%和3.90%，说明贝叶斯ANFIS测量值与真值的偏差最小，预测效果更好。另外，也可以看出，贝叶斯ANFIS网络的平均绝对误差最小。说明贝叶斯ANFIS模型的总体预测精度最高，算法的非线性映射能力更佳，更加适用于电网发展水平的评估。

贝叶斯ANFIS进行电网发展水平评估结果中，发展程度为极发达的样本有2个，发展程度为发达的样本有3个，发展程度为一般的样本有2个，发展程度为落后的样本有2个，发展程度极落后的样本有1个，电网发展程度评估正确率为100%。

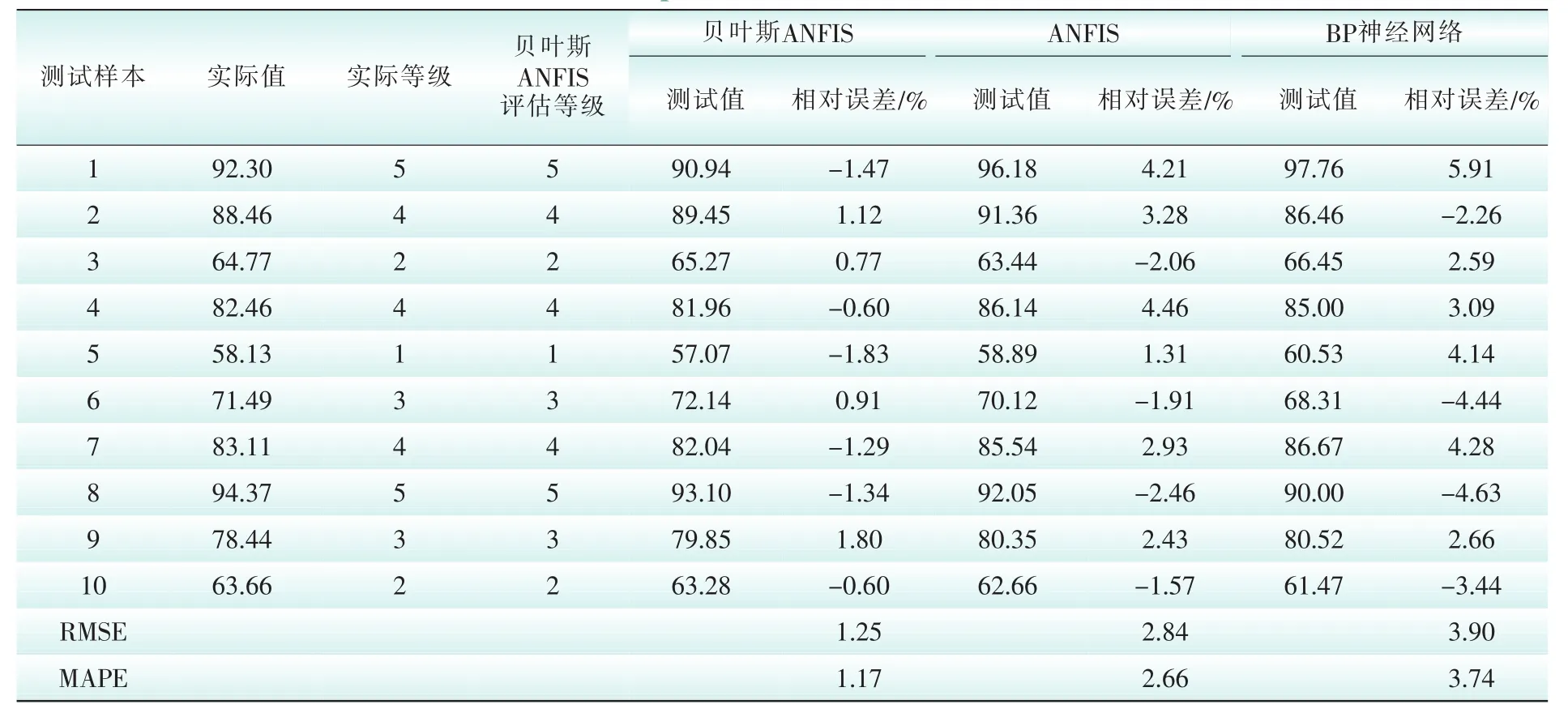
表4 实际值与测试值对比表Tab.4 Comparison of actual and test values

图5 各算法相对误差对比图Fig.5 Relative error of each algorithm

5 结语

该文根据评估需求，建立了全面合理的电网评估指标体系；进而将贝叶斯推理应用于ANFIS算法，建立了贝叶斯ANFIS电网发展水平评估模型，对电网发展水平进行评估。本文选取浙江省部分地级市2010-2015年作为案例进行了模型测试和验证，结果表明：贝叶斯ANFIS系统能够不断优化其网络参数，有着较好的学习能力和适应能力；并与ANFIS算法和BP神经网络模型进行对比，可以发现贝叶斯ANFIS模型有着更高的预测精度和更强的鲁棒性，对电网发展水平有着更好的评估效果。

[1]韩柳，彭冬，王智冬，等.电网评估指标体系的构建及应用[J].电力建设，2010，31（11）：28-33.HAN Liu， PENG Dong，WANG Zhidong，etal.Constitution and application of the index system for powergrid assessment[J].Electric Power Construction，2010，31（11）：28-33.

[2]杨江.电网发展协调性评价指标体系研究[J].陕西电力，2016，44（8）：55-59.YANG Jiang.Study on development coordination evaluation indicatorssystem of power grid[J].Shaanxi Electric Power，2016，44（8）：55-59.

[3]边二朝.地区电网发展水平诊断体系及应用研究[D].北京：华北电力大学，2014.

[4]李丽颖，孙跃国.电网可靠性评估的建模和仿真研究[J].计算机仿真，2012（4）：084.LI Liying，SUN Yueguo.Modeling and simulation of power reliability evaluation[J].Computer Simulation，2012（4）：084.

[5]王智冬，黄怡，靳晓凌，等.我国电网发展评价指标体系研究[J].东北电力大学学报，2009，29（4）：83-86.WANG Zhidong，HUANG Yi，JIN Xiaoling，et al.Study on evaluation indexes of power grid development[J].Journal of Northeast Dianli University，2009，29（4）：83-86.

[6]梁双，范明天，苏剑.城市电网性能评价指标框架的研究[J].供用电，2009，26（5）：8-11.LIANG Shuang，FAN Mingtian，SU Jian.Research on the evaluation index framework of urban power network[J].Distribution&Utilization，2009，26（5）：8-11.

[7]惠君伟，李复明，王新，等.陕西“十一五”输电网发展水平分析[J].陕西电力，2010，38（11）：94-97.HUI Junwei，LI Fuming，WANG Xin，et al.Analysis on development status of shaanxi transmission grid during the eleventh five-year plan[J].Shaanxi Electric Power，2010，38（11）：94-97.

[8]王琬，刘宗岐，曾博，等.大都市电网综合指标体系与评价模型[J].现代电力，2011，28（4）：24-28.WANG Wan，LIU Zongqi，ZENG Bo，et al.Comprehensive index system and evaluation model of power grid for metropolitan cities[J].Modern Electric Power，2011，28（4）：24-28.

[9]KUKDE P K，SATHE D A，KULKARNI S V.Accelerated power development and reform programme in india[C]//Power Engineering Society General Meeting，2004.IEEE.IEEE，2004：2346-2352.

[10]MUKHOPADHYAY S，DUBE S K，SOONEE S K.Development of power market in India[C]//Power Engineering Society General Meeting，2006.IEEE.IEEE，2006：4 pp.

[11]徐秋卉.基于灰色关联和组合赋权的智能输配电网综合评价研究[D].北京华北电力大学，2015.

[12]U.S.Department of energy.smart grid system report[R].New York：U.S.Department of Energy，2009.

[13]EUROPEAN SMART GRIDS Technology platform.strategic deployment document for europe’s electricity networks of the future[R].Brussels：European Commission，2008.

[14]陆嘉铭，高洁.基于主成分分析法的线损指标评价[J].华东电力，2014，42（9）：1817-1820.LU Jiaming，GAO Jie.Index evaluation of line loss based on principal component analysis[J].East China Electric Power，2014，42（9）：1817-1820.

[15]徐志勇，张徐东，曾鸣，等.基于ANP的多层次模糊综合评价法的电网建设项目后评价研究 [J].华东电力，2009，37（3）：488-491.XU Zhiyong，ZHANG Xudong，ZENG Ming，et al.Application of aNP-based multilevel fuzzy comprehensive evaluation methods to post-evaluation for grid construction projects[J].East China Electric Power，2009，37（3）：488-491.

[16]崔明建，孙元章，杨军，等.一种基于多层次灰色面积关联分析的电网安全综合评价模型 [J].电网技术，2013，37（12）：3453-3460.CU Mingjian，SUN Yuanzhang，YANG Jun，et al.Power grid security comprehensive assessment based on multilevel grey area relational analysis [J].Power System Technology，2013，37（12）：3453-3460.

[17]SUN Q，GE X，LIU L，et al.Smart grid multi-attribute network process comprehensive evaluation method and Its application[J].Power System Technology，2012，36（10）：1-5.

[18]姬波.信息瓶颈方法的特征权重研究 [D].郑州：郑州大学，2013.

[19]吴江潦，易灵芝，彭寒梅，等.开关磁阻电机自适应模糊神经网络系统（ANFIS）无位置传感器控制[J].煤炭学报，2010，35（8）：1401-1405.WU Jiangliao，YI Lingzhi，PENG Hanmei，et al.Position sensorless control of the switched reluctance motor using adaptive network fuzzy inference system （ANFIS）[J].Journal of China Coal Society，2010，35（8）：1401-1405.

[20]李鹏程，陈国华，张力，等.基于ANFIS的人因失误风险严重度识别[J].中国安全科学学报，2014（1）：72-77.LI Pengcheng，CHEN Guohua，ZHANG Li，et al.An ANFIS-based approach to identifying criticality of human error risk[J].China Safety Science Journal，2014（1）：72-77.

[21]李鹏.基于贝叶斯理论的神经网络算法研究 [J].光机电信息，2011，28（1）：28-32.LI Peng.Research of neural network algorithm based onbayes theory[J].Ome Information，2011，28（1）：28-32.

[22]孙鹏.地区配电网综合评估体系研究 [D].济南：山东大学，2014.

[23]黎小华，夏小平，程文辉，等.冰蓄冷空调系统供冷项目决策评价方法及应用[J].节能技术，2016（1）：77-80.LI Xiaohua，XIA Xiaoping，CHENG Wenhui，et al.Project decision evaluation method and its application of ice storage air conditioning systems[J].Energy Conservation Technology，2016（1）：77-80.

[24]薛晓强，叶辛，汪鸿.电网企业能源管理体系的模糊综合评价[J].节能技术，2015（6）：546-549，553.XUE Xiaoqiang，YE Xin，WANG Hong.The fuzzy comprehensive evaluation of power grid enterprises energy management system[J].Energy Conservation Technology，2015（6）：546-549，553.

[25]段秦刚，邓应松，王子力.用户侧微电网技术经济评价研究综述[J].陕西电力，2015，43（7）：58-62，97.DUAN Qingang，DENG Yingsong，WANG Zili.Probe into user side micro-grid technological economic evaluation study[J].Shaanxi Electric Power，2015，43（7）：58-62，97.

[26]刘洋洋，何永秀.国内外电网规划经济评价对比分析[J].陕西电力，2014，42（7）：52-56，93.LIU Yangyang，HE Yongxiu.Comparative analysis of economic evaluation in domestic and international power network planning[J].Shaanxi Electric Power，2014，42（7）：52-56，93.

[27]饶尧，邱泽晶，彭旭东.基于层次分析法的电网能效影响因子分析研究[J].节能技术，2014（1）：51-54.RAO Yao，QIU Zejing，PENG Xudong.Analysis of grid energy efficiency factors based on analytic hierarchy process[J].Energy Conservation Technology，2014（1）：51-54.

[28]杨帆，赵书强.智能电网的发展对大电网可靠性评估的影响[J].电网与清洁能源，2013，29（10）：24-30+36.YANG Fan，ZHAO Shuqiang.Impact of smart grid development on composite power system reliability evaluation[J].Power System and Clean Energy，2013，29（10）：24-30+36.

（编辑 徐花荣）

Evaluation of Power Network Developmental Level Based on ANFIS Improved by Bayesian Inference

NIU Dongxiao1，LIU Weidong2，HUANG Yali1，SUN Ke2，LIU Hongfei1，WU Han1
（1.School of Economics and Management，North China Electric Power University，Beijing 102206，China；2.Economy Research Institute of State Grid Zhejiang Electric Power Company，Hangzhou 310000，Zhejiang，China）

The evaluation of the development level of power grids is the reliable premise and basis for the power grid planning and construction.In this paper，first of all，we establish a comprehensive and reasonable index system to evaluate the development level of power grids；and then build theevaluation modelthrough ANFIS based on Bayesian inference.Finally，historical data of a certain power grid in Zhejiang Province is selected to train and test the model.The numerical example show the effectiveness of the model proposed.

power grid assessment；Bayesian inference；adaptive network based fuzzy inference system（ANFIS）

2017-01-07。

牛东晓（1962—），男，博士，教授，博士生导师，研究方向为项目预测与决策理论及其应用、项目综合评价方法及其应用的研究等；

刘卫东（1975—），男，高级工程师，主要从事电网规划研究、工程建设管理；

黄雅莉（1991—），女，硕士研究生，研究方向为输电线路覆冰预测、输配电网评估方法及应用的研究；

孙 可（1980—），男，高级工程师，主要从事电网发展研究，电网工程前期设计管理；

刘鸿飞（1990—），男，硕士研究生，研究方向为输配电网评估方法与应用；

吴 晗（1993—），女，硕士研究生，研究方向为输配电网评估方法与应用。

国家自然科学基金（71471059）。

Project Supported by the National Natural Science Foundation of China（71471059）.

1674-3814（2017）03-0008-09

TM715

A