改进最小二乘支持向量机电量预测算法

杨柳，吴延琳，张超，刘超，蒋勃，张鹏

（1.国网陕西省电力公司，陕西西安 710048；2.国网陕西省电力公司经济技术研究院，陕西西安 710065）

改进最小二乘支持向量机电量预测算法

杨柳1，吴延琳2，张超1，刘超2，蒋勃1，张鹏2

（1.国网陕西省电力公司，陕西西安 710048；2.国网陕西省电力公司经济技术研究院，陕西西安 710065）

基于电量数据内在规律及与外界环境变量关系的深度挖掘，定义了占季比指标，提出了最小二乘支持向量机算法与基于占季比预测相结合的电量预测混合算法；根据国内A省历史分月电量进行实际算例分析，通过Elman神经网络、BP神经网络预测方法与文中所提方法的预测误差对比，验证了所提算法的预测精度，证明所提算法对预测精度有较大提高。

电量预测；Elman神经网络；最小二乘支持向量机；占季比

负荷电量预测是电网规划、营销与调度运行的基础，伴随着“互联网+”与智能电网建设，电网规划、智能营销、智能调度等都对电量预测精度提出了更高的要求。目前，电力系统的电量和负荷预测方法主要有3种[1]：综合用电水平法、单耗法、弹性系数法等[2-3]经典预测方法；时间序列法、回归分析法、趋势外推法等[4-6]传统的预测方法；神经网络法、小波分析法、支持向量机等新型预测算法[7-10]。

随着电网运行管理对电量预测精度的要求越来越高，电量预测方法逐步在改进优化，有历史研究[11-14]采用多种方法对传统模型的参数优化改进，使得传统模型同历史数据更吻合：文献[15-17]利用新方法对历史数据进行训练拟合及分解重构，取得了良好的效果；文献[18-22]基于传统算法或新兴算法采用组合预测，从而减小模型预测残差。但是，上述研究只通过新型算法对历史数据进行高级处理，或者割裂数据本身的变化规律和外部因素的关系等，都存在一定的不足。本文预测模型不仅充分考虑电量数据的自身变化规律，还考虑其他因素与电量之间的关系，提出了电量占季比预测与最小二乘支持向量机算法相结合的电量预测混合算法。

1 电量数据分析及模型选择

文中对A省2009—2015年电网的实际年度、季度和月度电量数据特点，与行业用电、经济数据关系进行了分析。年度电量数据序列基本上呈单调递增的，因此，对于年度电量可以用趋势外推、灰色预测、线性回归等较简单方法进行预测。季度电量序列和月度电量序列表现出增长性和波动性的二重趋势，见图1。采用上述方法预测精度较低。所以，必须根据季度、月度电量数据的特点选取基础预测模型来构建适合于季度、月度电量预测的算法。

图1 国内A省电网电量历史数据序列Fig.1 Electricity consumption historical data of A province

GDP与城市电网电量数据的变化规律在一定程度上表现出一致性，为体现地区电量数据的变化特点，在电量模型中引入经济指标作为外部参考因素，能更加准确的拟合电量数据的真实变化过程。

2 支持向量机与人工神经网络算法

2.1 最小二乘支持向量机算法

支持向量机（support vector machine）是应用结构风险最小化原则设计的学习机器，它是统计学习理论中重要且实用的部分[12]。SVM最初研究的是模式识别中的线性可分的分类问题。支持向量回归机就是在分类问题的基础上演变过来的，二者不同之处在于分类问题输出变量只能为2个不同的值；而回归问题输出变量能取任意实数值。

最小二乘支持向量机（LSSVM）是对SVM的一种改进，它是将传统SVM中的不等式约束改为等式约束，把求解二次规划问题转化为求解线性方程组问题，从而提高了问题求解的速度和收敛精度。其算法原理如下：

支持向量回归机根据训练样本S={（x1，y1），…，（xl，yl）}⊂Rn×R构造回归函数：

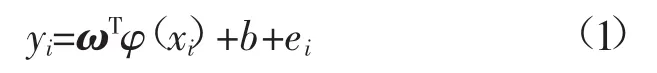
定义损失函数为

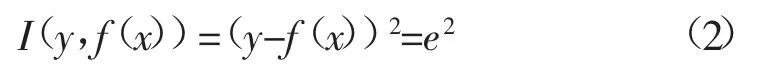
根据结构风险最小化原理，最小二乘支持向量机的风险函数为

据此可以得到原始最优化问题：

正实数γ是惩罚系数。LSSVM通过定义与标准SVM不同的损失函数，将不等式约束改为等式约束。

构造拉格朗日函数：

式中：αi为拉格朗日乘子。

将各变量导数置为零，消去ω和e，得线性方程：

式中：Iv=［1，1，…，1］T；对角矩阵Dγ=diag［γ，γ，…，γ］；y=［y1，y2，…，yl］T；α=［α1，α2，…，αl］T；矩阵Ω的各元素为

核函数K（x，xi）目的是解决原始空间中不能线性回归问题。支持向量机线性到非线性回归是通过核函数来实现的，本文选用的是高斯径向基核函数K（xi，x）=exp［－|x－xi|2/σ2］。

求解方程可得到α和b，则回归函数为

在对LSSVM进行回归预测时，惩罚系数γ与径向基核函数核参数σ对回归函数预测的精度至关重要，因此需要对以上两个参数进行优化。本文通过采用网格搜索算法进行参数寻优，并选用三折交叉验证法对网格寻优的效果进行仿真验证。

基于最小二乘支持向量机的电量预测流程是首先进行原始数据预处理，然后优化LSSVM的两个重要参数，在得到最优参数后，将训练集和最优参数输入到LSSVM中，训练得到相应的预测模型，然后再输入测试数据，得到预测结果，最后对预测结果进行评价与分析。

2.2 人工神经网络预测算法

本文主要将BP神经网络以及Elman神经网络应用于电量预测中,并作对比分析。BP（back propagation）神经网络为阶层型神经网络，由输入层、中间层、输出层组成，中间层可扩展为多层，见图2。将一对学习模式提供给BP网络，神经元获得输入响应产生连接权值（weight）。然后按照减小希望输出与实际输出的误差方向，从输出层经各中间层逐层修正各连接权，并回到输入层。此过程反复交替，直至全局误差趋向给定的极小值。

图2 典型BP神经网络结构Fig.2 Typical BP neural network structure

Elman回归网络是一种典型的动态神经元网络，能够更生动、更直接反映系统动态特性，它是在BP人工神经网络基本结构的基础上，通过存储内部状态使其具备映射动态特征的功能，从而使系统具有适应时变特性的能力。

Elman回归神经元网络一般分为4层：输入层、中间层（隐含层）、承接层和输出层，如图3所示。其输入层、隐含层和输出层的连接类似于前馈网络，输入层单元仅起信号传输作用，输出层单元起线性加权作用。隐含层单元的传递函数可采用线性和非线性函数；承接层又称为上下文层和状态层，用来记忆隐含层单元的前一时刻输出值。

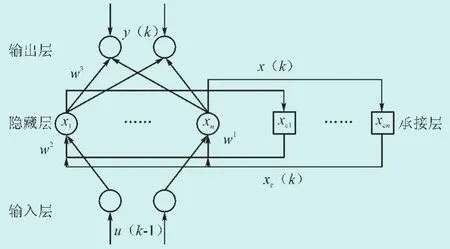
图3 Elman神经网络结构Fig.3 Elman neural network structure

Elman回归神经元网络的特点是通过承接层的延迟与存储，隐含层的输出自联到隐含层的输入，增加了网络本身处理动态信息的能力，从而达到了动态建模的目的。此外，Elman回归神经网络能够以任意精度逼近任意非线性映射。根据电量的数据，选定反馈神经网络的输入、输出节点来反映电力系统电量的内在规律，从而达到预测未来时段电量的目的。

3 算法测试

所有测试算法的实验环境均为MATLAB R2010a，实验数据来自A省实际电量数据，时间分辨率为月。

3.1 BP神经网络算法算例分析

考虑售电量季节周期性变动和逐步增长的特点，以及GDP季度性变动对售电量的影响，在预测某月的售电量时，采用BP神经网络法先对该月所在季度的售电量进行预测。训练样本输入采用2012、2013年分月电量与GDP数据，输出为2014年相应月电量；预测样本采用2013、2014年分月电量与GDP数据，输出为预测年2015年相应月电量，2015年A省分月电量预测结果如图4所示。

图4 BP神经网络电量预测结果Fig.4 Monthly electricity consumption prediction result by BP neural network

BP神经网络算法预测结果绝对误差最大为-8.275 7亿kW·h；相对误差最高为12.31%；相对平均误差为3.44%。但预测结果相对误差波动性大。

3.2 Elman神经网络算法算例分析

Elman神经网络算法训练样本和预测样本与BP神经网络算法保持一致。2015年A省分月电量预测结果如图5所示。

ELman神经网络算法预测结果绝对误差最大为5.255 2亿kW·h；相对误差最高为7.38%；相对平均误差为3.7%；略高于BP神经网络。但由于其相对误差波动性较低，具有更高的实际应用。

以上2种预测方法未能充分考虑售电量季节周期性变动和逐步增长的特点，无法消除单月由于时间短、随机波动性大带来的误差。

图5 Elman神经网络预测结果Fig.5 Monthly electricity consumption prediction result by Elman neural network

4 基于外推法占季比和支持向量机预测算法的算例分析

4.1 提高预测精度的方法

历年各季度售电量按时间序列既有逐步增长趋势，又有季节周期性变动，为了查明历年各季度售电量与该季度各个月售电量之间的关系，定义“占季比”ζ为各月度售电量占所在季度的季度售电量的比重，即ζ=某月售电量/该月所在季度的季度售电量。

通过对A省地区历年数据挖掘分析，可以得出以下重要结论：1）历年各季度售电量按时间序列既有逐步增长趋势，又有季节周期性变动；2）各月历年的占季比ζ都在一个稳定值附近上下微小波动。根据历史数据分析得出的规律特点，建立月度售电量预测新方法，步骤如下：

1）在预测某月售电量时，采用最小二乘支持向量机法先对该月所在季度的季度售电量进行预测。

2）根据历史数据，进行占季比的预测。通过寻找占季比的变化趋势，并根据这一变化趋势对已有数据序列作计算外推和曲线拟合外推，从而求得占季比的预测值。

3）利用步骤1预测出的月所在季度的季度售电量Y和占季比的预测值，计算出预测月度售电量。

4.2 算法测试

设置最小二乘支持向量机（LSSVM）参数的寻优范围为γ=［20，30］，σ2=［40，60］步长分别设置为0.5和1。采用3折交叉验证参数合理性。

选取A省2011—2015年实际总电量进行验证。其中2011-2014年数据作为训练样本，2012-2015年的数据作为预测样本。以2011-2013年同期的季度电量、季度GDP作为训练样本的输入；以2014年同期的季度电量、季度GDP作为训练样本的输出，训练出合适的模型。将2012—2014年同期的季度电量、季度GDP作为输入变量带入训练好的模型中，得到2015年预测的季度电量，再根据每个月电量占该季度的比例分配到每个月，从而预测出每个月的电量。预测结果用绝对误差、相对误差、平均相对误差来描述。在输入模型之前，原始数据已经过筛选，以保证其连续性和合理性。

在基于LSSVM的预测中，训练样本作用是训练出合适模型，将预测季度的输入变量代入训练好的模型，得到预测电量。

选取预测季度之前3年同期的季度电量、季度GDP作为输入变量，利用网格寻优法对LSSVM参数（γ，σ2）进行优化，然后输入模型对未来4个季度的电量进行预测，选择MCC的高斯径向基核函数参数为0.1，结果如图6所示。

图6 基于占季比预测的LSSVM电量预测结果Fig.6 Monthly electricity consumption prediction result by EMSR-LSSVM hybrid method

预测结果绝对误差最大为2.291 3亿kW·h；相对误差最高为3.08%；相对平均误差为1.91%。相对上述2种算法，相对误差最大值与平均误差明显降低，且相对误差值波动性较小，见表1。

5 结论

本论文对最小二乘支持向量机模型电量预测算法进行改进，提出了基于占季比预测与最小二乘支持向量机的混合算法，并与理论先进、预测精度高的BP神经网络算法和Elman神经网络算法电量预测结果进行对比，得出如下结论：

1）Elman神经网络算法预测结果平均相对误差值略高于BP神经网络算法，但相对误差值波动性小，最大相对误差值小于BP神经网络。

2）相比BP神经网络、Elman神经网络2种算法，改进算法预测结果最大相对误差值与平均相对误差均明显降低，预测精度明显提高，预测结果对电网规划、调度、营销等具有较高的指导意义。

表1 预测结果对比表Tab.1 Comparison of prediction results

[1]牛东晓，曹树华，卢建昌，等.电力负荷预测技术及其应用（第二版）[M].北京：中国电力出版出版社，2009.

[2]凌建凤.线损管理下的供、售电量分析及预测[D].上海：上海交通大学，2007.

[3]赵美丽.电力营销决策支持系统中的电量预测分析与研究[D].天津：河北工业大学，2007.

[4]杨云莹，任玉珑，段锴.基于虚拟变量与时间序列法的电量需求预测[J].电力需求测管理，2011，13（5）：17-20.YANG Yunying，REN Yulong，DUAN Kai.Based on dummy variables and time sequence method of electric power de-mand forecasting[J].The Demand of Electric Power Mea-surement Management，2011，13（5）：17-20（in Chinese）.

[5]KANDIL M S，EI-DEBEIKY S M，HASANIEN N E.Overvierw and comparison of long-term forecasting techniques for a fast developing utility[J].Electric Power Systems Research，2001，58（1）：11-17.

[6]周淼.湖南省人均需电量回归模型的建立及其预测应用[J].中南林业科技大学学报，2010，4（4）：75-77.ZHOU Miao.Hunan province per capita need power regression model establishment and application[J].Journal of Central South University of Forestry and Technology Forecasting，2010，4（4）：75-77（in Chinese）.

[7]PARK D C，EI-SHARKAWI M A，MARKS J，et al.Electric load forecasting using a neural network[J].IEEE Trans on Power Systems，1991，6（2）：442-449.

[8]CHUI C K.An introduction to wavelets[M].New York：Academic Press，1992.

[9]赵登福，庞文晨，张讲社，等.基于贝叶斯理论和在线学习支持向量机的短期电量预测[J].中国电机工程学报，2007，25（13）：8-13.ZHAO Dengfu，PANG Wenchen，ZHANG Jiangshe，et al.Short term forecasting of short term load based on bayesian theory and online learning support vector ma-chine[J].Proceedings of the Chinese Society of Electrical Engineering，2007，25（13）：8-13（in Chinese）.

[10]顾峰，艾芊，凌建凤.组合预测方法在电力负荷预测中的应用[J].中国电力，1998，31（6）：3-5.GU Feng，AI Qian，LING Jianfeng.Application of combination forecasting method in the power load forecast in power China[J].Electric Power，1998，31（6）：3-5（in Chinese）.

[11]周德强.改进的灰色Verhulst模型在中长期负荷预测中的应用[J].电网技术，2009，33（18）：3-5，124-127.ZHOU Deqiang.Application of improved grey verhulst model in medium and long term load forecasting[J].Power System Technology，2009，33（18）：3-5，124-127（in Chinese）.

[12]唐杰明，刘俊勇，杨可，等.基于灰色模型和最小二乘支持向量机的电力短期负荷组合预测[J].电网技术，2009，33（3）：63-68.TANG Jieming，LIU Junyong，YANG Ke，et al.Short term load forecasting based on grey model and least square support vector machine[J].Power System Technology，2009，33（3）：63-68（in Chinese）.

[13]周德强，武本令.灰色BP神经网络模型的优化及负荷预测[J].电力系统保护与控制，2011，39（21）：66-69.ZHOU Deqiang，WU Benling.Grey BP neural network model optimization and load forecasting[J].Electric Power System Protection and Control，2011，39（21）：66-69（in Chinese）.

[14]KHASHEI M，BIJARI M.A novel hybridization of artificial neural networks and ARIMA models for time series forecasting[J].Applied Soft Computing，2011（11）：2664-2675.

[15]吴景龙，杨淑霞，刘承水.基于遗传算法优化参数的支持向量机短期负荷预测方法[J].中南大学学报（自然科学版），2009，40（1）：180-184.WU Jinglong，YANG Shuxia，LIU Chengshui.Short term load forecasting method based on genetic algorithm optimization parameter support vector machine[J].Journal of Central South University（Natural Science Edition），2009，40（1）：180-184（in Chinese）.

[16]JAMES W T，BUIZZA R.Electric load forecasting using a neural net work with weather ensemble predictions[J].IEEE Trans on Power Systems，2002，17（3）：626-632.

[17]GONZÁLEZ-ROMERA E，JARAMILLO-MORÁN M A，CARMONA-FERNÁNDEZ D.Monthly electric energy demand forecasting based on trend extraction[J].IEEE Trans on Power Systems，2006，21（4）：1946-1953.

[18]康重庆，夏清，沈瑜，等.电力系统负荷预测的综合模型[J].清华大学学报（自然科学版），1999，39（1）：8-11.KANG Chongqing，XIA Qing，SHEN Yu，et al.A comprehensive model of power system load forecasting[J].Journal of Tsinghua University（Natural Science Edition），1999，39（1）：8-11（in Chinese）.

[19]李小龙，李郁侠，师彪，等.改进粒子群算法在中长期电力负荷组合预测模型中的应用[J].武汉大学学报（工学版），2011，44（3）：380-382，387.LI Xiaolong，LI Yuxia，SHI Biao，et al.Improved particle swarm optimization algorithm in the medium and long term power load combination forecasting model of application[J].Wuhan University Journal（Engineering and Technology Edition），2011，44（3）：380-382，387（in Chinese）.

[20]金鑫，罗滇生，孙广强，等.中长期电力负荷预测模型筛选与组合方法[J].电力系统及其自动化学报，2012，24（4）：150-155.JIN Xin，LUO Diansheng，SUN Guangqiang，et al.Selection and combination method of medium and long term power load forecasting model[J].Journal of Electric Power System and Its Automation，2012，24（4）：150-155（in Chinese）.

[21]吴耀武，娄素华，卢斯煜，等.基于改进的D-S证据理论的中长期负荷预测方法[J].电工技术学报，2012，27（8）：157-162.WU Yaowu，LOU Suhua，LU Siyu，et al.Based on improved D-S evidence theory in mid long term load forecast method[J].Transactions of China Electrotechnical Society，2012，27（8）：157-162（in Chinese）.

[22]WIDODO A，BUDII I.Combination of time series forecasts using neural network[C]//International Conference on Electrical Engineering and Informatics，Bandung，Indonesia，2011.

An Improved Electricity Consumption Prediction Method of Least Squares Support Vector Machine

YANG Liu1，WU Yanlin2，ZHANG Chao1，LIU Chao2，JIANG Bo1，ZHANG Peng2
（1.State Grid Shaanxi Electric Power Company，Xi’an 710048，Shaanxi，China；2.State Grid Shaanxi Electric Power Company Economic Research Institute，Xi’an 710065，Shaanxi，China）

Basing on the inherent law of electric data and the relationship of external environment，theelectricity monthseason ratio（EMSR）is defined.Proposing the improved power prediction algorithm that combines least squares support vector machine algorithm and the quarterly EMSR forecast algorithm.The monthly power data of province A is used to do the verification.By comparing the forecast error of Elman neural network，BP neural network with the forecast error of proposed algorithm.The accuracy of the proposed algorithm is verified，which shows that the accuracy has been improved.

least squares support vector machine；electricity consumptionforecasting；month-season ratio；Elman neural network

2016-09-03。

杨 柳（1968—），男，大学本科，高级工程师，主要从事电力系统规划分析与研究工作。

（编辑 张晓娟）

国家自然科学基金项目（51507141）。

Project Supported by the National Natural Science Foundation of China（51507141）.

1674-3814（2017）03-0071-06

TM715

A