基于拟合优度检验的连杆疲劳可靠性分析
2017-05-24郝晨光王勇周宇昊
郝晨光,王勇,周宇昊
(1.神华神东电力有限责任公司,北京100033;2.华电电力科学研究院国家能源分布式能源技术(实验)中心,浙江杭州310030)
基于拟合优度检验的连杆疲劳可靠性分析
郝晨光1,王勇2,周宇昊2
(1.神华神东电力有限责任公司,北京100033;2.华电电力科学研究院国家能源分布式能源技术(实验)中心,浙江杭州310030)
在分析常见分布适用范围的基础上,对连杆疲劳寿命采用极大似然法拟合分布参数,通过K-S假设检验和相关性分析对参数模型进行优度检验,得出了适于连杆疲劳寿命可靠性分析的通用性分布模型。在该模型的基础上分析了连杆的可靠度、可靠度寿命和平均寿命,得出了该型连杆的B10寿命。建立了连杆疲劳可靠性分析的流程与方法,评估了连杆的可靠度寿命,对连杆的可靠性使用具有重要意义。
连杆;疲劳;可靠度;拟合优度;K-S检验;可靠度寿命
0 引言
寿命是连杆疲劳可靠性的一个重要指标,且服从一定的统计分布,如果能够确定疲劳寿命服从分布,试验数据的处理就变得简单易行,然而通过试验直接获得的数据往往是杂乱无章,很难直接判断其服从的分布类型。可靠性是产品在规定时间内和规定条件下完成规定功能的能力。可靠性定量分析是对产品进行可靠性分析的重要环节,是通过各种可靠性数据分析工作来完成的。通过可靠性分析可以发现产品的可靠性薄弱环节,改进设计,提高产品的质量与可靠性,在可靠性工程中具有重要地位。
龚文超等人采用参数相关性分析的方法建立了确定寿命分布类型的模型,通过数据处理与仿真计算,验证了产品寿命的分布类型[1]。张姣等人采用M ATLA B程序进行了分布参数估计,实现了参数的极大似然估计[2]。刘峰等人提出了比较分布函数拟合的“相关指数”的方法来优选分布类型[3]。洪延姬等考虑到工程实际中客观存在的相关失效问题,提出了寿命服从威布尔分布产品的相关失效数值分析方法[4]。M ann假定产品失效数据服从威布尔分布,研究了产品到达一定工作时间的可靠度估算方法,用以确定即将投产的产品的保修时间[5]。
某批次连杆在249.39bar载荷下的疲劳试验数据见表1。
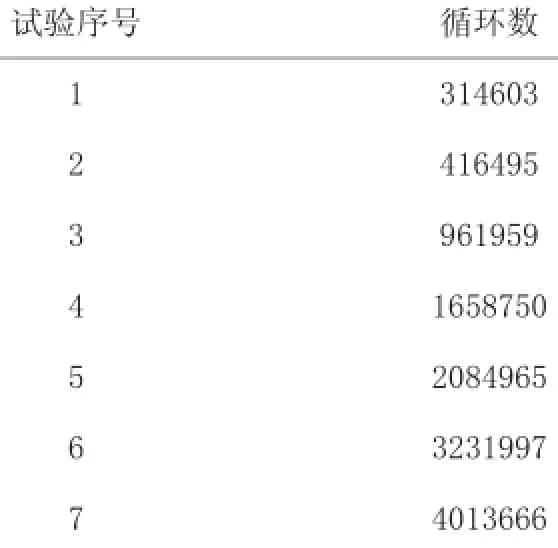
表1 某批次连杆疲劳试验数据
1 产品寿命分布类型
常见的寿命分布类型有威布尔分布、对数正态分布等。
1.1 威布尔分布
威布尔分布是可靠性分析中使用最为广泛的一种分布。大量实践证明,凡是零部件疲劳失效的寿命分布都服从威布尔分布[6,7],鉴于连杆存在最小疲劳寿命,本文采用两参数威布尔分布描述零部件的疲劳寿命,其失效概率密度函数为:

累积失效概率F(t)为:

式中t—时间步数;
β>0—形状参数;
η>0—尺度参数。
1.2 对数正态分布
1947年5月和6月,在全国一些地方大学生掀起“反内战、反饥饿”运动的影响下,湖南大学学生在长沙市举行声势浩大的罢课示威游行。汤甲真不仅自己积极参加,还广泛宣传发动其他同学踊跃参加,痛恨反动统治,更加拥护中国共产党。
对数正态分布是正态分布的一种变形,指产品的寿命对数服从正态分布,由于产品正态分布具有正负无穷寿命,对于产品来说,不可能出现负值寿命,因此使用对数正态分布在工程实际更具合理性。对数正态分布常用来描述金属疲劳、大部分机械结构件等产品的寿命,其失效概率密度函数为:

累积失效概率F(t)为:

式中t—循环次数;
σ—方差;
μ—疲劳指数。
2 数据分析流程
试验中直接获得的数据往往是杂乱无章的,不能直接用于分析计算,进行判断,通过统计学知识对试验数据进行整理、分析后可以使数据显示出一定的规律性,数据分布模型及可靠性分析流程如图1所示。

图1 数据分析流程
3 估计分布参数的数学模型
估计分布参数的方法有很多,相比之下,通过极大似然法得出的估计量性质优良,且适用于各种截尾子样,本文采用极大似然法进行参数估计。
设分布概率密度为f(N,θ1θ2...),累积概率为F(N,θ1θ2...),其中为待估计的分布参数,将数据按从小到大的顺序重新排列,按照顺序统计量的理论,这些子样同时出现的概率为:

取似然函数:其中t为循环次数,θ为循环变量,n为变量个数。
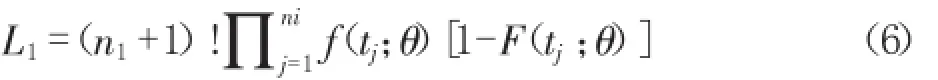
L1为拟合概率,对于K个系统,由于数据之间是相互独立的,因此所有数据的似然函数为;

对于K个系统,使Lk达到最大值的值就是所求的分布参数的估计值,分布参数估计值见表2。

表2 分布参数估计
4 K-S(K olm ogorow-S m irnov)检验
K-S检验是检验单一样本是否来自某一特定分布的方法,以样本数据的累计频数分布与特定理论分布比较。当两者间的差距很小时,则推论该样本属于特定分布族。K-S检验直接把原始数据进行检验,对数据的应用比较完整,检验公式为:
D=m ax Fn(x)-F0(x)(8)
F0(x)表示理论分布的分布函数,Fn(x)表示一组随机样本的累计频率函数,当实际观测D>D(n,alpha)(D(n,alpha)是显著水平为alpha样本容量为n时,D的拒绝临界值)则拒绝H0,反之则接受H0假设,当alpha为0.05时,检验结果见表3。
由表3可知,对数正态分布和威布尔分布均适用于连杆疲劳试验数据。

表3 K-S检验结果
5 拟合优度检验
首先假定数据遵循某种分布类型,估计出分布参数,计算累积失效概率,分析数据遵循所假设分布的高低程度,可以用相关指数R进行衡量:
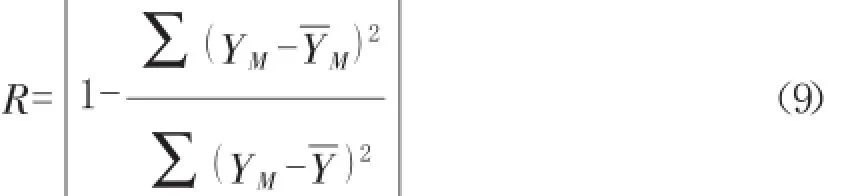
其中YM计算公式为:

(M=1,2,...,N,其中N为故障总数)
Y=∑YM/N(11)其中拟合值YM是拟合编值,N为故障总数,由试验数据求得分布函数的对应值,拟合优度检验结果见表4。

表4 拟合优度检验结果
R值越接近1,说明曲线拟合得越好,即数据遵循所假设分布的程度越高,由表4可知,威布尔分布对连杆疲劳寿命数据更具适用性和代表性,分布函数曲线如图2所示。

图2 分布函数曲线
6 可靠度
可靠度是产品在规定的条件下和规定的时间内,完成规定功能的概率,记为R。用随机变量N表示产品从开始工作到发生疲劳失效的时间。当产品的疲劳寿命服从两参数W eibull分布时,该产品在循环数N时刻的可靠度表达式为,可靠度如图3所示。

β>0为形状参数,η>0为尺度参数。

图3 可靠度曲线
7 平均寿命
平均寿命是产品寿命的平均值,表示连杆工作无故障的循环次数N的数学期望。连杆疲劳寿命服从W eibull分布时,其平均寿命为:

式中Γ(t)—G am m a分布,统计特征值见表5。

表5 统计特征值
8 可靠度寿命
一般情况下,连杆可靠度随着使用循环数的增大而下降,连杆的可靠度等于给定值R(0<R<1)的循环次数,称为可靠度寿命,可靠度寿命表达式为:

可靠度寿命分析如图4所示,Bq为可靠性寿命,寿命见表6。

表6 Bq寿命参数
9 结语
(1)在连杆疲劳试验数据的基础上建立了可靠性分析的模型,在该模型的基础上分析了连杆的可靠性及可靠性寿命,得出了该型连杆的平均寿命为1510400次循环,B 10寿命为377180次循环。
(2)正态分布和威布尔分布均适用于连杆疲劳试验数据。
(3)下一步应结合发动机路谱分析发动机可安全运行的里程数。

图4 可靠度寿命曲线
[1]龚文超,杜毅,伍治海,等.基于参数相关性分析的产品寿命分布类型确定[J].舰船电子工程,2015,35(1):135-138.
[2]张娇,李永红.应用M A TLAB进行寿命数据分析[J].机械工程与自动化,2010,12(3):73-75.
[3]刘峰,何真.机械可靠性数据处理中优选分布类型的探讨[J].机械设计与制造,1998,34(6):3-5.
[4]洪延姬,王志魁,李俊美,等.寿命服从威布尔产品相关失效数值分析[J].装备指挥技术学院学报,2002,13(5):33-35.
[5]M ann N R.W arranty periods based on three ordered sam ple observations from a weibull population[J].IEEE Transactions on R eliability, 1970,19(4):167-171.
[6]W A N I.M.F,GA N D H I.O.P.D evelopm ent of m aintainability for m echanical system[J].R eliability Engineer and System Safety,1999, 65(3):259-270.
[7]Corneliu-A lexandru Slavila,Christophe and M ichel Ferney.Fuzzy A pproach for M aintainability Evaluation in the D esign Process[J].Concurrent Engineering Research and A pplications,2005,3(4):291-300.
Fatigue Reliability Analysis of Connecting Rod Based on Goodness of Fit Test
HAO Chen-guang1,WANG Yong2,ZHOU Yu-hao2
(1.Shenhua Shendong Electric Power Co.,Ltd,Beijing 100033,China;2.Huadian Electric Power Research Institute,The National Energy Distributed Energy Technologies Center,Hangzhou 310030,China)
Based on the analysis ofthe com m on distribution scope,on the basis ofthe fatigue life ofconnecting rod using the m axim um likelihood m ethod fitting distribution param eters,through the K-S hypothesis test,we testwas carried outon the param eterm odeland correlation analysis,obtained the suitable forreliability analysisofgeneraldistribution m odel ofconnecting rod fatigue life.In the m odel,on the basis ofanalyzing the reliability ofconnecting rod life expectancy and life expectancy,reliability,it is concluded that the type of B 10 life of connecting rod.The establishm ent of a connecting rod fatigue reliability analysisofthe processand m ethod,assessed the reliability ofconnecting rod life,use ofthe reliability ofthe connecting rod isofgreatsignificance.
connecting rod;fatigue;reliability;goodness of fit;K-S inspection;reliability life
TK 403
B
2095-3429(2017)02-0012-04
2017-02-26
修回日期:2017-03-24
郝晨光(1982-),男,内蒙古丰镇市人,本科,工程师,研究方向:燃机可靠性分析。
D O I:10.3969/J.ISSN.2095-3429.2017.02.003
