基于随机森林算法的台区合理线损率估计方法
2017-05-23王守相
王守相 ,周 凯 ,苏 运
(1.天津大学 智能电网教育部重点实验室,天津 300072;2.国网上海市电力公司,上海 200122)
0 引言
线损率在评价电力系统的经济运行中扮演着重要的角色,线损管理是电力公司的重点管理内容之一。目前我国线损管理采用《线损四分管理标准》,根据“分压、分区、分线、分台区”的原则对线损进行全面管理。根据国家电网的测算,380 V低压电网的损耗量占总损耗量的1/5,是一个重损层[1]。而低压电网的线损管理普遍采用分台区的管理手段,所以研究台区线损情况、分析影响台区线损的重要因素对提高配电网的经济运行水平具有重要的意义。
从上海电力公司提供的线损系统数据发现,线损系统中数据质量问题表现在数据缺失上,其中供电量数据缺失是导致线损率缺失的主要因素(占台区总数的60%左右)。数据缺失的原因有:供电侧无测点,即没有表计;供电侧数据缺失,即通信问题。另一个主要问题是营销抄表日期冲突,导致线损率不合理。因此,为了充分研究台区线损情况,加强线损管理水平,首要任务是提高线损数据的完整性。随着智能电网建设的推进和智能电表的普及,电力公司积累了大量的电网和用户的历史数据,使充分分析台区线损情况、利用多个数据源对台区线损率进行估计成为可能。
配电网线损计算的方法主要有传统方法、潮流计算方法、人工神经网络算法等。传统方法基于一系列假设对电网进行等值简化,如平均电流法、等值电阻法。为了克服传统方法假设简单的缺点,学者们提出了一些改进的方法,如文献[2]改进了负荷曲线形状系数、铜损、小(多)电源和支路功率的计算;文献[3]通过引入平均电流损耗时间的概念弱化假设条件,以提高计算精度;文献[4]采用了最邻近聚类技术,能快速得出理论线损。潮流计算方法主要是根据潮流计算的结果确定线损,但这类方法需要足够的电网数据、对负荷曲线进行估计和大量的计算,虽然针对此缺点提出了匹配潮流法[5]、改进迭代法[6]、区间算法[7]等解决措施,但对于复杂配电网的可操作性仍较低。基于人工神经网络的线损计算方法的研究很多,人工神经网络往往和其他智能算法相结合对线损进行估计,如遗传算法[8]、免疫遗传算法[9]、动态聚类算法[10]等,这些算法的作用往往是给神经网络选参,但是人工神经网络仍然存在收敛速度慢、参数选择难的问题。为了克服人工神经网络的不足,文献[11]提出了一种基于核心向量机的线损计算方法,文献[12]提出了一种基于快速独立成分分析和支持向量回归的计算方法。智能算法的一个不可避免的问题是特征的选择,而特征多为有功功率、无功功率、线路长度、配电变压器容量等,没有综合考虑用户的特征对线损的影响。另外,对于配电网线损计算的研究多为线路线损,对台区线损的研究较少。由于低压台区数量众多、线路复杂、元件繁多,给线损计算带来很大困难,而基于潮流计算的方法也不现实。目前对低压台区的线损计算多为利用平均电流、电流方差[13]、负荷电量[14]等进行近似计算的等值电阻法以及线性回归方法。虽然有文献通过分类负荷曲线叠加确定电流方差,在一定程度上提高了线损的计算精度[15],但效果仍不理想。 文献[16]提出了一种线性回归预测方法,但预测精度还有待提高。
本文提出一种基于层次聚类、决策树和随机森林算法的台区合理线损率估计方法。首先,结合电力公司线损系统、生产管理系统(PMS)、营销系统(CMS)的多源数据,建立台区特征数据库;然后,采用层次聚类算法对台区进行聚类分析,并建立决策树分类模型;最后,对不同类别的台区建立随机森林估计模型,并对模型的性能进行验证和横向比较。
1 层次聚类和随机森林算法
1.1 层次聚类
低压台区的构成复杂、所辖用户数量和种类繁多,在研究台区的线损特性前,有必要对台区进行分类,对不同的类型分别研究。由于没有明确的指标表明台区的类型,所以台区的分类是一个无监督的聚类问题。层次聚类法[17]是一种无监督聚类技术,其基本思想是逐步分解给定的数据集以形成一个类别的层次。不同于K均值聚类、期望最大化聚类等算法,层次聚类算法不存在初始聚类数的选择问题,这也是本文选择层次聚类法的原因。
层次聚类法的核心是距离的判断准则,包括样本间距离和类间距离。
样本间距离是距离判断的基础,对于特征的不同属性,如数值型特征(用连续变量描述)和类别型特征(用离散型变量描述),又有不同的处理方法。
对数值型特征而言,距离判断准则有绝对值距离、欧氏距离、闵可夫斯基距离、切比雪夫距离等,本文选取归一化距离作为数值型特征的距离判断准则,计算式如式(1)所示。
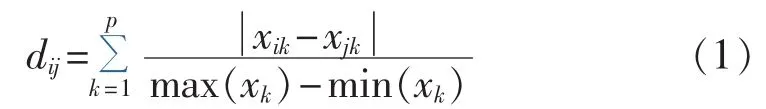
其中,dij为样本i和样本j间的距离;p为特征的维数;k表示第k维特征;xik为样本i第k维特征的值;xk为所有样本的第k维特征的值。
对类别型特征变量采用下述处理方法。对于二元类别型变量,即只能取值0和1的变量,用式(2)计算其样本间距离。

其中,m1为2个样本取值均为1时的变量数目;m2为2个样本取值不同时的变量数目。
对于多元类别型变量,即取值多于2个的变量,首先将其转化成二元类别型变量,然后再按照二元类别型变量的距离计算方法计算其距离。
类间距离的判断准则有最小距离法、最大距离法、中间距离法、类平均法、重心法、离差平方和法。这里选择最大距离法,因为最大距离法能产生更为紧凑的聚类。最大距离法的定义如下:
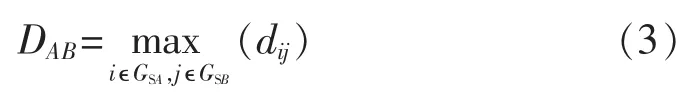
其中,DAB为类A和类B间的距离;GSA表示类A;GSB表示类B。
1.2 聚类效果评价指标
为了评价聚类分析后的效果,本文采用了DBI(Davies-Bouldin Index)指标[18]。 DBI指标计算类内距离与类外距离之比,在整体上衡量聚类的效果。DBI指标值越低,表明聚类效果越好。DBI定义如下:

其中,K为聚类的个数;Rk用于衡量类间的相似度,计算式如式(5)所示。

其中,GA、GB分别用于衡量类A、类B的分散程度;TA为类A中的样本数目;xm为第m个样本;μA、μB分别为类A、类B的中心;MAB用于衡量2个类间的距离。
1.3 随机森林算法
将台区分类后,对不同的类采用随机森林算法[19]建模。随机森林算法是一种集成学习算法,它是一系列的回归树的集合,其输出是所有回归树的预测值的平均值。随机森林算法采用自助重采样技术,克服了回归树的过拟合问题,大幅提高了模型的性能;而且能够处理高维度数据,适用于数值型变量和类别型变量;可以并行化处理,以适应大数据集。随机森林算法的步骤如下:
a.设训练集中预测变量为 X={x1,x2,…,xn},响应变量为 Y={y1,y2,…,yn};
b.对 b=1,2,…,Bs重复步骤 c、d;
c.通过自助重抽样技术从X、Y中随机选择一个子样本集Xb、Yb作为训练集;
d.对Xb、Yb训练一个回归树模型rfb。
训练结束后,对一个新的样本x,随机森林模型通过平均所有回归树的预测值给出该样本的预测值为:
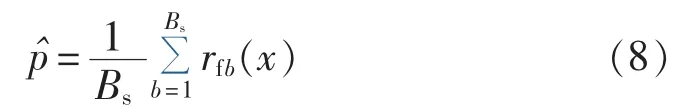
影响随机森林模型性能的主要因素有单棵树的预测强度和树与树之间的相关度。单棵树的预测强度越好,则整体随机森林模型的预测性能越好;树与树之间的相关度越小,则随机森林模型的预测性能越好。这2个因素可以通过每棵树预选的变量个数和树的个数2个参数进行控制。
在回归树的训练中,采用分类回归树CART(Classification And Regression Tree)算法。它是一种二分递归分割的技术,将当前的训练集分成2个子训练集,使得生成的树的每个非叶子节点都有2个分支。非叶子节点代表特征,叶子节点就是树模型给出的预测值。CART算法步骤如下。
a.根据一定条件选择一个特征,根据该特征把树的节点划分为2个分支。
b.在每个分支上递归地重复以上步骤,直到满足以下条件之一:偏差的减少小于给定的界限值;节点中的样本数量小于给定的界限值;树的深度大于一个给定的界限值。
回归树自上而下构建,特征的选择通过计算最好的划分点进行,用节点的不纯度指标 GINI[20]描述,GINI定义如下:

其中,pi为节点中的样本属于类i的概率;M为节点中类的数目。
为了避免回归树过于庞大以及由此带来的过拟合问题,需要对回归树进行剪枝,以剪去对模型贡献不大的分支。剪枝通过复杂度参数cp值进行控制,cp值衡量新增节点后的树对模型拟合优度的提升程度。另外影响回归树性能的重要参数还有节点最小样本数、叶子节点的最小样本数和树的深度等。
2 建模方法和估计方法
对于台区合理线损率估计的研究分成3个部分:台区特征数据库形成部分、模型建立部分和台区线损率估计部分。台区特征数据库形成部分是其他2个部分的基础,模型建立部分的主要目的是建立台区的分类模型和台区线损率的估计模型,而台区线损率估计部分的主要目的是利用估计模型估计数据缺失的台区线损率。
2.1 台区特征数据库形成部分
台区特征数据库形成部分的输入是与台区相关的线损数据、设备台账数据、用户档案数据,输出是台区特征数据。输入数据来源于电力公司的线损系统、PMS和CMS。在数据清洗和预处理阶段,首先在线损系统中提取售电量、线损率、质量码、电系编号等信息,根据电系编号从设备台账中提取台区对应的变压器、设备编号等信息,根据设备编号从用户档案数据中提取台区所辖的用户及其相关信息。对数据中的部分缺失值采用k最邻近算法进行填补,即选择与含有缺失值的样本距离比较接近的n个无缺失值样本,根据这n个样本的平均值或众数填补缺失值。对于台区所辖用户,由于一个台区对应众多用户,因此用“投票”的方式解决一对多的问题。最后得到台区特征。台区特征数据库形成部分的流程图如图1所示。
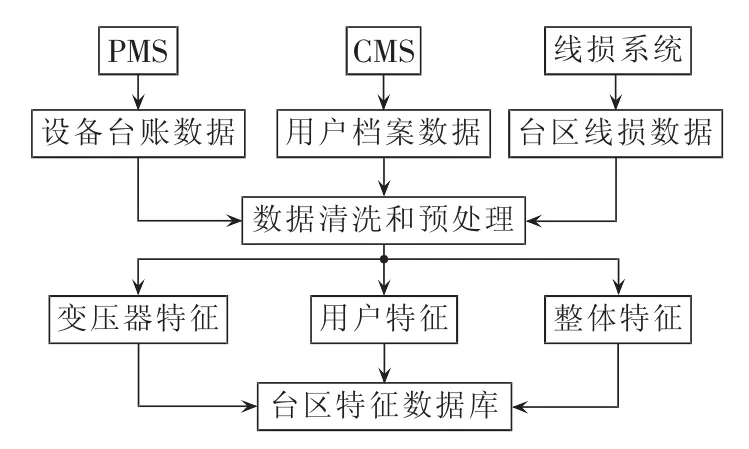
图1 台区特征数据库形成流程图Fig.1 Flowchart of building feature database of transformer district
根据特征的类型,台区特征可以分为三大类:整体特征、变压器特征和用户特征。整体特征从线损系统中直接获取,变压器特征从设备台帐数据中根据台区的电系编号获取,用户特征从用户档案数据中经过一定的处理获得。“用户数”是台区所有用户的数量,以户为单位;“运行(合同)容量总和”是所有用户的运行容量或合同容量的总和;“户平均运行容量”是以上2个特征的商;对于剩下的4个特征,因为每户都有相应的值,所以为了表征台区的特征,采用“投票”的方法处理。以“经济类型”为例,统计某一台区下所有用户的“经济类型”,将频率最高的“经济类型”作为台区的“经济类型”;如果遇到有2种“经济类型”频率相同的情况,则将运行容量大的用户组的“经济类型”作为台区的“经济类型”。
根据数据类型,台区特征可以分为两大类:数值型特征和类别型特征。数值型特征用连续性变量描述,包括线损率、售电量等;类别型特征用离散型变量描述,包括变压器型号、绝缘介质等。台区特征如图2所示。
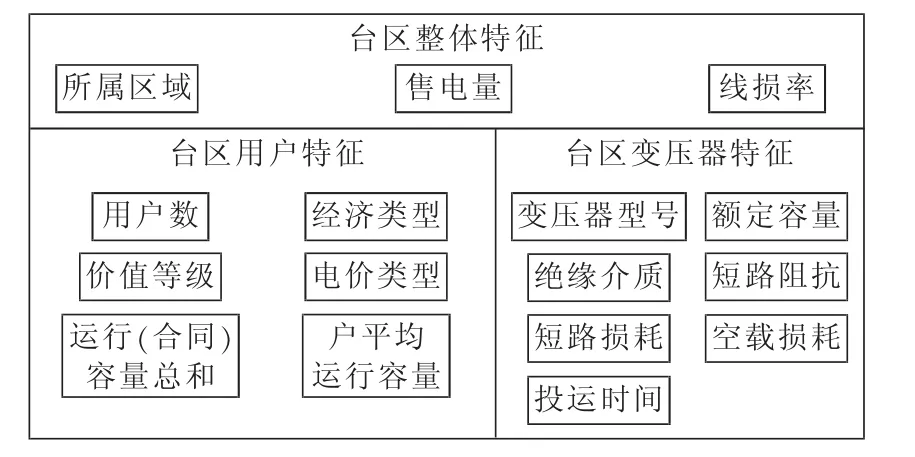
图2 台区特征Fig.2 Features of transformer district
2.2 模型建立部分
模型建立部分的输入是台区特征数据,输出是台区分类模型和台区线损率估计模型。模型建立部分分为三部分:聚类部分、分类模型部分和估计模型部分。
对于聚类部分,首先从台区特征数据库中选择相应的特征,然后利用层次聚类算法进行聚类分析。在台区特征中,对估计线损率而言有些特征是无关和冗余的。“所属区域”特征在台区线损管理中有用,但不同区域的台区线损率并没有呈现不同的分布,因此在建模过程中不考虑“所属区域”特征。“变压器型号”特征是一种类别型特征,其取值达几十种之多,给建模带来了不便;而且,“变压器型号”主要反映了“额定容量”、“绝缘介质”、“短路阻抗”、“短路损耗”和“空载损耗”,因此在其他特征存在的情况下,可以不考虑“变压器型号”特征。利用层次聚类算法进行聚类分析时,将预设的聚类数设置为2,然后分别计算类别数为2~N时的DBI指标,选择DBI最小时对应的类别数作为最终的聚类数。最后标注台区的所属类别。
对已经分好类的台区,利用决策树算法进行分类,建立分类模型,用于台区线损率估计部分。决策树模型是一种树结构,与前文提到的回归树一样采用CART算法训练,区别在于决策树模型预测类别型变量,而回归树模型预测数值型变量。分类模型的性能用错误率指标衡量,错误率指标的计算公式如下:

其中,γerror为模型的错误率;ntotal为总的测试集的样本数量;nerror为分类模型预测的类别与真实的类别不一致的样本数量。
对于估计模型部分,首先根据台区类型选择相应的台区特征输入随机森林算法,算法输出相应台区的随机森林模型,最后给出各类台区的估计模型。估计模型估计的是连续变量,采用平均绝对误差MAE(Mean Absolute Error)和标准化均方误差 NMSE(Normalized Mean Squared Error)指标衡量。
MAE是比较估计值与实际值之间的差距来衡量模型的性能,指标的计算公式如下:
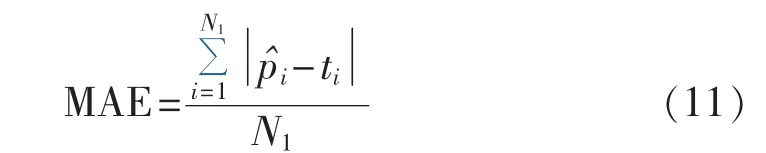
其中,N1为测试集的样本数量;为模型对测试集中样本i的估计值;ti为测试集样本i的真实值。
NMSE指标是比较模型的估计值和训练集的均值,其取值范围通常为0~1。模型的性能越好,NMSE值就越小。指标的计算公式如下:
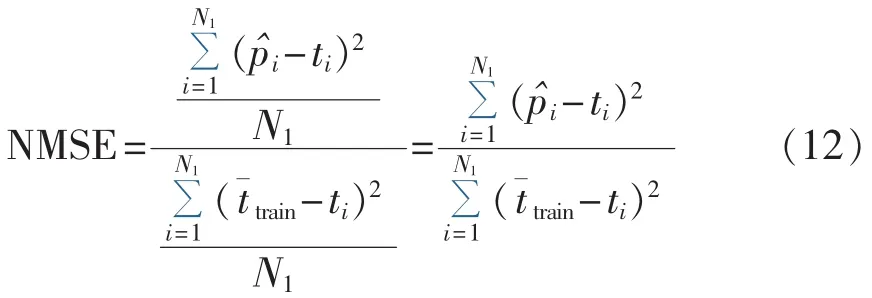
其中为训练集中所有样本的真实值的均值。
本文选择MAE指标的同时选择NMSE指标的原因是:NMSE指标用最简单的模型(即训练集的均值)作为基准,能够有效评价不同模型的性能。
模型建立过程中,采用十折交叉验证的方法估计模型的泛化误差。十折交叉验证是一种常用的测试方法,它将数据集随机等分成10份,用其中的1份作为测试集、其余的9份作为训练集建立模型,将10次模型的性能指标的平均值作为泛化误差的估计。对不同参数的模型分别进行十折交叉验证,选择最小的泛化误差对应下的参数作为模型的最终参数。模型建立部分的流程图如图3所示。
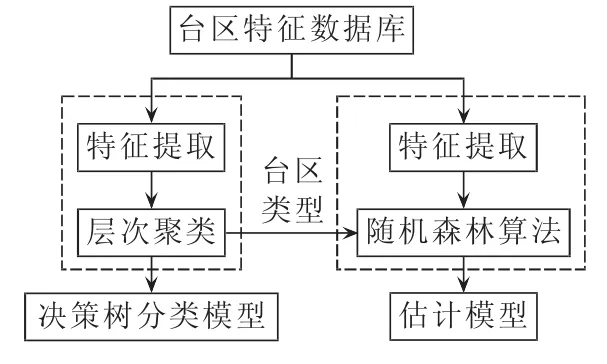
图3 模型建立部分流程图Fig.3 Flowchart of establishing model
2.3 台区线损率估计部分
台区线损率估计部分的输入是待估计台区的特征向量,输出是该台区的线损率。首先从台区特征向量中提取决策树分类模型需要的特征,然后由决策树分类模型得到台区所属的类别。再根据台区类别选择对应的随机森林模型,得到台区线损率。台区线损率估计部分的流程图如图4所示,图中的分类模型对应决策树模型,估计模型对应随机森林模型。此外,可以选择不同的分类模型和估计模型,从而实现不同模型之间的性能比较。
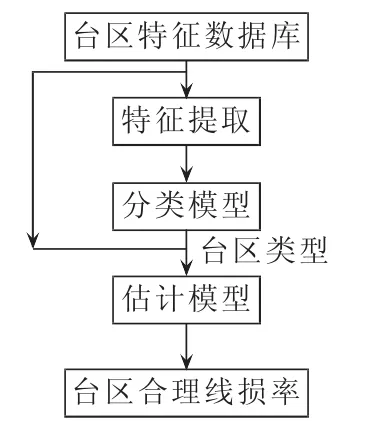
图4 台区线损率估计部分流程图Fig.4 Flowchart of estimating line loss of transformer district
3 实例分析
台区线损相关数据由上海电力公司提供,台区线损率按月统计。空间范围是浦东新区5个地块,用户包括大工业用户、商业用户和居民用户;时间范围是2014年1月至2015年6月。
估计模型的任务是估计台区线损率,因此在选择训练集时选择线损系统中线损率质量码没问题的台区。由于数据的时间跨度为1.5 a,各个台区的月线损率有小范围的波动,因此将各月的线损率的均值作为台区线损率,将各月的售电量的均值作为台区的售电量特征,然后建立台区特征数据库。然而不是所有台区的各月数据都完整,因此将缺失月份超过5个月的台区删除,最后数据库中有943个完整的台区数据。
台区特征数据库建好之后,根据模型建立部分的流程进行聚类分析。首先根据第2节所提方法选择需要的台区特征,然后进行聚类分析。将计算的聚类数NC设为2~9,因为如果NC>9,则至少有一类的台区数量小于94,而过少的数据将会降低模型的估计性能。分别计算每种聚类数情况下的DBI指标,如图5所示。从图5中可以看出,最优的聚类结果是聚类数为5。此时各类中的台区数量如表1所示。从表1中发现:类1和类4的台区数目过少;类1和类2的距离相对较近,类3和类4的距离相对较近,所以不妨将类1和类2合并为一类,将类3和类4合并为一类。所以,最终将台区分成3类,3类台区的聚类中心的标准化值如图6所示。
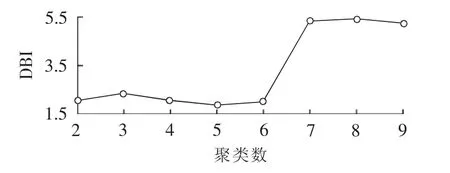
图5 不同聚类数下的DBI值Fig.5 DBI values with different cluster numbers
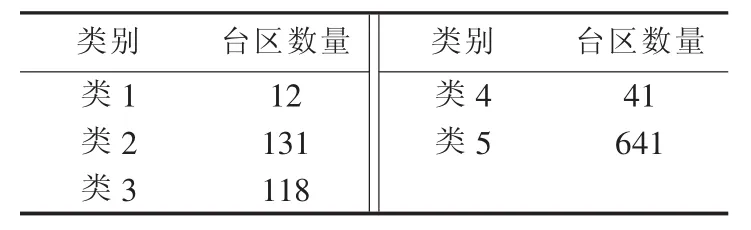
表1 聚类分析结果Table 1 Result of cluster analysis
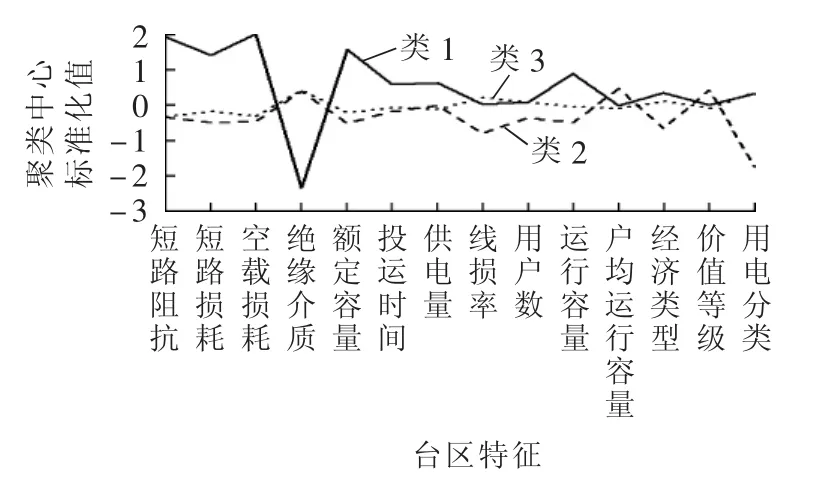
图6 3类台区聚类中心的标准化值Fig.6 Standardized values of three transformer district’s cluster centers
在建模之前,采用分层随机抽样的方法选取10%的台区(94个)用于模型测试,其余的台区用于模型训练。根据训练集建立决策树分类模型,并对每一类台区分别建立估计模型。建模过程中采用上文所述十折交叉验证的方法选择模型的参数。
在建立决策树分类模型过程中,重要的参数是cp值,为了得到尽可能优的参数值,选取不同的cp值分别建立模型,并计算不同cp值下的模型在测试集中的表现,即用分类错误率评价分类模型的优劣。不同cp值下模型的错误率如图7所示。从图7中可以看出cp值为0.03时模型的分类性能最好。最后得到的分类模型参数如下:节点所含最小样本数为20,叶子节点所含最小样本数为7,cp值为0.03,测试集平均错误率为0.0213。
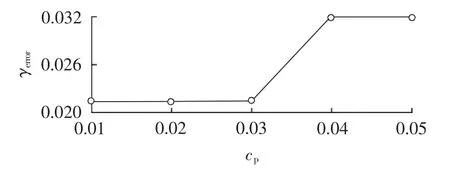
图7 不同cp值时决策树分类模型的错误率Fig.7 Error rates of decision tree classification model with different cpvalues
在建立随机森林估计模型时,重要的参数是节点的变量数和树的个数。首先选择节点的变量数,即在其他参数固定的情况下计算不同节点变量数时模型的NMSE指标。然后采用同样的方法选择树的个数,此时变量数选择最优值,并将其他参数固定。不同参数下模型的性能如图8所示。由图8得到最优模型的参数如表2所示。
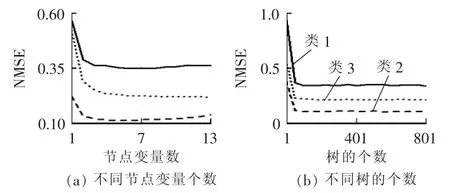
图8 不同参数下随机森林模型的性能Fig.8 Performance of random forest model with different parameters
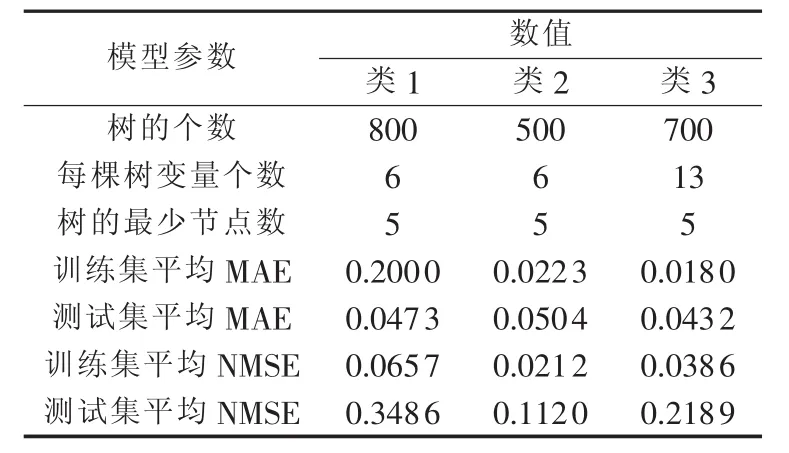
表2 随机森林模型参数及性能Table 2 Parameters and performance of random forest model
选择好参数后,将所有的训练集数据用于训练,建立最终的分类模型和估计模型。然后,根据估计流程将测试集输入估计模型中,得到94个台区线损率的估计值,然后计算模型的性能指标。
为了与其他模型比较,建立了多元线性回归模型、回归树模型和随机森林模型。此外,对于人工神经网络算法,由于其难以处理类别型特征,所以没有考虑用该算法建模。下面对实验结果进行分析。
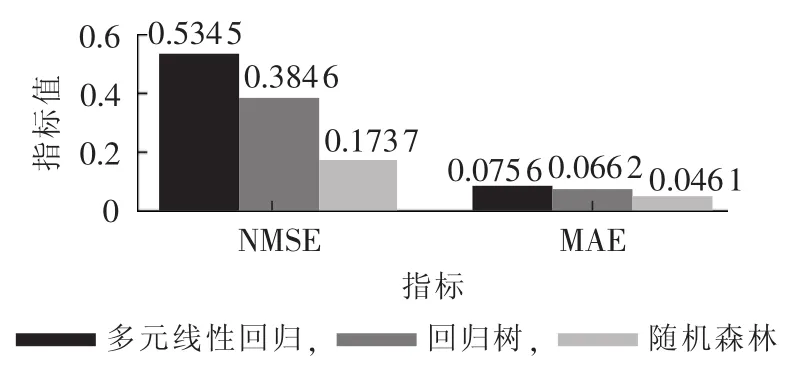
图9 不同模型的性能比较Fig.9 Performance comparison among three models
各个模型的MAE和NMSE指标如图9所示,从图9中可以看出,随机森林模型的性能最好。对于线性回归模型,其依赖正态性、独立性、线性和同方差性的假设。对于台区而言,独立性的假设能够满足,但正态性、线性和同方差性的假设很难满足。如对台区线损率进行Shapiro-Wilk正态分布检验,统计量W的值为0.9821,p值为2.302×10-9,明显小于显著性水平0.05,表明台区线损率不满足正态性假设。这是导致线性回归模型估计性能较差的原因之一。对于回归树模型,虽然其具有解释性、鲁棒性好等优点,但也存在容易过拟合、精确性低的缺点。尤其是树的深度大时,由于其低偏差、高方差的特点,总会过度拟合训练集,造成估计性能较差。对于随机森林模型,生成每一棵回归树时,训练集从整个训练集中随机选取,应用的特征也从所有特征中随机选取,每个节点随机选择特征进行分支,这样降低了各棵回归树间的相关性,避免了单棵回归树过拟合带来的问题,提高了估计的准确度。
抽取10个台区,采用上述方法估计其合理线损率,结果如表3所示。对线损系统中标记为“合理”的台区,其线损率多在2%~8%之间。其中,编号为2、379、216、157、519 的台区线损率估计值的绝对误差在±1%以内,可以认为线损率在合理范围内。编号为185、873的台区估计值的绝对误差在±1%以外,认为其实际线损率偏高,从而管理人员可以对这些台区进一步分析线损率偏高的原因,制定相应对策。对系统标记为“不合理”的台区,其线损率为负值、过大值或缺失,该方法可以给出合理线损率的参考值,从而对这些台区的线损情况有初步了解;另外,编号为185的台区的线损率在6%以上,将其列为重点关注对象。
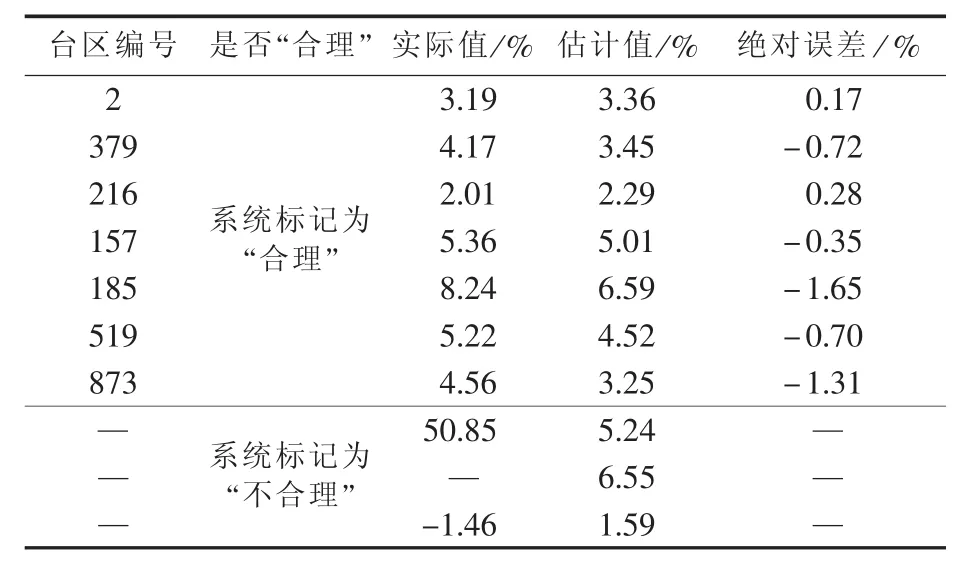
表3 台区合理线损率估计结果Table 3 Estimation results of transformer district line loss rate
4 结论
本文充分利用电力公司线损系统、PMS和CMS的数据,从设备和用户2个角度出发分析台区线损情况,解决了目前对台区线损分析不全面的问题。提出了一种基于层次聚类、决策树和随机森林算法的台区线损率估计模型,克服了采用人工神经网络算法收敛速度慢、难以直接处理离散变量的缺点;并与线性回归模型、回归树模型的估计结果进行了比较,表明所建模型性能优越。本文所提方法可以很好地解决线损系统中供电量缺失和营销抄表日期冲突等造成的台区线损数据缺失问题,为充分研究台区线损情况提供了保障;而且在不增加表计的情况下提高了线损精细化管理程度,从而减小了电网投资,提高了电网的经济效益。
参考文献:
[1]余卫国,熊幼京,周新风,等.电力网技术线损分析及降损对策[J]. 电网技术,2006,30(18):54-57,63.YU Weiguo,XIONG Youjing,ZHOU Xinfeng,et al.Analysis on technical line losses of power grids and counter measures to reduce line losses[J].Power System Technology,2006,30(18):54-57,63.
[2]丁心海,罗毅芳,刘巍,等.改进配电网线损计算方法的几点建议[J]. 电力系统自动化,2001,25(13):57-60.DING Xinhai,LUO Yifang,LIU Wei,et al.Proposals on improving the current methods for calculation of distribution network [J].Automation of Electric Power Systems,2001,25(13):57-60.
[3]付学谦,陈皓勇.平均电流损耗时间法在配网线损计算中的应用[J]. 电工技术学报,2015,30(12):377-382.FU Xueqian,CHEN Haoyong.Energy losses estimation using equivalent time of average current[J].Transactions of China Electrotechnical Society,2015,30(12):377-382.
[4]李滨,杜孟远,韦维,等.基于准实时数据的智能配电线损计算[J]. 电力自动化设备,2014,34(11):122-128,148.LI Bin,DU Mengyuan,WEI Wei,et al.Calculation of theoretical line loss based on quasi real-time data of smart distribution network[J].Electric Power Automation Equipment,2014,34(11):122-128,148.
[5]李学平,刘怡然,卢志刚,等.基于聚类的阶段理论线损快速计算与分析[J]. 电工技术学报,2015,30(12):367-376.LI Xueping,LIU Yiran,LU Zhigang,et al.Phase theoretical line loss calculation and analysis based on clustering theory[J].Transactions of China Electrotechnical Society,2015,30(12):367-376.
[6]欧阳森,冯天瑞,安晓华.考虑馈线聚类特性的中压配网线损率测算模型[J]. 电力自动化设备,2016,36(9):33-39.OUYANG Sen,FENG Tianrui,AN Xiaohua.Line loss rate calculation model considering feeder clustering features for medium voltage distribution network[J].Electric Power Automation Equipment,2016,36(9):33-39.
[7]陈得治,郭志忠.基于负荷获取和匹配潮流方法的配电网理论线损计算[J]. 电网技术,2005,29(1):80-84.CHEN Dezhi,GUO Zhizhong.Distribution system theoretical line loss calculation based on load obtaining and matching power flow[J].Power System Technology,2005,29(1):80-84.
[8]丁心海,罗毅芳,刘巍,等.配电网线损理论计算的实用方法——改进迭代法[J]. 电网技术,2000,33(1):39-42.DING Xinhai,LUO Yifang,LIU Wei,etal.A new practical method for calculating line loss of distribution network-improved iteration method[J].Power System Technology,2000,33(1):39-42.
[9]王成山,刘姝,林勇.基于区间算法的配电网线损理论计算[J].电力系统自动化,2002,26(2):22-27.WANG Chengshan,LIU Shu,LIN Yong.Electric network loss calculation using interval iteration method[J].Automation of Electric Power Systems,2002,26(2):22-27.
[10]辛开远,杨玉华,陈富.计算配电网线损的GA与BP结合的新方法[J]. 中国电机工程学报,2002,22(2):80-83.XIN Kaiyuan,YANG Yuhua,CHEN Fu.An advanced algorithm based on combination of GA with BP to energy loss of distribution system[J].Proceedings of the CSEE,2002,22(2):80-83.
[11]李秀卿,汪海,许传伟,等.基于免疫遗传算法优化的神经网络配电网网损计算[J]. 电力系统保护与控制,2009,37(11):36-39,49.LIXiuqing,WANG Hai,XU Chuanwei,etal.Calculation of line losses in distribution systems using artificial neural network aided by immune genetic algorithm[J].Power System Protection and Control,2009,37(11):36-39,49.
[12]姜惠兰,安敏,刘晓津,等.基于动态聚类算法径向基函数网络的配电网线损计算[J]. 中国电机工程学报,2005,25(10):35-39.JIANG Huilan,AN Min,LIU Xiaojin,et al.The calculation of energy losses in distribution systems based on RBF network with dynamic clustering algorithm[J].Proceedings of the CSEE,2005,25(10):35-39.
[13]彭宇文,刘克文.基于改进核心向量机的配电网理论线损计算方法[J]. 中国电机工程学报,2011,31(34):120-126.PENG Yuwen,LIU Kewen.A distribution network theoretical line loss calculation method based on improved core vector machine[J].Proceedings of the CSEE,2011,31(34):120-126.
[14]彭建春,李春晖,祁学红,等.基于快速独立成分分析和支持向量回归的混合馈线线损估算[J].电力系统保护与控制,2012,40(3):51-55.PENG Jianchun,LI Chunhui,QI Xuehong,et al.Loss estimation of power distribution systems based on fast independent component analysis and support vector regression[J].Power System Protection and Control,2012,40(3):51-55.
[15]刘庭磊,王韶,张知,等.采用负荷电量计算低压配电台区理论线损的牛拉法[J]. 电力系统保护与控制,2015,43(19):143-148.LIU Tinglei,WANG Shao,ZHANG Zhi,et al.Newton-Raphson method for theoretical line loss calculation of low-voltage distribution transformer district by using the load electrical energy[J].Power System Protection and Control,2015,43 (19):143-148.
[16]邹云峰,梅飞,李悦,等.基于数据挖掘技术的台区合理线损预测模型研究[J]. 电力需求侧管理,2015,17(4):25-29.ZOU Yunfeng,MEI Fei,LI Yue,et al.Prediction model research of reasonable line loss for transformer district based on data mining technology[J].Power Demand Side Management,2015,17(4):25-29.
[17]MURTAGH F,CONTRERAS P.Algorithms for hierarchical clustering:an overview[J].Wiley Interdisciplinary Reviews Data Mining&Knowledge Discovery,2012,2(1):86-97.
[18]DAVIES D L,BOULDIN D W.A cluster separation measure[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2009,PAMI-1(2):224-227.
[19]BREIMAN L.Random forests[J].Machine Learning,2001,5(1):5-32.
[20]STROBL C,BOULESTEIX A L,AUGUSTIN T.Unbiased split selection for classification trees based on the gini index [J].Computational Statistics&Data Analysis,2007,52(1):483-501.
