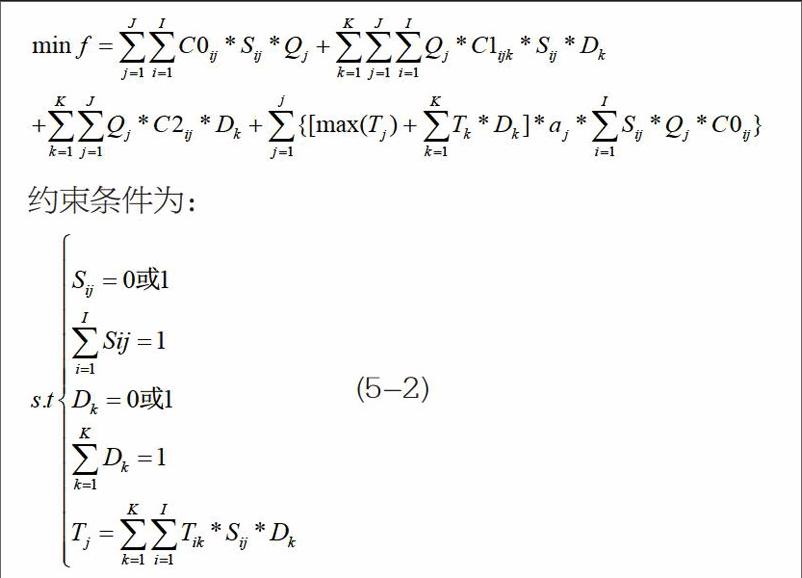基于粒子群算法的易逝品供应物流网络优化

梁瑞伟

在对易逝品的采购与运输规划的过程中，不但要考虑其采购成本，运输成本，而且还要考虑其时间成本。在很多情况下，时间成本甚至是更具决定意义的一个因素。本文依托湖南省教育厅科技处项目（项目编号1lc0926）对一个典型的易逝品采购问题建立了基于粒子群算法的数学模型，并用标准粒子群算法和改进的粒子群算法对其进行了求解，说明了用粒子群算法对该问题的整套解决方案是有效的。

在现实生活中有些物品其价值随着时间的流逝其价值逐渐减少。我们称这类物品为易逝品。像时装、电子元件等，其时效性很强，一段时间后由于新产品的出现使其价值迅速降低；蔬菜、水果、肉类等，对它们进行保鲜不易而且所需要的成本很高高，存在着时间成本。因此在对易逝品的采购与运输规划的过程中，不但要考虑其采购成本，运输成本，而且还要考虑其时间成本。在很多情况下，时间成本甚至是更具决定意义的一个因素。

韩世莲等定义了客户等待时间的含义及目标规划的原理，对带时间窗的多目标物流配送线路优化问题建立了一个线性规划模型。在模型建立时考虑了运输费用最小、运输时间最短和所有客户的等待时间最短三个相互冲突的目标。

王海丽等以带时间窗的车辆配送规划模型为基础，以制冷成本、车辆固定成本和运输成本之和的总成本为目标函数，建立了一个关于易腐食物品的冷藏配送模型。在求解的算法设计上，构造了一个基于邻域搜索的节约算法。

陈军等研究了由于采购联盟间成员信息的不完全与不对称。各成员均将对方的期望需求作为对方的实际需求进行估计。针对易逝品采购与运输的特点，提出了关于调剂价格的特殊约束条件并建立了一个联盟期望利润模型，最后用数值进行了仿真。

王海军等根据应急物流的特点，将模拟退火算法用于应急物流的车辆调度研究之中并通过实例将模拟退火算法和免疫算法进行了比较，证明了用模拟退火算法来优化车辆行驶路径的可行性和全局最优性。

问题提出

在这里考虑一家企业向I家供应商采购J种物料（这些物料为易逝品）经过K个中转站中的某一个集中将物料运送至企业，每种物料的价值以单位时间a_j的速率递减；公司需要确定采购每种物料的供应商以及中转站，以使采购成本、运输成本以及物料价值按时间的损耗成本之和最小。该问题可用穷举法寻找最优方案，需要比较的方案为I^J*K个，其复杂程度与供应商、采购原材料种数呈指数增长，与中转站个数呈倍数增长。

数学建模

在建立该问题的数学模型之前。基于粒子群算法的特征，为方便建模与优化运算，设定参数和决策变量如下：

CO_ij-企业从供应商i处采购的j种物料的单价；

Q_j-企业需要采购的第j种物料的数量；

Cl_ijk-从供应商i处采购的j种物料运送至中转站k处的运费单价；

C2_jk-从中转k站处将第j种物料运送至企业的运费单价；

T_ik-表示从企业i到中转站j的运输时间，各物料所需时间相同；

T_j-表示将第种物料运送至选定的中转所需的时间；

T_k-物料从中转站k运送至企业所需的时间；

a_j-单位时间内物料价值损失占物料总价值的百分比；

S_ij-表示中物料j是否在供应商处i采购，是则S_ij=1否则S_n=0；

D_k-中转站k是否为本次采购方案选定的中转站是则D_k=1否则D_k=0；

其中下标含义为：i为供应商索引号（u=1，2，…，I），j为企业所需原材料索引号（j=1，2，…，J），k为中转站索引号（k=1，2，…，K）。

在定义了上述参数符号之后，可建立该供应物流网络模型的总成本目标函数。该总成本函数由四部分构成：购成本，第一次运输成本，第二次运输成本，运输时间损耗成本。（忽略中转费用和中转时间）：

约束条件为：

算法设计

在本模型中CO_ij、C1_ijk、C2_jk、T_ik、T_k、Q_j、a_j均为已知变量，T_j为中间变量，只有S_ij和D_k为决策变量，而且S_ij和D_k均为0，1变量，总共有I*J+K个0，1决策变量，且这些决策变量需要满足，这两个约束条件。也就是说这i*j+k个0，1决策变量中可行解必然是含有J+1个1，而其它决策变量均为O。其中前面J个1分别确定每种原材料的供应商，最后一个1确定所选择的中转站。

粒子群算法最初是用于求解连续性优化问题的，对这种0，1型离散性优化问题有对应的二进制粒子群算法来解决。但考虑到本模型中约束的特点，可对连续型粒子群算法稍做变换然后用来求解该问题将会十分便捷。用连续型粒子群算法来优化该问题的具体步骤可如下：初始化，每个粒子为I*J+K维，均取（0，1）之间的随机值，并把它分成J行I列加1行K列的两个矩阵，按此方法同样对速度进行初始化；计算粒子的适应值。对每个粒子先将其每行最大元素置为1，其他元素值为0，让后按照式（5.1）计算出其适应值；找出每个粒子历史最优与群体最优粒子；更新粒子位置；更新粒子速度；按照步骤2）计算更新后粒子的适应值，更新粒子历史最优与群体最优；判断是否满足终止条件，是则终止计算输出结果，否则转移到第四步。

该方法主要是在计算粒子最优值时做了一些特殊的处理以使每个粒子均满足约束成为可行解。

实例仿真

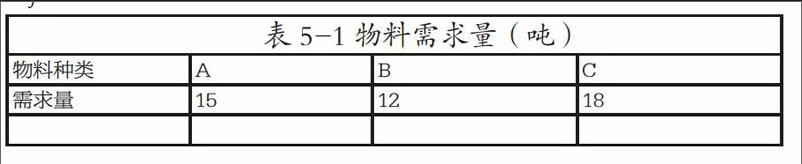
考虑一家电子厂需要从三个供应商S₁、S₂、S₃中采购三种电子元件A、B、C经过三个中转站D₁、D₂、D₃中的某个中转站中转然后集中将物料运送至工厂E。其中物料随时间损耗比率为a_j=0.25%/天其它相关数据如表5-1——表5-4所示：

公司需要制定一个采购方案从这三家供应商处采购三种原材料并选择合适的中转站以使采购成本、运输成本、时间损耗成本之和最小。本文将用粒子群算法计算上述模型并用matlable语言编写程序，最終解决该问题。在该实例中每个粒子的维数为I*J+K=3*3+3=12设定种群规模为20，迭代代数为500代。用三种粒子群算法计算，通过30次实验，获得收敛到最优解的平均迭代次数如表5-5所示，最优方案方案如表5-6，表5-7所示。

从表5-5中可知，三种粒子群算法均能稳定的收敛到全局最优解，而在30次实验中，两种改进的粒子群算法收敛到最优解的平均迭代次数均比标准粒子群算法所需要的平均迭代次数少，说明改进的粒子群算法在求解该实例中的收敛速度要比标准粒子群算法快。

即A物料选择在供应商三处采购；B物料选择在供应商一处采购；c物料在供应商三处采购，选择中转站二为物料中转集中运输中转站。

该方案采购成本为：652.5（万元）

运输成本为：56，25（万元）

物料随时间的损耗成本为：35.8875（万元）

总成本为：747.6375（万元）

用穷举例法本实例有81种方案，该结果与穷举法获得的最优方案相同。

本文首先提出了易逝品的供应物流网络优化问题，其后基于粒子群算法对该问题建立了各数学模型，最后用粒子群算法来求解了该模型，比较了三种粒子群算法在该实例的收敛速度，并将粒子群算法获得的方案与用穷举法算出的结果进行比较，说明了用粒子群算法对该问题的整套解决方案是有效的。