基于ADAMS仿真及线性回归分析设计大角度转向悬架导向机构
2017-05-19李占玉董铸荣邓志君任少云
李占玉,董铸荣,2,邓志君,任少云
(1.深圳职业技术学院 汽车与交通学院,广东 深圳 518055;2. 北京交通大学 机电控制工程学院,北京100044)
基于ADAMS仿真及线性回归分析设计大角度转向悬架导向机构
李占玉1,董铸荣1,2,邓志君1,任少云1
(1.深圳职业技术学院 汽车与交通学院,广东 深圳 518055;2. 北京交通大学 机电控制工程学院,北京100044)
为四轮驱动四轮独立转向电动汽车设计一款不等长双横臂式独立悬架的导向机构,该悬架导向机构可以实现车轮90°转角。以车轮跳动时车轮横向位移量和车轮外倾角的变化量作为悬架导向机构设计的重点评价因素,在ADAMS仿真软件建立该悬架导向机构模型,并选取若干不同尺寸的导向机构进行仿真试验,获取车轮横向位移量和车轮外倾角变化量的考察样本,利用数据统计分析方法中的数据相关性及线性回归统计分析求得不等长双横臂独立悬架两个横臂长度的最优值。
车辆工程;四轮转向;双横臂悬架;ADAMS;回归分析
电动汽车电机驱动的方式有中置电机驱动、轮毂电机驱动等,根据驱动力的分配又可分为前驱、后驱、四驱等[1]。采用轮毂电机四轮驱动四轮独立转向(4WID-4WIS)的电动轿车是电动汽车发展的一个新方向[2-3]。电动机安装在车轮轮毂内,电机转子为外转子,输出转矩直接传输到车轮,舍弃了传统的离合器、减速器、传动桥、差速器等部件,使整车质量减轻[4]。在转向上,取消传统的转向梯形机构,采用电机控制的线控转向系统,4个车轮都能够进行大角度转向,除了实现传统四轮转向汽车的正向偏转和逆向偏转外,还可以进行车辆的原地转向(即零转弯半径)和横向移动,极大提高汽车的灵活性[5]。为此,需要重新设计悬架的导向机构来迎合4WID-4WIS电动轿车的特点。
如何合理选择悬架导向机构设计参数是悬架设计的一个重要问题,使用计算机辅助寻优技术是解决该问题的一个很好方法[6]。悬架的导向机构决定众多车轮定位参数,所以悬架导向机构的设计是一项非常复杂的内容,侧重不同的评价目标会导致不一样的设计。笔者为4WID-4WIS电动汽车设计了一个不等长双横臂式独立悬架,该悬架导向机构可以实现最大转向角90°。以车轮横向位移量和车轮外倾角的变化量作为设计的重点评价因素,利用ADAMS仿真试验出相关参数,然后利用相关性及线性回归分析计算出符合要求的不等长双横臂独立悬架导向机构。
1 不等长双横臂悬架结构
悬架导向机构可以有多种类型,结合4WID-4WIS汽车的车身参数[7]和车轮要实现90°转角的要求,研究团队经过反复论证,确定选用不等长双横臂式机构[8]。悬架导向机构的方案设计、运动分析借助ADAMS软件来完成。
1.1 不等长双横臂悬架机构
不等长双横臂式独立悬架系统的结构设计如图1。由于车辆尺寸和转向电机的限制,该悬架导向机构受到一定的约束,相关参数约束条件见表1。

图1 不等长双横臂悬架结构Fig. 1 Suspension structure with double lateral arms in unequal length

表1 不等长双横臂悬架导向机构的约束条件
1.2 不等长双横臂悬架导向机构的评价目标
车轮定位参数影响汽车的行驶,而悬架的导向机构决定了车轮的定位参数,所以在设计中侧重不同的评价目标会导致不一样的设计。笔者以车辆行驶中轮胎磨损量为评价目标,为此评价的目标选择车轮跳动时车轮横向位移量ΔL和车轮外倾角的变化量Δσ。根据汽车设计要求,轮胎上跳50 mm时,单轮轮距变化一般不超过±5.0 mm,车轮外倾角变化量在-2°~+0.5°之间[9-10],即-5.0 mm≤ΔL≤+5.0 mm,-2°≤Δσ≤+0.5°。
在该悬架系统中,悬架机构可以简化为如图2的几何模型。图2中:以下横臂与车身的铰接点O为坐标原点,汽车的横向为X轴,汽车的垂直方向为Y轴,建立OXY平面坐标系。那么车轮上下跳动过程中车轮接地中心P在XY平面的坐标为(XP,YP),车轮中心Q在XY平面的坐标(XQ,YQ)。由表1可推算出:汽车静止时车轮着地点的中心P在XY平面的坐标是P0(430,-150),车轮中心Q在XY平面的坐标是Q0(430,70)。
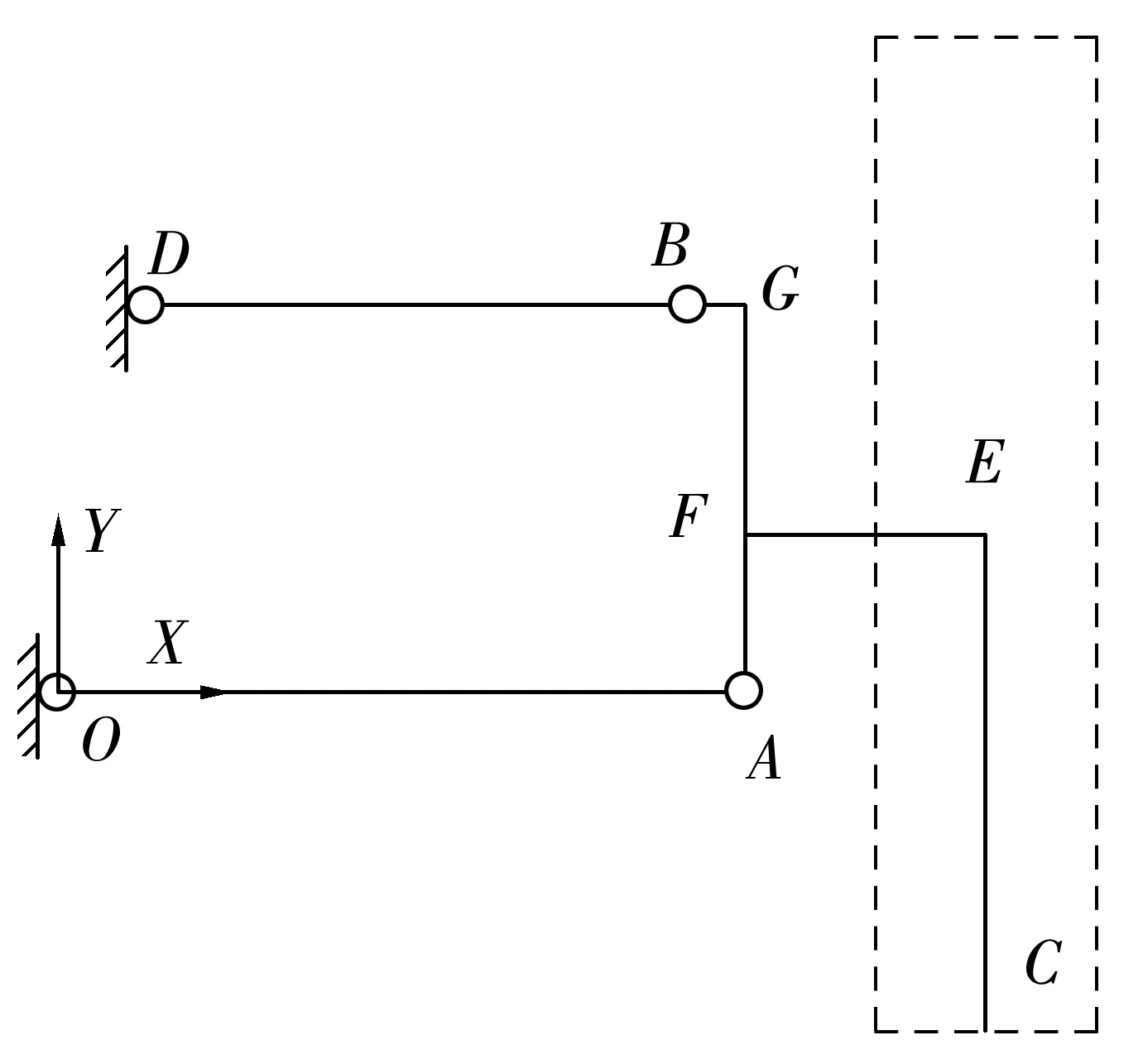
O—下横臂与车身的铰接点;A—下横臂与主销的铰接点;B,D—上横臂两端的铰接点;Q—车轮中心;F—主销中点;P—车轮接地中心点;G—过B点作与主销的垂直线,该垂直线与主销的交点。图2 悬架导向机构几何模型Fig. 2 Geometric model of suspension guide device
由几何关系可以推断出车轮横向位移量ΔL为
ΔL=(XP-430)
(1)
车轮外倾角的变化量Δσ为
Δσ=arctan[(XP-XQ)/(YQ-YP)]
(2)
主销内倾角为
β=arctan[(XA-XB)/(YB-YA)]
(3)
主销的中点纵坐标YF=170,横坐标为
(4)
由于受到转向电机和轮距的限制,在图2的简化模型中A点不能进一步往车轮靠拢,O,D两点位置不能改变,即限制条件为
XA≤330 mm
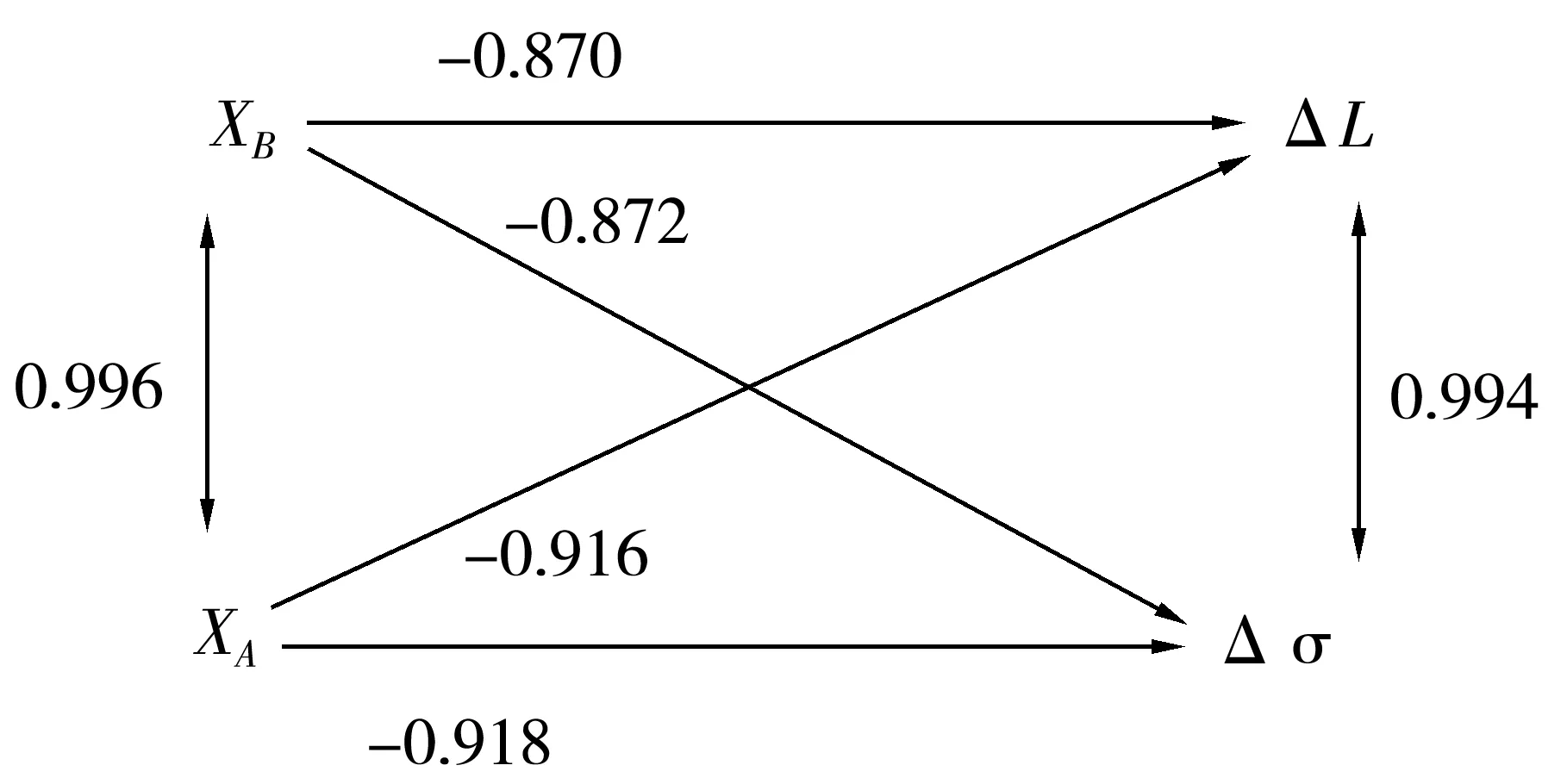
(5)
XD (6) XB+Φ≤XA (7) 式中:Φ为转向电机套筒的半径,由表1的设计参数可以推算出XD=60 mm,Φ=23 mm。 主销内倾角β的范围要求是7°~13°[8-9]。因此,XA,XB的约束条件满足: 计算出约束条件为:83 mm 2.1 不等长双横臂悬架导向机构参数选择 以XB为自变量,XA为应变量。只要满足60 mm 当XA和XB确定后,主销中点F的横坐标XF可以按照式(4)计算,如表3。 表2 不等长双横臂悬架导向机构参数选择 Table 2 Parameters selection of suspension guide device with double lateral arms in unequal length XBXAXB+23XB+28XB+33XB+39.180.00103.00108.00113.00119.10155.00178.00183.00188.00194.10230.00253.00258.00263.00269.10307.00330.00——— 表3 不等长双横臂悬架主销中点横坐标 Table 3 The center of king pin inXaxis of suspension guide device with double lateral arms in unequal length mm XBXAXFXBXAXF80103.0093.53155194.10178.0080108.0096.47230253.00243.5380113.0099.41230258.00246.4780119.10103.00230263.00249.41155178.00168.53230269.10253.00155183.00171.47307330.00320.53155188.00174.41 2.2 仿真分析 在ADAMS中,分别取XB=80,XA=103,XF=93.53,使车轮上跳50mm进行仿真试验。车轮的跳动量即为接地中心P点在Y轴上的变化量,如图3。 图3 车轮的跳动量(YP)曲线Fig. 3 The curve of the volume of wheel jumping (YP) 由图3可知:在约2s后车轮上跳有规律性,最大上跳值在-100 mm,由于车轮静止时YP=-150 mm,所以车轮的跳动量满足50 mm的要求,该次仿真试验2s后的数据可以用于分析。从2s后的数据中取5个最接近-100 mm的上跳值,并结合式(1)和式(2)分析,结果如表4。 表4 XB=80 mm,XA=103 mm时仿真数据分析 由表4可知:当XB=80 mm,XA=103 mm,车轮上跳50 mm过程中,车轮横向位移ΔL=9.06 mm,ΔL方差为0.02,车轮外倾角的变化量Δσ=4.82°,Δσ的方差为0.005 8;由于ΔL的变化量较大,其方差要求为≤0.05;Δσ比较敏感,其方差要求为小于等0.01,可见两者的方差均满足要求。 以相同的方法,对满足表2的其他数值进行仿真,分析车轮横向位移ΔL和车轮外倾角的变化量Δσ,结果如表5。 由表5可见:ΔL方差≤0.05,Δσ方差≤0.01;所以表5中的ΔL和Δσ可信。 表5 ΔL和Δσ取值 3.1 绘制散点图 在SPSS软件中,将XB,XA,ΔL,Δσ等数据导入并绘制散点图,如图4。由图4可知:ΔL与XB,XA呈现负相关;Δσ与XB,XA呈现负相关;ΔL和Δσ为正向相关。 图4 仿真数据散点图Fig. 4 The spot map of simulation data 3.2 相关及回归分析 采用Pearson相关性分析,结果见表6。系数介于1~-1间;ΔL和Δσ的Pearson相关系数为0.994,为高度正相关,即两者有同时增高或降低的趋势;ΔL与XB,XA相关系数均在-0.87和-0.872,为高度负相关,当XB,XA增高时,ΔL在减小;Δσ与XB,XA相关系数均在-0.916和-0.918,为高度负相关,当XB,XA增高时,ΔL在减小。 表6 仿真数据相关性 注:**表示在0.01 水平(双侧)上显著相关。 3.3 回归分析 3.3.1XB对ΔL的回归分析 模型为有意义的F=34.113,P<0.001,R=0.756,XB能解释ΔL=75.6%的变异量。 方程为:ΔL=-0.061XB+11.767,标准方程为:ΔL=-0.870XB。 3.3.2XA对ΔL的回归分析 模型是有意义的F=34.761,P<0.001,R=0.760,XA能解释ΔL=76.0%的变异量。 方程为:ΔL=-0.062XA+13.799,标准方程为:ΔL=-0.872XA。 3.3.3XB对Δσ的回归分析 模型是有意义的F=57.094,P<0.001,R=0.838,XB能解释Δσ=83.8%的变异量。 方程为:Δσ=-0.022XB+5.983,标准方程为:ΔL=-0.916XB。 3.3.4XA对Δσ的回归分析 模型是有意义的F=58.762,P<0.001,R=0.842,XA能解释Δσ=84.2%的变异量。 方程为:Δσ=-0.023XA+6.727,标准方程为:ΔL=-0.918XA。 3.3.5 相关和回归模型 将XB,XA,ΔL,Δσ间的相关系数和标准回归系数绘制在路径图上,如图5。 图5 XB,XA,ΔL,Δσ间相关和回归系数模型 Fig. 5 The model of relevance and regression parameters amongXB,XA,ΔL,Δσ 由相关和回归分析可见:Δσ,ΔL由XB,XA进行解释和预测是合理可行的,XB,XA增大的同时,Δσ,ΔL在单调降低,且Δσ和ΔL接近完全线性正相关,Δσ和ΔL同时增高或降低。 由此可得出结论:对本悬架,当XB=307 mm,XA=330 mm 时,车轮横向位移量ΔL和车轮外倾角的变化量Δσ能同时达到最优,即ΔL=-2.59 mm,Δσ=0.41°,满足汽车设计要求。因此,本悬架最优参数为:上横臂247 mm,下横臂330 mm,轮毂电机轴与下横臂距离70 mm,车轮中心与主销的距离100 mm,主销的长度170 mm。 [1] 钱立军,赵韩,高立新.电动汽车开发的关键技术及技术路线[J].合肥工业大学学报(自然科学版),2002,25(1):14-18. QIAN Lijun, ZHAO Han, GAO Lixin. On the key technologies and technology route of electric vehicle development[J].JournalofHefeiUniversityofTechnology(NaturalScienceEdition), 2002, 25(1): 14-18. [2] 董铸荣,梁松峰,田超贺.一种电动汽车轮毂电机再生制动试验台架的设计与实现[J].汽车技术,2012(8):54-56. DONG Zhurong, LIANG Songfeng, TIAN Chaohe. The design and realization of test-bed for regenerative braking experiment of hub-motor for EV[J].AutomobileTechnology, 2012(8): 54-56. [3] 邓志君,董铸荣.基于垂向性能研究的新型悬架参数设计[J].机械设计与制造,2012(8):37-39. DENG Zhijun, DONG Zhurong. Parameter design of novel suspension based on the research on vertical performance[J].MachineryDesign&Manufacture, 2012(8): 37-39. [4] 董铸荣,贺萍,梁松峰,等.基于再生制动的四轮毂电机独立驱动电动汽车差速转向控制研究[J].汽车技术,2013(5):18-21. DONG Zhurong, HE Ping, LIANG Songfeng, et al. Research on differential steering control of four-hub motor driven electric vehicle based on regenerative braking[J].AutomobileTechnology, 2013(5): 18-21. [5] 邓志君,董铸荣.线控全方位转向四轮驱动电动汽车的独立悬架[J].机械设计,2011(2):77-80. DENG Zhijun, DONG Zhurong. Independent suspension of a wire controlled omni-directional steering four-wheel driven electric car[J].JournalofMachineDesign, 2011(2): 77-80. [6] 潘云伟,胡启国,罗天洪,等.基于遗传算法的悬架系统的优化和仿真[J].重庆交通大学学报(自然科学版),2013,32(5):1068-1070. PAN Yunwei, HU Qiguo, LUO Tianhong, et al. Simulation and optimization of suspension system based on genetic algorithm[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2013, 32(5): 1068-1070. [7] 梁松峰,董铸荣,邱浩.基于死区逆变换补偿的纯电动转向系统控制方法设计[J].重庆交通大学学报(自然科学版),2014,33(3):145-148. LIANG Songfeng, DONG Zhurong, QIU Hao. Control method for electric power steering system based on dead-zone inverse transforming compensation[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2014, 33(3): 145-148. [8] 邓志君,董铸荣,马德粮.电动轿车独立转向轮悬架设计[J].汽车技术,2010(12):37-41. DENG Zhijun, DONG Zhurong, MA Deliang. Suspension design of the independent steering wheel for electric car[J].AutomobileTechnology, 2010(12): 37-41. [9] 过学迅.汽车设计[M].北京:人民交通出版社,2005. GUO Xuexun.AutomobileDesign[M].Beijing:China Communications Press, 2005. [10] 汽车工程手册编辑委员会.汽车工程手册(设计篇)[M].北京:人民交通出版社,2001. Automotive Engineering Handbook Editorial Board.AutomotiveEngineeringHandbook(Design)[M].Beijing:China Communicat-ions Press, 2001. (责任编辑:刘 韬) Design of Steering Suspension Guide Device with Large Angle Based on ADAMS Simulation and Linear Regression Analysis LI Zhanyu1, DONG Zhurong1, 2, DENG Zhijun1, REN Shaoyun1 (1.School of Automotive and Transportation Engineering, Shenzhen Polytechnic, Shenzhen 518055, Guangdong, P. R. China;2.School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, P. R. China) A double lateral arms independent suspension guide device was designed for 4WID-4WIS electric vehicle (electric vehicle with four wheels driven and independent steering of four wheels), whose arms were with unequal length. The proposed suspension guide device could achieve 90°steering angle of the wheel. The lateral displacement of wheel and the variation volume of camber angle when the wheel jumped up and down were chosen as the key evaluation factors in the design of suspension guide device. The proposed suspension guide device was established in ADAMS simulation software, and several different sizes of guide devices were chosen to carry out the simulation test. Therefore, the samples of lateral displacement volume and variation volume of camber angle were obtained. The optimal values of two arms in the independent suspension guide device with double lateral arms in unequal length were obtained by the data relevance and the linear regression statistics analysis. vehicle engineering; four wheel steering; double lateral arms suspension; ADAMS; regression analysis 10.3969/j.issn.1674-0696.2017.05.19 2015-12-02; 2016-03-11 深圳市科创委研究项目(JCYJ20140718171525577;ZDSYS20160229100057381;JCYJ20160525110808894;JCYJ20160525110851132) 李占玉(1983—),男,广东河源人,讲师,硕士,主要从事电动汽车结构方面的研究。E-mail:autolzy@szpt.edu.cn。 U463.41 A 1674-0696(2017)05-110-052 不等长双横臂悬架仿真分析

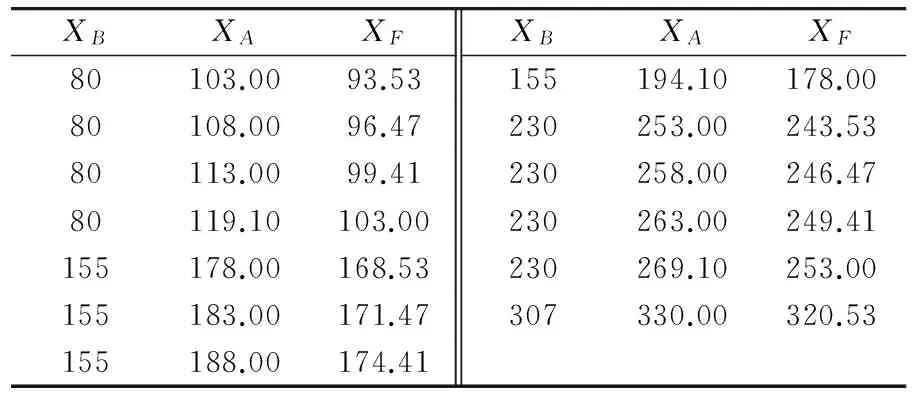



3 建模分析
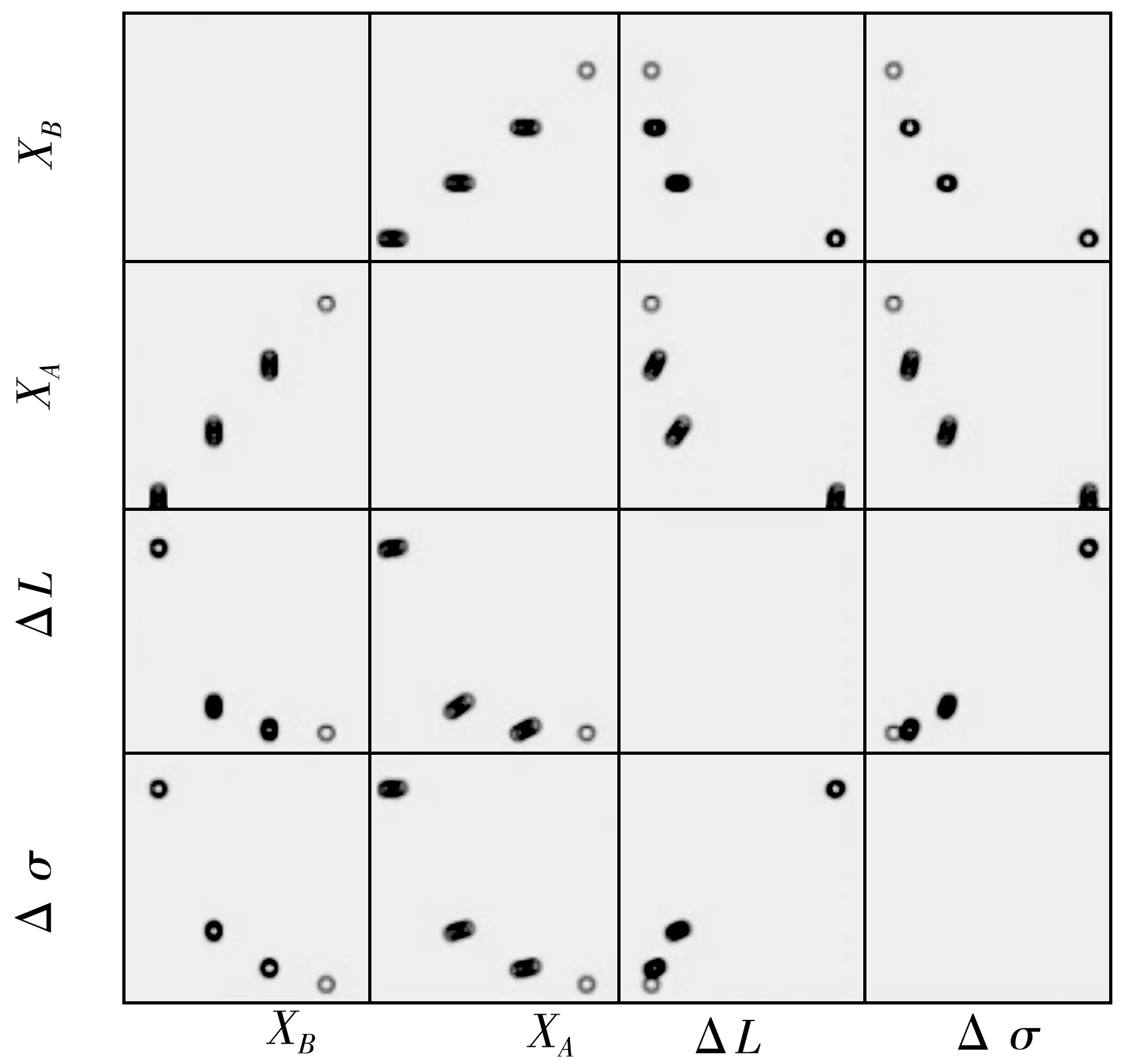
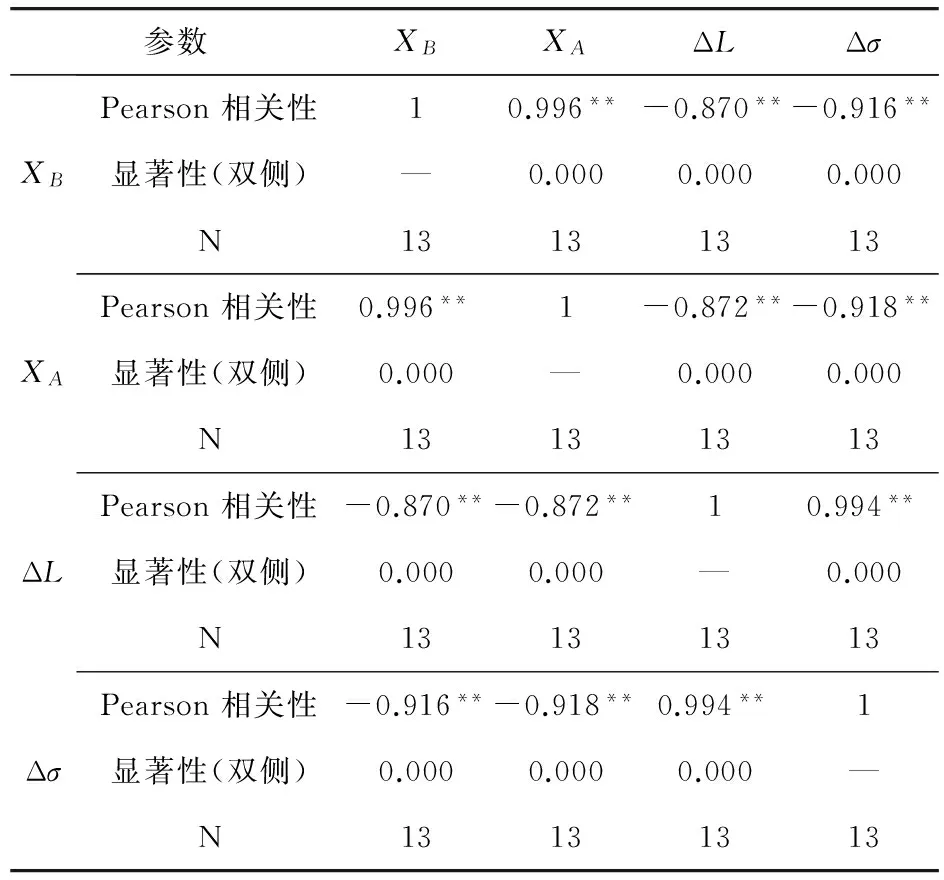
4 结 论
