中心孔对大功率核电汽轮机转子强度和稳定性的影响
2017-05-19冀润景
冀润景
(中国电能成套设备有限公司,北京 100080)
中心孔对大功率核电汽轮机转子强度和稳定性的影响
冀润景
(中国电能成套设备有限公司,北京 100080)
对大型整锻转子锻件开中心孔的原因和可能带来的问题进行了分析。研究分割叶轮和二次计算方法,推导了适用于整锻转子应力计算的矩阵方程,介绍开中心孔对转子强度、应力腐蚀的影响。同时,还讨论了轴系临界转速、不平衡响应以及扭振计算方法。最后基于计算结果分析了开中心孔对轴系稳定性的影响。
中心孔;二次计算;强度;轴系稳定性
对大功率核电汽轮机来说,以AP1000为例,低压转子(不带叶片)轴身直径2 785 mm、长11 180 mm,若采用红套转子则存在轮盘套装键槽等部位的应力腐蚀和飞射物概率增加的风险。若采用焊接转子方案,除焊接工艺的过程控制有较高要求,还需解决异种钢焊接时的碳扩散以及为提高可焊性而降低合金元素含量带来的FATT偏高问题[1]。因此,整锻转子仍是大功率核电汽轮机低压转子的一个主要发展方向。
对于百万千瓦级核电低压转子,钢锭质量达到600吨级,对钢锭的偏析控制、心部压实、晶粒度控制等工艺的提高需要一个成熟的过程。对于最初制造的几根转子,从汽轮机厂家以及技术引进方角度,都希望通过打中心孔来消除锻件中心部位的薄弱部分,并可对中心部分的质量进行评估。
对转子开中心孔带来的问题主要体现在:①对转子应力分布的影响,文献[2]和[3]分别用有限元法和解析公式对中心孔带来的转子应力变化进行了分析;②运行中中心孔处进油进水带来的转子涡动,文献[4]和[5]分别介绍了中心孔进油、进水引起的振动故障的诊断和解决方法。
本文从工程实用方法出发,通过计算结果的比对,分析大功率核电汽轮机低压转子开中心孔后对轮盘强度和轴系稳定性的影响。
1 中心孔对叶轮强度的影响
1.1 叶轮应力计算方法
对叶轮的微元体,以位移为未知量,由弹性力学可得叶轮应力基本计算公式[6]:
A=ρw2(1-μ2)/E
(1)
式中R——叶轮某截面的半径;v,y——半径R处径向位移和叶轮厚度;μ,ρ,E——材料泊松比、密度和弹性模量;ω——叶轮角速度。
求得位移后,根据虎克定律以及应变几何方程,按式(2)写成矩阵方程求得各点的应力值。
(2)
式中σr、σθ——径向、切向应力。
除等厚度叶轮外,按这些方法直接求解微分方程比较困难,在工程实际中常用近似方法计算。以式(1)为基础,结合等厚度叶轮的计算方法,建立矩阵方程,使得方程更为简明,计算过程更为方便。
将转子沿轴向分割为多个单独的叶轮,再将叶轮沿径向近似分为若干等厚度段,分段数越多计算越精确,工程上认为一般9~10段可满足需要,每段的厚度改变量不宜大于10%~20%。相邻两段的应力示意图见图1。

图1 相邻两段的应力示意图
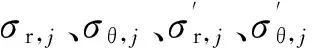
(3)
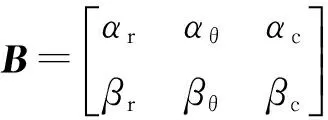
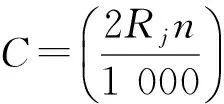
相邻两段间的应力传递也可写成矩阵方式
(4)
式中yj——第j段的厚度。
至此,给定叶轮边界应力值,即可按式(3)和式(4)直接计算出叶轮各部位的应力值。
在进行叶轮计算时,需要确定边界条件,叶轮外表面的径向应力σr,a是有叶片离心力及叶根与轮缘连接部分的离心力引起,可按式(5)计算:
σr,a=(ZFB+λFrim)/2πRaya
(5)
式中Ra,ya——叶轮外径、外缘厚度;FB,Frim——叶片、半径Ra以上轮缘部分的离心力;Z——叶片数量;λ——系数。
对空心转子的内表面,径向应力σr,i=0,对实心转子,则中心零半径上的径向、切向应力相等,σr,i=σθ,i。
1.2 基于应力叠加原理的简化计算
叶轮任意半径上的应力是由σr,a、σr,i以及叶轮质量离心力3部分组成。根据应力叠加原理,这3部分载荷互相独立[7],因此可采用二次计算法,使计算过程更为简化。
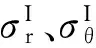
(6)
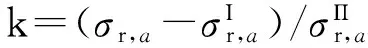
对于实心叶轮,两次计算分别给定σr,i=σθ,i,可以为任意值,n分别为工作转速和0。
1.3 中心孔对转子叶轮强度的影响计算分析
以某百万千瓦级核电汽轮机低压转子为例,该转子为整锻转子,末级叶片长1 375 mm,最大半径5 550 mm,其余尺寸、结构见图2。
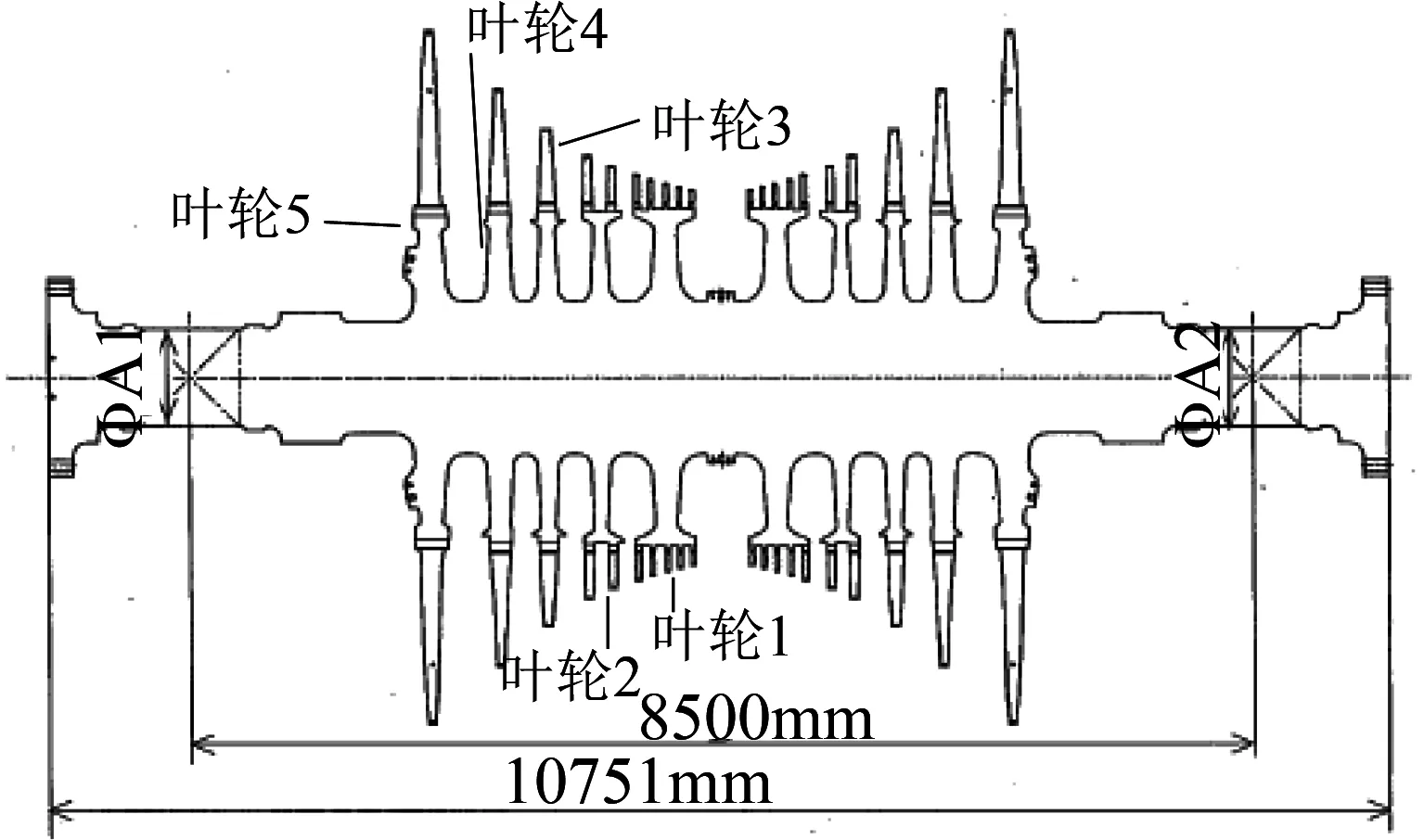
图2 大功率核电汽轮机转子结构示意图
分别按开中心孔(直径305 mm)和实心转子进行稳态工况下的强度校核,同时考虑到核电汽轮机的蒸汽参数以及转子直径,特别对应力腐蚀进行校验,见图3、图4、图5。从计算结果看,相同条件下,实心转子开中心孔后,局部最大应力水平和整体应力水平大大提高,但均满足强度要求。
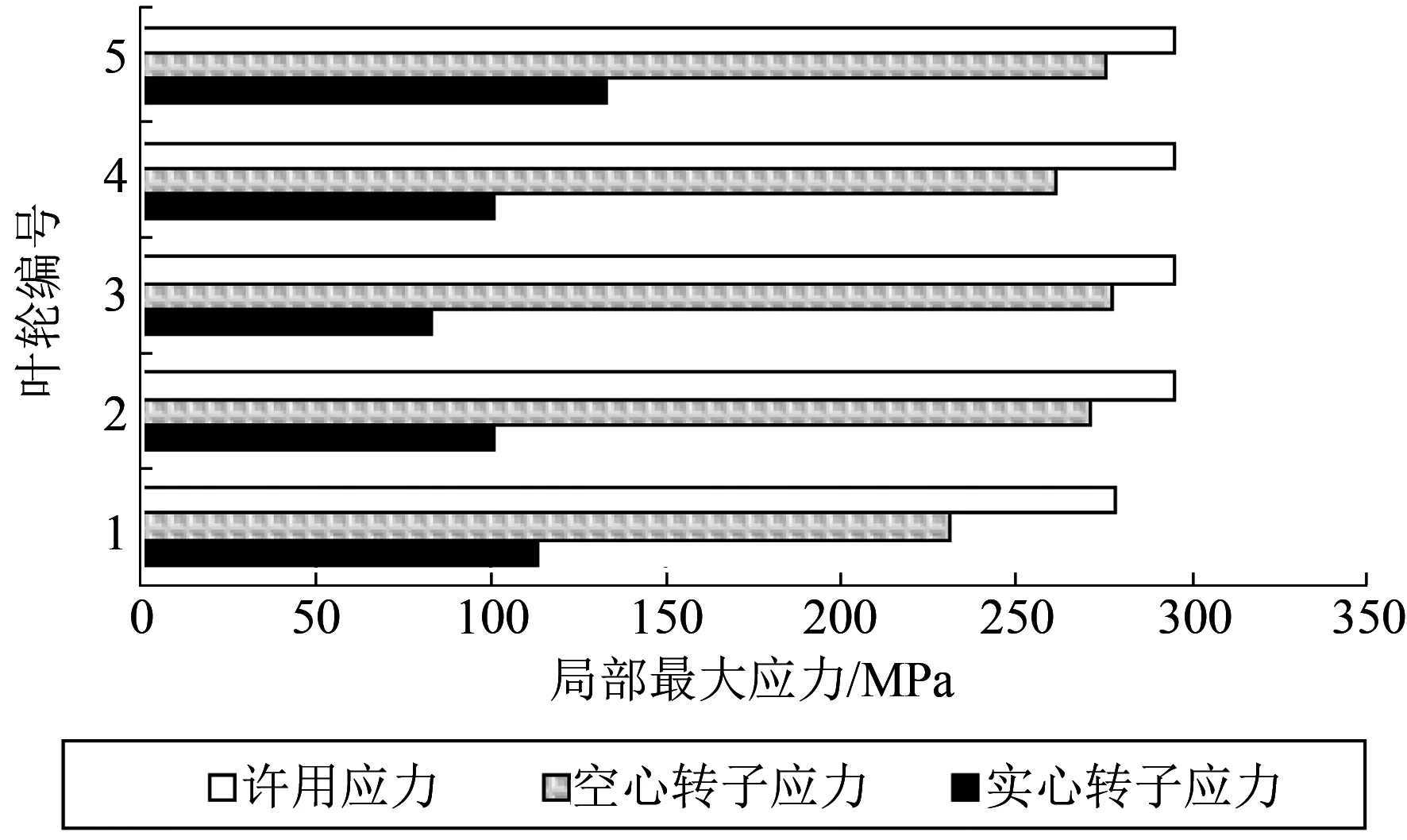
图3 局部最大应力计算结果
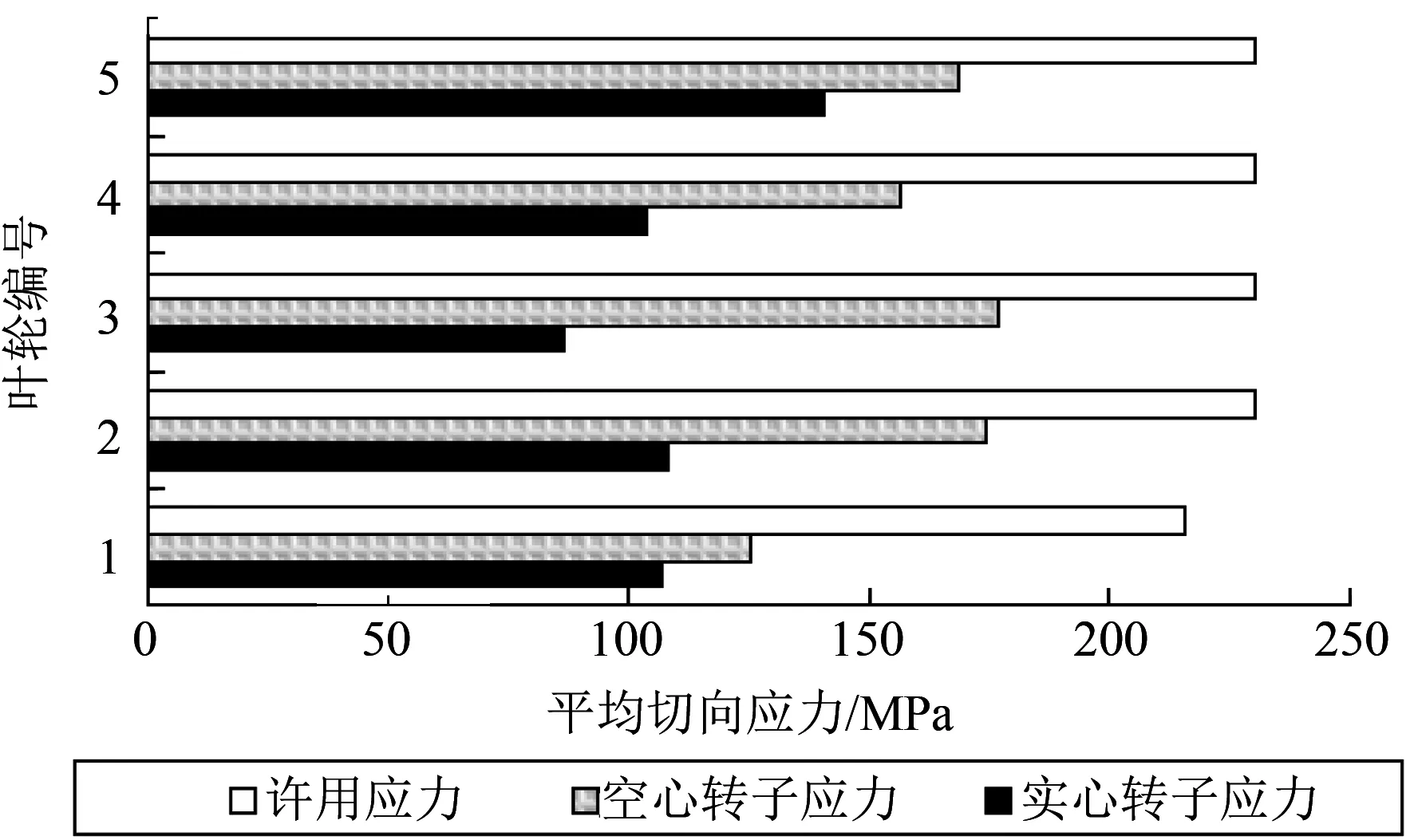
图4 平均切向应力计算结果
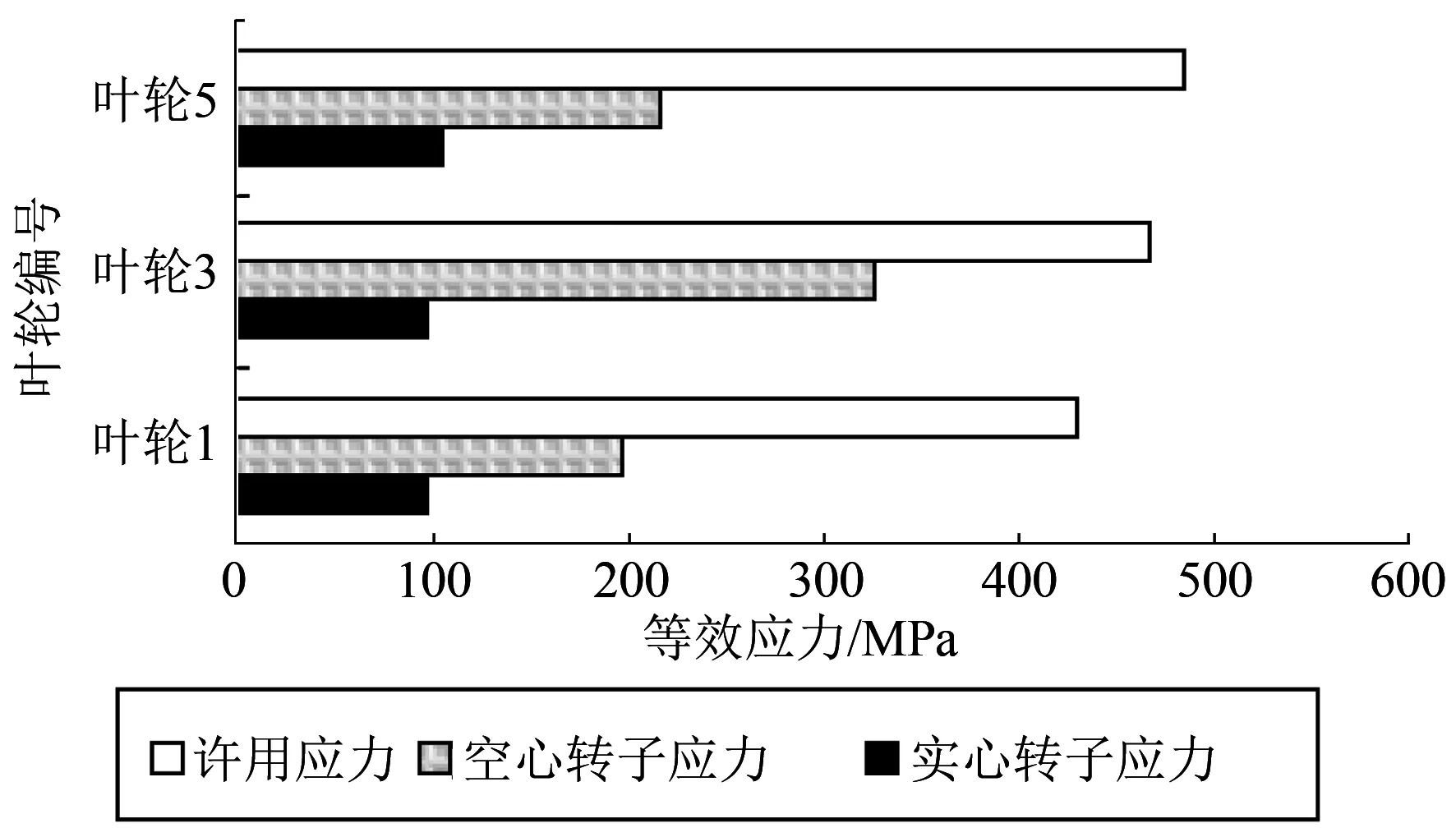
图5 典型部位应力腐蚀校验情况
空心叶轮的径向应力从外表面开始,随叶轮半径减小不断增大,到达最大值后开始减小,直到内孔处减小至0,而切向应力则随半径减小不断增大,到内孔处达到最大。而实心叶轮的径向、切向应力随半径减小增大,到中心处两者达到最大值并相等。因此说,空心转子的应力水平高的主要由切向应力贡献,这与很多文献记载的规律相同[8-10]。
2 中心孔对汽轮机轴系稳定性的影响
轴系稳定性计算包括临界转速、不平衡响应、扭振等内容。以下对低压转子开中心孔后,轴系稳定性的计算进行分析。
2.1 中心孔对轴系临界转速的影响
无质心偏移的变截面转子自由振动的阵型方程:
(7)
式中I、F——横截面惯性矩;E——横截面面积;Y(x)——挠度。
直接求解式(7)是不可能的,工程上采取试凑方法,主要有初参数法和传递矩阵法。传递矩阵法实质上就是初参数法的矩阵算法,具有程序简单、数值稳定性高并且维数不随自由度增大而增大[8],在工程上广泛应用。
传递矩阵法的原理是将轴系离散为圆盘、轴段、支撑等若干部件,建立部件两端截面状态向量间传递关系,利用连续条件求得任意截面与初始截面间的关系,并通过边界条件进行涡动频率搜索得到临界转速。对任一截面i构建状态向量Zi=[yiθiMiQi]T,其中yi、θi、Mi、Qi分别是截面i处的挠度、斜率、弯矩和切力。
对带有弹性支撑的刚性薄圆盘,有:
(8)
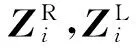
对无质量的等截面弹性轴段,有:
Zi+1=HiZi
(9)
式中Hi——轴段的传递矩阵;l——轴段长度;v——材料剪切变形系数;Zi+1,Zi——轴段右、左截面状态向量。
结合式(8)—式(9)可以看出,任意截面i的状态向量都可以表示为初始截面状态向量各元素的线性组合,考虑到初始截面一般是自由端,切力和弯矩为0,则任意截面i状态向量Zi:
(10)
式中Wi-1——系数矩阵,由传递矩阵的乘积求出。
显然对末端面N,可得出:
(11)
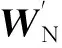
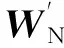
以百万千瓦级核电汽轮机组为例,其轴系由1根高压转子、3根低压转子和1根发电机转子组成,每根转子由2个轴承支撑。低压转子开孔前后的轴系弹性临界转速计算对比如表1所示。

表1 临界转速计算值 r/min
从表1计算结果看,开孔前后临界转速计算值除低压2号转子略有差异外,其余完全相同,并且均满足10%的额定转速避开率,这说明开中心孔对轴系临界转速几乎没有影响。分析其原因,在进行传递矩阵计算时,开孔对计算结果的影响体现在Jp、Jd、I的计算上,由于开孔直径305 mm与转子直径相比很小,在计算时均为内外径比值的4次方,对结果的影响则更小。
2.2 中心孔对不平衡响应的影响
不平衡响应的计算是通过按规定对各轴段施加不平衡量,采用传递矩阵计算求得转子振动的幅频响应,得到转子的各阶阻尼临界转速。其频幅曲线的峰值越高,带宽越窄,则不平衡响应越敏感,稳定性越差(见表2)。各汽轮机厂对轴系不平衡响应的评价不完全相同,我国习惯用对数衰减率δ做判据,而日本习惯采用Q因子准则[9]。

表2 不平衡响应计算结果
对于不平衡响应的判定,目前尚无统一标准。一般来说最小对数衰减率应至少大于0,其中国内有厂家要求大于0.2,西门子则要求大于0.1。从表2的计算结果看,均能满足。另外,开孔前后对数衰减率的计算值几乎没有差别,说明开中心孔对转子的不平衡响应影响甚小。开孔后各转子Q因子分布如图6所示。
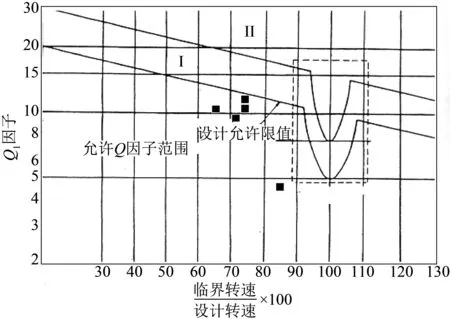
图6 开孔后各转子Q因子分布
对Q因子的判定,如果在图6中曲线Ⅰ以下,认为稳定性是好的;在曲线Ⅰ和Ⅱ之间,也可认为稳定性是良好的;在Ⅱ以上,则认为稳定性较差。表2的计算结果说明开中心孔对Q因子的计算影响甚小,与对数衰减率的情况相同。事实上,不难发现,对数衰减率与Q因子成反比,乘积为π,因此两者的计算受开孔的影响情况相同。从图6看,开孔后各转子的Q因子均分布在曲线Ⅰ以下,说明开孔后稳定性是好的。
2.3 中心孔对扭振及剪切应力计算的影响
对运行中的轴系,当发生超速或发电机两相短路时,会发生扭振频率与工频或倍频耦合,以及短路应力问题。扭振计算同样采用传递矩阵法,一般仅进行二相短路工况计算,扭振频率的计算受轴系长度、惯性直径、附加转动惯量以及轴系扭转阻尼特性等影响。通过计算可得出,开中心孔对扭振频率的影响不大[10],原因与横振临界转速的情况一样,开孔后轴系各阶扭振频率满足以下避开要求:45 Hz

表3 二相短路剪切应力计算结果
由表3可以看出,开孔对二相短路应力的计算影响不大,开孔前后二相短路应力计算值均满足许用要求。
3 结语
(1)针对整锻转子应力计算,对分割叶轮计算方法和基于应力叠加原理的二次计算方法进行了深入探讨,推导出矩阵计算公式,不仅方便计算,而且工程实用性强。
(2)对某大功率核电汽轮机低压转子开中心孔前后的转子应力计算结果表明,开孔后应力水平大幅提高,但通过强度校核和应力腐蚀校核,仍在允许范围。造成开孔后应力高的原因在于空心叶轮内表面径向应力为0,切向应力达到最大。
(3)对轴系临界转速、不平衡响应和稳定性、扭振及剪切应力计算方法进行了深入探讨。计算结果表明开中心孔对轴系振动特性影响很小,工程上可以不考虑。原因在于中心孔直径与转子直径相比很小,对计算影响不大。
(4)对于大型整锻转子锻件,当受到热加工工艺制约必须开中心孔时,应确保其强度通过校核。
[1] 冀润景. 核电汽轮机选型中需关注的几个问题分析[J]. 发电设备, 2015, 29(3): 220-224.
JI Runjing. Problems concerning type selection of nuclear steam turbines[J]. Power Equipment, 2015, 29(3): 220-224.
[2]吴锋,盛德仁,蒋志强,等. 汽轮机转子中心孔对转子温度和应力分布的影响[J]. 机电工程, 2006,23(11): 1-3.
WU Feng, SHENG Deren, JIANG Zhiqiang, et al. The influence made by the central hole of steam turbine rotor to temperature and stress distribution of rotor[J].Mechanical & Electrical Engineering Magazine,2006,23(11):1-3,7.
[3]冀润景. 汽轮机中心孔转子与实心转子的性能对比[J]. 热力发电, 2015, 44(1): 115-118.
JI Run-jing. Performance comparison between hollow rotor and solid rotor in steam turbines[J]. Thermal Power Generation,2015,44(1):115-118.
[4]张其显,刘晓锋. 汽轮机转子中心孔进油诱发异常振动故障分析诊断[J]. 汽轮机技术, 2007, 49(1): 57-59.
ZHANG Qixian, LIU Xiaofeng. The analysis and diagnosis of abnormal vibration induced by oil-trapped inside the central hollow steam turbine′s rotor[J]. Turbine Technology,2007,49(1):57-59.
[5]张云忠,彭龙,杨春意. 汽轮机转子中心孔进水引起的机组振动故障[J]. 云南电力技术, 2009, 37(4): 60-61.
ZHANG Yunzhong, PENG Long, YANG Chunyi. Power unit vibration fault caused by water fed into center hole of steam turbine rotor[J]. Yunnan Electric Power,2009,37(4):60-61.
[6]李铜桥,张玉龙. 汽轮机叶轮强度计算方法[J]. 汽轮机技术, 2008, 50(1): 20-22.
LI Tongqiao, ZHANG Yulong. Strength calculation method for blade wheel of steam turbine[J].Turbine Technology,2008,50(1):20-22.
[7]吴厚钰. 透平零件结构和强度计算[M]. 北京:机械工业出版社, 1982.
[8]中国动力工程学会. 火力发电设备技术手册-第二卷-汽轮机[M]. 北京:机械工业出版社, 1999.
[9]王骏,高远. 超临界及超超临界汽轮机蒸汽激振和轴系稳定性分析[J]. 能源研究与利用, 2009(6): 18-23.
WANG Jun, GAO Yuan. Analysis of steam-excitel vibration and shafting stability of supercritical or ultra-supercritical stem turbine unit[J]. Energy Research and Utilization,2009(6):18-23.
[10]刘辉,关璐奇. 核电AP1000低压转子有无中心孔分析优化[J]. 机械工程师, 2014(3): 32-33.
(本文编辑:赵艳粉)
Influence of Central bore on Rotor Strength and Stability for Large Capacity Nuclear Turbine
JI Runjing
(China Power Complete Equipment Co., Ltd., Beijing 100080, China)
This paper analyzes the purposes and possible problems for opening the central bore in large integral rotor forging. It also discusses the method of dividing impeller and two times calculation, derives the matrix equation suitable for integral rotor stress calculation, and analyzes the influence of center bore on rotor strength and stress corrosion. The calculation method of critic speed, unbalance response and torsional vibration of rotor assembly is discussed, and influence of center bore on the stability of rotor assembly is analyzed based on the calculation result.
central bore;two times calculation;strength;stability of rotor assembly
10.11973/dlyny201702023
冀润景(1981—),男,硕士,高级工程师,从事核电汽轮机设备监进技术及管理工作。
TK267
A
2095-1256(2017)02-0196-05
2016-11-28
