基于频谱分析的储能容量配置方法

潘 杰，李久广

(1. 上海交通大学，上海 200240；2. 上海太阳能科技有限公司，上海 201108)

基于频谱分析的储能容量配置方法

潘 杰1，李久广2

(1. 上海交通大学，上海 200240；2. 上海太阳能科技有限公司，上海 201108)

太阳能等新能源发电存在随机性和波动性，为了平抑功率变化对配电网的危害，提出了基于频谱分析的储能设备容化配置方法。新能源输出功率通过采用快速离散傅里叶变换的方式进行频谱分析。基于频谱分析结果，结合储能设备充放电效率、储能设备的充放电水平和新能源系统功率输出波动率的范围等约束条件，确定储能设备最小容量。仿真分析数据来源于上海太阳能科技有限公司。

储能容量；频谱分析；快速离散傅里叶变换；平抑功率波动

光伏输出功率取决于光照强度的变化，具有随机性和波动性。当配电网接入的光伏发电容量超过电网规定的接入比例，光伏功率波动将增加电网的调整负担，增加储能设备是目前较为理想的解决途径，可以平滑光伏功率波动，改善接入电网的光伏电能质量。但是目前储能设备的成本是必须要考虑的因素，因此研究如何优化确定储能设备的容量具有重要意义。文献[1]提出了基于饱和控制理论优化储能设备容量的方法，建立了以最小化储能容量为优化目标，以总体收敛速度和稳定域为约束条件的优化模型，但这个理论忽视储能设备与间歇式新能源配合的问题。文献[2]提出了基于低通滤波器原理优化储能设备容量的方法，但是该方法没有考虑储能设备的损耗，以及充放电水平，与实际有出入。

本文利用快速离散傅里叶变换(FFT)对新能源输出功率进行频谱分析[3-4]，基于FFT的频谱分析结果，结合储能设备充放电效率、储能设备的充放电水平和分布式能源发电系统功率输出波动率的范围等约束条件，确定储能设备最小容量。

1 典型样本数据分析

为了平抑新能源发电的功率输出波动，需要收集新能源发电功率输出的典型样本数据。样本数据的来源主要是记录新能源发电运行的实际历史数据，包括采样周期、样本数据的片段长度等样本数据参数，都与研究密切相关。

(1)样本的采样周期。储能设备用于平抑新能源短期功率波动时，样本采集尺度常是秒级到数十分钟级[5]。由于1～100 s时间尺度内的功率波动对配电网的影响尤为明显[6-7]，一般采用抑制0.01～1.00 Hz频段范围内的输出功率波动。储能设备用于平抑新能源长时间功率波动时，其平抑的时间尺度一般是数十分钟级到小时级。对于储能设备在平抑功率波动情况下的容量配置，本文选用样本采样周期是1 min。

(2)样本数据的片段长度。短时平滑输出模式的数据片段长度一般选为1 h，而长时平滑模式的数据片段长度一般选为1天。由于太阳能等新能源发电具有较强的季节性，数据片段需要选取各个季节典型日的样本数据。在实际操作中，可酌情考虑延长数据片段长度，比如延长到1周，便于应对辐照强度变化波动随机性较大的问题。同时，数据片段长度也可保持1天。

2 储能设备功率确定

为了达到平抑新能源功率输出波动的效果，并且保持储能设备连续稳定运行，首先必须确定储能设备功率输出和最大充放电功率。根据给定的新能源功率输出历史样本数据，对数据进行频谱分析。通过频谱分析的结果，可确定所需补偿的最小频率范围和对应的目标功率输出。满足目标功率输出波动率约束条件的储能设备最大充放电功率可以通过模型仿真获得。具体步骤如下：

(1)光伏系统的功率输出样本数据是Pg=[Pg(1)，…,Pg(n)，…,Pg(Ns)](Pg(n)是第n个光伏功率值，kW；Ns是功率样本的个数)。对功率输出样本数据Pg进行快速离散傅里叶变换，获得幅频结果Fg和fg:

(1)

式中Fg——功率值列向量；fg——频率列向量；Fg(n)=Rg(n)+jIg(n)——快速傅里叶变换后的第n个频率对应的幅值；Rg(n)，Ig(n)——幅值Fg(n)的实部和虚部。

(2)

式中fs，Ts——光伏发电输出功率样本的采样频率和采样周期。

由奈奎斯特采样定理知，样本数据的最高频率fN≤fs/2。由于快速傅里叶变换数据具有对称性，因此，Fg以频率fs/2为对称，两侧对称数据互为共轭，模值相等。在进行分析时，只需考虑对称轴的一侧的幅频特性就可以了。

经过快速傅里叶变换后的幅值Fg并不是实际的信号幅值，实际幅值Dg表示如下：

(3)

在分析中，实际信号幅值Dg与对应的频率fNG可表示为

(4)

(2)通过频谱分析结果，计算确定满足功率输出波动约束的目标功率输出和对应的储能设备补偿频段。

参照频谱分析结果，假设fps是Dg对应的补偿频段，fps′是以奈奎斯特频率fs/2为对称的频段。F0=[F0(1),…,F0(n),…,F0(Ns)]T以来表示经过储能设备补偿后的频谱信号数据。其中，将补偿频段过滤掉，相当于储能设备对该频段进行了补偿，消除了该频段的功率波动，其他频段数据信号不变，即：

(5)

对F0进行快速傅里叶逆变换，得到的结果就是目标输出功率P0，则有

P0=[P0(1),…,P0(n),…P0(Ns)]T

(6)

式中P0(n)——第n个数据采样点的目标输出功率，kW。

储能设备其补偿效果的评价标准是功率输出波动率。在Tc时间段内假设功率波动率用ηTc表示：

(7)

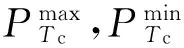
只有符合功率波动率不超过设定的上限值，目标功率才算达到要求：

(8)

如何获得最小的补偿容量并同时满足输出波动率的要求，就是储能设备容量优化的目的。采用试差法依次来确定系统补偿频段，从高频开始，慢慢减小频段值，依据该方法分析补偿后的波动率是否达到目标要求，从而得到在达到波动率目标的条件下储能设备容量最小的补偿频段。

(3)确定出储能设备所需要的最大充放电功率。根据目标输出功率P0和原始输出功率Pg，可得储能设备的功率Pb0：

Pb0(n)=P0(n)-Pg(n)

(9)

Pb0(n)有正有负，当Pb0(n)为正值时表示储能设备放电；当为负值时表示储能设备充电。在实际运行中存在能量的损耗，储能设备完成一次完整充放电循环的效率称为储能设备的综合利用效率，用ηES表示。则储能设备的实际充放电功率Pb=[Pb(1),…,Pb(n),…,Pb(Ns)]T为：

(10)

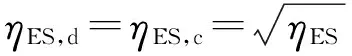
综合所述，在整个样本数据时间内，Pb的绝对值的最大值就是满足目标输出功率的储能设备的最大充放电功率，即：

PES0=max{|Pb(n)|}

(11)

3 储能设备容量确定

储能设备容量分析计算步骤如下。

(1)由于Pb已经确定，累计计算各采样点的储能设备充放电的电量，得到相对于初始状态的不同采样时刻储能设备的能量波动，即

(12)

式中Eb,acu(m)——储能设备m个点的采样时刻相对于初始时刻的电量变化值，也可以认为是前m个采样周期内储能设备累计充放电的和。

(2)根据储能设备在整个样本数据周期内的能量波动，计算储能设备最大和最小能量之差，同时结合能量剩余水平的约束，得到储能设备的最优容量，也就是储能设备的额定容量值是：

(13)

式中 max{Eh,acu(m)}——整个分析样本数据中，储能设备相对初始状态下能量变化的最大值； min{Eb,acu(m)}——整个分析样本数据中，储能设备相对初始状态下能量变化的最小值；Cup，Clow——储能设备运行中的能量剩余水平的上下限约束，在理想状态下，Cup=1，Clow=0，考虑到实际情况，避免过充和过放对储能设备的损害，影响使用寿命，一般Cup、Clow在[0,1]内取值。

4 算例仿真与分析

为了验证储能设备用于平抑以光伏发电为代表的新能源发电系统输出功率的容量确定方法，采用的光伏发电功率数据的时间为2015年4月21日7：00-15：20。当天天气为阴天，地点在上海太阳能科技有限公司微网示范电站的记录数据，每分钟一个数据，共取500个功率值，光伏发电系统额定功率是130 kW。光伏发电功率输出波形图如图1所示。由于光伏最大输出功率是52.596 kW，平均输出功率是15.359 kW，最小输出功率是5.518 kW，10 min最大功率波动值是是25.470%。储能设备的综合充放电效率是88.00%，假定充电和放电效率相等，则均为93.81%；假设储能设备能量剩余水平的上限取 1.0，下限取0.3。光伏发电功率输出波动控制目标，10 min最大功率波动设为10%。

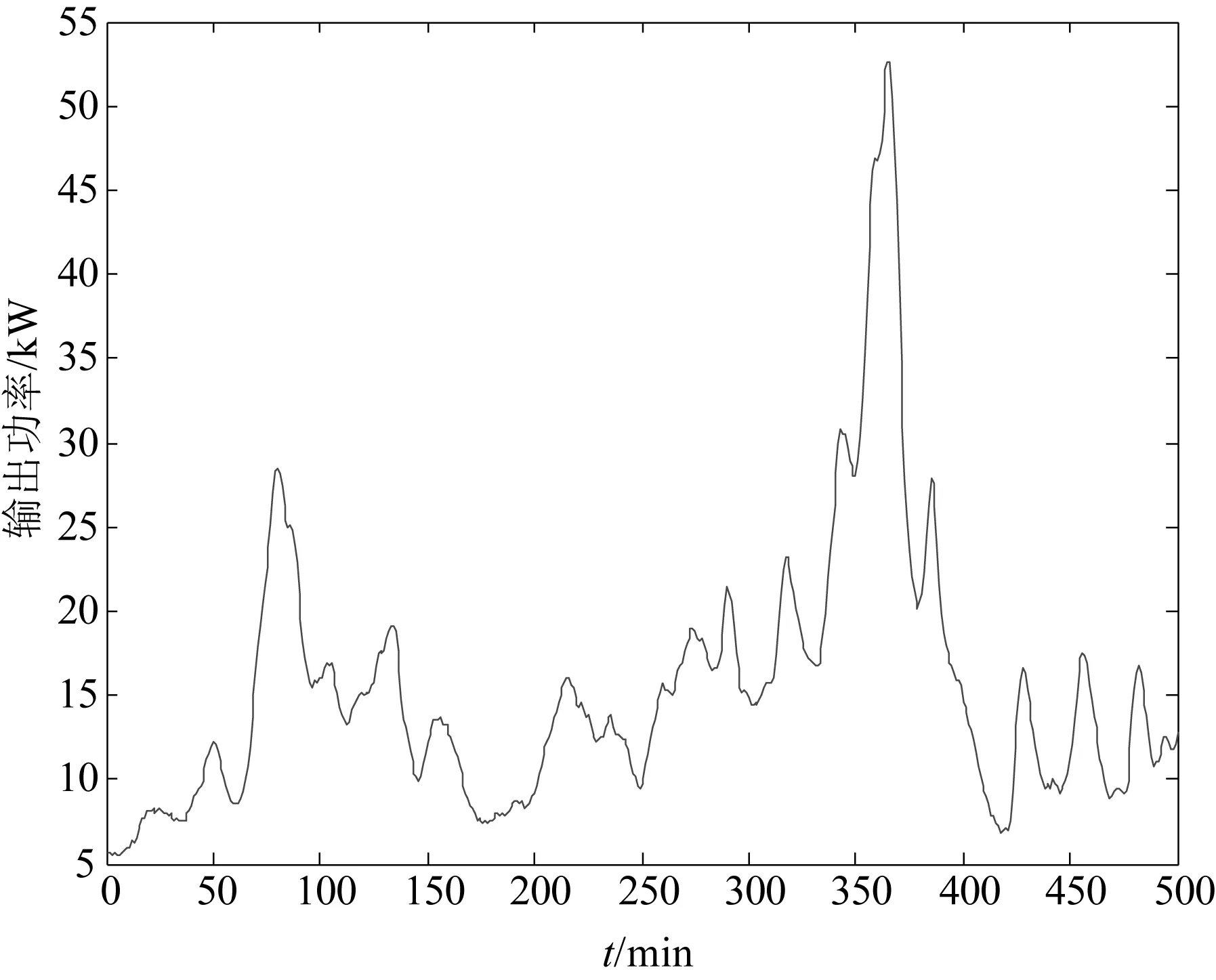
图1 光伏发电功率输出波形图

首先，通过快速离散傅里叶变换对光伏发电输出的功率样本数据进行频谱分析，得到的频谱图如图2所示。图2给出了样本数据在奈奎斯特频率fN=8.333×10-3Hz之前的幅频特性。

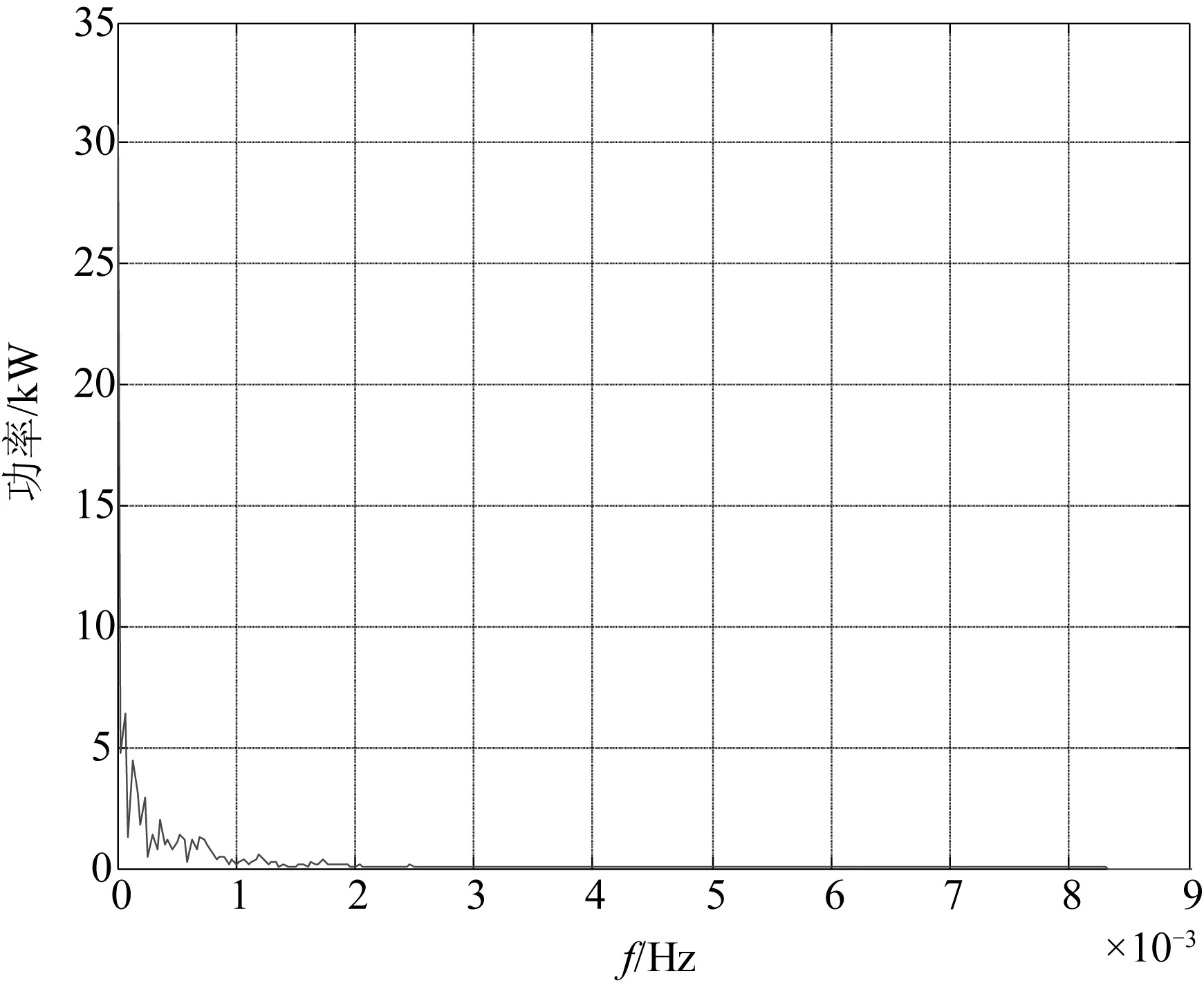
图2 光伏发电功率频谱分析结果

从图2可知，从频谱分析结果可以确定满足功率波动约束条件的储能设备最小补偿频段范围和对应的理想目标输出。为了方便描述，用频段范围对应的周期值来说明。假设补偿周期范围是[Tl，Tu](Tl、Tu分别是补偿周期的下限和上限)。根据推导的储能设备功率和容量确定方法，从高频波动分量开始补偿。所以补偿周期下限Tl是2 min(奈奎斯特频率对应的周期)，用试差法查找满足目标功率输出的储能设备补偿周期上限，当Tu=40 min时，最大波动率是10.68%，继续增大周期；当Tu=50 min时，最大功率波动率是9.89%，则对应的最小补偿范围是Tu=50 min。对应的目标功率输出波形图如3所示。

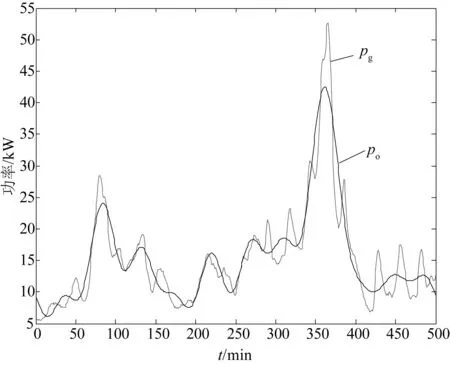
图3 补偿周期范围[2 min, 50 min]时，Pg和P0的功率输出

由目标输出功率P0，则可求得所需储能设备补偿功率Pb0。其功率输出如图4所示。

图4 补偿周期范围[2 min, 50 min]时，储能设备Pb0的功率输出

由于设定储能设备的综合充放电效率是88%，并且充电效率预防点效率相等，均为93.81%，Pb0值最大值是Pb0(376)=10.302 1 kW，储能设备是放电状态，除以放电效率后得PES0是10.98 kW；Pb0值最小值是Pb0(366)=-11.319 5 kW，储能设备是充电状态，乘以充电效率算得PES0是10.62 kW，则所需储能设备最大充放电功率值是10.98 kW。

由Pb0再经充放电效率校正后得到Pb，然后根据式(12)可得到储能设备相对初始状态充放电能量变化，如图5所示。

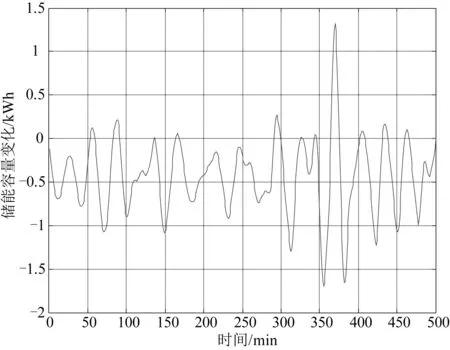
图5 能量变化图

由Eb,acu能量变化图，结合能量剩余水平上限取1.0，下限取0.3，可求得储能设备额定容量值：

4.305 kWh

选取的数据样本功率最大值是52.596kW，对于120kW的光伏电站储能容量配置可用类比的方法进行。经校正后，平滑光伏发电功率输出波动在10%以内，所需储能设备最优容量配置方案如表1所示。

表1 最优储能容量配置方案

5 结语

基于频谱分析的方法，首先对采样数据进行快速傅里叶变换，然后根据频谱图选择要平抑的频段，结合平抑目标，采用试差法，最终达到平抑效果。在此基础上可以确定储能设备充放电的最大功率值以及所需容量值。由于本方法考虑了充放电效率以及储能设备能量剩余水平上下限的约束，求得的结果更符合实际。

[1]

吴云亮，孙元章，徐箭，等．基于饱和控制理论的储能设备容量配置方法[J]．中国电机工程学报，2011 ，31(22)：32-39．

WUYunliang,SUNYuanzhang,XUJian,etal.Determinationmethodologyforenergystoragecapacitybasedonsaturationcontroltheory[J].ProceedingsoftheCSEE,2011,31(22)：32-39．

[2]靳文涛，马会萌，谢志佳，等．电池储能设备平滑风电功率控制策略[J]．电力建设，2012，33(7) ：7-11．

JINWentao,MAHuimeng,XIEZhijia.Windpowersmoothingcontrolstrategyofbatteryenergystoragesystem[J].ElectricPowerConstruction,2012,33(7):7-11.

[3]王成山，于波，肖竣，等．平滑可再生能源发电系统输出波动的储能设备容量优化方法[J]．中国电机工程学报，2012 ，32(16)：1-8．

WANGChengshan,YUBo,XIAOJun,etal.Sizingofenergystoragesystemsforoutputsmoothingofrenewableenergysystems[J].ProceedingsoftheCSEE,2012,32(16):1-8.

[4]徐岩，张晓明，王瑜，等．基于离散傅里叶变换的频谱分析新方法[J]．电力系统保护与控制，2011，39(11)：38-43.

XUYan,ZHANGXiaoming,WANGYu,etal.AnewmethodofspectrumanalysisbasedonDFT[J].PowerSystemProtectionandControl,2011,39(11)：38-43.

[5]YOSHIMOTOK,NANAHARAT,KOSHIMIZUG.Analysisofdataobtainedindemonstrationtestaboutbatteryenergystoragesystemtomitigateoutputfluctuationofwindfarm[C]//ProceedingofCIGRE/IEEEPESJointSymposiumonIntegrationofWide-ScaleRenewableResourcesIntothePowerDeliverySystem,Paris,France:2009:1-5.

[6]BREKKENTKA,YOKOCHIA,VONJOUANNEA,etal.Optimalenergystoragesizingandcontrolforwindpowerapplications[J].IEEETrans.onSustainableEnergy, 2011, 2(1):69-77.

[7]JIAHX,FUY,ZHANGY,etal.Designofhybridenergystoragecontrolsystemforwindfarmsbasedonflowbatteryandelectricdouble-layercapacitor[C]//ProceedingofIEEEPESAsia-PacificPowerandEnergyEngineeringConference,Chengdu,China,2010:1-6.

(本文编辑：赵艳粉)

Energy Storage Capacity Configuration Based on Spectrum Analysis

PAN Jie1, LI Jiuguang2

(1. Shanghai Jiao Tong University, Shanghai 200240, China;2. Shanghai Solar Energy Technology Co., Ltd., Shanghai 201108, China)

There exist randomness and volatility in the generation of new energy such as solar power. In order to prevent the harm of power change on power distribution network, this paper proposes energy storage equipment capacity configuration method based on the spectrum analysis. The spectrum analysis is made on new energy power output by using fast discrete Fourier transform. Then combined with the spectrum analysis result, and the constraints in the energy storage device charge-discharge efficiency and level, and the new energy system power output volatility range, it determines the minimum energy storage equipment capacity. The simulation analysis data is obtained from Shanghai Solar Energy Technology Co., Ltd.

energy storage capacity; spectrum analysis; fast discrete Fourier transform; smooth power fluctuation

10.11973/dlyny201702011

潘 杰(1987—)，男，硕士研究生，从事微电网应用技术研究。

TM314

A

2095-1256(2017)02-0140-05

2016-12-25