角接触球轴承刚度研究

张振强，王东峰，周海波

（1.洛阳轴研科技股份有限公司，河南 洛阳 471039；2.河南省高性能轴承技术重点实验室，河南 洛阳 471039；3.滚动轴承产业技术创新战略联盟，河南 洛阳 471039）

角接触球轴承刚度研究

张振强1,2,3，王东峰1,2,3，周海波1,2,3

（1.洛阳轴研科技股份有限公司，河南 洛阳 471039；2.河南省高性能轴承技术重点实验室，河南 洛阳 471039；3.滚动轴承产业技术创新战略联盟，河南 洛阳 471039）

针对角接触球轴承的接触角、轴向力以及轴承刚度之间的关系问题，通过对轴承建立静力平衡方程，对具有不同接触角(其它参数相同)的轴承进行刚度研究。研究表明：在相同轴向力作用下，轴承自由接触角越大，其轴向刚度越大，但轴向位移、径向刚度以及刚度比值(径向刚度/轴向刚度)都越来越小；在相同接触角情况下，轴向力越大，其轴向位移、轴向刚度和径向刚度都越来越大，但其刚度比值会越来越小。

角接触球轴承；接触角；轴向力；刚度

1 前言

角接触球轴承的刚度计算是一个典型的非线性问题，其刚度值随轴承实际受力情况的不同而呈非线性变化的趋势；即使在相同受力情况下，轴承内部参数的不同也将引起刚度结果产生差异。虽然文献[1,2]等都对轴承刚度进行过研究，但研究对象均为某特定参数轴承，没有进行过不同轴承之间的对比，基于此，本文通过对轴承建立静力平衡方程，对具有不同接触角(其它参数相同)的轴承进行刚度研究，以期能够揭示轴承刚度的基本规律。

2 符号说明

A—— 沟道沟曲率中心之间的距离，

S—— 内、外滚道沟曲率中心轨迹之间的距离，

R—— 滚道沟曲率中心轨迹半径，

Q—— 球-滚道法向载荷，

δ—— 位移或接触变形，

δa—— 相对轴向位移，

δr—— 相对径向位移，

ri—— 内沟曲率半径，

ro—— 外沟曲率半径，

dm—— 轴承节圆直径，

Z—— 滚动体数量，

θ—— 相对角位移，

Dw—— 滚动体直径，

αo—— 自由接触角，

α—— 安装接触角，

φ—— 方位角，

Fa—— 轴向力，

Fr—— 径向力，

M—— 力矩。

3 球轴承刚度计算

如图 1 所示，单个球在外部载荷Q作用下，内、外滚道沟曲率中心之间的距离s将随着滚道之间的法向趋近量而变化，具体如式（1）、（2）所示[3]。

图1 球-滚道接触

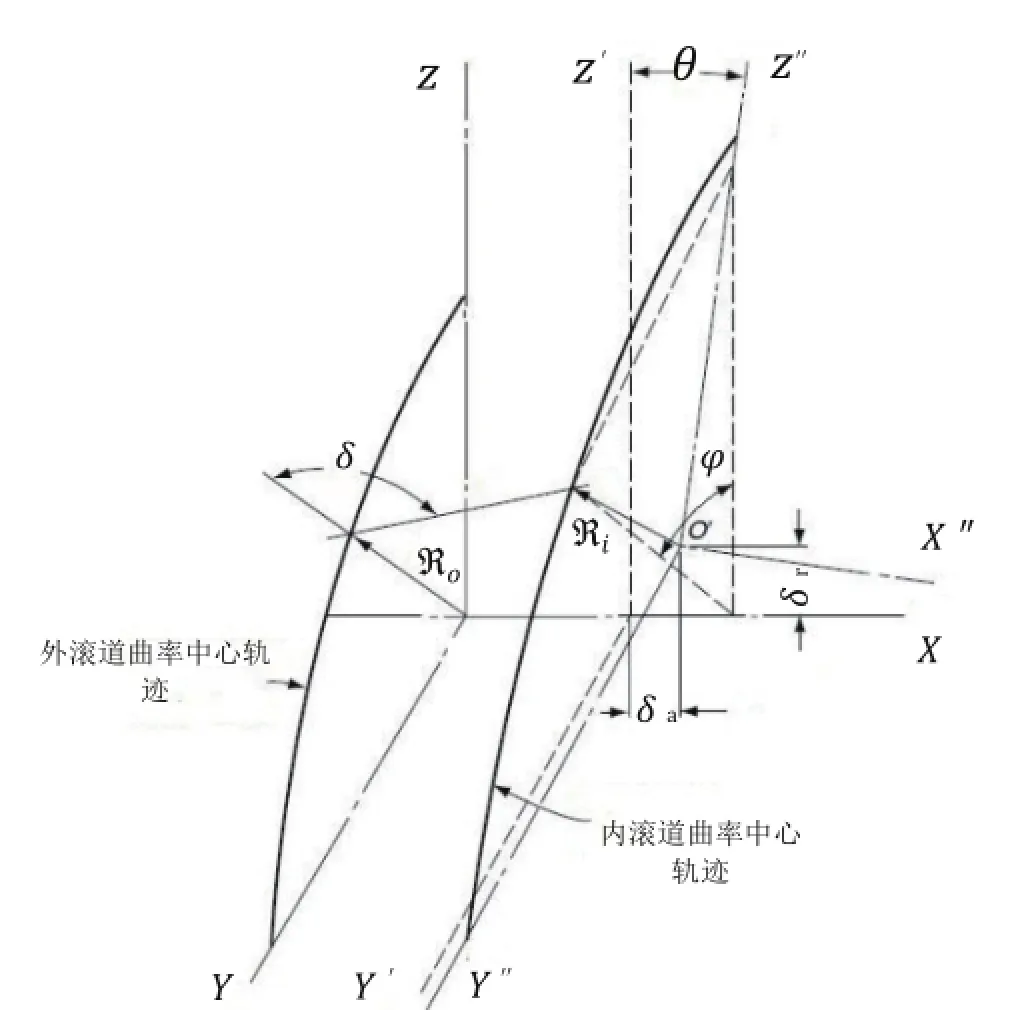
图2 载荷作用后沟曲率中心轨迹

对于球轴承而言，当其受到外部的轴向力Fa、径向力Fr以及倾覆力矩M后，轴承内、外滚道将产生相对轴向位移δa、相对径向位移δr以及相对角位移θ，如图 2 所示，如果认为轴承外圈在空间上是固定的，那么在任意滚动体位置处，内外圈沟曲率中心之前的距离s表达式如下[3]：

将式（3）代入式（2）可得：

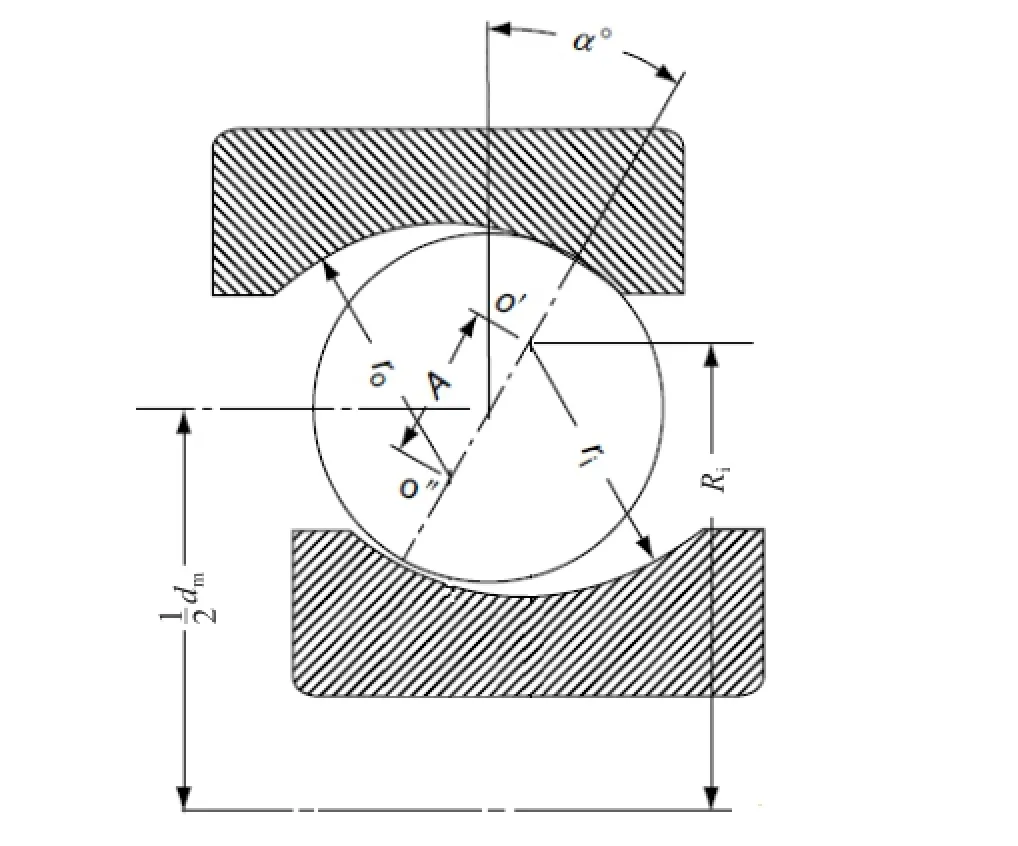
图3 内沟曲率中心轨迹半径示意图

式中，Ri为内滚道沟曲率中心轨迹半径，具体如图（3）所示，由图可得其计算表达式如式（5）所示：

结合滚动体-滚道接触的载荷与位移关系（6），即可得到单个滚动体作用于滚道上法向载荷的计算方程。

在具有多个滚动体的球轴承内，可列静力平衡方程如下[3,4]：

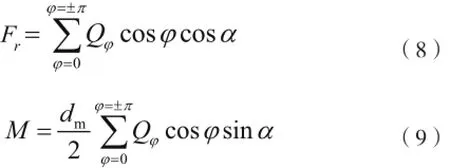
其中α为工作接触角，可由式（10）确定。

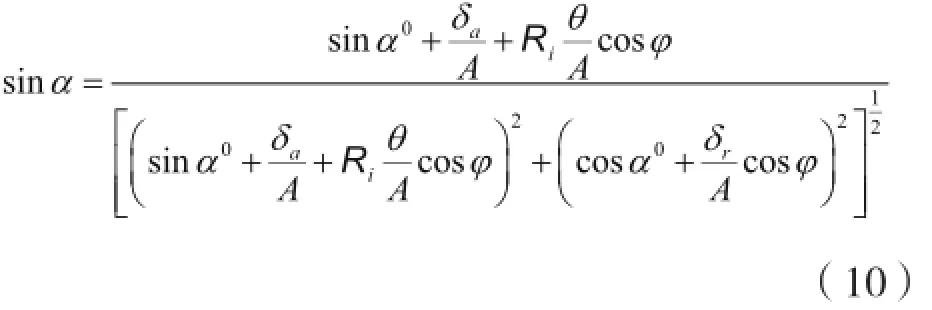
联立（7）、（8）、（9）式求解并对位移进行求导，即可求得内、外滚道间的相对位移和各方向的刚度，可通过Newton-Raphson法进行求解，刚度矩阵解析表达式如式(11)所示。

4 结果分析

以7005角接触球轴承为例进行计算分析，轴承参数如表 1 所示，下文从四个方面对具有不同接触角的轴承(其余参数均相同)进行了对比分析，分别为轴向力与轴向位移、轴向力与轴向刚度、轴向力与径向刚度、刚度比(径向刚度/轴向刚度）。

4.1 轴向力—轴向位移

图4 为角接触球轴承轴向力与轴向位移关系图，从图中可以看出：

（1）在相同轴向力作用下，轴承自由接触角越大，其轴向位移越小；以轴向力为160N为例，15°、18°、25°、30°、35°、40°、45°接触角轴承的轴向位移分别为：10.3μm、8.1μm、5.1μm、3.9μm、3.2μm、2.6μm、2.2μm；

（2）在相同接触角情况下，轴向力越大，其轴向位移越大；在轴向力由0升至640N过程中，15°、18°、25°、30°、35°、40°、45°接触角轴承的轴向位移分别由0增至22.1μm、18.2μm、12μm、9.5μm、7.8μm、6.5μm、5.6μm。

4.2 轴向力—轴向刚度

图5 为角接触球轴承轴向力与轴向刚度关系图，从图中可以看出：

表1 7005轴承参数

图4 轴向力 — 轴向位移

图5 轴向力 — 轴向刚度

（1）在相同轴向力作用下，轴承自由接触角越大，其轴向刚度越大；以轴向力为160N为例，15°、18°、25°、30°、35°、40°、45°接触角轴承的轴向刚度分别为：26.8N/ μm、32.6 N/μm、49.1 N/μm、62.8 N/μm、77.4 N/μm、92.4 N/μm、107 N/μm；

（2）在相同接触角情况下，轴向力越大，其轴向刚度越大；以15°角接触球轴承为例，当轴向力为10N、20N、40N、80N、160N、320N、640N时，其轴向刚度分别为：8.3 N/μm、10.9 N/ μm、14.4 N/μm、19.4 N/μm、26.8 N/μm、38 N/μm、55.5 N/μm。

4.3 轴向力—径向刚度

图6 为角接触球轴承轴向力与径向刚度关系图，从图中可以看出：

（1）在相同轴向力作用下，轴承自由接触角越大，其径向刚度越小；如在160N轴向力作用下，15°、18°、25°、30°、35°、40°、45°接触角轴承的径向刚度分别为：130 N/ μm、121 N/μm、101 N/μm、87.6 N/μm、75.1 N/μm、63.4 N/μm、52.4 N/μm；

（2）在相同接触角情况下，轴向力越大，其径向刚度越大；如在15°接触角情况下，当轴向力为10N、20N、40N、80N、160N、320N、640N时，其轴向刚度分别为：53.9 N/μm、67.7 N/μm、84.6 N/μm、105 N/μm、130 N/μm、158 N/μm、192 N/μm。

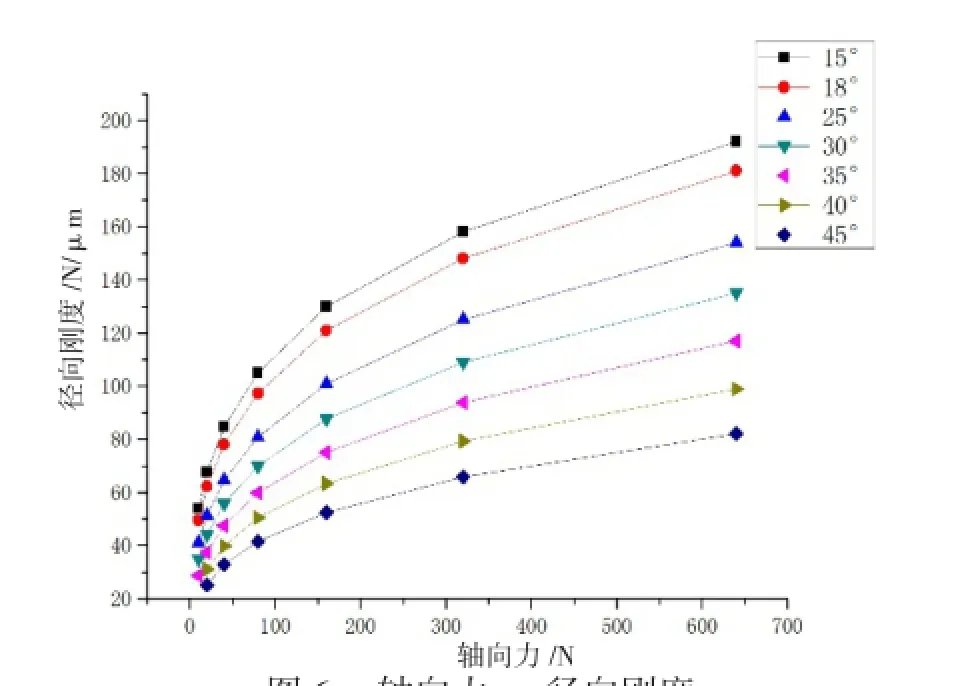
图6 轴向力 — 径向刚度

4.4 刚度比值

图7 为角接触球轴承径向刚度与轴向刚度比值关系图，从图中可以看出：

图7 刚度比(轴向刚度/径向刚度）

（1）在相同轴向力作用下，轴承自由接触角越大，其刚度比值越小；如在160N轴向力作用下，15°、18°、25°、30°、35°、40°、45°接触角轴承的刚度比值分别为：4.8、3.7、2.1、1.4、1.0、0.7、0.5；

（2）在相同接触角情况下，轴向力越大，其比值越小；如在15°接触角情况下，当轴向力为10N、20N、40N、80N、160N、320N、640N时，其刚度比值分别为：6.5、6.2、5.9、5.4、 4.8、4.2、3.5；

（3）接触角越小，刚度比值变化范围越大，在轴向力由10N升至640N过程中，15°接触角轴承的刚度比值由6.5降至3.5，18°接触角轴承的刚度比值由4.5降至2.9，25°接触角轴承的刚度比值由2.3降至1.8，30°、35°、40°和45°接触角轴承的刚度比值相对稳定，分别为1.4、1.0、0.7和0.5，变化较小。

5 结束语

角接触球轴承的刚度与其所受轴向力呈非线性的对应关系，并且与轴承内部参数密切相关，故在讨论轴承的刚度问题时，必须明确指出其所受轴向力的大小，而对于其内部参数，则需要通过轴承厂商进行获取。

研究表明，对于仅接触角不同(其它参数完全相同)的角接触球轴承而言，在相同轴向力作用下，轴承自由接触角越大，其轴向刚度越大，但轴向位移、径向刚度以及刚度比值(径向刚度/轴向刚度)都越来越小；在相同接触角情况下，轴向力越大，其轴向位移、轴向刚度和径向刚度都越来越大，但其刚度比值(径向刚度/轴向刚度)会越来越小。

本文的研究对轴承预紧力的选择也有重要的指导意义，用户可根据所需的轴承刚度，对轴承的预紧力进行调节。目前，各大轴承厂商会在其发行的轴承样本中指出各自轴承所需的预紧力及对应刚度，这为常规轴承的恰当使用提供了方便，但对于非常规轴承的研究和使用，本文提供了有效的研究方法。

[1] 陈时锦,张春玉. 轴承刚度矩阵的解析推导与计算机求解[J]. 轴承,2006(2)：1-4.

[2] 李忠杰,王树宗. 角接触球轴承刚度矩阵的理论推导与计算[J].轴承,2007(9)：1-3.

[3] Harris T A, Kotzala M N. 滚动轴承分析［M］．罗继伟，马伟，杨咸启，等译．北京：机械工业出版社，2010.

[4] 万长森．滚动轴承的分析方法［M］．北京：机械工业出版社，1987.

（编辑：王立新）

Study on stiffness of angular contact ball bearing

Aiming at the relationship among contact angle, axial force and stiffness of angular contact ball bearing, the paper studies the stiffness of the bearings with different contact angles (the other parameters are same) by establishing the static equilibrium equation. Research shows that, under the same axial force, the bigger the free contact angle is, the bigger the axial rigidity is, but the axial displacement, radial stiffness and stiffness ratio (radial stiffness / axial stiffness) are getting smaller. Under the same contact angle, when the axial force is bigger, the axial displacement, the axial stiffness and the radial rigidity will be greater, but the stiffness ratio will be smaller..

angular contact ball bearing; contact angle; axial force; stiffness

TH133.33+1

A

1672-4852（2017）01-0008-04

2017-03-03.

张振强（1987- ），男，工程师.

河南省重大科技专项《机器人专用轴承关键技术研究及产业化》(161100210800 ).

Zhang Zhenqiang1,2,3, Wang Dongfeng1,2,3, Zhou Haibo1,2,3

(1.Luoyang Bearing Science & Technology Co.,Ltd.,Luoyang 471039, China; 2.Henan Key Laboratory of High Performance Bearing Technology,Luoyang 471039,China; 3. Strategic Alliance for Technology Innovation in Rolling Bearing Industry,Luoyang 471039,China )