基于多元回归模型的风电场费用分析与应用

王 铮

（华北电力大学 中国北京 102206）

基于多元回归模型的风电场费用分析与应用

王 铮

（华北电力大学 中国北京 102206）

本文以线性多元回归模型为理论基础，通过对30个规模相同的风电机组概算数据进行采集、按占比大小进行排列的方法，提取出30个样本中的四项特征费用。针对这四项费用，利用SPSS软件模拟出与概算总额的关系，随后通过统计学三大检验的方法共同论证该模型的科学性与可靠性，达到节约成本、提高概算水平的目的。

多元回归模型；风电费用分析

随着我国经济的快速发展和生活水平的提高，电能越来越成为生产生活必不可少的产品，小到日常生活，大到国家产业，电能的消耗几乎已经成为每一个人工作和生活的必要环节，人们在享受其带来便利的同时，电力紧缺、火电厂环境污染等一系列问题也逐渐暴露出来。即使在人民环保意识逐渐高涨的今天，这些问题依然没有得到解决。针对全社会用电量提高，发电所用的煤炭逐年减少且存在着环境污染的问题，国家也出台了一系列措施。本文利用计量经济学中的多元回归方程模型，通过对费用构成中主要费用的提取与分析多元回归模型，随后依据统计学原理的相关知识对模型进行检验，最后运用模型预测风电场的总造价，利用这种方法不仅减小概算预测的工作量，同时可以提供总造价的参考范围，为造价控制奠定基础。

1 多元回归模型的原理

多元线性回归是对未来的电力负荷进行定量预测的一种方法 (即通过对影响因子和用电量的历史数据进行分析，确定用电量和影响因子之间的关系,求出对应预测点的预测值和预测置信区间(回归分析法采用原始数据建模，适用于大样本。

多元线性回归的数学模型一般表示为：

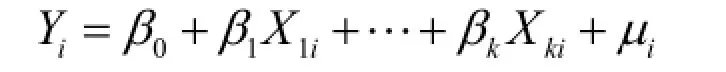
其中：β0为常数项，β1 ,… βk为偏回归系数，μi为随机误差项

它被解释变量的变化由两部分进行解释(第一，由解释变量的变化引起的线性变化部分； 第二，由其他随机因素引起的变化部分。多元线性回归通过确定回归方程中的解释变量( 自变量) 和被解释变量( 因变量) (确定回归模型&建立回归方程&对回归方程进行拟合优度检验和显著性检验&回归系数的显著性检验&残差分析等过程完成。具体操作步骤如下

（1）收集数据：数据是多元回归的基础，只有以良好的数据资料为统计基础才能建立出有效的模型，经过验证后才更加真实与客观。（2）拟合与检测模型：利用SPSS软件对数据结果实行拟合操作，得到模型的结果，但是模型的结果是否准确，则需要进一步的验证。在多元回归方程中，检测主要从三个方面进行，以下对这三个方面进行论述：

a经典假设检验：检验的主要内容是共线性、序列相关、异方差、正态分布，如果假定不成立，OLS估计量不再有效，回归分析的统计检验结果再显著也不能说明问题。因为残差平方和中既有观测误差，又有模型误差，t，F检验的p值再小，也不意味模型正确。b统计检验：从统计性质上已知，对无偏估计量，如果有足够多的重复抽样，参数估计值的期望（均值）就等于其总体的参数真值，但一次抽样，估计值不会等于该真值。c经济意义检验：对于有实际意义的经济模型，应继续检测各参数上经济含义是否准确，是否与已知定理和定义相符。

综上，只有通过三步检验之后，该模型才具有科学性和说服力，在实际生产生活问题中利用该模型加以解决才具有较大的使用价值。

（3）模型应用：经过检验的模型基本已经具有了较好的拟合性质，因此在实际问题中只需要将相对应的参数分别代入方程之中就可以得到待测数据。

2 基于多元回归模型的风电场费用分析实证

为了合理估计陆上风电场的总费用，有必要将风电场的费用构成理解，在本文中所有案例都以“25台机组，每台规模为2500kw”作为标准技术方案进行讨论。根据回归方程的相关原理，按以下步骤进行操作：

（1）数据收集：

从已有项目中收集符合“25台机组，每台规模为2500kw”技术要求的工程，根据统计学要求30个工程已经可以满足较好的统计学性质，故本文的样本数目确定为30个，收集到数据后将这30个已完工数据的四张概算费用分表中抽取比重最大的分项费用,根据上述原则选择的自变量分别为施工辅助工程费、发电厂设备及安装工程费、发电厂工程费以及项目建设管理费。因变量为概算总额，具体数值如表3-1所示

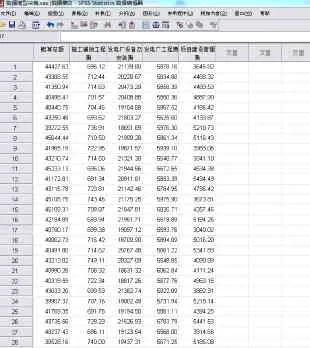
表3-1 基础数据汇总表（部分）

（2）经典假设检验

首先对于这30个数据进行经典假设检验，依照回归方程的检验原理，分别对模型进行拟合优度检验，共线性检验、序列检验和异方差检验。根据SPSS输出的结果，模型如下所示

其中y表示概算总额，x1表示施工辅助工程x2表示发电厂设备及安装费x3表示发电厂工程费x4表示项目建设管理费

A 拟合优度检验。拟合优度的检验结果见图3-2所示。

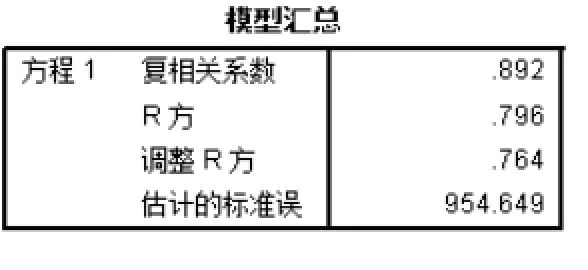
图3-2 拟合优度检验结果图

图3-3 模型的DW检验

图3-2表明，拟合优度检验结果中调整后R2的结果为0.764，说明拟合优度较好，超过四分之三的工程都可以利用该模型进行分析，不宜过分注重该指标的绝对大小，而是根据经济检验等后续检验进一步判断其拟合的效果。

B 共线性诊断。从共线性诊断分析可以看出，在五个维数中没有任何两个变量的方差比例同时接近于1，这说明在该模型中不存在高度共线的两个变量，因此该模型通过了共线性检验。

C DW检验。该模型的DW检验结果如图3-3所示，根据检验结果不难发现，DW指标为2.414，在2左右浮动，因此可以判断，该模型中不存在序列相关。故本模型通过了序列检验。

D 残差散点图。通过对模型的残差散点图分析可以看出残差散点图分布均匀没有规律，因此该模型不存在异方差。

（3）统计检验

根据统计学原理，在统计检验阶段应完成两种检验：方程整体的显著性检验以及方程中各个系数的t检验。

从上可以看出对于该模型中的五个变量的显著性水平存在着明显差异，其中常数项、发电厂设备及安装费、项目建设管理费两项费用的显著性水平极低，这两项费用和方程的常数项对该模型的影响十分显著，施工辅助工程费和发电厂工程费这两项费用的显著性水平也在允许的0-0.1以内，也就是说在统计认可的范围内这两项费用参数对模型的影响也是十分显著的，五个变量的参数值都较为准确，该模型不需要修正。

（4）经济意义检验

根据统计学原理，多元线性回归方程每一个变量的系数表示的是偏回归系数，偏回归系数是旨在解释其他变量不变的情况下，该系数所对应的变量每变化1个单位，因变量对应的变化情况。在本文的模型中，施工辅助费、设备及安装工程费、发电厂工程费的增加都表示该工程对应的设施、机组、建筑工程的数量增加，则对应的费用成上升趋势，而项目建设管理费则是受到管理水平高低影响的，管理水平越好则对应的各个表中的分项费用减少，对于风电工程来说，良好的管理可以有效降低工程实际发生的费用。

3 模型的应用

根据上述分析得出，技术指标为“25台，2000KW”机组的风电场最终的模型为：

本模型适用于每张概算表中的大体费用，但是其他占比较小的分项费用却较难统计的风电工程中，在实际应用的过程中只需明确四个变量的数值就可以概算费用的大体情况，同时还可以根据工程的规模对估计的结果值进行调整。另外，模型所给定的预测值只是一个参考值，在实际工作中工程造价人员必须依据设计和现场情况，科学客观的给出造价水平。

本文通过30个规模相同风电机组的费用，构造了四个特征费用以及常数项对概算总额影响的模型，另外利用SPSS软件，通过对该模型的经典假设检验、统计检验、经济学检验三大方面共同论证了该模型的科学性与可靠性，因此分析的结果利用价值较高，对节约社会成本、提高概算预测的效率有重大的意义。

[1] 李慧兰.我国风电发展现状及前景展望[J].科学之友,2013,11：111-113

[2] 王勇.风电工程建设中的管理模式及风险因素分析[J].产业,2014,9：34-37

[3]何秀丽.多元线性模型与岭回归分析[D].华中科技大学,武汉,2005：8-9.

TU43

B

1007-6344（2017）05-0194-02

李道明(1983.4--)，男(汉族)，广州增城人，大专，毕业于广州大学，助理工程师，目前从事桥梁隧道检测工作。

作者简介：王铮（1992-），男，宁夏回族自治区银川市，华北电力大学，学士学位，研究方向：管理科学与工程。