高坝消力戽消能跃后共轭水深的计算
2017-05-18李水泷黄朝煊
李水泷,黄朝煊
(浙江省水利水电勘测设计院 围垦院,杭州 310002)
高坝消力戽消能跃后共轭水深的计算
李水泷,黄朝煊
(浙江省水利水电勘测设计院 围垦院,杭州 310002)
针对现有高坝消力戽消能计算十分繁琐的问题,考虑底挑圆弧离心力对收缩水深的影响,基于无量纲化理论、水力学基本理论和数学理论推导,给出了高坝消力戽消能计算基本方程。利用一元三次方程的卡当公式解分别给出了坎底收缩水深和跃后共轭水深的解析计算公式,并采用MatLab计算软件对跃后共轭水深与无量纲单宽流量、无量纲总水头以及消力戽底坎挑角的影响关系进行了计算研究。最后通过工程实例计算比较,认为推导的坎底收缩水深和跃后共轭水深计算式精度可靠,方便快捷,便于工程实际应用。
高坝消力戽;消能计算;MatLab计算软件;坎底收缩水深;跃后共轭水深
1 研究背景
消力戽是指在泄水建筑物末端建造的一个具有较大反弧半径和挑角的低鼻坎,在一定下游水深时,从泄水建筑物下泄的高流速水流,受下游水位的顶托作用在戽斗内形成漩滚,主流沿鼻坎挑起,形成涌浪并向下游扩散,以达到水力消能的效果,减少水流对下游河床及堤岸的冲刷影响。
鉴于现有消力戽底流消能计算公式[1]中收缩水深的计算未考虑急变流离心力的影响,特别对于高坝,由于总水头较大,其底坎收缩水深一般较大,底坎圆弧离心力对收缩水深的雍高影响较明显,因此,对于高坝必须考虑离心力对收缩水深的影响。梁曾相[2]和田忠等[3]对急变流的水力学计算进行了研究,但计算方程为高度非线性方程,对于一般工程设计人员而言,精确求解计算具有一定困难;程飞等[4-5]采用有限元软件对微挑消力池进行了数值模拟,得出了底挑参数对消能的影响关系,但未能给出计算通式;程飞等[6]根据水力学能量方程建立了微挑消能基本方程,给出了相应迭代算法,但计算较繁琐,且未考虑底挑后跌坎的水力影响;黄朝煊等[7]对矩形断面消力池消能计算进行了研究,给出了最不利工况下池深极值的计算式;王贺瑶等[8]就底挑消能离心力对坎底收缩水深的影响进行了初步研究;黄朝煊等[9-10]对扩散型梯形断面消力池消能计算进行了深入研究。但目前与消力戽消能解析计算研究相关的文献相对较少。
基于以上研究成果的不足,本文基于无量纲化理论、水力学基本理论以及数学理论推导,采用MatLab计算软件对高坝消力戽消能计算进行深入研究,以便于工程实际应用。
2 消能计算基本方程
依据水力学理论,消能工的消能基本计算式为:
(1)
(2)
式中:d为消力池池深(m);σ0为水跃淹没系数,可取1.05~1.10;h2为跃后水深(m);ht为下游水深(m);Δz为出池落差(m);α为水流动能校正系数,可取1.00~1.05;q为过流单宽流量(m2/s);g为重力加速度常数(m/s2);φ为出流流速系数,可取0.95~1.0。其中跃后水深h2将在后文给出计算式,下游水深ht可根据明渠流理论计算,如黄朝煊[11]对梯形明渠的临界水深、正常水深等特征水深给出了高精度计算式。
3 消力戽消能特征水深计算
3.1 坎底收缩水深计算
根据能量原理,消力戽坎底急变流处的能量方程如式(3)所示。
(3)
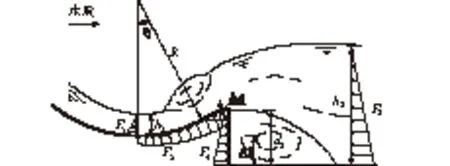
式中:Q为流量(m3/s);A0,z0,p0,v0,α0分别为起始断面的断面面积(m2)、高程(m)、水压(m)、流速(m/s)以及水流动能修正系数;参数A,z,p,v分别为计算断面的断面面积(m2)、高程(m)、水压(m)、流速(m/s);γ为流体的重度(kN/m3);h损为水头损失量(m)。高坝消力戽消能示意图见图1。
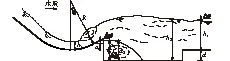
图1 高坝消力戽消能示意图Fig.1 Schematic of bucket energy dissipation for high dam
图1中参数θ为底坎挑角(°);Δa为底坎圆弧挑段后的直线延长段的高差(m);Δb为底坎的坎底最低点与消力池池底之间的高差(m);a1为底坝延长段最高点与坝底的高差(m);a2为底坎延长段最高点与消力池池底的高差(m);d为消力池池深(m);R为坎底圆弧半径(m);h1为坎底处收缩断面水深(m)。
根据积分理论推导[3]可知,坎底凹曲面对能量方程影响附加项可表示为
(4)
其中Ko为离心力附加影响系数,其计算式为
当坎底为平面时,即坎底半径R→∞,离心力附加影响系数Ko=0,此时便退化为一般的明渠消能。
根据坎底圆弧收缩水深计算理论,考虑离心力对收缩水深的雍高影响,则有
(5)
式中T0为以收缩断面底部为基准面的泄水建筑物上游总水头(m)。
通过MatLab软件数值分析,离心力附加影响系数可采用高精度等效函数简化为
(6)
通过MatLab软件数值分析,认为式(6)对于h1/R<0.6时,式(6)相关系数>0.99,最大相对误差<1.5%,精度完全满足工程实践要求。图2为精确值与式(6)拟合值对比图。
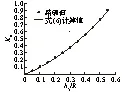
图2 式(6)精度对比Fig.2 Precision of formula (6)
(7)
根据一元三次方程的卡当公式解理论,可得坎底无量纲收缩水深计算式为
(8)
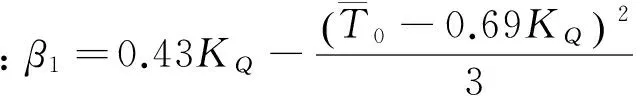
进而可得坎底水流的弗劳德数简化计算式为
(9)
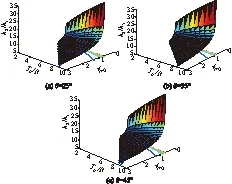
根据文献[1]案例资料及相关工程设计经验可知,通常情况下参数取值满足以下范围:2.0 图3 坎底挑流消能水力参数与KQ,T0/R的关系曲面Fig.3 Relations of hydraulic parameters vs.KQ and T0/R 3.2 消力戽消能共轭水深计算 对于消力戽消能的跃后共轭水深(见图4)的计算,本文利用连续方程和动量方程,通过推导可得水跃方程式为 (10) 式中:v1,v2为跃前断面和跃后断面平均流速(m/s);α1,α2分别为跃前断面和跃后断面流速系数;F1,F2分别为跃前断面和跃后断面顺水流轴线方向作用力(m2);F3为坎底圆弧沿轴线方向作用力分量(m2);F4为消力戽挑坎后水垫池内壁在顺水流轴线方向的作用力分量(m2)。 图4 消力戽消能水力计算简图Fig.4 Schematic of hydraulic calculation for energy dissipation of the bucket (11) 式中:β为消力戽内离心力修正系数,可近似取1.0;hθ,vθ,Kθ分别为坎上水深、流速和修正系数随角变量θ变化的函数;P直段为坎底直线段水平反力分量。 (12) (13) 记 (14) 同样根据一元三次方程的卡当公式,相对跃后共轭水深的解为 (15) 本文分析了参数Δa/R=0.1,Δb=0时,相对跃后共轭水深η=h2/h1与无量纲总水头T0/R、无量纲单宽流量KQ以及底坎挑角θ的关系,见图5。 图5 h2/h1与KQ,T0/R的关系曲面Fig.5 Relationship among h2/h1 and KQ, T0/R 由图5可知: (1) 无量纲总水头T0/R越大、无量纲单宽流量KQ越小,则相对跃后共轭水深η=h2/h1(跃后共轭水深与跃前收缩水深的比值)越大。 (2) 在无量纲单宽流量KQ固定不变的情况下,相对跃后共轭水深随无量纲总水头T0/R在一定区间内呈近似线性增长关系变化。 (3) 无量纲总水头T0/R固定不变的情况下,相对跃后共轭水深随无量纲单宽流量KQ在一定区间内呈近似双曲线衰减关系变化。 (4) 无量纲总水头T0/R、无量纲单宽流量KQ固定不变的情况下,相对跃后共轭水深随底坎挑角的增大而稍有增大。 某重力坝底挑圆弧半径R=20 m,假设总水头T0=65.4 m,单宽流量q=74.08 m2/s,底坎挑角θ=35°,Δa/R=0,Δb/R=0,试求跃后共轭水深h2以及坎后水垫消力池池深d。 鉴于现有高坝消力戽消能计算十分繁琐的问题,考虑底挑圆弧离心力对收缩水深的影响,基于无量纲化理论、水力学基本理论以及数学理论推导,并结合MatLab计算软件对高坝消力戽消能计算进行了研究,主要结论如下。 (1) 根据无量纲化理论、水力学基本理论以及数学理论推导,给出了高坝消力戽消能计算基本方程,利用一元三次方程的卡当公式解分别给出了坎底收缩水深以及跃后共轭水深的解析计算公式,便于工程实际应用,比以往通常的试算法更方便快捷。 (2) 采用MatLab计算软件对跃后共轭水深与无量纲单宽流量、无量纲总水头以及消力戽底坎挑角的关系进行了计算研究,给出不同底坎挑角θ(25°,35°,45°)下相对跃后共轭水深η=h2/h1与无量纲总水头T0/R、无量纲单宽流量KQ之间的三维关系曲面。最后通过工程实例计算比较,认为本文推导的坎底收缩水深和跃后共轭水深计算式精度可靠,方便快捷,便于工程实际应用。 [1] 中华人民共和国水利部. 水工设计手册( 第二版)(第七卷)[M]. 北京:中国水利水电出版社,2011:377-476.[2] 梁曾相. 恒定急变流的能量方程及其应用 [J]. 水利学报, 1982,27(2): 32-38. [3] 田 忠,王 韦,刘善均,等. 曲面急变流水面线及床面压力的计算 [J]. 四川大学学报(工程科学版), 2002, 34(6): 43-46. [4]程 飞, 刘善均. 微挑消力池的数值模拟与试验研究 [J]. 四川大学学报(工程科学版), 2011,43(增1): 12-17. [5] 程 飞,白瑞迪,刘善均,等. 数值模拟对比研究微挑消力池水力特性 [J]. 水力发电学报, 2012, 31(2): 71-78. [6] 程 飞, 杨朝晖, 刘善均. 底挑消能工共轭水深的优化计算与试验研究[J]. 水力发电学报, 2014,33(3): 189-194. [7] 黄朝煊, 王贺瑶, 王正中,等. 消力池最不利条件下池深极值探讨[J]. 水力发电学报, 2015,34(1): 79-84. [8] 王贺瑶, 黄朝煊. 考虑离心力非线性影响的高坝底挑消能收缩水深解析算式研究[J]. 安徽农业科学, 2015, 43(23):344-345. [9] 黄朝煊. 梯形断面消力池扩散型消能计算[J]. 水利水电科技进展, 2016,36(5): 34-39. [10]黄朝煊,方咏来,李水泷. 扩散型梯形翼墙消力池最不利消能工况计算研究[J]. 长江科学院院报, 2017,34(1): 71-76. [11]黄朝煊. 梯形明渠水力学特征水深的解析计算式研究[J]. 灌溉排水学报, 2016,35(3): 73-77. (编辑:刘运飞) Calculation of Conjugate Water Depth of EnergyDissipation for High Dam LI Shui-long, HUANG Chao-xuan (Department of Reclamation, Zhejiang Provincial Water Conservancy and Hydropower Survey and Design Institute, Hangzhou 310002,China) In view that the calculation of energy dissipation bucket for high dam is very complicated, the influence of centrifugal force of bottom arc on the contraction of water depth is considered in giving basic equations of energy dissipation based on the theory of dimensionlessness, the basic theory of hydraulics and the derivation of mathematical theory. Equations of the contracted water depth at the bottom of bucket and the downstream conjugate water depth are given respectively by using the Cardan formula of simple cubic equation. Moreover, MatLab software is used to calculate the relationship among conjugate water depth and dimensionless discharge per unit width, dimensionless total head and bucket angle. Calculation and comparison on engineering examples proves that the proposed equations for bottom contracted water depth and downstream conjugate depth are accurate, reliable and convenient to be applied to practical project. roller bucket of high dam; energy dissipation calculation; MatLab; bottom contraction water depth; conjugate water depth after jump 2016-02-25; 2016-07-08 水利部公益性行业科研专项项目(201401010);浙江省水利水电勘测设计院科标业资助项目(B1608,B1609) 李水泷(1978- ),男,浙江临安人,高级工程师,主要从事水利工程设计,(电话)13867422505(电子信箱) 544309276@qq.com。 黄朝煊(1983- ),男,湖北黄石人,工程师,硕士,主要从事水工结构及岩土工程设计与研究,(电话)13819483276(电子信箱) 516227811@qq.com。 10.11988/ckyyb.20160147 2017,34(5):44-47,57 TV131.4 A 1001-5485(2017)05-0044-04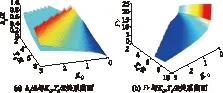
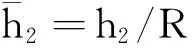
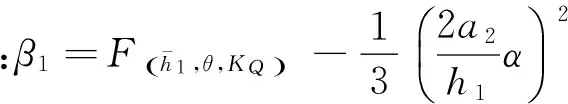
4 算例分析
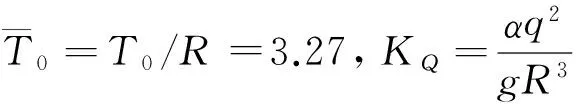
5 结 语
