基于层次分析法的茂县斜坡地质灾害易发性评价
2017-05-18刘宇恒熊倩莹
刘宇恒,邓 辉,熊倩莹
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室,成都 610059)
基于层次分析法的茂县斜坡地质灾害易发性评价
刘宇恒,邓 辉,熊倩莹
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室,成都 610059)
茂县是西南深切河谷地区地质灾害的重灾县之一,亦是对区域地质灾害进行特征分析及易发性评价的良好试验基地。在茂县斜坡地质灾害详查及遥感数据解译的基础上,选取高程、地形起伏度、坡形、坡度、地层岩性、水系因子及地质构造7个因素作为评价指标,采用层次分析法对研究区斜坡地质灾害易发性进行评价与区划。结果表明:地质灾害高易发区占地面积约46.1 km2,占10.02%,主要分布于研究区的岷江干流沿岸及其部分支流沿岸等;中易发区面积约149.59 km2,占32.52%;低易发区面积约205.25 km2,占44.62%;非易发区面积约59.06 km2,占12.84%。评价结果与野外调查基本吻合,可为茂县斜坡地质灾害防治及土体规划利用提供依据。
斜坡地质灾害;易发性评价;四川茂县;地理信息系统;层次分析法
1 研究背景
四川省茂汶羌族自治县地处西南深切河谷地区,境内自然地质背景环境特殊,地质构造复杂,新构造运动活跃,河谷强烈侵蚀切割,各种滑坡、崩塌等斜坡地质灾害普遍发育。尤其在2008年5月12日汶川地震之后,斜坡地质灾害的发生越来越多,茂县人民的生命财产安全受到很大威胁。由此可知,进行地质灾害调查和评价工作,科学分析地质灾害的易发性,对茂县斜坡地质灾害的预防和减轻具有深远意义。
合理评价地质灾害易发性十分重要,近年来许多专家学者对此进行了大量研究[1-8],但在对评价地质灾害易发性的方法选择上一直没达成共识。由于层次分析法简易、灵活且逻辑性和实用性较强,已是一套较为成熟的方法,因此,本文基于层次分析法,对茂县区内斜坡地质灾害易发性进行评价。
2 研究区概况
茂汶羌族自治县位于四川省西北部,是阿坝藏族羌族自治州下辖县,地理坐标在31°24′N─32°17′N, 102°56′E—104°10′E之间,南北宽约94.8 km,东西长约116.5 km,占地面积约3 885.6 km2。研究区遥感图如图1所示。
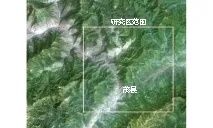
图1 研究区遥感图Fig.1 Remotely-sensed image of the research area
茂县属于亚热带季风气候,多年年平均降水量为484.1 mm,容易出现冬干春旱的现象。县境内地质结构较为繁杂,大部分属于马尔康地质分区,其东南部的狭窄部分属于龙门山地质分区。区内岩土体类型主要由夹沙灰、黑色页岩、砂板岩及火成岩等组成。土壤主要为暗棕壤、褐土、棕壤。研究区地处龙门山地震地段,是中国地震频繁的地区之一。岷江从北往南纵贯全县,黑水河、赤不苏河及松坪河分别在大、小两河口与较场乡汇进岷江,土门河自西往东贯穿土门全区,汇进涪江水系。这种奇特的区域地质环境与频繁的内外动力地质条件,使得研究区内深切河谷斜坡地质灾害十分发育,且灾害类型以滑坡、崩塌为主。经现场调查,斜坡地质灾害总共147处,其中滑坡灾害有98处,约占总数的67%,其他为崩塌灾害,共有49处,约占总数的33%,分布统计见表1。

表1 茂县斜坡地质灾害分布统计Table 1 Statistics of slope geo-hazard distribution in Maoxian county
3 茂县斜坡地质灾害易发性评价
3.1 层次分析法简介
层次分析法是一种把定性的问题进行定量化分析的多重准则决议方法,其特点是将一个复杂的问题分解成一系列有序层次的组成因素,再将专家的主观经验与研究区地质环境特征基于一定客观化的判别矩阵联系起来,使用数学运算方式定量地描述各层中影响因子的相对重要程度,并赋予其对应的权重值,最后根据全部影响因子相对总目标的相对权重值进行排序。
本文尝试采用层次分析法来建立斜坡地质灾害评价因子的递阶层次结构,构造两两评价因子比较的判断矩阵,给予其相对应的权重值且进行一致性检验,再计算各层因素的组合权重[9]。
3.2 评价因子的选取
为突出研究区斜坡地质灾害发生的主要影响因素,结合前人的研究成果,根据研究区内地质环境特征与斜坡地质灾害的分布规律及形成条件,选取地形地貌(包括高程、地形起伏度、坡形及坡度)、地层岩性、水系因子及地质构造7个因素作为评价因子。
其中,在评价因子原始数据提取时,基于野外详查,利用GIS软件空间分析中的表面分析功能从DEM数据中提取出高程;利用ArcGIS软件的邻域分析功能,得到一定区域内最低海拔与最高海拔的差值,作为中心栅格的地形起伏度;把剖面曲率值≤-0.5的归为凹型坡,-0.5<剖面曲率值≤0.5的归为直线型坡,剖面曲率值>0.5的归为凸型坡;在GIS系统中利用缓冲分析工具,以河流为中心建立缓冲区,根据距离构造断裂带的远近关系,以断裂为中心创建缓冲区。
碳酸盐矿物溶解过程中,生成游离态的Ca2+、Mg2+、CO2和H2O,消耗大部分矿物质,且溶液中的Na+、H+随溶液不断渗入煤体中,置换出Ca2+、Mg2+,Na+、H+。由于煤样中大部分碳酸盐矿物发生溶解和吸附,溶液中离子不断发生扩散、迁移等离子交换反应,煤样孔裂隙周围不断形成孔洞,使煤样孔隙结构改变,孔隙率增大,孔隙体积等于反应运移溶质体积。碳酸盐矿物的溶解量与煤样孔隙率之间的关系可以用以下公式表示:
3.3 层次分析法步骤
3.3.1 递阶层次结构分析模型创建
创建递阶层次结构是层次分析法的步骤中最重要的一步,必须要使同一层的各个单元附属于其对应的上一个层次的分类,且必须确定与之对应的下一层次中的每一个单元[10]。将前文中所选取的7个影响因子分类并归化,便可绘制斜坡地质灾害易发性评价的3层递阶层次结构分析模型(如图2)。其中A层为目标层,B层为准则层,C层则为措施层。
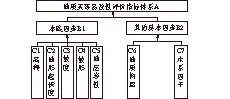
图2 层次结构分析模型Fig.2 Analytical hierarchy model
3.3.2 判断矩阵构造
在准则A的支配下按照其从属元素两两之间的相对重要程度对B1,B2,B3,…,Bn赋予其相对应的权重值。本文采用1—9标度法[10](如表2),针对各层中的要素对上一层次目标的相对重要性进行两两比较(表3至表5),进而构造判断矩阵。

表2 判断矩阵标度(重要性指标)及其含义Table 2 Scales of judgment matrixes and their connotations

表3 A-B层判断矩阵Table 3 Judgment matrixes in A-B level

表4 B1-C层判断矩阵Table 4 Judgment matrixes in B1-C level

表5 B2-C层判断矩阵Table 5 Judgment matrixes in B2-C level
3.3.3 基于判断矩阵的被比较因素相对权重的计算
运用求和法对每个两两成对比所形成的判断矩阵计算,从而可以得到与其相对应的特征向量和最大特征根近似值λmax:
(1) 对两两相比较的矩阵A中的每一列向量进行归一化处理,得到
(1)
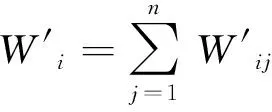
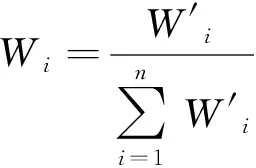
将矩阵进行一致性检验,计算公式为
(2)
其中,
(3)
式中:CR为一致性比例,只有当CR<0.1时,矩阵的一致性检验才算合格;n为两两比较的元素的个数;CI为一致性指标;RI为随机一致性指标,其值由表6确定。
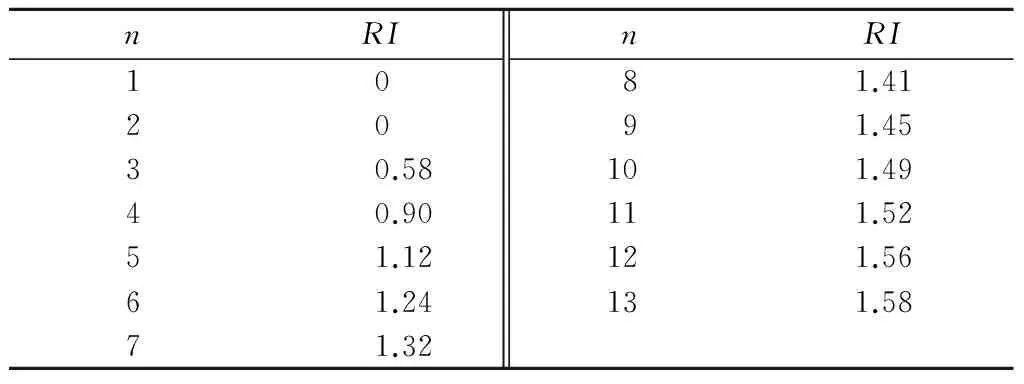
表6 随机一致性指标RI值Table 6 Numerical values of random consistent index RI
经过计算,A-B层判断矩阵的最大特征根近似值λmax=2,把最大特征向量归一化得到B1,B2评价指标的权重Wi,均为0.5。B1-C层判断矩阵λmax=5.068 3,一致性指标CI=0.017,随机一致性指标RI=1.12,则一致性比例CR=0.015 25<0.1,一致性检验合格,该矩阵具有较好的判断一致性。把最大特征向量归一化得到C1,C2,C3,C4,C5这5个影响因素的权重值Wi,分别为0.062 4,0.098 6,0.261 8,0.416 2,0.161 0。而B2-C层判断矩阵的最大特征根为λmax=2,将最大特征向量归一化得到C6,C7评价指标的权重Wi,分别为0.142 9,0.857 1。
3.3.4 组合权重计算
若要获取每一个层次中全部因素相对总目标的相对权重值,则需要计算最下层对目标的组合权向量,并根据公式做组合一致性检验,若检验通过,则可按照组合权向量表示的结果进行决策,否则需要重新考虑模型或重新构造那些一致性比率较大的成对比较阵[10]。将B1,B2层归一化处理后的权重值在A层次下再次归一化处理即可得到7项评价要素的权重总排序,如表7所示。
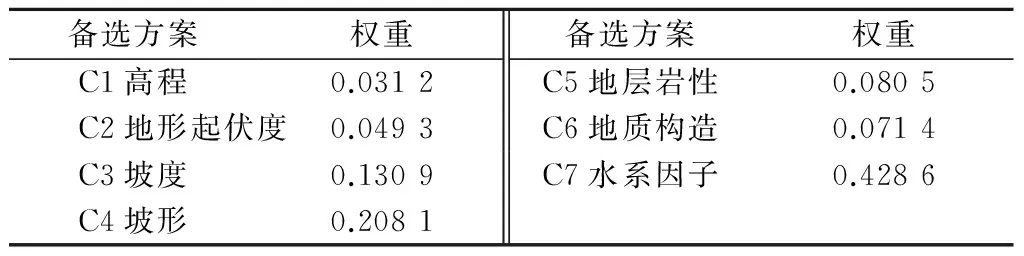
表7 组合权重结果Table 7 Result of combinatorial weights
3.3.5 层次分析法定量评分
地质灾害的易发性评价可以根据7个影响因子的权重值和打分完成,在分析评价的过程中,将每一个因子根据一定的准则进行打分,再将每一个指标因子的赋值与其相对应的权重相乘就可以求出地质灾害的易发性值R,即
(4)
式中Bi为各评价因子的定量打分。
对指标因素定量打分的准则为将7个评价因素的权重值排序。将权重因子最小的因子开始赋值为1分,权重倒数第二小的因素赋值为2分,以此类推,依次从1到7分。按照每个因素的分级准则,如果因子的测量值是最小的分级,就统一都赋值为1分,假如是属于上一个分级,就按照它所在的7个因素中的排序位置加之其相应的分值(比如,其权重值在7个因素中排在了第5位,它的评分值就赋予5分,如果测量值是属于上一个分级,就在原来的基础上加上5分),之后向上按等差级数递增[11]。但是,因为水系因子对地质灾害发生的敏感性最高,且离水系越近,地质灾害越易发生,因此,水系因子的分数从35分倒次打到1分。层次分析法定量评分结果见表8。

表8 层次分析法定量评分结果Table 8 Result of quantitative rating by AHP
为了更为简单地进行对比分析,将易发性指数归一处理化,从而得到茂汶羌族自治县幅区域地质灾害易发性评价图(图3)。
图3 层次分析法的易发性评价结果Fig.3 Result of susceptibility evaluation by AHP
3.4 斜坡地质灾害易发性区划
将层次分析法得出的区域地质灾害易发性评价结果运用等间距分级方法进行分级,得到4个易发性评价等级:高易发区(易发性指数为(0.75,1.00])、中易发区(易发性指数为(0.50,0.75])、低易发区(易发性指数为(0.25,0.50])、非易发区(易发性指数为(0,0.25])。在此基础上,结合茂县的自然地质环境如地形地貌、地质构造、岩石类型、河流流域等,考虑环境保护及治理工作规划,对上述4个易发性等级进行轻微调整,去除异常点,得出茂县区域斜坡地质灾害易发性程度分区:高易发区、中易发区、低易发区、非易发区(见图4)。

图4 茂县幅斜坡地质灾害易发性区划Fig.4 Zoning of slope geo-hazard susceptibility in Maoxian County
由图4可知,高易发区占地面积约46.1 km2,占研究区总占地面积的10.02%,主要分布于研究区的岷江干流沿岸及其部分支流沿岸等;中易发区面积约149.59 km2。占研究区总占地面积的32.52%,主要紧邻地质灾害高易发区域分布;低易发区分布密度相对较低,面积约205.25 km2,占研究区总面积的44.62%;非易发区面积约59.06 km2,占研究区总面积的12.84%。
图4斜坡地质灾害主要集中分布在河流沿岸、人类活动强烈的地区,与现场调查成果拟合度较高,可见运用层次分析法对茂县斜坡地质灾害易发性评价的结果较为理想。
4 结 论
(1) 本文基于层次分析法,建立以斜坡地质灾害易发性综合评价指数为目标层,以高程、地形起伏度、坡形、坡度、地层岩性、水系因子及地质构造7个因素作为指标层的茂县斜坡地质灾害易发性评价的层次分析模型,并确定了各基础指标层的因子对目标层的权重。其中高程、地形起伏度、坡度、坡形、地层岩性、地质构造及水系因子所占权重分别为0.031 2,0.049 3,0.130 9,0.208 1,0.080 5,0.071 4,0.428 6。
(2) 对茂县斜坡地质灾害易发性评价及区划表明,高易发性区占地面积约46.1 km2,占研究区总占地面积的10.02%,主要分布于研究区的岷江干流沿岸及其部分支流沿岸等;中易发区面积约149.59 km2,占研究区总占地面积的32.52%;低易发区面积约205.25 km2,占研究区总面积的44.62%;非易发区面积约59.06 km2,占研究区总面积的12.84%。
(3) 茂县斜坡地质灾害易发性评价及区划成果与野外调查的地质灾害隐患点分布基本切合,证明基于层次分析法的地质灾害易发性评价结果是有效合理的,可为茂县斜坡地质灾害防治及土体规划利用提供依据。
[1] 柴宗新. 山地灾害概念之我见[J]. 山地学报, 1999, 17(1):91-94.
[2] 孟庆华, 孙炜锋, 王 涛. 陕西凤县地质灾害易发性评价研究[J]. 工程地质学报, 2011, 19(3):388-396.
[3] 王 哲, 易发成. 基于层次分析法的绵阳市地质灾害易发性评价[J]. 自然灾害学报, 2009, 18(1):14-23.
[4] 唐 川, 许 强. 强震区城市地质灾害风险管理的研究内容与方法探讨[J]. 工程地质学报, 2009, 17(1):56-61.
[5] 赵 成, 张永军, 赵玉红. 层次分析法在甘肃省地质灾害易发性评价中的应用[J]. 冰川冻土, 2009, 31(1):186-192.
[6]CASCINI L, BONNARD C. Landslide Hazard and Risk Zoning for Urban Planning and Development[J]. Landslide Risk Management, 2005,(7):199-235.
[7] CARRARA A, GUZZETTI F. Use of GIS Technology in the Prediction and Monitoring of Landslide Hazard[J] . Natural Hazards, 1999,20(2):117-135.
[8] 唐 川, 朱 静. 澜沧江中下游滑坡泥石流分布规律与危险区划[J]. 地理学报, 1999,54(6):84-92.
[9] 金艳珠, 谈树成, 虎雄岗,等. 基于层次分析法与GIS相结合的岩溶塌陷地质灾害易发性分区评估——以云南省师宗县为例[J]. 热带地理, 2012, 32(2):173-178.
[10]谷天峰, 王家鼎. 地理信息系统在黄土工程地质中的应用[M].北京:地震出版社, 2013.
[11]铁永波, 唐 川. 层次分析法在单沟泥石流危险度评价中的应用[J]. 中国地质灾害与防治学报, 2006, 17(4):79-84.
(编辑:刘运飞)
AHP-based Evaluation of Slope Geo-hazard Susceptibility ofMaoxian County, Sichuan, China
LIU Yu-heng, DENG Hui, XIONG Qian-ying
(State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,Chengdu University of Technology,Chengdu 610059,China)
Maoxian county is located in the deep valley region of southwest China with severe slope geological hazards, hence is a good experimental base for characteristic research and susceptibility evaluation of geological disasters. In this research, Analytical Hierarchy Process (AHP) was adopted for the evaluation and zoning of geological disaster susceptibility in the study area based on geo-hazard investigation and remote sensing data interpretation. Seven indices inclusive of height, land relieve, slope shape, gradient, lithology, water, and geological structure were selected as evaluation indicators. Result show that the area of high susceptibility covers 46.1 km2, accounting for 10.02% and distributing mainly along mainstream Minjiang River and some tributaries; the area of medium susceptibility covers 149.59 km2, accounting for 32.52%; and area of low susceptibility is 205.25 km2, taking up 44.62%; and the stable area covers 59.06 km2, comprising 12. 84%.The results are consistent with field investigation results in general, and thus could be taken as basis for land use planning and slope geo-hazard prevention and reduction in Maoxian county.
slope geo-hazard; susceptibility evaluation; Maoxian county; GIS; AHP
2016-02-26;
2016-04-05
中国地质调查局项目(12120113010500)
刘宇恒(1991-),男,四川眉山人,硕士研究生,从事岩土工程及地质灾害方面的研究,(电话)18121960708(电子信箱)348196128@qq.com。
10.11988/ckyyb.20160155
2017,34(5):31-35
P694
A
1001-5485(2017)05-0031-05
