基于Hopfield神经网络的打磨工艺路线优化
2017-05-18崔光鲁陈劲杰徐希羊
崔光鲁,陈劲杰,徐希羊,周 媛
(上海理工大学 机械工程学院,上海 200093)
基于Hopfield神经网络的打磨工艺路线优化
崔光鲁,陈劲杰,徐希羊,周 媛
(上海理工大学 机械工程学院,上海 200093)
为提升工件表面处理工艺品质,提出运用人工智能的方法解决打磨工艺执行路线决策问题。基于人工神经网络思想,利用连续型Hopfield神经网络算法,对打磨工艺执行路线进行优化排序。文中以锅具打磨为分析案例,展示具体应用方法。得出了更加优化的锅具表面打磨工艺执行路线,为以后工件表面处理更加智能高效提供了理论依据。
决策优化;智能算法;Hopfield神经网络;工艺排序方法
随着现代工业产品复杂程度的不断增加,新的加工制造方法也层出不穷,导致了产品的生产工艺路线的可行解也成指数方式增长。为了与新的发展形势相适应,人工智能算法可为工艺路线提供一种更加智能且行之有效的解决方法。
1 传统工艺决策分析
传统的工艺决策路线是分级、分阶段地考虑几何特征、加工工艺要求、工艺实现方法与优化指标等约束条件的,最后得出各工序较为合理的安排顺序。存在着工艺决策智能化水平较低、过程与设计经验难以提取等缺点。当产品工艺路线网络图中可能的组合方案较多时,枚举法不再适用[1],就需要寻求一些智能算法对生产中最优的工艺执行路线进行求解。
2 智能工艺路线
打磨生产过程中,需要综合考虑制造资源、生产实效两方面的因素。制造资源包括打磨所使用的执行设备、打磨材料、夹具等,生产实效则为打磨效果、实现成本、加工效率等。上述两方面因素构成了对打磨的限制约束,以成本低、效率高为优化目标。打磨过程的排序问题就转化为寻找制造资源的变换次数最少的执行路线问题[2]。
2.1 Hopfield神经网络概述
Hopfield神经网络是一种互联型的网络,它引入类似于Lyapunov能量函数概念,将所求问题转换为系统稳定性问题。系统的稳定性可用“能量函数”进行分析[3]。将系统状态稳定点看作能量函数的极小点,将能量函数看作需要优化问题的目标函数,则网络系统从初始状态向稳定点演化的过程就是问题最优解的求解过程[4-5]。
离散型Hopfield神经网络(DHNN)当中,每一神经元输出只可为二值状态(0或1),其激活函数一般用阙值函数来表示[6]。连续型Hopfield神经网络(CHNN)利用Sigmoid函数替代阙值函数作为神经元的激活函数[7]。
CHNN能量函数可表示为如下形式
(1)
f-1是神经元转移函数的反函数[8]。伴随着网络状态的演变能量降低。当网络中所有的神经元节点状态不再发生变化时,网络能量保持在某一稳定值[9],该能量值就是网络的稳定状态。
2.2 求解打磨工艺路线
利用连续型Hopfield神经网络求解工艺路线最优化问题的一般步骤[10]:
(1)将待优化问题映射到连续型Hopfield网络上,并由换位矩阵来表示此映射问题;
(2)将待优化问题对应的目标函数转换成二次型能量函数
(2)
(3)确定网络对应的动态方程,连续型Hopfield神经网络为梯度系统,有如下条件
(3)
vi=Ø(ui)(i=1,2,…,n)
(4)
ki>0,通常取ki=1,Ø用双曲正切函数表示,即
v1=[1+tanh(ui/u0)]/2
(5)
(4)选择合适的初值,将u1(0),u2(0),…,un(0)带入进行迭代计算,使网络按照动态方程进行演化直至收敛,对应的输出即为最佳的排序解[11-12]。
3 应用实例
现在以圆形带双耳平底锅为例,进行表面分区并利用连续型Hopfield神经网络对其打磨工艺路线决策进行研究。
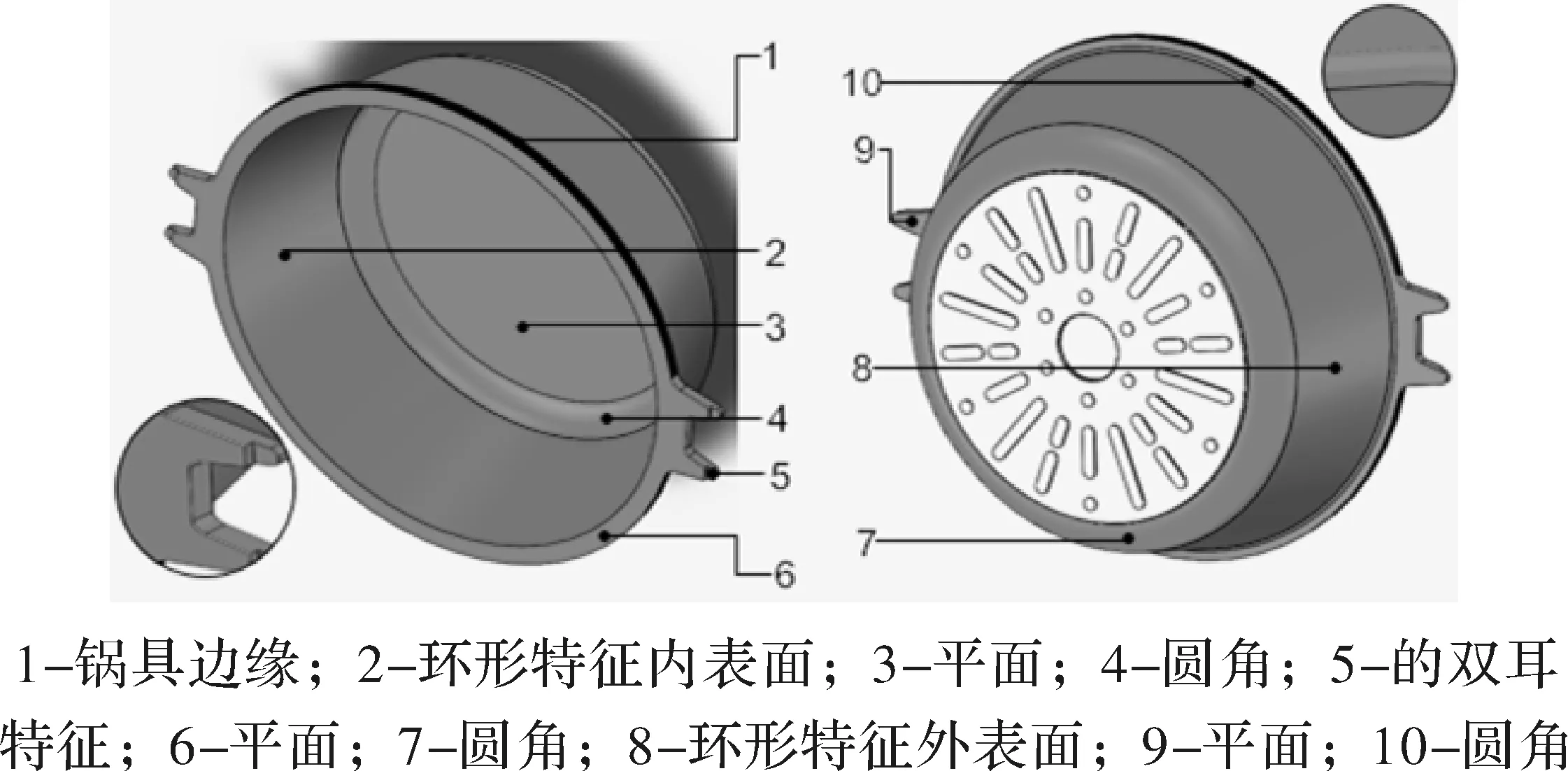
图1 待打磨锅具特征表面分区
3.1 提取模型并集合工艺路线
工艺路线决策即为带约束条件的排序问题,对应的约束就是排序相关工艺流程。将工艺信息按照自定义规则转化为数字信息。转化后的特征量化值代入到工艺排序的能量函数当中,就可以求解出在一定约束条件下的决策排序问题[13]。
待打磨锅具表面的特征量化公式[13]为
x=7a+5b+3c
(6)
式中,x为待打磨锅具表面的特征量化值;a为待打磨锅具表面的特征类型;b为待打磨锅具表面的尺寸面积;c待打磨锅具表面的缺陷类型。
确定变量a、b、c的取值,对应有飞边的特征表面令c=0.05,对应有毛刺的特征表面令c=0.01。根据上述赋值原则可得待打磨特征面a、b、c、x的取值,如表1所示。

表1 锅具待打磨面的特征量化值
3.2 Hopfield神经网络的引入
将锅具表面打磨工艺路线决策问题映射到一个连续型Hopfield神经网络上,每个神经元的输出都用0与1表示,用换位矩阵的形式来表示[14]。
排序决策能量函数如下
(7)
式中,能量E1表示位置行约束,A是>0的常数,当E1=0时每个打磨活动只在打磨路线中出现一次
(8)
式中,能量E2为位置列约束;B是>0的常数,当E2=0时每个打磨活动只在打磨路线中出现一次
(9)
式中,能量E3表示换位矩阵全局约束;C是>0的常数,当E3=0时所有打磨活动的总和为n;A、B、C是约束值,都>0,算法执行前规定好取值的常数。
打磨活动约束关系量化为Δxi=|xi-xi+1|>0,xi为各个表面的特征量化值。Δxi的值越小,表示打磨活动x排在y之前的可能性越大,约束公式如下
(10)
式中,D为约束常量是>0的常数。连续型Hopfield网络排序决策的能量函数如下
E=E1+E2+E3+E4
(11)
式中,E1、E2、E3是惩罚项;E4是目标项。当n个待打磨表面排序决策完成之后,相邻两面对应的特征量化值差值Δxi的和即是最小值[15]。
打磨工艺决策问题的网络状态方程与输出方程,具体形式如下
(12)
vxi=Ø(uxi)=[1+tanh(uxi/u0)]/2
(13)
式(12)中τ是常数,一般取值为1,换位矩阵可表示为T=|vij|T,打磨工序排序决策前后各序号之间关系为
Y=XT
(14)
式中,X为初始打磨序列;Y为经过神经网络排序决策之后的打磨工序。按照特征分区编号顺序设定初始加工序列为
X=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10]
选取适合的初始状态矩阵,初始状态矩阵的选取对神经网络输出的结果有较大影响,一般是在0附近随机产生,在这里选择由0与0.01组成的初始状态矩阵来执行迭代运算[13]。
选取的初始状态矩阵
将待打磨锅具表面特征量化值与初始状态矩阵输入神经网络的状态方程与输出方程当中,借助Matlab软件编程实现[16]。设置网络参数为A=200,B=200,C=50,D=100,设步长Δt=0.000 1,u0=0.1,τ=1,n=10。
当运算迭代执行2 000次之后得到换位矩阵输T,同时得到输出网络能量函数变化曲线如图2所示。
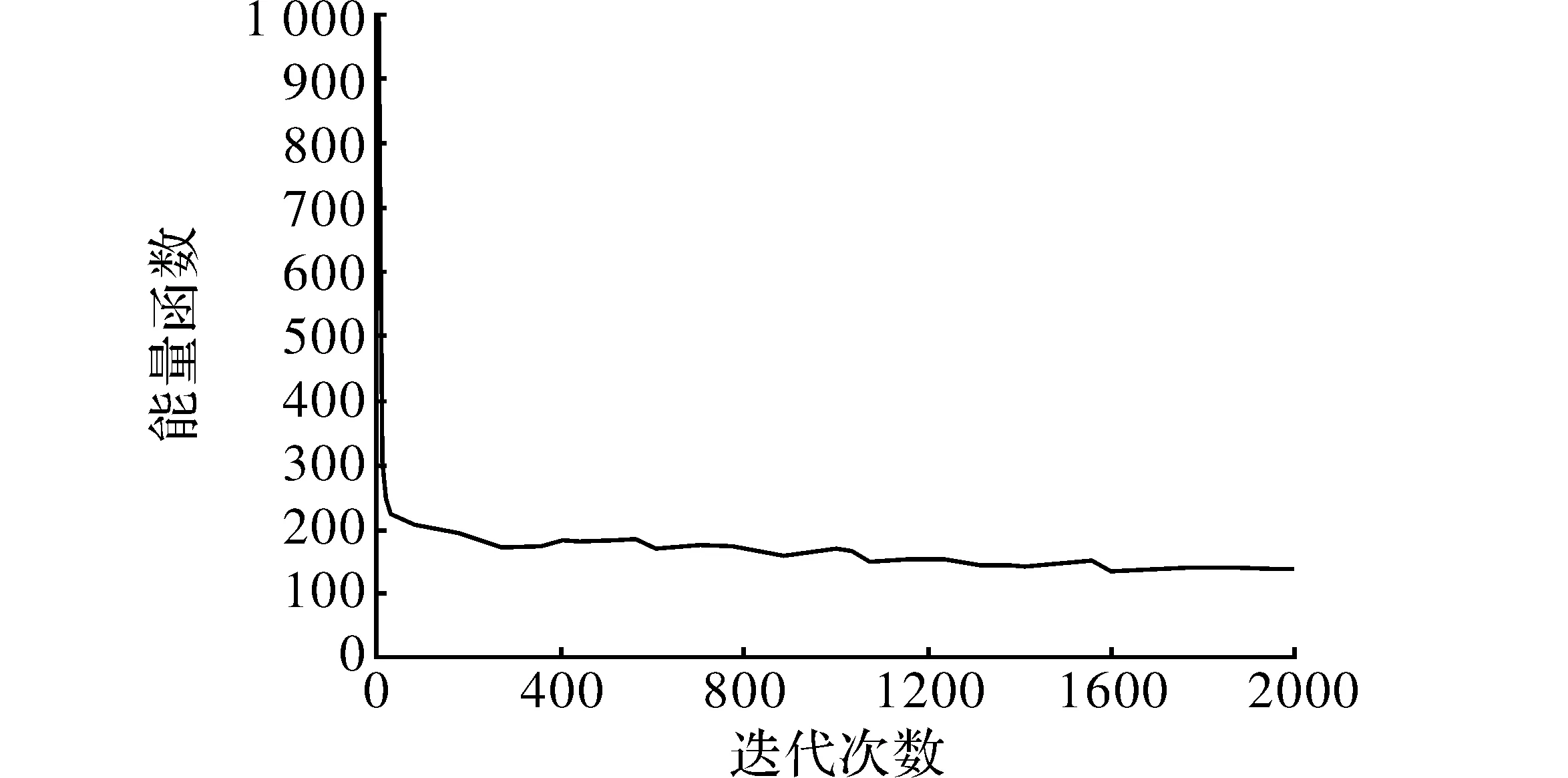
图2 网络能量函数变化曲线
由图2分析可知,网络前期的能量下降较快,在约200次迭代后系统能量呈现缓慢下降的状态,此时也代表网络系统在逐渐逼近系统的排序最优解[17]。Hopfield神经网络在经过2 000次迭代后系统逐渐达到最小能量状态,此时的网络能量即对应着打磨工艺执行路线的排序最优解。
3.3 决策结果

将上式矩阵带入Y=XT可得排序后的打磨工艺路线为
得到锅具外表面打磨路线的先后顺序编号为1-5-6-2-1-3-7-8-10-9,连续型Hopfield神经网络排序算法产生的打磨排序,与实际生产中经过不断实践、反复验证,最终采取的生产流程相一致。表明该算法得出的结果较为理想,可大幅提升打磨工艺排序决策制定的质量。
4 结束语
本文根据人工神经网络的特点与优势,并结合压铸锅具表面打磨的执行特点,运用连续型Hopfield神经网络对各表面的打磨次序进行了决策排序,打磨工艺路线的智能决策实现可以提高机器人打磨效率,但由于在锅具打磨领域的特征量化还没有系统的理论研究,可参照的经验参数还很少,现阶段运用连续型Hopfield神经网络算法所得出的工艺路线还不能达到人工专家决策的效果,但随着理论参数的逐步完善,以神经网络强大的运算能力一定能够得出更加理想的决策效果。
[1] 郎志,李成群,费超.机器人柔性抛光系统研究[J].机械工程师,2006(6):26-28.
[2] Berenji H R,Khoshnevis B.Use of artificial intelligent in automated process planning[J]. Computers in Mechanical Engineering,1986(5):47-55.
[3] Zhang G W, Zhang S C,Xu Y S.Research on flexible transfer line schematic design using hierarchical process planning[J].Journal of Materials Processing Technology,2002,129(2):629-623.
[4] Bonomi E, Lutton J L.The N-city traveling salesman problem: statistical mechanics and metropolis algorithm[J].SIAM Review,1984,26(4):551-569.
[5] Lonel B.Integrating computer aided design and computer aided process planning: a computational techniques model approach[J].Transactions on Information Science and Applications,2008,5(5):786-795.
[6] 徐丽娜.神经网络控制[M].哈尔滨:哈尔滨工业大学出版社,1999.
[7] 陈文宇,吴跃.Hopfield神经网络参数设置[J].计算机工程与应用,2006(31):34-36.
[8] Hopfield J,Tank D W.Neural computation of decisions in optimization problems[J].Biological Cybernetics,1995,23(1):73-78.
[9] 韩力群.人工神经网络理论、设计及应用[M].北京:化学工业出版社,2007.
[10] 姜菀西,李晓东.基于连续型Hopfield人工神经网络的CAPP系统中工序内各表面加工顺序的排序[J].机械制造,2005,43(8):20-22.
[11] Lin A C,Lin S Y, Diganta D.An Integrated approach to determination the sequencing of machining operations for prismatic parts with interacting features [J]. Journal of Material Process Technology, 1998(73):234-250.
[12] Protzel P W,Arras M K.Performance and fault-tolerance of neural networks for optimization [J].IEEE Transactions on Neural Networks,1993,4(4):600-614.
[13] 王桂莲,郭晓云.复杂模具自由曲面抛光工艺规划的研究[J].佳木斯大学学报:自然科学版,2013,10(2):28-36.
[14] 张永弟,李冬才,朱金达.基于Web和数据库的CAPP系统的设计与实施[J].现代管理技术,2008(7):67-68.
[15] 兰兆青. Hopfield神经网络在TSP问题中的应用[D].太原:中北大学,2008.
[16] 徐迪.CAPP中智能工艺决策研究[D].杭州:浙江理工大学,2014.
[17] 孙卫琴.Tomcat与Java Web开发技术详解[M]. 2版.北京:电子工业出版社,2009.
欢迎订阅《电子科技》
邮发代号:52-246
A Grinding Process Route Optimization Based on Hopfield Neural Networks
CUI Guanglu,CHEN Jinjie,XU Xiyang,ZHOU Yuan
(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)
In order to improve the industrial grinding efficiency, we put forward the method of applying artificial intelligence for process execution routes decision. Based on artificial neural network, the continuous Hopfield neural network sorting algorithm is adopted to make process decisions, finding the polishing process execution path by Matlab. It provides theoretical reference for more intelligent and efficient industrial grinding of the future.
decision making optimization; intelligent algorithm; Hopfield neural network; process configuration
2016- 06- 12
上海市自然科学基金(13ZR1458500)
崔光鲁(1990- ),男,硕士研究生。研究方向:智能机器人。陈劲杰(1969- ),男,副教授,硕士生导师。研究方向:智能机器人等。徐希羊(1989- ),男,硕士研究生。研究方向:智能机器人。周媛(1982- ),女,博士,讲师。研究方向:微纳机电系统。
10.16180/j.cnki.issn1007-7820.2017.05.010
TP18
A
1007-7820(2017)05-036-04
