谈电磁学中的“场”和“路”

段杉杉

(东莞市第六高级中学 广东 东莞 523420)

谈电磁学中的“场”和“路”

段杉杉

(东莞市第六高级中学 广东 东莞 523420)

“场”和“路”是电磁学中的两个基本内容，它们在物理内容上有着内在的联系，而在研究方法上又有所区别．由此简要回顾对电磁场和电路问题的基本认识；给出电磁场物理量与电路物理量的对应关系；从电荷守恒和电磁场方程出发，推导出直交流电路均适用的基尔霍夫第一、第二方程式，指出直流电路的基尔霍夫方程式只是其中的特例．

电磁场 电路 基尔霍夫方程 似稳条件

1 电磁场和电路概述

电磁场是物质存在的一种形式，“场”这种物质与实物一样具有能量、质量和动量，它的传播具有一定的速度．在研究场的物理性质时，由于场是空间的点函数，故我们关心的是场中各点的物理过程以及电磁能量在空间的分布，描写电磁场的基本物理量便相应地成为空间矢量点函数．

在电场中，用一个矢量点函数E

(1)

来描写电场在该点的性质，称为电场强度．

在磁场中用磁感应强度B的大小

(2)

来反映该点磁场的强弱，B的方向恰好使运动的正点电荷在该点的受力F与矢量(v×B)同方向．

为了便于描述有介质时的电磁场，引入电位移矢量D和磁场矢量H，定义式为

D=ε0E+P

(3)

(4)

其中P为极化强度，M为磁化强度．E和B为描述电磁场的基本物理量，D和H为相应的辅助物理量．

1819年以前，人们没有认识到电现象与磁现象的相互联系．随着电磁学的发展，人们逐渐发现了变化的电场与变化的磁场间的联系．麦克斯韦在前人实践和认识的基础上对电磁现象做了系统研究和总结，创建了宏观电磁场理论，得出麦克斯韦电磁场方程组．

在电路问题中，是用电路模型和电路的物理量来描述一个系统的电磁过程的，这些物理量有电流i，电压u，电荷量q，磁通ψ等．常见的电路模型由电阻、电感、电容等无源元件和电压源、电流源等有源元件联结而成．对于一定的电路结构和电路参数求出电路中各物理量，则物理系统中的能量变化与转换、信号的传输与再现等状况都会得到解决．故运用电路方程是解决电路问题的基本方法．

根据电磁场的观点，电路中能量的储藏、损耗与转换是通过电磁场在空间各点进行的，故，可以说电磁场的研究方法是比较一般地对物理过程进行全面描述的方法，而电路的研究方法则有其局限性．将二者比较可以看出，场的特点在于逐点地考察电磁场系统中所发生的物理过程，而在电路中，其参数概括了一部分介质的电磁特性，表征电路性质的物理量是一个区域中场量表现的总和．例如，电流强度是一块面积上电流密度的面积分；电压是一段路径上电场强度的线积分，等等．说明场量描述的是一般情况，而“路”的问题是“场”的一种特殊情形．

2 电磁场物理量与电路物理量的关系

前面谈到，在物理内容上，电磁场与电路间有着内在的联系，而在研究电磁过程的方法上则有所不同．电磁场物理量描述场的一般过程，而电路物理量描述电路中场的特殊形式，体现着场量表现的总和．在一定意义上说，场和路是一般与特殊的关系，微分量与积分量的关系．下面表1中，给出场的概念常用物理量和路的概念常用物理量之间的对应关系．

表1 路量与场量的对应关系

从表1可以看出：

(1)电路的物理量都可用场的物理量的空间坐标积分来表示．反之，场的物理量也可以用电路物理量的空间坐标的微商来表示，即“路”量是积分量，“场”量是微分量．前者与较大的空间尺度相关；后者则描述空间各场点的电磁性质．

(2)电路(以及磁路)的物理量既然可由场量来定义，那么，电路(以及磁路)的规律也一定可以由电磁场的规律推导出来．

3 从场方程到路方程

3.1 基尔霍夫第一方程式

图1所示的一般电路中，包含变化电源e及电阻R，电感L，电容C各纯元件．

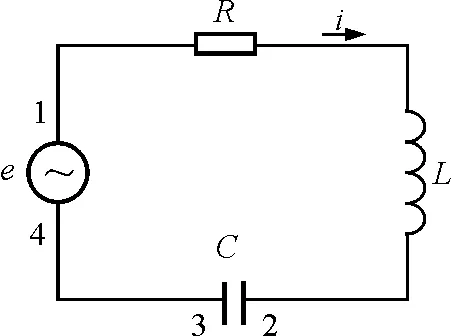
图1 一般电路图

作一闭合曲面A′包围节点1，非稳恒情况下，对A′曲面，由电荷守恒定律

(5)

式中j为A′面内导线上的传导电流密度(非高频场中，可略去导线中的位移电流)，dA′为A′面上的面元，上式左边的积分等于流出节点1的传导电流之和，即

∮A′j·dA′=∑im

(6)

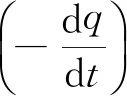
(7)

式(5)可写为

∑im=-∑id

(8)

令

∑i=∑im+∑id

(9)

得到

∑i=0

(10)

式(10)称为基尔霍夫第一方程式(第一定律)，又称为节电电流方程．∑i是节点1处流出的传导电流与流出的位移电流的总代数和，即全电流．式(10)表明，在电路(直流或交流)的任一节点处，传导电流和位移电流的总代数和为零，或说全电流的代数和为零．

以图1所示电路为例，从A′面或节点1处流出的传导电流代数和为

∑im=ie+iR+iL+iC

此式右侧各项分别是通过电源、电阻、电感、电容各支路的瞬时电流．令流出节点的电流流向为正，id为节点1处流过分布电容的瞬时位移电流，于是式(10)的具体形式为

∑i=ie+iR+iL+iC+id=0

在频率很低或直流电情形，id可忽略或为零．

以上运用电荷守恒定律，在非稳恒电路的一般情况下，推导出直流电路的基尔霍夫第一方程式．对于直流电路的特殊情况，因为电路中没有电感、电容元件，且无位移电流．故基尔霍夫第一方程式(10)的形式更为简单．在电磁学中，导直流电路的基尔霍夫第一方程式时，是从电荷守恒定律的特殊形式，即电流的稳恒条件

∮A′j·dA′=0

(11)

出发，而导出在电路任一节点处直流电流强度的代数和为零，即

∑I=0

(12)

显然，它只是(10)式的特例．

3.2 基尔霍夫第二方程式

图2所示为一个任意闭合电路，包含有电源e，电阻R，电感L和电容C．在电磁学中，对直流电路基尔霍夫第二方程式(第二定律)是从稳恒电场的场强环路定理∮lE·dl=0出发而推导出来的．这里对闭合回路l，运用麦克斯韦方程组中的电场环流方程，即

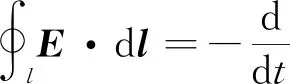
(13)

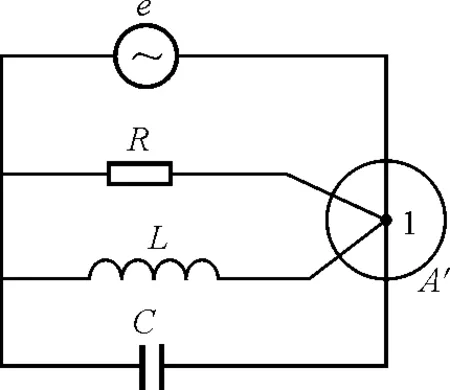
图2 任意闭合电路图

式中l为闭合电路的几何路径，A为l所围得面积，B是包括l在内的回路面积处的磁感应强度．

在有非静电力的区域，欧姆定律的微分形式为

j=σ(E+E非)

(14)

电源内部的电场强度

(15)

对电源外部的导线和电阻中，电场强度为

(16)

由式(13)左边

(17)

上式右端第一项是闭合电路中除电容器两极之间以外其他各段上的电势降落，第二项是电容器两端的电势降落，第三项为电源的电动势，即

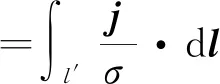
(18)

(19)

(20)

式中l′为回路l中除电容两极板间之外其他各段路径．则式(17)变为

∮lE·dl=iR总+uc-ε0

(21)

对式(13)右边，按磁感应强度B及磁通变化率的含义，其应等于回路上自感电动势与互感电动势的代数和，即

(22)

其中L′是除电路内的电感L外的寄生电感．因为电路构成的回路包围一定的面积，并在其中产生磁通，故总会产生一定的寄生电感．用LΣ=L+L′表示该回电路的总电感，用∑ε=ε0+εM表示回路的总电动势，即电源电动势加互感电动势(这里未包括自感电动势，它将以电势降落的形式在下面式子中出现)．综合式(13)、(21)、(22)得

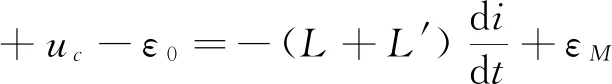
即

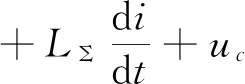
(23)

该式表明，任意一个闭合回路中，电动势的代数和等于电阻、电感、电容上电势降落的代数和．用∑u表示回路的电势降落代数和，式(23)可写成更一般的形式，即

∑ε=∑u

(24)

这就是直流电路的基尔霍夫第二方程(第二定律)，又称回路电压方程．

对于稳恒(直流)电路，B和i不随时间变化，且没有电容C，于是式(23)简化为

ε0=iR总

(25)

∑ε=∑U

(26)

它表明，在任一直流电路中，各电源的电动势代数和等于各电阻上电势降落的代数和，这正是直流电路的基尔霍夫第二方程式，它只是式(24)的特例．

直流电路的基尔霍夫第一、第二方程式，可以分别从电流的稳恒条件和稳恒电场的场强环路定理导出，显然这两个方程式只适用于稳恒电流和稳恒电场的情形．而交流的基尔霍夫方程式的成立条件则要求电路满足似稳条件，即所讨论电路的尺寸远小于电路激发的电磁波的波长，l≪λ．在这个范围内，可以认为电磁场变化足够缓慢，允许忽略电磁波的传播时间，以致在电路的尺寸范围内，认为不存在因传播过程而造成的位相差．例如，不论在电路的任何地方，其交流电流i，交流电压u，交变电动势ε，可以忽略它们之间的位相差，前面基尔霍夫第二方程的式(23)便是在此条件下推导出来的．对于迅变电磁场和高频电路中，显然已不满足似稳条件，上述的基尔霍夫第一、二方程式不再适用．

4 结论

电磁学中的场和路联系十分密切，场的特点在于逐点地考察电磁场系统中所发生的物理过程，而电路的参量是一定区域中场量表现的总和，电路的过程是电磁场在特定边界条件下的表现．描述电磁场的物理量和描述电路的物理量有着微分和积分的关系．运用电荷守恒定律和麦克斯韦方程组中的电场环流方程推导出交直流电的基尔霍夫第一、二方程式，它们将电磁学中直流电的基尔霍夫第一、二方程式作为特例概括于其中．

1 梁灿彬,秦克戎，梁竹键．电磁学．北京：高等教育出版社，1980.234～244，633～636

2 赵凯华,陈熙谋．电磁学(第二版)．北京：高等教育出版社，1985.290～296

3 胡友秋,程福臻．电磁学(第一版)．北京：高等教育出版社，1994.175～185，324～334

4 (美)J·D·克劳斯．电磁学．安绍萱，译．北京：人民邮政出版社，1979.224～225，364～375

5 大学物理编辑部．大学物理(电磁学专辑)．北京：北京工业大学出版社，1988.262～264

6 贾起民,郑永令．电磁学(上册)．上海：复旦大学出版社.1987.317～323

7 冯兹璋．电磁场．北京：人民教育出版社.1980.450～452

8 郭硕鸿．电动力学．北京：高等教育出版社.1979.19～22

9 R.P.Winch.Electricity and Magnetism.Prentice-Hall，Inc，1955.19～23，226～228

Talkingaboutonthe“Field”and“Road”ofElectromagnetism

DuanShanshan

(DongguangNO.6SeniorHighSchool,Dongguan,Guandong523420)

Electromagnetic fields and electric circuits are two basic concepts in electromagnetics. They share an internal connection in physical meaning, while differ in research method. This paper mainly reviews the basic knowledge of electromagnetic fields and electric circuits. Additionally, the corresponding relationship between physical quantities of the two concepts is provided. Based on the conservation of charge and the electromagnetic field, the Kirchhoff first and second equations which can be applied to Direct AC circuit are deducted. The Kirchhoff equation is just an exception in the DC circuit.

electromagnetic fields;electric circuits;kirchhoff equation;quasi steady state

2016-11-23)