不完备序信息系统的集对优势度粗糙集模型①
2017-05-18黄丽萍
黄丽萍
(闽南师范大学计算机学院,福建漳州363000)
不完备序信息系统的集对优势度粗糙集模型①
黄丽萍
(闽南师范大学计算机学院,福建漳州363000)
不完备序信息系统粗糙集模型是经典粗糙集模型的扩展,它能进一步处理含未知属性值和具有优势关系的数据.针对相似优势关系条件过于宽松而限制扩展优势关系条件又过于严格的缺点,引入集对分析思想,提出了集对优势度粗糙集模型.它可以通过调整参数,达到较理想的分类,克服了现有不完备序信息系统优势关系的不足.并以实例分析验证了集对优势度粗糙模型的有效性.最后,在UCI数据集上进行仿真实验,通过实验进一步说明集对优势度粗糙模型可以获得更优的分类效果.
粗糙集,不完备序信息系统,限制优势关系,对优势度
Pawlak[1]提出的经典粗糙集理论是以完备信息系统为研究对象.但现实世界,由于数据理解、获取过程中噪音的影响、获取技术的限制等因素,不完备信息系统广泛地存在现实生活中.而经典粗糙集并不适用于不完备信息系统,这就有必要对它进行扩充以处理不完备数据.许多学者针对不完备信息系统缺失给出不同理解,得出相应的扩展粗糙集模型,如Kryszkiewicz[2]提出基于容差关系的粗糙集模型;Stefanowski等[3]提出了基于非对称相似关系和量化容差关系的粗糙集模型;王国胤[4]提出了基于限制容差关系的粗糙集模型.
在实际问题中,属性的取值不仅含有不完整的数据而且往往数值之间具有优势关系.属性值的有序特性是非常重要的.如决策系统中的效益型和成本型属性则说明了在系统中采用有序思想的重要性,该类问题更能客地描述众多决策问题[5].而粗糙集的等价关系不能处理该类数据,因此,Greco等[6]提出了基于优势关系的粗糙集模型,用优势关系代替了等价关系.对于上述两类问题的处理,Shao[7]提出了基于优势关系的不完备序信息系统的属性约简和规则提取.针对Shao的相似优势关系过于宽松的问题,胡明礼等[8]引入了阀值广义扩展优势关系;骆公志等[9]进一步提出了限制优势粗糙集模型,避免了相似优势关系条件过于宽松的现象,但在某些情况下又显得过于严格.韦碧鹏等[10]提出了α优势下的粗糙集模型的属性约简,莫京兰等[11]提出的不完备序信息系统及其扩展模型,陶志等[12]提出的概率优势关系和施玉杰等[13]提出的α先验概率优势关系下的粗糙集模型,这些模型都需要统计各个属性中各数据值出现的频率;对于大数据来说,计算各数据值出现的频率已经需要花费大量的时间代价,显然不符合实际.
集对分析方法[14]是赵克勤教授近年来提出的用于研究集合之间相互关系的一种新理论,其核心思想是把被研究的客观事物之确定性联系和不确定性联系作为一个系统来处理,现在它已经得到了广泛的应用.一些学者利用运用集对分析方法对不完备信息系统粗糙集模型进行了扩展,建立了相应的不完备信息系统的集对粗糙集模型[15-18].而不完备序信息系统的集对分析方法目前还较少.文献[19]将集对分析方法应用于不完备序信息系统,提出了关键属性,而关键属性的认定具有人为因素,主观性过强.因此,本文在分析现有不完备序信息系统的几种粗糙集模型的基础上,提出了集对优势度粗糙模型.
1 基本概念

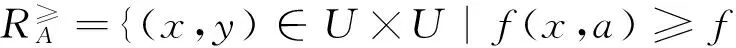
1.1 相似优势关系
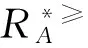
1.2 限制优势关系
定义3[9]设IIS=〈U,AT,V,f〉是一个不完备序信息系统,对于A⊆AT,∀x,y∈U,对象在属性A下的限制优势关系为

限制相似优势关系克服了相似优势关系限制条件过于宽松的不足;但其条件过于苛刻,容易将实际上具有很大可能性的同类对象误判为不同类.如信息表中属性a的值域为[1-8],存在y(a)=*,x(a)=1,按照限制相似优势的定义有y(a)=*优于x(a)=1,但是对于y(a)=*,x(a)=3,则不能判断y(a)=*优于x(a)=3.而实际上,如果y(a)的取值满足均值分布,则y(a)>x(a)的概率很大,因此,y(a)优于x(a)成立的可能性很大,所以限制相似优势关系会造成一定的分类错误.
针对上述存在的问题,本文提出了集对优势度粗糙集模型.
2 集对优势度粗糙集模型

M(x,y)={a∈A|fa(x)≥fa(y)∨(fa(x)=maxva∧fa(y)=*)∨(fa(x)=*∧fa(y)=minva)},
N(x,y)={a∈A|(fa(x)=*∧fa(y)=*)∨(fa(x)≠*∧fa(x)≠maxva∧fa(y)=*)∨
(fa(x)=*∧fa(y)≠minva∧fa(y)≠*)},
K(x,y)={a∈A|(fa(x) 显然0≤S1,S2,S3≤1,S1+S2+S3=1. 对于弱势度中的对象如何定义其中可能的优势度,本文给出对象属性值联合优势率的定义. 定义6 设IIS=〈U,AT,V,f〉是不完备序信息系统,B⊆AT,对于任意的x,y∈U,对象x,y属性值联合优势率FP(x,y)定义为 在差异对象中,对象属性值联合优势率通过用平均值来代替未知值*来进行优劣比较,不仅解决相似优势关系和限制优势关系不能合理地比较f(x,a)=Vi(Vi∈Va∧Vi≠maxVa∧Vi≠minVa),f(y,a)=*的情形;也克服了文献[16]中依靠专家选择一些属性作为关键属性而导致的主观性过强. 证明 由定义7可知,当S1=1时,只考虑强优势度不考虑弱优势度,这时集对优势关系的定义等价于限制优势关系的定义;当S1+S2=1,即不对弱势度进行进一步限定,则集对优势关系的定义等价于相似优势关系的定义.从而可得性质2.从性质2可以看出,本文提出的集对优势度粗糙模型客服了相似优势关系划分粒度过大和限制优势关系划分过小的缺点,对不完备序信息系统的处理更加合理. 文献[20]给出的一个完备的序信息系统,有11个对象U={x1,x2,…,x11},8个条件属性AT={a1,a2,…,a8}.条件属性值A>B>C>D,分别用4,3,2,1来表示.将表内一些对象设置成未知值,用*表示;从而得到一个不完备序信息系统如表1所示.运用表1给出的不完备序信息系统来分析文献[6]提出的相似优势关系、文献[9]提出的限制优势关系以及本文提出的优势关系之间的分类效果. 表1 不完备序信息系统 从上面的结果可以看出,集对优势度优势关系通过平均值来代替未知值来进行比较的方法,解决了相似优势关系条件过于宽松而限制优势关系条件过于苛刻的问题,使基于集对优势度的优势关系的优势类更接近信息完备时的优势类,具有更优的分类效果. 下面通过MATLAB,选用表1和UCI数据库中的IRIS数据集,进一步验证基于集对优势度的优势关系的分类性能.采用随机函数分别对表1和IRIS数据集设置5%,10%,20%和40%数据量的未知值,然后用集对优势度优势关系、限制相似优势关系对对象进行划分,产生各对象的优势类,将各对象的优势类与其相应的未设未知值时的优势类(标准类),利用文献[21]所给分类误判率公式计算两者之间的误分类率. 表2 分类错误率比较 实验结果表明,限制相似优势关系的分类误判率明显高于本文基于集对优势度的优势关系;且随着信息不完备率的增加,其误判率快速上升,而基于集对优势度的优势关系的误判率比较稳定.通过调节α的大小,可以进一步提高分类精度.当α=0.6是的分类误判率小于α=1时的分类误判率.可以进一步看出,对于序信息系统的分类,若分类条件过于苛刻,容易将实际上具有很大可能性的同类对象误判为不同类. 现实中,存在很多不完备且含有序关系的数据,因此对这种复杂数据的处理是很有意义的.本文通过对不完备信息系统和优势关系的分析,结合集对分析方法提出了集对优势度粗糙模型.该方法对于不完备序信息系统的数据分析更加合理.这种模型可根据实际应用的需求,对参数α合理地调节,可以灵活地控制从不完备序信息系统中获取信息粒度的大小;从而更有效地对数据进行处理,克服了已有扩展模型的局限性.在本文的基础上,下一步将进一步研究基于集对优势度的不完备序决策系统的属性约简和规则提取方法. [1]PawlakZ.Roughset[J].InternationalJournalofComputerandInformationSciences,1982,11:341-356. [2]KryszkiewiczM.Roughsetapproachtoincompleteinformationsystem[J].InformationSciences,1998,112:39-49. [3]StefanowskiJ,TsoukiasA.OntheExtensionofRoughSetsUnderIncompleteInformation[C].//ProceedingsofNewDirectionsinRoughSets,DataMiningandGranular-SoftComputing.Berlin:Springer,1999:73-81. [4] 王国胤.Rough集理论在不完备信息系统中的扩充[J].计算机研究与发展,2002,39(10):1 238-1 243. [5] 黄丽萍.区间序信息系统在向量相似度下的优势关系及属性约简[J].齐齐哈尔大学学报:自然科学版,2015,31(6):1-4. [6]GrecoS,MatarazzoB.SlowingskiR.Roughsetstheoryformulticriteriadecisionanalysis[J].EuropeanJournalofOperationalResearch,2001,129(1):1-47. [7]ShaoMW,ZhangWX.Dominancerelationandrulesinanincompleteorderedinformationsystem[J],InternationalJournalofIntelligentSystems,2005,20:13-27. [8] 胡明礼,刘思峰.基于广义扩展优势关系的粗糙决策分析方法[J].控制与决策,2007,22(12):1 347-1 351. [9] 骆公志,杨晓江,周德群.基于限制扩展优势关系的粗糙决策分析模型[J].系统管理学报,2009,18(4):391-396. [10] 韦碧鹏,吕跃进,李金海.α优势下的粗糙集模型的属性约简[J].智能系统学报,2014,9(2):251-257. [11] 陶志,胡树芹,不完备偏好决策系统中一种扩展优势关系模型.中国民航大学学报,2015,32(4):51-55. [12] 施玉杰,杨宏志,徐久成.α先验概率优势关系下的粗糙集模型研究[J].南京大学学报:自然科学版,2016,52(5):899-907. [13] 莫京兰,吕跃进,李金海.不完备序信息系统的模型扩展及其属性约简[J].南京大学学报:自然科学版,2015,51(2):430-437. [14] 赵克勤.集对分析及其初步应用[M].1版.杭州:浙江科学技术出版社,2000. [15] 黄兵,周献中.基于集对分析的不完备信息系统粗糙集模型[J].计算机科学,2002,29(7):1-3. [16] 刘富春.变集对联系度的扩充粗糙集模型及其属性约简[J].计算机科学,2006,33(3):185-187. [17] 李长清,李克典,李进金.不完备信息系统确定性和集对联系度的粗糙扩展模型[J].工程数学学报,2010,27(2):342-346. [18] 赵焕焕,菅利荣,刘勇.基于顺势相似关系的变精度粗糙集模型[J].计算机工程与应用,2017,53(6):51-56. [19] 翟育明,蔡红,郭斌.(α,β)集对限制优势粗糙集及决策模型[J].系统管理学报,2014,23(3):437-443. [20] 菅利荣,刘思峰,谢乃明.杂合灰色聚类与扩展优势粗集的概率决策方法[J].系统工程学报,2010,25(4):554-560. [21]WinterS.Locationsimilarityofregions[J].ISPRSJournalofPhotogrammetry&RemoteSensing(S0924-2716),2000,55:189-200 Incomplete Ordered Information System Rough Set Model Based on Set-Pair Dominant Degree HUANG Li-ping (School of Computer,Minnan Normal University,Zhangzhou 363000,China) Rough set model of incomplete ordered information system is an extension of classical rough set model,which can deal with the data with unknown attribute values and dominance relation.For similar dominance relation condition was too loose and limited extended dominance relation was too strict,motivated by the problem,set-pair dominant degree rough set model was proposed base on the analysis of set-pair,which can be by adjusting the parameters,to achieve the ideal classification,overcome the shortcomings of the dominance relation in the existing incomplete ordered information system definition.And the feasibility of the model was verified by an example.Finally,we carried on the simulation experiment on UCI data sets and the experimental results illustrate that the classification results were more accuracy can be obtained based on the set pair dominance relation. rough set,incomplete ordered information system,limited dominant relation,set-pair dominant degree 2016-12-13 福建省教育厅科技项目(JAT160305)资助 黄丽萍,E-mail:liphuang@126.com. TP391 A 1672-6634(2017)01-0097-05
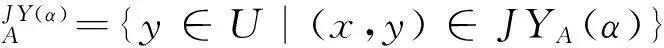


3 实例分析
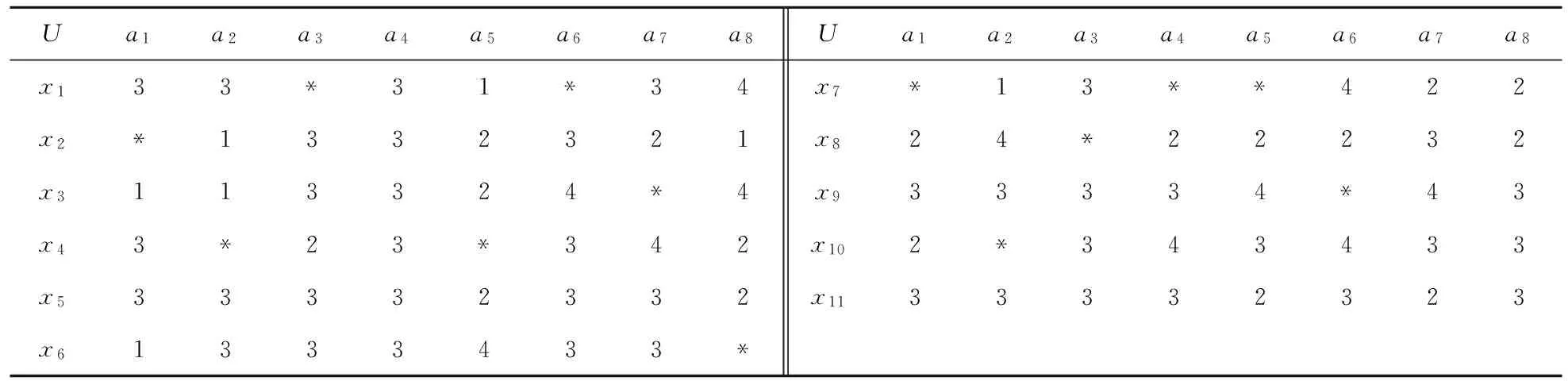

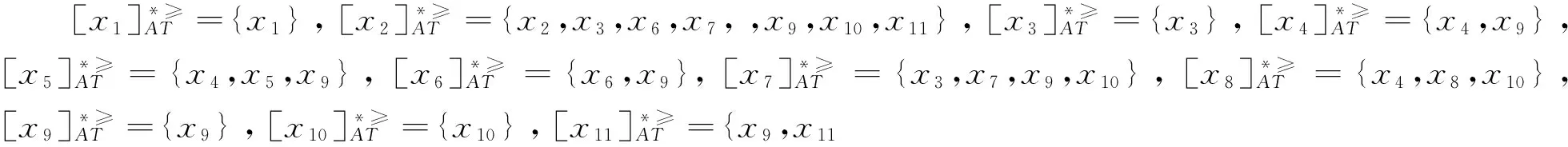

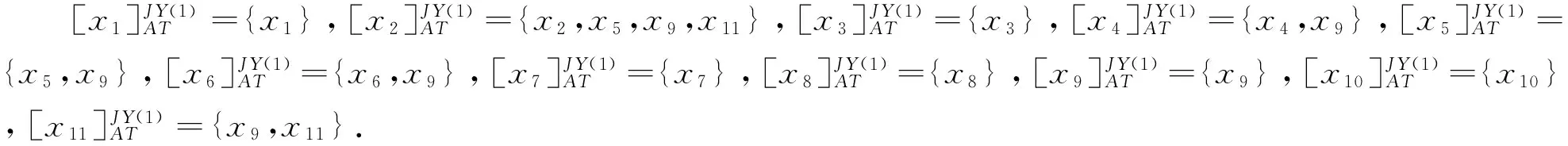
4 仿真实验


5 结束语
