利用“数学工具”探索数学问题解决教学模式初探

罗海霞

摘要：问题解决是数学课程培养的核心素养之一。从中职生的数学学习特点出发，充分挖掘数学工具辅助学生解决数学问题的作用，探索问题解决教学模式的主要特征、教学程序及评价方法等。

关键词：教学模式；问题解决；数学工具

中图分类号：G712 文献标志码：A 文章编号：1673-9094-（2017）02/03C-0018-04

“数学工具”指数学教学过程中，为更好地促进并达成学习目标所采用的工具，主要指数学软件或数学辞典等。本课题指几何画板、计算器、EXCEI等较为普及的数学教学软件。这些教学软件具有强大的计算、作图、列表、动画、演示等功能。“在讲抽象的概念之前，运用计算机和数学软件的计算、演示、模拟功能，让学生自己去分析、发现其中的规律，在真正讲授抽象概念时，就不会感到突然。在讲述定理时，也可以参照这个办法。在计算机的帮助下，可以将以往繁重的、手工不能实现的计算变得轻松起来……这样就可以将实际问题引进课堂，让学生体会数学的实际价值”。研究证明，数学工具可以弥补学生抽象思维能力的不足，让他们在动手实践的过程中理解知识、应用知识，从而促进他们利用数学工具进行计算、思维和应用的能力。据此，笔者尝试在中等职业学校开展利用数学工具的教学，并根据中职生的认知特点和教学规律，构建起问题解决教学模式。

一、数学工具辅助学生问题解决学习的可能性

问题解决教学的教育价值在于培养学生学会观察、分类、概括、归纳、一般化、特殊化、分析解决问题的思维能力，运用原有的知识和经验解决新的陌生的问题。《中等职业学校数学课程标准》明确指出：“培养学生运用计算器、计算机进行计算的能力……学会分析问题、解决问题的问题解决的能力”。新的课标要求充分明确数学工具的功能与价值。我们不能再简单满足于用几何画板研制个别课例，或将计算器、EXCEL的部分操作案例仅仅作为教材的附录加以介绍，而需要利用数学工具引导中职生开展问题解决教学，并逐步构建有效的教学模式。

中职生大部分是怕学数学的，具体表现在“认知障碍、记忆障碍、阅读障碍、运算障碍”等方面的困难，一部分学生“多动、分心、固执、笨拙、冲动、孤僻”的行为特征也不利于学好数学。心理学家沃纳认为“处于这种状态的学生，往往在数学学习方面表现出审题能力差，抽象思维能力薄弱，空间认知能力低，记忆力低，导致的运算障碍等”。针对这样的学生“在学力补救中，将教学方式结构化（从个别教学到小组教学），使学生大量体验自我表达及和别人进行问答的习惯”。

问题解决学习具有在教学方式结构化的情境中开展学习的特点。问题解决学习起源于20世纪50年代美国的医学教育。它的原型基本特征有五个方面：（1）将学生分组；（2）组内对问题进行研究和讨论学习；（3）学生进行自我指导；（4）再次集合汇报各自学习心得，并处理问题；（5）学生对自己的工作进行自评和组评。通过问题解决对数学知识形成深刻的、结构化的理解，形成问题解决的技能，发展自主学习能力。问题解决是贯穿学习始终的核心，主要特征包括目的指向性；心理过程的一系列操作序列为了达到某种终结状态，而采用的认知操作过程。

同时，我们也应该警惕问题教学在实践中的不足，“忽略操作的作用而总是保持在语言水平上，特别在数学教育中这是一个严重的错误……操作和数学实验远非阻碍了演绎思想的后期发展，事实上它组成了一个必要的准备”[5]。因此使用数学工具是为了达到目的而选择的操作手段，是认知操作过程的一部分，是认知操作手段的延伸和拓展，是进行问题解决学习不可或缺的工具。数学工具在辅助问题解决学习中具有以下特点：第一，形象性。借助数学工具可以形象地展示数学概念、规律。第二，实时性。数学工具可以随时根据学习的需要展示数学对象。第三，替代性。数学工具可以替代中职生开展计算、作图、制表等工作。

二、中职生使用数学工具进行数学问题解决学习的基本程序

“数学问题解决教学是通过创设问题情境，激发学生的求知欲望，使学生亲身体验和感受分析问题、解决问题的全过程。它强调使用数学的意识，培养学生的探索精神、合作意识和实际操作能力。”运用数学工具进行问题解决教学程序包括以下六个环节。

（一）基于问题解决的教学设计

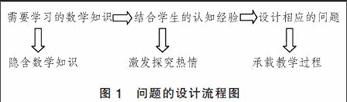
问题解决在问题空间中进行搜索，由一定的情景引起的，按照一定的目标，应用各种认知活动、技能等，经过一系列的思维操作，使问題得以解决的过程。问题的设计是整个教学过程的关键。所提出的问题既要激发学生的学习兴趣，又要包括即将学习的数学知识，且能引导学生自主探究不断深入。关于问题的设计流程如下图：

图1 问题的设计流程图

（二）数学知识的应用准备

数学知识包括数学的概念、公式、定理、运算方法等。此处的知识传授，有别于传统的教学模式，通过反复训练，强化知识认知。这样的模式固然强化了基础，然而却牺牲了学生的问题意识、创造思维和应用能力的培养。本模式则强调通过问题的引导，教师指导学生经过查找、思维等过程，亲身体会知识产生的过程，这样的学习具有灵活性和可变通性。

（三）建立问题解决数学模型

数学模型（Mathematical Model）是将现实问题归结为相应的数学问题，并在此基础上利用数学的概念、方法和理论进行深入的分析和研究，从而从定性或定量的角度来刻画实际问题，并为解决现实问题提供精确的数据或可靠的指导。通常用字母、数字及其它数学符号建立起来的等式或不等式以及图表、图像、框图等描述客观事物的特征及其内在联系的数学结构表达式。建立数学模型就是沟通现实问题和数学知识、数学工具的必要途径。

（四）确定数学工具和操作路径

当建立在数学知识基础之上的数学模型一经确立，解决这个模型对应的问题，需要学生寻找合适的数学工具。如模型是二次函数最值问题，可以选择几何画板中的作图工具，很容易地获得结果。而无需运用二次函数图像法求最值或配方法求最值，因为这些方法对于多数中职生是难以理解的，更无从运用它们解决问题。借助工具，不仅可以帮助学生克服因解决数学模型带来的思维障碍，更可以帮助学生顺利地发展建模思维。