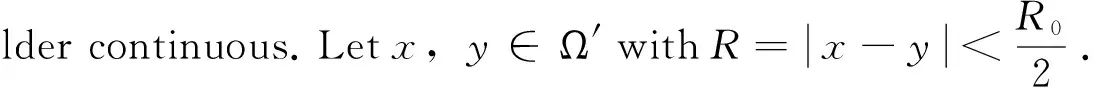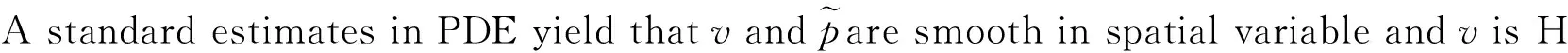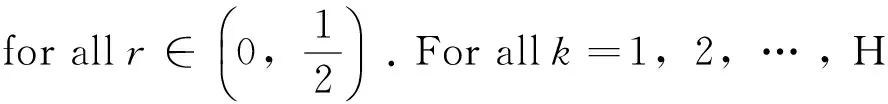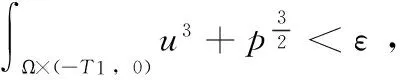The regularity of Navier-Stokes equations in five-dimensional space

2017-05-18

中山大学学报(自然科学版)(中英文) 2017年1期

关键词：马西维空间国家自然科学基金

(Graduate School of China Academy of Engineering Physics, Beijing 100088, China)

MAXixia

(Graduate School of China Academy of Engineering Physics, Beijing 100088, China)

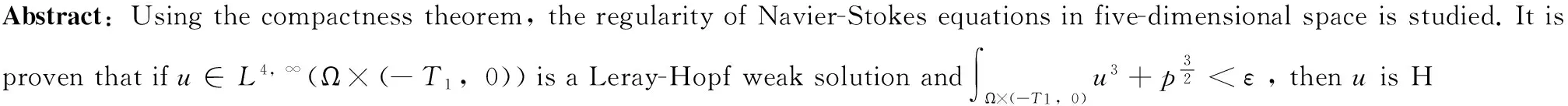
five dimensional space; Navier-Stokes; compact theorem; Hölder continuous

This paper is concerned with the partial regularity of weak solutions of incompressible Navier-Stokes equations in five dimensional space with unit viscosity and zero external force:

(1)

forx∈Ω⊆R5,t<0, and

(2)

The concepts of weak solutions of (1)-(2), and their regularity were already introduced in the fundamental paper of J.Leray. Pioneering works of J. Leray showed the existence of a functionuandpsuch that

(iii)usatisfies the Navier-Stokes equations in the distribution sense.

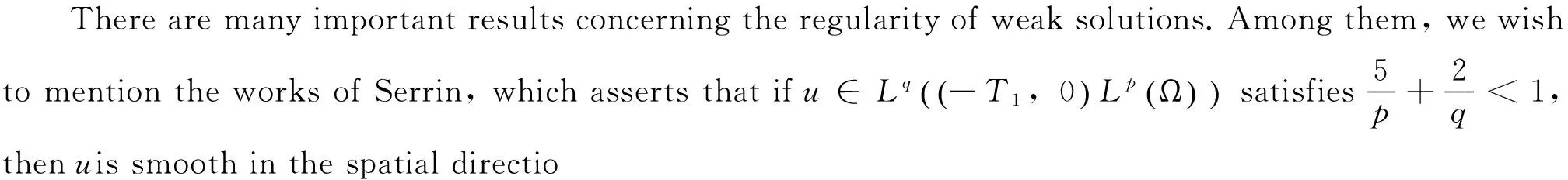
In the series of papers [1-2,4-5], when the spatial dimensiondis 3, Scheffer introduced the notions of suitable weak solutions and the generalized energy inequality. He also established various partial regularity results of such weak solutions. Scheffer’s results were further generalized and strengthened in the paper of Caffareli, Kohn and Nirenberg[2], ford=3.

Ford=4,V.Scheffer[6]provedthatthereexistsaweaksolutionuinR4×RsuchthatuiscontinuousoutsidealocallyclosedsetofR4×Rwhose3-DHausdorffmeasureisfinite.Ford=5,6,Struwe[2],DuandDong[3]obtainedthecorrespondingresultsinthesteadyNavier-Stokesequations.TianandXin[7]showedthepartialregularityforsmoothsolutionsandanyspatialdimensioninthesteadyNavier-Stokesequations.

1 The Compactness theorem

Definition 1 Let Ω be a open set in R5. We say that a pair (u,p)isasuitableweaksolutiontotheNavier-StokesequationsonthesetΩ×(-T1,0)ifitsatisfiestheconditions:

(i)

u∈L2,∞(Ω×(-T1,0))∩L2(-T1,0;H1(Ω)),

(3)

(ii)uandpsatisfytheNavier-Stokesequationsinthedistributionsense;

(iii)uandpsatisfythelocalenergyinequality

(4)

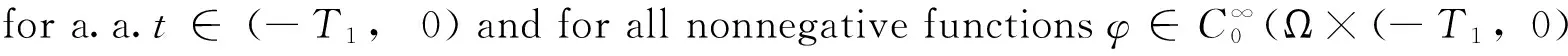
Theorem 1[5]LetX0,XandX1bethreeBanachspacesandXi(i=0,1)isreflectivesuchthat

X0⊆X⊆X1

theinjectionofXintoX1beingcontinuous;andtheinjectionofX0intoXiscompact.LetTbeafixednumber,andletα0,α1betwofinitenumberssuchthatαi≥1,i=0,1.

Weconsiderthespace

AndthespaceΥisprovidedwiththenorm

ThentheinjectionofΥintoLα(0,T;X)iscompact.

Lemma 1 Let (u,p)isaweaksolutionoftheCauchyproblemsoftheNavier-StokesequationsinΩwithu∈L2,∞(Ω×(-T1,0))∩L2(-T1,0;H1(Ω)).Inaddition,

u∈L4,∞(Ω×(-T1,0))

(5)

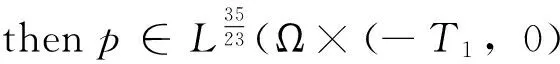
Proof First by using Holder inequality and Young inequality,

(6)

In fact, by interpolation inequality,

Andthenweknow

(7)

inanyopensetΩ⊆R5fora.e.t∈(-T,0).

By the elliptic regularity theory,

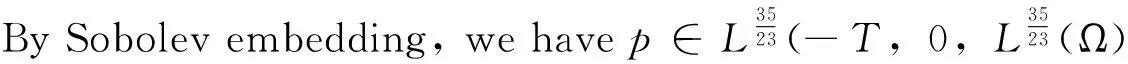
Theorem 2 Let (un,pn)isasequenceofweaksolutions(1)-(2)inΩ×(-T,0)satisfying:

Supposethat(u,p)isaweaklimitof(un,pn),then(u,p)isalsoasuitableweaksolutionof(1)-(2).

Proof In fact, we can choose a subsequence

(8)

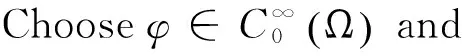
(∂tun,φ)=-(un·▽un,φ)-(▽un,▽φ)≤

Hence

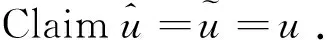
In the following we prove in two steps.

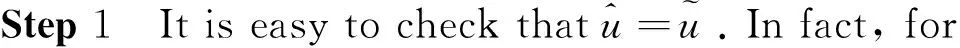
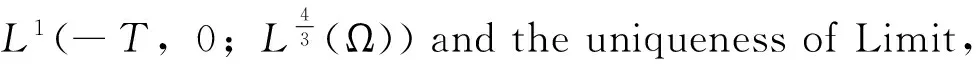
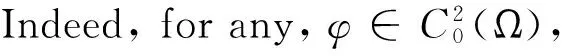
asδ→0,o(1)→0

And

ο(1)asn→0,ο(1)→0

Accordingtotheweakcontinuousint,

asδ→0,ο(1)→0isindependentofn.

Hence,

FinallybyTheorem1,

un→u

(9)

convergesstronglyinL2(Ω×(-T,0)). Also,u∈L4,∞(Ω×(-T,0)),byinterpolationinequality,

Hencefrom(9),

un→u

(10)

convergesstronglyinL3(Ω×(-T,0)). Since (u,p)istheweaklimitof(un,pn), for any smoothφ>0compactlysupportedinΩ×(-T,0), we have that

From Lemma 1 and (10), the theorem is proved.

2 The Regularity theorem

Using the compactness theorem in the last section, we show the partial regularity of the weak solutions of (1)-(2). Here we give a result which characterizes Hölder continuous functions by the growth of their local integrals.

Theorem 3 Supposeu∈L2(Ω)satisfies

(11)

foranyBr(x)⊆Ωandα∈(0,1),where

thenu∈Cα(Ω).

Proof DenoteR0=dist(Ω′,∂Ω),Ω′⊆Ω. For anyx0∈Ω′and0

andintegratingwithrespecttoxinBr1(x0)

from(11),

(12)

andthereforeforh

with

forany0

for anyx∈Ω′ andR≤R0. Henceuis bounded in Ω′withtheestimate

Then we have

The first two terms on the right sides are estimated in (11). For the last term we write

and integrating with respect toζoverB2R(x)∩B2R(y),whichcontainsBR(x),yields

Therefore,wehave

Inthefollowingweassume(u,p)isasuitableweaksolutionofNavier-StokesequationsinΩ×(-T1,0).

Lemma 2 Suppose (u,p)isasuitableweaksolutionof(1)-(2),ifthereexiststwopositiveconstantε0suchthat

(13)

and

u∈L4,∞(Ω×(-T,0))

(14)

then

(15)

for-θ2≤t≤0.DenoteQθ=Bθ×(-θ2,0).

Proof Suppose that Lemma 2 is false, then there is a subsequence of weak solutions (ui,pi)with

(16)

whereQ1=B1×(-1,0),andsuchthat(15)isnotvalidfor(ui,pi).Let

then

(17)

▽vi)

(18)

inQ1. By Fatou Lemma,

Sinceun→uisstrongconvergeinL3(Q), we have

(19)

for all sufficiently enoughi.

(20)

Here

(21)

and

Denote

thenbyCalderon-Zygmundestimateand(20),

(22)

Hencefrom(20),(22),(23),weget

(24)

Itisobviousfrom(24)that

(25)

Combining (19) and (25), we obtain a contraction and the lemma is proved.

Theorem 4 Under the assumptions of Lemma 2, then for any numberk,▽k-1uisHöldercontinuousinsubsetK⊂⊂Ω×(-T,0)andthefollowingboundisvalid:

wherec0isaconstantonlydependingonk.

Proof Let (u,p)beasuitableweaksolutionsuchthat

Let

Asimplecomputationyieldsthatis(u1,p1)asuitableweaksolutionof

▽u1+▽p1=0

Moreover,Lemma2impliesthat

WerepeatthesameargumentsasLemma2 ,itisconcludedthat

isboundedbyanabsoluteconstant.

Thecasek>1istreatedwiththehelpoftheregularitytheoryfortheStokesequationsandbootstraparguments.

Reference：

[1] ESCAURIAZA L, SEREGIN G, SVERáK V.OnL3,∞-solutions to the navier-stokes equations and backward uniqueness [J]. Retrieved from the University of Minnesota Digital Conservancy, 2002. http://hdl.handle.net/11299/3858.

[2] STRUWE M. On partial regularity results for the Navier-Stokes equations [J]. Comm Pure Appl Math, 1988,41(4):437-458.

[3] DONG H, DU D. Partial regularity of Solutions to four-dimmensional Navier-Stokes equations at the first blow-up time [J].Comm Math Phys, 2007, 273(3): 785-801.

[4] CAFFARELLI L, KOHN V, NIRENBERG L. Partial regularity of suitable weak solutions of the Navier-Stokes equations [J]. Comm Pure Appl Math, 1982, 35(6): 771-831.

[5] LIN F. A new proof of the Caffarelli-Kohn-Nirenberg theorem [J]. Comm Pure Appl Math, 1998, 51(3): 241-257.

[6] SCHEFFER V. Partial regularity of solutions to the Navier-Stokes equations[J]. Pacific Journal of Mathematics, 1976, 66(2):535-552.

[7] TIAN G, XIN Z. Gradient estimation on Navier-Stokes equations [J]. Comm Anal Geom, 1999, 7(2): 221-257.

[8] KATO T. StrongLp-solutions of the Navier-Stokes equations in Rm with applications to weak solutions [J]. Math Zeit, 1984, 187: 471-480.

[9] SEREGIN G. Differentiability properties of weak solutions to the Navier-Stokes equations [J]. Algebra and Analysis, 2002, 14: 193-237.

[12] SERRIN J. On the interior regularity of weak solutions of the Navier-Stokes equations [J]. Archive for Rational Mechanics and Analysis, 1962, 9(1):187-195.

[13] 张双虎，冯兆永，杨凯波. 修正Camassa-Holm方程的Cauchy问题[J]. 中山大学学报(自然科学版), 2014, 53(4): 8-12. ZHANG S H, FENG Z Y, YANG K B. The Cauchy problem for the modified Camassa-Holm equations [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2014, 53(4): 8-12.

[14] 赵继红，冯兆永. 具有临界增长边界条件的p-Laplace方程解的存在性[J]. 中山大学学报(自然科学版), 2010, 49(1):1-4. ZHAO J H, FENG Z Y. Existence of weak solutions for thep-Laplace equation with critical growth in boundary conditions [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49(1):1-4.

[15] 关春霞，冯兆永. 弱耗散的Degasperis-Procesi方程弱解的存在性[J]. 中山大学学报(自然科学版), 2014, 53(2): 49-54. GUAN C X, FENG Z Y. The existence of global entropy weak solutions for a weakly dissipative Degasperis-Procesi equation [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2014, 53(2): 49-54.

五维空间Navier-Stokes方程的正则性*

2016-09-19 基金项目：国家自然科学基金 (11671045)

马西霞(1990年生)，女；研究方向：流体方程；E-mail:kfmaxixia@163.com

马西霞

(中国工程物理研究院研究生院，北京 100088)