多传感器交叉提示技术及其在目标跟踪中的应用
2017-05-18黄树彩刘锦昌
庞 策,黄树彩,刘锦昌,赵 炜
(空军工程大学防空反导学院,西安710051)
多传感器交叉提示技术及其在目标跟踪中的应用
庞 策,黄树彩,刘锦昌,赵 炜
(空军工程大学防空反导学院,西安710051)
针对传感器交叉提示在目标跟踪中的应用问题,围绕如何通过传感器交叉提示技术实现“传感器资源管理”、“提高目标跟踪精度”和“实现目标交接”展开研究,提出传感器网络效能评价函数,分析不同类型的交叉提示发生的时机与条件,设计基于博弈论的多传感器交叉提示算法,并提出基于假设检验理论的传感器博弈策略调整方法。仿真结果表明,本文提出的多传感器交叉提示模型符合实际作战场景,能够顺利实现传感器管理、提高目标跟踪精度和进行目标交接,与粒子群算法、合同网算法和拍卖算法相比,博弈论算法具有较好的求解质量,收敛速度明显提高。
多传感器交叉提示;博弈论;那什均衡;假设检验
0 引 言
多传感器交叉提示[1-2]属于多传感器协同任务规划[3]的重要内容,在导弹预警探测系统中,将每个传感器看作具有自主行为的智能体[4],传感器对目标信息相互提示,对目标协同探测,以此实现传感器-目标分配、目标跟踪精度提高和目标交接。
多传感器交叉提示技术研究的重要内容为“提示谁”的问题,即由哪些传感器针对目标组建探测联盟[5],这就是多传感器交叉提示算法。针对此问题,文献[2]提出改进粒子群算法、文献[6]采用匈牙利算法、文献[7]提出粒子群拍卖混合算法,此类方法为集中式算法。另一类为分布式算法,主要有文献[9]提出合同网算法、文献[10]提出的拍卖算法、文献[11]提出的分布式一致方法、文献[12]提出的基于谈判机制的任务分配方法、文献[13]提出的扩展合同网算法、以及文献[14]提出的改进拍卖算法。与集中式算法相比,分布式算法具有求解速度快、通信代价小、容错能力强等优点,更适应瞬息万变的战场环境,但其求解质量欠佳[8],如何在保证分布式算法求解速度的条件下同时提高求解质量,成为近几年研究的热点与难点。。
本文围绕多传感器交叉提示技术及其在目标跟踪中的应用展开研究,重点讨论如何通过多传感器交叉提示,开展传感器管理、提高目标跟踪精度、进行目标交接等问题,研究传感器联盟的动态变化过程,提出基于博弈论和假设检验理论的多传感器交叉提示算法,将提出的算法与已有文献中的粒子群算法、合同网算法和拍卖算法进行了比较。
1 传感器网络性能指标
1.1 传感器网络效能模型
设传感器网络中共有m个传感器,需要同时对n个目标进行跟踪,传感器—目标配对矩阵为X,其元素为xij,当传感器si对目标tj进行跟踪时,xij=1,否则,xij=0。
若xij=1,则传感器si取得的效能为:
qij=αpij+βcij
(1)
式中:α>0、β>0为加权系数,且α+β=1;qij为si跟踪tj时的效能,pij为si对tj的跟踪精度,称为收益;cij为si对tj传感器资源消耗,称为能耗。
目标函数为传感器网络整体效能最大,即:
(2)
约束条件为每个传感器实际跟踪目标个数小于能够同时跟踪目标的最大个数。
1.2 目标实际跟踪精度计算模型
本文将跟踪精度定义为几何精度衰减因子[14]的负数,其计算式为:
(3)
式中:P(k|k)为k时刻误差协方差矩阵。
对目标t进行跟踪,其跟踪精度计算模型分两种情况进行讨论:
1)仅有1个传感器跟踪tj的情况
设目标的离散状态方程为:
Xk+1=ΦXk+ΓWk
(4)
传感器量测方程为:
Zk=HXk+Vk
(5)
式中:Xk为k时刻的状态向量,Xk+1为k+1时刻的状态向量,Φ为状态转移矩阵,Γ为过程噪声分布矩阵,Wk为系统噪声,Zk为k时刻的量测向量,H为量测矩阵,Vk为量测噪声。
在目标跟踪中,采用扩展卡尔曼滤波对目标状态进行估计,卡尔曼滤波迭代计算式为[15]:
(6)
2)有M个传感器同时跟踪t的情况
这种情况为多传感器信息融合问题。当有M个传感器同时对t进行跟踪时,各传感器对该目标的量测方程为[16]:
(7)
令
(8)
此时,有Zk=HXk+Vk,此后的滤波形式与式(6)相同。
1.3 传感器网络能耗计算模型
当使用传感器si对目标进行探测时,能耗为:
(9)
式中:α1和β1为常数,取α1=0.01、β1=0.1,l(si)为传感可同时跟踪的目标个数,r(si)为传感器最大探测距离。
1.4 目标跟踪精度需求
目标跟踪精度需求p*为作战指挥控制中心所期望的对目标跟踪精度应达到的值。需要考虑提高传感器跟踪精度的情况有:
1)目标交接过程中,应满足接管目标传感器捕获目标时对目标的跟踪精度要求。
2)拦截弹发射时,应满足武器系统对目标的跟踪精度需求。
3)目标进入我方安全警戒区域,由远及近向我方飞行时,对我方威胁不断增大。
2 传感器交叉提示类型
传感器提示分为“信息提示”和“任务提示”,“信息提示”即信息共享,指一个传感器将关于目标的速度等信息传递给其它传感器;“任务提示”指当一个传感器对目标的量测结果达不到作战要求时,提示其它传感器对目标进行探测。本文主要研究对象为“任务提示”,根据提示目的不同,将“任务提示”分为以下三种:
类型一:开展传感器资源管理
当多个目标同时来袭时,假定在时间片段内,目标静止不动,传感器网络应制定最优的多目标—多传感器分配方案,使传感器网络效能较高,此种情况下,传感器交叉提示算法可以看作是一种分布式多目标—多传感器分配算法。针对目标t组建传感器联盟,发生交叉提示的传感器为能够同时探测到t的传感器集合。
类型二:提高目标跟踪精度
传感器对目标进行跟踪时,若不考虑目标跟踪精度需求而一味提高传感器网络效能,可能出现传感器网络虽然效能很大,但单目标跟踪精度却很低的情况,达不到作战指挥控制中心对单目标的跟踪精度需求,这在实战中没有意义。本文中,设若对目标的实际跟踪精度p小于跟踪精度需求p*,则令p=0,传感器对目标的探测不产生收益,仅造成能耗。对于目标t来说,发起提示的传感器为针对目标t进行跟踪的传感器联盟中的传感器,被提示传感器为传感器联盟外能够探测到目标t的传感器。
类型三:实现目标交接
当目标在运动过程中将要“逃离”传感器的探测区域时,传感器将会产生“任务提示”需求,提示其它传感器对目标进行跟踪,从而实现对目标跟踪任务的交接。
设在k时刻,目标t和sa的距离为da(k),目标t和sb的距离为db(k),在k+1时刻,目标t和sa的距离为da(k+1),目标t和sb的距离为db(k+1)。sa在对目标进行探测过程中,当da(k+1)>da(k)且da(k)>0.7ra时,sa将会产生提示需求,将会提示其它传感器接管对目标的探测任务;当db(k+1) 3.1 两个传感器博弈模型 当目标t同时位于两个传感器sa和sb的探测范围内时,由最早探测到目标t的传感器sa产生“任务提示”需求。对于sb来讲,若其不对t进行探测,仍可通过sa的“信息提示”获得由sa探测到的关于目标的信息,此时sb的效能为qb=αpa;若sa和sb同时对t进行探测,则sb的效能为qb=αpab+βcb;当仅由sb对t进行探测,则sb的效能为qb=αpb+βcb;当sa和sb均不对t进行探测时,sb的效能qb=γ,γ为常数,远远小于其它三个值,以确保每个目标都有传感器对其进行跟踪。sb的博弈矩阵如下所示[17-18]: (10) 式中:C表示“合作策略”,D表示“背叛策略”。 1)当传感器交叉提示的目的是开展传感器资源管理时,应有: (1)αpab+βcb>γ,即博弈个体倾向于共同合作(C,C),而非共同背叛(D,D); (2)αpab+βcb>αpb+βcb,即传感器倾向于共同合作(C,C),而非单方面合作(D,C); (3)αpa>γ且αpb+βcb>γ,即两个传感器至少有一个采取合作的策略(D,C)或(C,D),保证目标能够被至少一个传感器探测。 此种情况下那什均衡状态不能由分析得到。 2)当传感器交叉提示的目的是提高目标跟踪精度时,除满足以上三个((1)、(2)、(3))条件外,接受提示的传感器sb应满足αpab+βcb>αpa,即那什均衡状态为(C,C),此时传感器倾向于共同合作(C,C),为使传感器倾向于合作,以此提高目标跟踪精度,在计算过程中,应增大α的值,减小β的值。 3)当传感器交叉提示的目的是进行目标交接时,sa选择D策略,此时,sb选择C策略。 3.2 多个传感器博弈模型 当目标t位于M个传感器的探测范围内时,传感器集合为{s1,s2,…,sM},此种情况下,当sa进行博弈时,博弈sb可以看作为{s1,s2,…,sM}-sa组合而成的“虚拟传感器”,其中任意一个传感器选择C策略,则该“虚拟传感器”为C策略。 3.3 传感器博弈策略更新规则 初始化各个传感器初始状态,设H(T)=1,表示传感器sb在第T次迭代时采取C策略,该传感器效能增大;H(T)=0,表示传感器sb在第T次迭代时采取D策略,该传感器效能增大。设在第T次迭代时采取C策略的概率为Q(T),传感器博弈过程中,倾向于合作,采取C策略效能增加的概率为O(T)(0.5 1)当qb(T)≥qb(T-1)时,则按下式更新: 第T次迭代后sb策略更新后收益增加的概率为: U(T)=Q(T)×O(T)+ (1-Q(T))×(1-O(T)) (11) 第T+1次迭代时, (12) 当0.5 2)当qb(T) 第T次迭代后sb策略更新后收益减小的概率为: U-(T)= (1-Q(T))×O(T)+ Q(T)×(1-O(T)) (13) 第T+1次迭代时, (14) 当0.5≤O(T)≤1时,有O 3.4 算法步骤 确定博弈传感器集合{s1,s2,…,sM}后,基于博弈论和假设检验理论的算法流程图如图1所示。 设敌方基地坐标(2000,2000),某一时刻同时发射3枚导弹t1、t2、t3,分别攻击我方城市A、B、C,其坐标分别为(100,800)、(300,300)、(500,100),论文中坐标单位均为km,导弹速度为1800km/h,导弹运动轨迹、防护城市及传感器位置分布如图2所示。 论文中,传感器性能如表1所示,传感器网络中各传感器类型如表2所示。 4.1 单目标情形仿真 1)开展传感器资源管理 当k=0.2h时,t1位置为(1692,1807),此时能够探测到t1的传感器集合为{s1,s2,s3,s4,s5},传感器网络初次分配传感器对该目标进行跟踪。采用本文算法计算分配方案,计算传感器网络效能时,取α=0.1,β=0.9,博弈过程中,取γ=-20。传感器博弈过程如图3所示。 以T=1和T=2时说明传感器博弈过程。 T=1时,(1)随机确定传感器博弈策略,有:G(T=1)={D,D,C,D,D}。 (2)经计算,各传感器效能有:q(T=1)={-0.34,-0.69,-0.50,-0.39,-0.72},博弈矩阵为: (3)给定T=2时的传感器策略更新规则,有: Q={0.50,0.50,0.50,0.50,0.50}、O={0.2,0.8,0.2,0.8,0.8}。 T=2时,(1)按照策略更新规则更新传感器博弈策略,有:G(T=2)={C,D,D,C,D}。 (2)经计算,各传感器效能有:q(T=2)={-0.38,-0.64,-0.48,-0.33,-0.69},博弈矩阵为: (3)更新T=3时的传感器策略更新规则,有:Q={0.52,0.47,0.47,0.59,0.34}、O={0.8,0.2,0.2,0.8,0.2}。 经过15次博弈计算后,最终采取C策略的传感器为s1、s2、s5,采取D策略的传感器为s3、s4。 进行100次蒙特卡洛试验,5个传感器在博弈过程中,博弈策略变化曲线如图4 (a)所示,其中,纵坐标“0”表示D策略,“1”表示C策略,传感器效能变化曲线如图4(b)所示,传感器网络效能变化曲线如图4 (c)所示,对目标跟踪的传感器变化如图4(d)所示。 表1 传感器特性Table 1 The ability of sensors 表2 传感器部署类型及其位置Table 2 Types of sensors and their positions 2)提高目标跟踪精度 当k=0.4h时,t1位置为(1386,1615),可探测t1的传感器集合为{s1,s2,s3,s4,s5},跟踪该目标的传感器为s2,跟踪精度为-2.1972,传感器网络效能为-1.2228,此时,作战指挥控制中心对t1提出跟踪精度需求为-1.5,s2产生提示需求,被提示传感器为{s1,s3,s4,s5}。令α=0.5,β=0.5,采用本文算法进行仿真,对t1的跟踪精度变化曲线和传感器网络能耗变化曲线见图5。 经过6次迭代计算,最终采取C策略的传感器为s1、s3、s4,采取D策略的传感器为s3、s4,即对t1进行跟踪的传感器为s1、s3、s4,跟踪精度为-1.43,达到了作战指挥控制中心提出的跟踪精度需求。按照α=0.1,β=0.9,该方案中,传感器网络能耗为-3.28,比计算之前有所下降;按照α=0.5,β=0.5,该方案中,传感器网络能耗为-1.20,比计算之前有所上升。可知,目标跟踪精度的提高,是以牺牲传感器资源为代价的。 3)实现目标交接 当k=0.75h时,t1位置为(848,1279),可探测该目标的传感器集合为:{s1,s2,s3,s4,s5,s9,s10,s11,s12,s13,s14,s15,s17,s18},此时,对t1跟踪的传感器 为s9,目标交接过程如下所述: (1)k=0.75h,s9与t1的距离d1(0.75)=895.6km>0.7r1=700km,此时s9满足目标交接条件,将提示其它传感器对目标进行交接。 (2)满足被提示条件的传感器集合为{s10,s11,s12,s14,s15}。 (3)s9与集合{s10,s11,s12,s14,s15}中的传感器进行博弈,采用本文算法确定接替s9对目标跟踪的传感器,在博弈过程中,s9的博弈策略为D策略不变。 取α=0.1,β=0.9。进行100次蒙特卡洛试验,6个传感器在博弈过程中,博弈策略变化曲线如图6 (a)所示,其中,纵坐标“0”表示D策略,“1”表示C策略,传感器效能变化曲线如图6(b)所示,传感器网络效能变化曲线如图6(c)所示,对目标跟踪的传感器变化如图6(d)所示。 最终采取C策略的传感器为s11、s14、s15,采取D策略的传感器为s10、s12,即对t1跟踪的传感器为s11、s14、s15,传感器网络效能为-3.89,最终方案确定后,s9不再对目标跟踪,完成目标交接。 4.2 多目标情形仿真 1)传感器初次分配过程仿真 当k=0.2h时,目标坐标为t1(1696,1769)、t2(1593,1644)、t3(1456,1371),能够探测到3个目标的传感器为{s1,s2,s3,s4,s5}。 在计算传感器网络效能时,取α=0.5,β=0.5,分别用本文中的博弈论算法、文献[2]中的粒子群算法、文献[13]中的合同网算法和文献[14]中的拍卖算法计算传感器联盟方案,进行100次蒙特卡洛试验,传感器网络效能与迭代次数的变化关系如图7(a)所示,各算法运行时间如图7(b)所示。 由图7可知,在博弈论算法、合同网算法和拍卖算法三种分布式算法当中,博弈论算法收敛速度最快、求解质量最高,与粒子群算法集中式算法相比,其求解质量几乎相同。 2)多目标跟踪过程仿真 目标整个飞行过程中,分别用四种算法计算网络能耗变化曲线如图8(a)如示,t1跟踪精度变化曲线如图8(b)如示,t2跟踪精度变化曲线如图8(c)如示t3跟踪精度变化曲线如图8(d)如示。 由图8可知,四种算法性能从高到低依次为:博弈论算法、拍卖算法、合同网算法、粒子群算法。 本文围绕如何通过传感器交叉提示技术实现“传感器资源管理”、“目标跟踪精度提高”和“目标交接”等目标而展开,首先建立了传感器网络效能函数,其次根据任务不同将传感器交叉提示分类,讨论了三种类型的传感器提示在传感器联盟组建、更正和更新中的作用,设计了基于博弈论的多传感器交叉提示算法,提出基于假设检验理论的传感器博弈策略更新方法,最后进行了仿真校验。仿真结果表明,本文提出的多传感器交叉提示模型符合实际作战场景,能够顺利实现传感器管理、提高目标跟踪精度和进行目标交接,与代表集中式算法的粒子群算法和代表分布式算法的合同网算法和拍卖算法相比,博弈论算法收敛速度明显提高,求解质量较高,在作战态势变化较快的情形下具有明显优势。 [1]StrombergD.Asensor-independentsensor-orientedtrackingarchitecture[C]. 1999IEEEInformationDecisionandControlConference,Adelaide,Australia,April13-18, 1999. [2] 樊浩, 黄树彩, 高美凤, 等. 多传感器交叉提示多目标探测动态联盟技术研究[J]. 宇航学报, 2011, 32(11): 2381-2386. [FanHao,HuangShu-cai,GaoMei-feng,etal.Researchontechniqueofmulti-targetdetectionusingmulti-sensorcross-cueingbasedondynamiccoalition[J].JournalofAstronautics, 2011, 32 (11): 2381-2386.] [3] 李志汇, 刘昌云, 倪鹏, 等. 反导多传感器协同任务规划综述[J]. 宇航学报, 2016, 37(1):29-38. [LiZhi-hui,LiuChang-yun,NiPeng,etal.Reviewonmulti-sensorcooperativemissionplanninginanti-TBMsystem[J].JournalofAstronautics, 2016, 37(1): 29-38.] [4]MengDY,JiaYM,DuJP,etal.High-precisionformationcontrolofnonlinearmulti-agentsystemswithswitchingtopologies:alearningapproach[J].InternationalJournalofRobustandNonlinearControl, 2015, 25 (13): 1993-2018. [5] 刘梅, 李海昊, 沈毅. 无线传感器网络空中目标跟踪任务分配技术的研究[J]. 宇航学报, 2007, 28(4):960-965. [LiuMei,LiHai-hao,ShenYi.Studyallocationofairtargettrackingtaskinwirelesssensornetwork[J].JournalofAstronautics, 2007, 28(4): 960-965.] [6] 童俊, 单甘霖. 基于Cramér-Rao下限的多传感器跟踪资源协同分配[J]. 宇航学报, 2012, 33(9):1314-1321. [TongJun,ShanGan-lin.Multi-sensortrackingresourcecoordinatedallocationbasedonCramér-Raolowbound[J].JournalofAstronautics, 2012, 33(9): 1314-1321.] [7] 费爱国, 张陆游, 刘刚, 等. 基于粒子群拍卖混合算法的空空导弹制导权移交技术[J]. 宇航学报, 2013, 34(3): 340-346. [FeiAi-guo,ZhangLu-you,LiuGang,etal.Thetechniqueforair-to-airmissileguidancesuperiorityhandoverbasedonparticleswarmauctionhybridalgorithm[J].JournalofAstronautics, 2013, 34 (3): 340-346.] [8] 段沛博, 张长胜, 张斌. 分布式约束优化方法研究进展[J]. 软件学报, 2016, 27(2):264-279. [DuanPei-bo,ZhangChang-sheng,ZhangBin.Researchprogressindistributedconstraintoptimizationmethod[J].JournalofSoftware, 2016, 27(2): 264-279.] [9]DoruP,CarlosP.Anextendedcontractnetprotocolwithdirectnegotiationofmanagers[M].NewYork:Springer, 2014. [10]ZhongL,HuangQ,WuF,etal.Trade:Atruthfulonlinecombinatorialauctionforspectrumallocationincognitiveradionetworks[J].WirelessCommunication&MobileComputing, 2015, 15 (9): 1320-1330. [11]SeversonTA,DerekAP.Distributedmulti-targetsearchandtrackassignmentwithconsensus-basedcoordination[J].IEEESensorsJournal, 2015, 15 (2): 864 -875. [12]YanK,ZhangMJ,YeDY.Anegotiation-basedmethodfortaskallocationwithtimeconstraintsinopengridenvironment[J].ConcurrencyandComputation:PracticeandExperience, 2015, 27 (3): 735-761. [13]AmarKG,GuyEG.Equivalenceclassverificationofthecontractnetprotocolextension[J].InternationalJournalonSoftwareToolsforTechnologyTransfer, 2016, 18(6): 685-706. [14] 方德亮, 冉晓旻, 李鸥. 一种能量有效的分布式传感器管理算法[J]. 西安电子科技大学学报(自然科学版), 2017, 44(2):182-187. [FangDe-liang,RanXiao-min,LiOu.Energyefficientdistributedsensormanagementalgorithm[J].JournalofXidianUniversity, 2017, 44(2): 182-187.] [15]BasileM,LudovicC.Real-timeupdatingofstructuralmechanicsmodelsusingKalmanfiltering,modifiedconstitutiverelationerror,andpropergeneralizeddecomposition[J].NumericalMethodinEngineering, 2016, 107(9): 786-810. [16]WhiteK,WilliamsJ,HoffensetzP.Radarsensormanagementfordetectionandtracking[C].Proc.ofIEEEInternationalConferenceonInformationFusion,Nice,France,September22-26, 2008. [17]VonNeumannJ,MorgensternO.Theoryofgamesandeconomicbehavior(60thAnniversaryCommemorativeEdition)[M].Princeton:Princetonuniversitypress, 2007. [18]HamedK,NasserY.Gameoftheoryconsumptionbalancinginheterogeneoussensornetworks[J].WirelessCommunicationandMobileComputing, 2016, 16(12): 1457-1477. 通信地址:陕西省西安市长乐东路甲字一号学(710051) 电话:18392447996 E-mail:18392447996@163.com (编辑:牛苗苗) Multi-Sensor Cross Cueing Technology and Its Application in Target Tracking PANG Ce, HUANG Shu-cai, LIU Jin-chang, ZHAO Wei (Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China) For the application of the multi-sensor crossing cueing technology to target tracking, how to manage the sensors, improve the tracking accuracy and transfer the targets by using the multi-sensor crossing cueing technology is taken into consideration. The energy consumption function of the sensors is raised. The time and requirements of different types of the cross cueing are analyzed. The multi-sensor crossing cueing algorithm based on game theory is designed, with the adapting method of gaming strategy based on hypothesis testing being raised. Simulation result indicates that the proposed model conforms to the battles reality, and by the game algorithm, the tasks of managing sensors, improving the tracking accuracy and transferring targets can be completed. In comparison with the particle swarm algorithm, contract net algorithm and auction algorithm, the game algorithm has better result and its convergence rate is improved. Multi-sensor cross-cueing; Game theory; Nash equilibrium; Hypothesis testing 2016-12-19; 2017-02-09 国家自然科学基金(61573374);青年国家自然科学基金(61503408);航空科学基金(20150196006) TN215 A 1000-1328(2017)04-0401-09 10.3873/j.issn.1000-1328.2017.04.010 庞 策(1993-),男,硕士生,主要从事多传感器交叉提示技术研究。3 传感器交叉提示算法
4 仿真校验
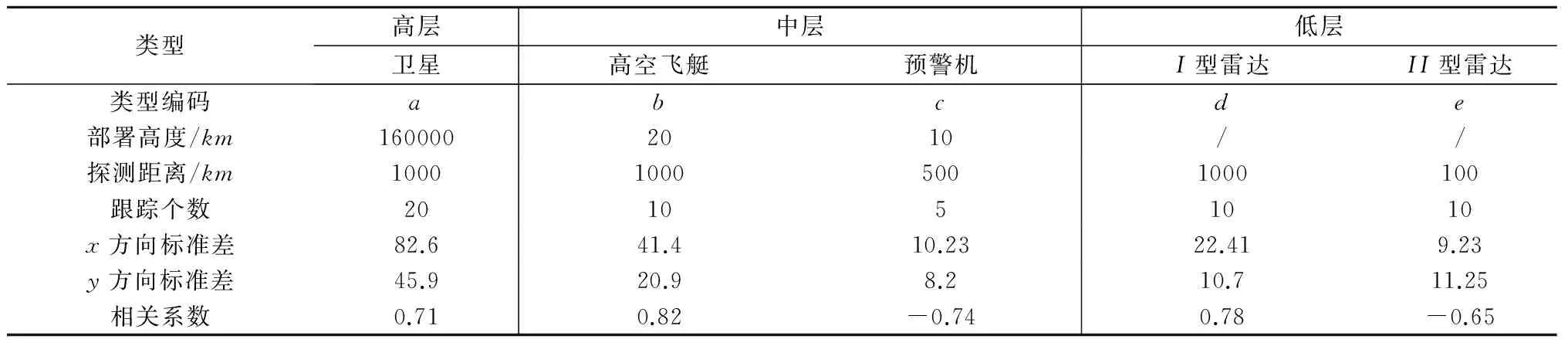
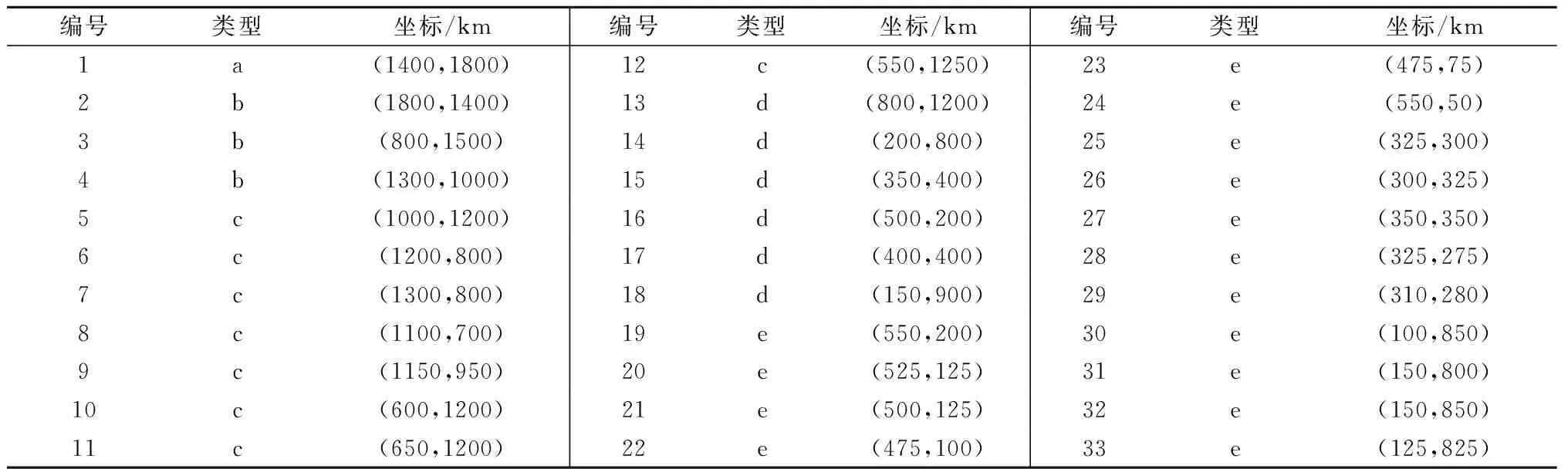
5 结 论
