一种计算三体问题周期轨道的新方法
2017-05-18泮斌峰
郑 越,泮斌峰,3,唐 硕,3
(1. 西北工业大学航天学院,西安710072;2. 陕西省空天飞行器设计重点实验室,西安710072;3. 航天飞行动力学技术国家级重点实验室,西安710072)
一种计算三体问题周期轨道的新方法
郑 越1,2,泮斌峰1,2,3,唐 硕1,2,3
(1. 西北工业大学航天学院,西安710072;2. 陕西省空天飞行器设计重点实验室,西安710072;3. 航天飞行动力学技术国家级重点实验室,西安710072)
针对三体问题周期轨道计算方法存在计算量大、改变雅可比能量和局限于计算特定周期轨道等不足,本文提出了一种计算周期轨道的新方法。首先建立了一种初始点和投影点关系的改进型庞加莱截面图,能够更直观地反映随着初始点改变周期轨道的演变和分叉;其次基于改进的庞加莱截面图,通过初始点与投影点的对应关系筛选出可能存在周期轨道的候选区间;然后在该候选区间内利用状态转移矩阵给出距离周期轨道初始点真实解非常接近的初始猜想;最后采用打靶法求解能够快速得到周期轨道的数值解。本文方法不需要改变三体系统的雅可比能量,迭代次数少,能够快速计算得到大范围、具有x轴对称性的周期轨道。以地月圆形限制性三体问题为例进行仿真,验证了该方法的快速性和有效性。
圆形限制性三体问题,周期轨道,庞加莱映射,雅可比能量
0 引 言
周期轨道是深入认识三体问题的关键。随着空间科学技术的不断进步,周期轨道在天体观测、低能轨道转移、天体间循环轨道等方面得到了越来越多的发展,为星际探测、资源开发、载人工程等方面提供了有效的解决方案,探索周期轨道也成为进一步探索其他复杂类型轨道的基础。因此研究周期轨道的计算方法在深空探测中具有重要的意义。
周期轨道通常是通过大范围遍历搜索方法计算得到,这种方法耗时过长,为此很多学者开展了大量的研究,以求得到更有效的周期轨道求解方法。美国学者Richardson[1]提出三阶解析解来获取平动点周期轨道,但其精度无法满足实际任务的要求;Breakwell等[2]通过打靶法对近似解反复迭代计算出较精确的平动点周期轨道数值解,这种方法需要同时积分包含42个方程的微分方程组而得到状态转移矩阵,计算量较大;希腊学者Antoniadou等[3]通过周期轨道的分叉和连续找到给定周期轨道附近的一系列周期轨道,这种方法需要给定初始参考轨道,对于周期轨道的全局搜索具有局限性;Russell[4]将打靶法和方格搜索相结合得到全局范围内符合精度的周期轨道数值解;Anderson等[5]应用Russell方法搜索了一系列不稳定周期轨道,但是这种方法会改变三体系统的雅可比能量值;印度学者Dutt等[6]通过观察庞加莱截面图中轨道流形形成的KAM[7]环的圆心,通过圆心位置与雅可比(Jacobi)能量的对应关系给出了一组周期轨道在不同雅可比能量下的发展趋势;巴西学者Winte等[8]用同样的方法得到了绕月周期轨道随着雅克比能量变化的趋势图。在传统的庞加莱截面图中,轨道流形需要通过多次投影才能形成KAM环;另外仅从庞加莱截面图上观察不能确定轨道与其投影点的对应关系,而且只能找到稳定周期轨道,不稳定周期轨道由于不存在岛屿的吸引,不能在庞加莱截面图上找到。
国内也有不少学者对三体问题的周期解开展了长期而深入的研究。南京大学的刘林等[9],侯锡云等[10],北京航空航天大学的徐明等[11],北京理工大学的崔平远[12]围绕着平动点周期轨道进行了大量的研究;哈尔滨工业大学的张振江等[13]提出一种基于三阶解析解的平动点周期轨道确定算法;国防科学技术大学的连一君[14]对平动点附近周期轨道的迭代初值的获取进行了研究;罗宗富等[15]基于迭代算法求解Backflip型周期轨道;北京理工大学的张文博等[16]针对地月系统中循环往返于地球和月球之间的地月系统周期轨道进行了建模和计算研究;Shang等[17]利用方格搜索方法进行了周期轨道的全局搜索;西北工业大学的张汉清等[18]通过构造一类流函数对初始值进行逐步积分得到与x轴相交指定次数的周期轨道数值算法,这种方法只能得到某一指定与x轴相交次数的周期轨道,而且对初始状态逐步数值积分的方法具有遍历性,计算量过大。
目前现有的周期轨道计算方法大多针对特定类型的周期轨道而完成[1-3,9-16];而全局周期轨道计算方法主要有流函数法[18],打靶法和方格搜索结合的方法[4-5,17],庞加莱截面法[6,8]。流函数法建立在大范围遍历搜索基础上,存在计算量过大的缺点。将打靶法和方格搜索相结合能够在一定程度上减少遍历搜索计算量过大的问题,但是这种方法需要改变三体系统的雅可比能量值。庞加莱截面法能够在特定雅可比能量下,通过观察庞加莱截面图中轨道流形形成的KAM环的圆心来确定周期轨道,但是通过这种方法只能得到稳定周期轨道。
针对现有周期轨道数值算法所存在的计算量大、需改变雅可比能量及局限于计算特定周期轨道等方面的不足,本文提出一种新的方法来实现周期轨道的快速计算。首先建立能够清晰描述初始点与投影点的对应关系的改进庞加莱截面图,提出周期轨道区间的筛选方法和初始点猜想生成策略;其次在此基础上快速完成周期轨道初始点的数值求解;最后以地月系统圆型限制性三体问题为例,对本文方法进行了验证,并通过周期轨道在改进庞加莱截面图上的对应关系从稳定性角度对周期轨道进行了分析和总结。
1 平面圆形限制性三体问题
1.1 动力学模型
(1)
式中:Ω为旋转坐标系下的等效势能:
(2)
式中:μ为两主天体的质量比常数,设矢量r1,r2为探测器到两个主天体的距离,有:
(3)
CRTBP系统中,存在雅可比积分如下:
(4)
可以发现,平面CRTBP系统具有沿x轴的对称性,满足如下转换关系:
(5)
1.2 庞加莱映射和周期轨道
庞加莱映射是在CRTBP的研究中经常用到的一个基本工具[22],其基本原理是将n维流形投影到n-1维的截面上,能以n-1维离散系统来代替n维连续系统的流,这个截面叫做庞加莱截面。在平面CRTBP中,一般以一维x坐标轴,即y=0作为二维轨道的庞加莱截面,方向定义为y>0的方向。如果一个轨道的流形在庞加莱截面上的投影为有限点,则这个轨道为周期轨道,所投影的点是周期点,周期轨道在周期T内满足:
(6)
周期轨道如果在周期T内上穿x轴N次,则为N-周期轨道。
通过庞加莱截面来搜索周期轨道时流形的初始状态通常由式(7)得出:
(7)
由于平面CRTBP系统具有沿x轴的对称性,则搜索出的周期轨道也沿x轴对称,而t=0时周期轨道在庞加莱截面上的投影点为周期轨道初始点。
1.3 周期轨道稳定性判据
稳定周期轨道吸引或者束缚附近的轨道,对周围的流形长时间捕获,周围存在以其周期点为中心的连续的拟周期轨道,而不稳定周期轨道对附近的流形没有吸引作用,周围不存在以其周期点为中心的连续的拟周期轨道。
周期轨道的稳定性通常由状态转移矩阵判断,周期轨道附近的流形可以通过如下线性方程得到:
(8)
定义稳定性判据:
(9)
2 基于改进庞加莱截面图的周期轨道数值算法
本文建立了一种改进的庞加莱截面图,利用改进庞加莱截面图能够记录初始点与其投影点对应关系的特点筛选出周期轨道的候选区间,利用状态转移矩阵的理论计算出距离周期轨道初始点非常接近的初始猜想值,根据周期轨道一个周期内初始点和终点的误差来调整猜想值,通过打靶法得出精度较高的周期轨道数值解。
2.1 改进庞加莱截面图
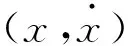
在平面CRTBP系统中,给定雅可比能量,在x轴上均匀选取一系列等间隔的点作为轨道流形的初始位置,以垂直于x轴的速度作为初始速度,则流形初始状态由式(7)得出。如果相邻初始点第N次在庞加莱截面图上的投影的连线与状态分界线x=x0相交,则在该区间内可能存在N-周期轨道初始点。图1为以地月系统(μ=0.01215,C=3.18)为例的改进庞加莱截面图,在区间[0,1]内取间隔为0.01的初始点,首次上穿x轴时的投影用红色圆点标出,通过这些投影点的连线,可知区间(a,b),(c,d),(e,f),(g,h),(i,j)中可能存在1-周期轨道初始点。
本文研究发现,初始点搜索间隔由所搜索的周期轨道的周期数N决定。当N较小时,可以选择相对较小的间隔点;而当N较大时,由于轨道相流结构的复杂性,在很小的间隔内可能存在数个周期轨道,所以需要选择较小的间隔才能保证尽可能得到所有的周期轨道初始点。
2.2 周期轨道数值解法
由于CRTBP对计算初值非常敏感,初始猜想值直接决定了打靶法的迭代次数。本文利用状态转移矩阵的理论在经筛选的周期轨道区间内,计算出周期轨道初始点的猜想值,由于猜想值与周期轨道初始点数值上非常接近,所以只需经过很少的迭代次数,就能够通过打靶法得出精度较高的周期轨道数值解。
(10)
(11)
写成如下形式的方程组:
(12)
(13)
进而可得:
(14)
可得出m11,m14的值,再由式(15) 得到初始猜想x0的数值解:
(15)
当x0不满足精度时,设x为周期轨道在x轴上的初始位置,则周期轨道的最终位置仍旧是x,可以根据式(16)迭代逼近得出周期轨道初始点的解:
(16)
式中:xinitial,xN_initial,xfinal,xN_final分别为前两步打靶得到的猜想周期轨道在一个周期内的初始点和终点(首次迭代时选择候选区间中点x2和初始猜想值x0为前两步猜想周期轨道初始点),x为调整后的周期轨道初始点,在迭代过程中根据式(11)不断缩小周期轨道区间,直到得到符合精度的数值解为止。迭代过程中当猜想值不在可能区间内时,方法失效,这种情况下可以认为是所选定区间内不存在周期轨道初始点。图1中的筛选出的五个候选区间有四个区间内存在周期轨道,图2 (a) , 图2 (b), 图2 (c), 图2(d)分别为初始点在图1中区间(a,b),(c,d),(e,f), (i,j)内的1-周期轨道,其中图2(b)为李亚普诺夫(Lyapunov)轨道,而区间(g,h)内不存在周期轨道初始点。
3 数值验证
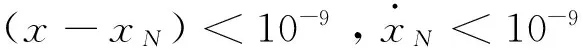
3.1 周期轨道计算
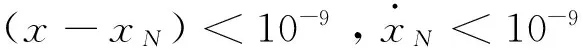
图3为轨道上穿x轴20次的所有投影点所组成的改进庞加莱截面图,其中稳定周期轨道的投影点用红色圆圈表示,不稳定周期轨道的投影点用绿色‘*’表示。图4为图3中稳定周期轨道的流形图,图4(a), 4(b), 4(c), 4(d), 4(e), 4(f), 4(g), 4(h) , 4(i), 4(j), 4(k), 4(l), 4(m), 4(n), 4(o) , 4(p), 4(q), 4(r), 4(s)分别与图3中的稳定周期轨道a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s相对应。稳定周期轨道的初始位置和上穿x轴的次数在表1中列出,其中N表示上穿次数,x0表示初始位置。通过图3和图4可以看出稳定周期轨道随着初始点改变轨道流形演变的趋势和的分叉情况,如稳定周期轨道c,g,n可以被认为是产生分叉的参考轨道,其周围存在一些形状相似,周期数更多的周期轨道族;而不稳定周期轨道不存在这种规律。在固定雅可比能量下,随着x轴上初始值的增大,周期轨道流形的形状从远离地球再回到地球附近的一个过程中,轨迹流形从存在交叉点到弧形逐渐变得平滑。
由于周期轨道沿x轴对称,在一个周期内,当轨道垂直上穿x轴时,在改进庞加莱截面图上投影一次,而当轨道非垂直上穿x轴时,在改进庞加莱截面图的同一个投影点上完成两次投影。周期轨道的周期数N与其在改进庞加莱截面图上的投影点具有如下对应关系:
N=2NNO+NO
(17)
式中:NO代表周期轨道垂直上穿x轴的次数,可以为一次或两次,NNO为周期轨道非垂直上穿x轴的次数,可以为任意次数。
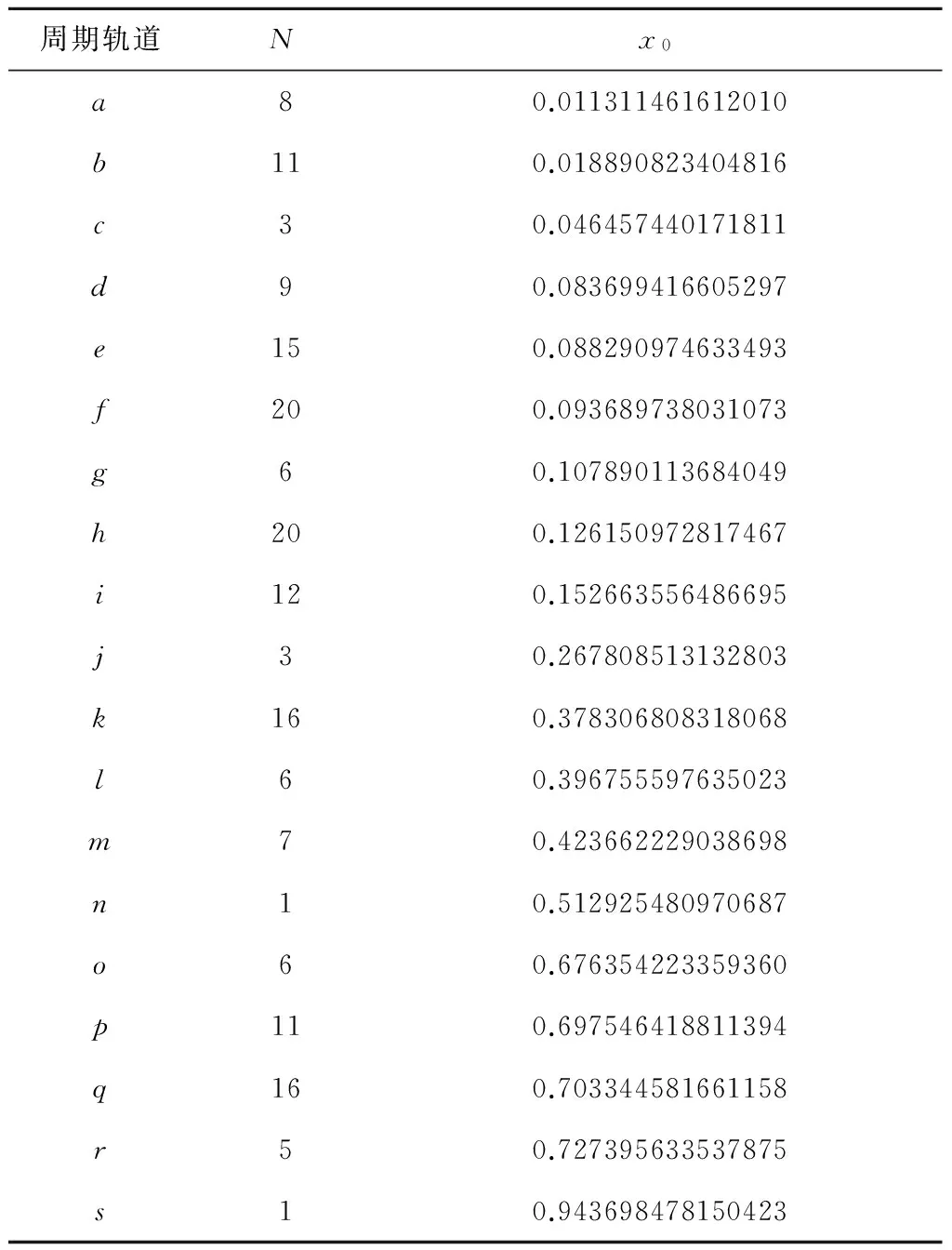
表1 图4中对应的N-周期轨道初始位置Table 1 Initial position of periodic orbits in Fig.4
本文研究发现,周期轨道搜索的有效性与搜索时的采样区间有直接关系。稳定周期轨道由于其对周围轨道的吸引,容易被搜索到;不稳定周期轨道对其周围轨道没有吸引,具有不确定性。不稳定周期轨道的搜索与间隔点的选择有直接关系,而当周期轨道上穿x轴次数越多时其轨道流形可能具有越复杂的结构,所需选择的间隔点距离越小,也可以认为除了遍历搜索外任何方法不能保证得到全部周期轨道。
3.2 改进庞加莱截面图及周期轨道分析
如图3所示,不同初始点在系统中表现了不同的状态,在改进庞加莱截面图上投影有限点所对应的初始点为周期轨道点,周围的规则区域为拟周期轨道区域,投影点散乱的区域为混沌区域。稳定周期轨道由于对周围流形的吸引,周围存在拟周期轨道。
周期数较少的周期轨道周围的拟周期轨道中可能存在新的周期数较多的周期轨道。在改进庞加莱界面图中,一些稳定周期轨道和不稳定周期轨道同处于某一拟周期轨道区域内,具有相似的流形结构,位置相近,不易被区分。图3中的不稳定周期轨道t和稳定周期轨道o均位于稳定周期轨道n的拟周期轨道区域内,而通过稳定性判据可以判断其稳定性,将庞加莱截面图放大,也可以看出不同。图5(c)对应图3中的稳定周期轨道o,图5 (b)为拟周期轨道w,图5(a)对应图3中的不稳定周期轨道t, 图5(d)为它们在庞加莱截面图上相应的投影点。图5 (a)、(b)、(c)均存在于庞加莱截面图的KAM环形岛屿中,即都存在于某周期轨道的拟周期范围内。在庞加莱截面图5(d)上,以点t、o为初始点的轨道在庞加莱截面图上投影为有限点,以点w为初始点的轨道在庞加莱截面图上投影为无限个点,所以以点t、o为初始点的轨道为周期轨道,以点w为初始点的轨道为拟周期轨道。其中,点o周围有自己的KAM环结构,o位于中心,所以o是稳定周期轨道,而t为拟周期轨道中存在的不稳定周期轨道。通过特征值和稳定性判据也可以对周期轨道的稳定性进行验证。
在投影点散乱的混沌区域内,探测器通过初始点是否能够在没有能量消耗的情况下滑行到月球附近可以通过改进庞加莱截面图反映出。图3中,当初始点靠近地球,而投影点出现在月球附近时,代表探测器从靠近地球的一边出发,在上穿x轴20次内可以进入月球区域。而满足条件的不稳定周期轨道在绕月球旋转几周后返回地球区域完成天体间转移[25],在地月低能转移轨道的应用中具有重要的参考价值。图6为本文算法搜索到的初始点靠近地球的地月转移周期轨道,其中,左边红色圆点代表地球,右边红色圆点代表月球,黑色圆环代表每个周期轨道的初始位置x0。
4 结 论
本文建立了一种基于改进庞加莱截面图计算CRTBP问题周期轨道的快速数值求解方法。该方法在不改变雅可比能量的基础上,不需要过多的投影次数,大范围搜索出与上穿x轴给定次数内的周期轨道,算法迭代次数少,具有广泛的应用价值。由于CRTBP的对称性,本文方法所选轨道初值只适用于对称周期轨道的搜索,得到的周期轨道与采样间隔有直接关系,而不稳定周期轨道及其周围的流形具有复杂的结构,尤其当轨道上穿x轴次数越多时,两周期轨道之间的间隔可能越小,所以采样间隔的选取是周期轨道的搜索过程中需要考虑的重要问题。由于本文提出计算周期轨道的方法是基于周期轨道的定义而建立的,并不局限于限制性三体问题下,对于非线性动力学系统具有普遍的适用性。
[1]RichardsonDL.Analyticconstructionofperiodicorbitsaboutthecollinearpoint[J].CelestialMechanics&DynamicalAstronomy, 1980, 22(3):241-253.
[2]BreakwellJV,BrownJV.The‘Halo’familyof3-dimensionalperiodicorbitsintheEarth-Moonrestricted3-bodyproblem[J].CelestialMechanicsandDynamicalAstronomy, 1979, 20(4):389-404.
[3]AntoniadouKI,VoyatzisG,KotoulasT.Onthebifurcationandcontinuationofperiodicorbitsinthethreebodyproblem[J]. 2010, 21(8):2211-2219.
[4]RussellRP.Globalsearchforplanarandthree-dimensionalperiodicorbitsnearEuropa[J].TheJournaloftheAstronauticalSciences, 2006, 54(2):199-226.
[5]AndersonRL,CampagnolaS,LantoineG.Broadsearchforunstableresonantorbitsintheplanarcircularrestrictedthree-bodyproblem[J].CelestialMechanicsandDynamicalAstronomy, 2016, 124(2): 177-199.
[6]DuttP,SharmaRK.EvolutionofperiodicorbitsneartheLagrangianpointL2[J].AdvancesinSpaceResearch, 2011, 47(11):1894-1904.
[7]OliveiraHPD,SoaresID,ToniniEV.NonlinearresonanceofKolmogorov-Arnold-Mosertoriinbouncinguniverses[J].JournalofCosmology&AstroparticlePhysics, 2006, 2(2):76-80.
[8]WinterOC,VieiraNetoE.Distantstabledirectorbitsaroundthemoon[J].Astronomy&Astrophysics, 2002, 393(2):661-671.
[9] 刘林, 侯锡云, 王海红. 关于共线平动点的特征在深空探测中的应用[C]. 中国宇航学会首届学术年会,哈尔滨,2005年1月12-14日. [LiuLin,HouXi-yun,WangHai-hong.OnapplicationofCollinearLibrationpointsindeepspaceexploration[C].TheFirstAcademicyearattheChineseAcademyofSpace,Harbin,January12-14, 2005.]
[10] 侯锡云, 刘林. 利用太阳帆定点探测器在地—月系共线平动点附近的探讨[J]. 宇航学报, 2009, 30(6):2249-2257. [HouXi-yun,LiuLin.Onorbitcontrolofspacecraftswithsolarsailaroundtheearth-mooncollinearlibrationpoint[J].JournalofAstronautics, 2009, 30(6):2249-2257.]
[11] 徐明, 徐世杰.Halo轨道维持的线性周期控制策略[J]. 航天控制, 2008, 26(3):13-18. [XuMing,XuShi-jie.Stationkeepingstrategyofhaloinlinearperiodiccontrol[J].AerospaceControl, 2008, 26(3): 13-18.]
[12] 崔平远. 深空探测轨道设计与优化[M]. 科学出版社, 2013.
[13] 张振江, 崔枯涛, 崔平远. 基于三阶解析解的小行星平衡点附近halo轨道确定方法研究[J]. 宇航学报, 2011, 32(2):277-283. [ZhangZhen-jiang,CuiHu-tao,CuiPing-yuan.Researchonthird-orderayalyticalsolutiondeterminationofhaloorbitsaroundequilibriumpointofasteroid[J].JournalofAstronautics, 2011, 32(2):277-283.]
[14] 连一君. 基于三体平动点的低能转移轨道设计研究[D]. 长沙:国防科学技术大学, 2008. [LianYi-jun.Researchonlow-costtransfertrajectorydesignbasedonthree-bodylibrationpoints[D].Changsha:NationalUniversityofDefenseTechnology, 2008.]
[15] 罗宗富, 孟云鹤, 汤国建. 双月旁转向轨道的动力学与建模研究[J]. 宇航学报, 2012, 33(10):1361-1369. [LuoZong-fu,MengYun-he,TangGuo-jian.Dynamicsandmodelingofdoublelunar-swingbytrajectories[J].JournalofAstronautics, 2012, 33(10):1361-1369.]
[16] 张文博, 成跃, 王宁飞. 地月循环轨道动力学建模与计算研究[J]. 宇航学报, 2015, 36(5):510-517. [ZhangWen-bo,Cheng-Yue,WangNing-fei.Dynamicsmodelingandcalculationofcyclertrajectoriesintheearth-moonsystem[J].JournalofAstronautics, 2015, 36(5):510-517.]
[17]ShangH,WuX,CuiP.Periodicorbitsinthedoublysynchronousbinaryasteroidsystemsandtheirapplicationsinspacemissions[J].Astrophysics&SpaceScience, 2015, 355(1):69-87.
[18] 张汉清, 李言俊, 张科. 一种计算圆形限制性三体问题周期轨道的新方法[J]. 中国科学:技术科学, 2011, 41(8):1078-1083. [ZhangHan-qing,LiYan-jun,ZhangKe.Anovelmethodofperiodicorbitcomputationincircularrestrictedthree-bodyproblem[J].ScientiaSinicaTechologica, 2011, 41(8): 1078-1083.]
[19]SzebehelyV,JefferysWH.Theoryoforbits:therestrictedproblemofthreebodies[J].AmericanJournalofPhysics, 1968, 36(4):375.
[20]KoonWS,LoMW,MarsdenJE,etal.Dynamicalsystems,thethree-bodyproblemandspacemissiondesign[M].NewYork:Springer-Verlag, 2007.
[21] 刘林. 航天器轨道理论[M]. 国防工业出版社, 2000.
[22]JungC.Poincaremapforscatteringstates[J].JournalofPhysicsAGeneralPhysics, 1998, 19(8):1345-1353.
[23]BosanacN,HowellKC,FischbachE.Stabilityoforbitsnearlargemassratiobinarysystems[J].CelestialMechanics&DynamicalAstronomy, 2015, 122(1):27-52.
[24]BosanacN,HowellKC,FischbachE.Anaturalautonomousforceaddedintherestrictedproblemandexploredviastabilityanalysisanddiscretevariationalmechanics[J].Astrophysics&SpaceScience, 2016, 361(2):1-18.
[25]LeivaAM,BriozzoCB.ControlofchaosandfastperiodictransferorbitsintheEarth-MoonCR3BP[J].ActaAstronautica, 2006, 58(8):379-386.
通信地址:西安市友谊西路127号西北工业大学航天学院(710072)
电话:(029)88492788
E-mail:zhengyue-nwpu@qq.com
(编辑:张宇平)
A Novel Method of Periodic Orbit Computation for Three-Body Problem
ZHENG Yue1,2, PAN Bin-feng1,2,3, TANG Shuo1,2,3
(1. College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;2. Shanxi Aerospace Flight Vehicle Design Key Laboratory, Xi’an 710072, China;3. National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China)
Current methods of the periodic orbit computation have the disadvantages of requiring large amount of computation, varying the Jacobi energy, and the limitation to calculate the specific periodic orbits, a novel method of the periodic orbit computation is proposed in this paper. Firstly, a modified Poincaré section map is created, on which the projection points from every initial point are plotted and the evolution and fork of the periodic orbits by the initial point could be intuitively reflected. Secondly, based on the modified Poincaré section map, the candidate interval of the periodic orbits are selected by the relationship between the initial points and the projection points. Thirdly, the initial guesses are generated which are quite close to the true solution in the candidate interval computation using the state transition matrix. Finally, the periodic orbits can be rapidly computed numerically by a single shooting method. The proposed method does not need to change the Jacobi energy, requires less iterations for a given value of the Jacobi energy, and enables a large set of periodic orbits withx-axis symmetry. Examples are presented in the Earth-Moon Circular Restricted Three-Body Problem to verify the efficiency and rapidity of this method.
Circular restricted three-body problem; Periodic orbit; Poincaré section; Jacobi energy
2016-11-05;
2017-02-24
国家自然科学基金(11672234)
V
A
1000-1328(2017)04-0384-09
10.3873/j.issn.1000-1328.2017.04.008
郑 越(1983-),女,博士生,主要从事深空探测、轨道设计等研究。
