基于MATLAB软件的周期符号纠缠函数构造的新混沌系统动力学分析
2017-05-17罗宏伟张建刚杜文举安新磊
罗宏伟++张建刚++杜文举++安新磊++卢加荣

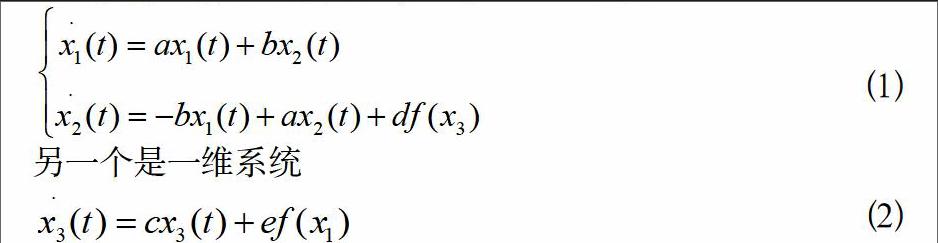
摘要:使用周期符号函数对两个稳定的子系统进行纠缠,构造了一个新三维混沌控制系统,理论分析了新三维控制系统的耗散性、有界性、平衡点的稳定性和Hopf分岔的条件,通过计算得到了系统在平衡点的第一Lyapunov指数,进一步分析了分岔的方向和稳定性。通过MATLAB软件,对系统进行数值模拟,验证了理论分析的正确性。
关键词:纠缠函数;混沌;Hopf分岔;平衡点;Lyapunov 指数
中图分类号:O415.5 文献标识码:A 文章编号:1007-9416(2017)03-0054-04
混沌现象的特征即蝴蝶效应,具有对初值敏感而表现出的不可预测的、类似随机性的运动。自Lorenz [1]在三维自治系统中发现混沌吸引子以来,在过去数十年中,随着科学技术的发展和进步,混沌理论得到了空前发展,尤其在数学、物理及其工程实际应用中得到极大发展,关于混沌的构造和分析方法已经成为最新的研究热点问题[2,4,5,6]。文献 [7]通过构造了一个新的混沌,文献[8,9,10]利用分段技术,发现了一些新的混沌吸引子的存在,文献[11]首次提出纠缠函数的基本概念,并给出构造混沌的基本原理,即使用纠缠函数通过对两个或更多的线性稳定子系统进行纠缠,可产生混沌系统。构造人工混沌在解决噪声污染,提高天气预测的准确度,保持非线性机械系统稳定性等方面有重要意义。
本文使用周期符号函数作为纠缠函数,对两个线性子系统进行纠缠,构造出了一个新的三维混沌系统,通过对系统的耗散性、有界性、平衡点稳定性、Hopf分岔和Lyapunov指数等动力学特性进行了分析,最后通過数值模拟验证理论的结果。
1 系统描述
考虑两个线性子系统,其中一个是二维系统
另一个是一维系统
其中是状态变量,当和,系统(1)和(2)是稳定的,用周期符号函数纠缠以上两个子系统,可得如下三维控制系统:
3 数值仿真
根据引理1和定理2,当,,和时,平衡点是渐进稳定的。
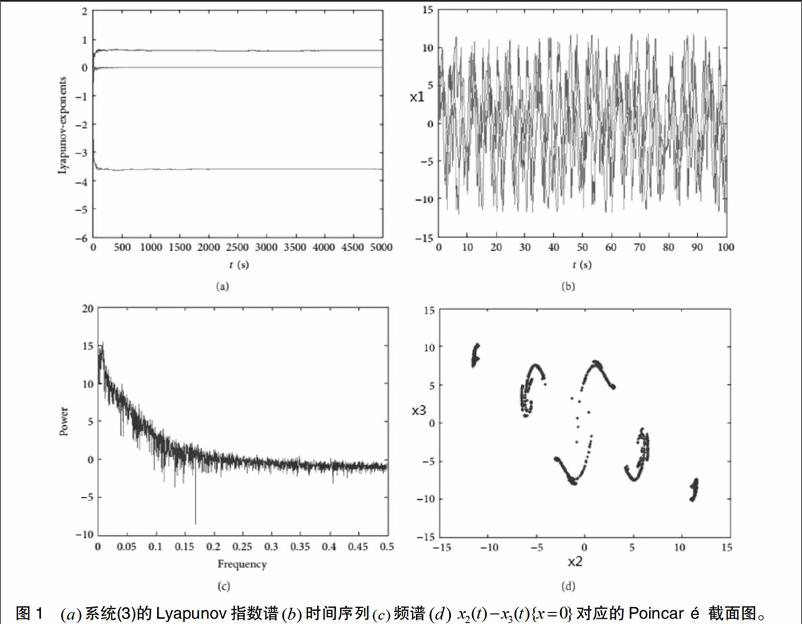
系统(3)的Lyapunov 指数可以通过文献[15]提供的方法计算得到,其中Lyapunov 指数,and如图1所示,时间序列、频谱和Poincaré 截面图分别如图1所示。当和,出现混沌纠缠现象,其三维相图,和二维相图分别如图2所示。 当参数和值不变,作为变量时,系统(3)的动力行为如图3所示。
4 结语
本文将一个周期符号函数作为纠缠函数,利用混沌纠缠的基本原理,对两个稳定子系统进行纠缠,人工构造出一个新三维控制系统,根据混沌系统的分析方法,对新三维控制系统的动力学特性进行了理论分析,结果发现新构造的系统具有混沌的特征,并使用MATLAB软件进行了数值模拟,验证了理论分析的结果。该方法为我们解决工程中混沌问题提出来新的思路。
参考文献
[1]E.N.Lorenz,“Deterministic nonperiodic flow,”Journal of the Atmospheric Sciences, vol.20, :130-141,1963.
[2]Pecora L M, Carroll T L.Synchronization in chaotic systems.[J]. Physical Review Letters, 1990,64(8):821-824.
[3]Chu Y D, Li X F, Zhang J G, et al。 Nonlinear dynamics analysis of a new autonomous chaotic system[J]. Journal of Zhejiang University-SCIENCE A, 2007, 8(9):1408-1413.
[4]李险峰,张建刚,禇衍东.一个新自治混沌系统的动力学分析[J].复杂系统与复杂性科学,2008,5(1):28-36.
[5]杜文举,俞建宁,张建刚,等.一个新混沌系统的Hopf分岔分析及其电路实现[J].四川大学学报自然科学版,2013,50(5):1025-1031.
[6]李群宏,徐德贵.一个类Lorenz系统的动力学分析[J].重庆理工大学学报自然科学版,2011,25(2):112-116.
[7]Tang K S, Man K F, Zhong G Q, et al. Generating chaos via x|x|[J].IEEE Transactions on Circuits & Systems I Fundamental Theory & Applications, 2001, 48(5):636-641.
[8]Jinhu Lü,Guanrong Chen.A new chaotic attractor coined[J].International Journal of Bifurcation & Chaos,2002,12(3):659-661.
[9]Liu X, Teo K L, Zhang H, et al. Switching control of linear systems for generating chaos ☆[J]. Chaos Solitons & Fractals, 2006,30(3):725-733.
[10]Liu C, Liu T,Liu L,et al.A new chaotic attractor[J].Chaos Solitons & Fractals, 2004, 22(5):1031-1038.
[11]Hongtao Zhang,Xinzhi Liu,Xuemin Shen,et al.Chaos entanglement:A new approach to generate chaos[J].International Journal of Bifurcation & Chaos,2013,23(05):30014.
[12]Celikovsky S,Chen G.On the generalized Lorenz canonical form ☆[J].Chaos Solitons & Fractals,2005,26(5):1271-1276.
[13]Dias F S, Mello L F, Zhang J G.Nonlinear analysis in a Lorenz-like system[J].Nonlinear Analysis Real World Applications,2010,11(5):3491-3500.
[14]Moussi E H, Bellizzi S, Cochelin B, et al.Nonlinear normal modes of a two degrees-of-freedom piecewise linear system[J]. Mechanical Systems & Signal Processing, 2015,64:266–281.
[15]Wolf A, Swift J B, Swinney H L,et al.Determining Lyapunov exponents from a time series[J].Physica D Nonlinear Phenomena, 1985, 16(3):285-317.
