一种均衡考虑锂电池内部能量损耗和充电速度的多段恒流充电方法

刘 伟 吴海桑 何志超 孙孝峰 杨 耕

(1.沧州师范学院机械与电气工程学院 沧州 061001 2. 清华大学自动化系 北京 100084 3.燕山大学电力电子节能与传动控制河北省重点实验室 秦皇岛 066004)



一种均衡考虑锂电池内部能量损耗和充电速度的多段恒流充电方法

刘 伟1吴海桑2何志超2孙孝峰3杨 耕2

(1.沧州师范学院机械与电气工程学院 沧州 061001 2. 清华大学自动化系 北京 100084 3.燕山大学电力电子节能与传动控制河北省重点实验室 秦皇岛 066004)

锂电池快速充电方法应该均衡考虑电池的安全、寿命和充电时间。为此，应该控制锂电池的温度或能量损耗。提出一种均衡考虑锂电池能量损耗和充电时间的多段恒电流充电方法。首先，通过测试不同电流的恒流工况充电电压曲线，建立锂电池直流内阻随荷电状态(SOC)和电流I变化的函数关系式。其次，简化恒流段内能量损耗计算表达式，并设计用于均衡充电时间和能量损耗的充电目标方程。最后，设计一条权重变化曲线以确定各个恒流段的充电电流。此方法实验过程简单，充电电流的计算过程简单。通过与恒流充电方法的实验比较，验证了该方法的优点。

锂电池直流内阻 充电时间 能量损耗 恒流充电 权重

0 引言

锂电池具有功率密度高、能量密度高、工作温度范围宽、寿命长、无记忆效应、自放电率低等优点，是未来电动汽车动力电池的主要发展趋势[1,2]。锂电池使用过程中，温度是影响其寿命和安全性的主要影响因素之一。在一定温度范围内，锂电池温度越高，寿命衰减越快[3-5]。由于发生在锂电池直流内阻上的能量损耗是锂电池温升的主要热源，所以充电电流对锂电池性能和寿命的影响较大[6,7]。

虽然传统的恒流快速充电方法能够减少充电时间，但会造成锂电池的能量损耗大、温升大、端电压高、寿命短等不利影响[8]。多段恒流充电方法被认为是一种改进的工程性充电方法，其主要优点包括延长电池寿命、提高电池充放电效率、缩短充电时间等[9,10]。目前，多段恒流充电方法的恒流分段数量并没有准确的依据，一般分为4～5段，且优化目标各有不同。文献[11-13]采用全局优化算法计算各段的优化电流，例如遗传算法(Genetic Algorithm，GA)、蚁群算法(Ant Colony Algorithm，ACA)、粒子流算法(Particle Swarm Optimization Algorithm，PSOA)等。文献[14,15]采用塔古奇方法，应用正交矩阵方法设计了若干组实验，根据实验数据搜索最优的充电模式。综上所述，已有的多段恒流充电方法是基于大量的实验数据，且寻优方法比较复杂，不便于实际应用。

为了改善这些问题，并综合考虑锂电池寿命和充电时间，本文提出一种均衡考虑锂电池内部能量损耗和充电速度的多段恒流充电方法，通过控制能量损耗，间接控制对锂电池寿命的影响。相比已有的优化充电方法，本文提出的充电方法可大大减小所需预做实验量，计算优化充电电流的算法较为简单，并且可根据应用需要灵活控制权重变化规律。首先采用基于恒流外特性和荷电状态(Stage of Charge，SOC)的电池直流内阻测试方法，得到不同电流恒流充电工况下的直流内阻变化曲线，建立锂电池直流内阻随SOC和电流I变化的函数关系式。据此，建立用权重兼顾充电时间和能量损耗的目标方程，并简化能量损耗计算公式。为了易于工程实现，本文提出变权重多段恒流充电方法，该方法根据锂电池极限充电电流曲线设计权重变化曲线，进而得到不同恒流段的优化充电电流。

1 锂电池直流内阻辨识

基于锂电池直流内阻模型，通过分别预做不同电流对应的恒流充电工况实验，采用基于恒流外特性和荷电状态的电池直流内阻测试方法测得特定电流下的直流内阻曲线。据此，采用线性拟合法建立直流内阻关于SOC和电流I变化的函数关系式，并将此式的仿真结果与实验数据进行对比。

1.1 锂电池模型和直流内阻测试

本文方法基于锂电池直流内阻模型，其具体形式如图1所示[16,17]。由于本文将锂电池放在恒温箱中，并且所有实验均在25 ℃温度下进行，所以将由充电电流I引起的较小温升问题划归为电流I的影响中。直流内阻R是随SOC和电流I变化的函数，记作R(SOC,I)，故直流内阻模型满足

U(SOC,I)=Uoc(SOC)+R(SOC,I)I

(1)

式中，Uoc(SOC)为开路电压；U(SOC,I)为锂电池的端电压。

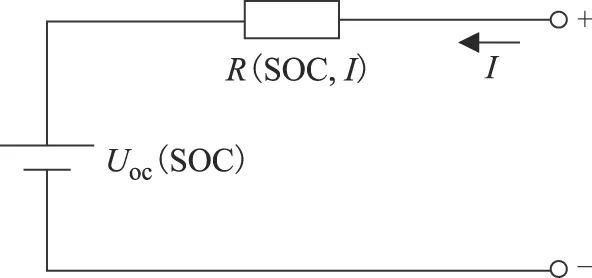
图1 电池直流内阻模型Fig.1 Internal DC resistance battery model

锂电池SOC采用带库伦效率系数的安时积分方法进行计算，即

(2)

式中，SOC(t0)为电池充电初始的荷电状态；t0、tf分别为充电开始和结束时间；η(I)为电流I的库伦效率系数，便于将不同电流计算得到的SOC值与标准电流对应的SOC值进行归一化处理；C为电池容量。

为了解决传统直流内阻测试方法需增加大量实验进行反复测试等问题，文献[17]提出了一种基于恒流外特性和SOC电池直流内阻测试方法，该方法将不同恒流工况下的电池荷电状态变化过程进行归一化处理，从而能够利用恒流充放电端电压曲线来获取不同工作电流及SOC条件下的直流内阻。本文采用此方法进行直流内阻的测试，具体过程由三个步骤组成。

1.1.1 预实验

针对本文所提出的方法，定义：①充电结束的标志是锂电池端电压达到截止电压3.65 V；② 0.2C电流作为充电过程中的标准电流。

在25 ℃室温条件下，分别采用0.2C、0.4C、0.6C、0.8C、1.0C五个电流对锂电池进行恒流充电实验。在计算非标准电流所对应的SOC值时，需要与标准电流进行折算，即求充电电流I对应的库伦效率系数η(I)[15]。

当使用标准电流I0=0.2C电流对锂电池进行充电时，SOC变化范围为0～1.0；采用其他电流I对锂电池进行充电，当锂电池端电压达到3.65 V时，改用I0=0.2C继续对锂电池进行充电，端电压再次达到3.65 V，认为此时电池SOC近似为1.0，本文将这种充电过程记作I&I0。所有实验均使用0.2C电流对锂电池进行放电。实验使用型号为HX1865130AF的磷酸铁锂电池有两种容量，即10 A·h和8.5 A·h，具体参数见表1。

表1 电池规格

不同充电方式的充、放电容量数据见表2，其中Qd为锂电池采用电流I0进行放电的放电容量，QI为在充电过程I&I0中电流I充入的容量，QI0为在充电过程I&I0中电流I0充入的容量。根据表2中数据进行曲线拟合，得到库伦效率系数的计算式为

η(I)=0.106I3-0.232I2+0.171I+0.974

(3)

表2 不同充电方式的充、放电容量数据

1.1.2 直流内阻测试

采用文献[17]中的直流内阻计算方法，由式(2)和式(3)可将不同恒流工况下的电池荷电状态变化过程归一化，然后利用式(1)可近似求得两个工作电流I1和I2的代数平均值(I1+I2)/2对应的直流内阻曲线，如图2所示。直流内阻计算式为

(4)

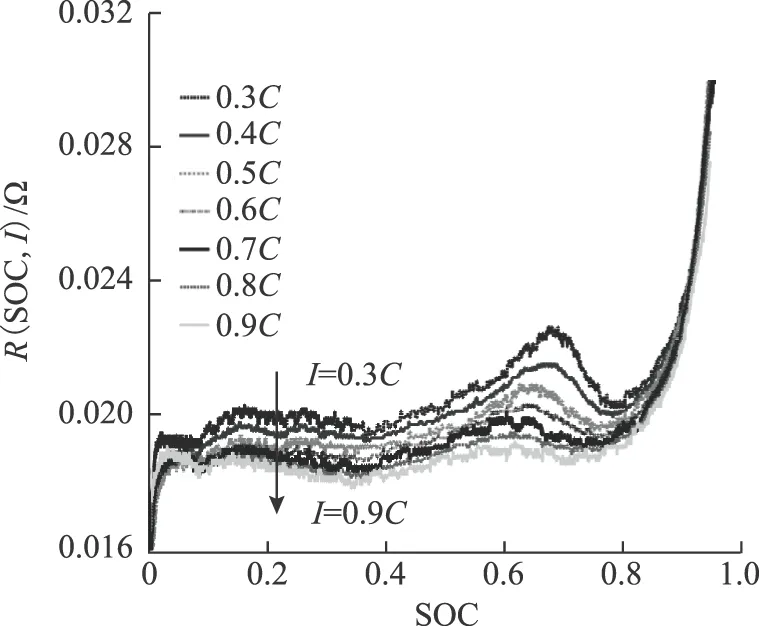
图2 直流内阻变化曲线Fig.2 DC resistance curves

1.1.3 开路电压测试

根据电池的直流内阻模型，使用工作电流I=0.2C电流对电池进行充、放电，由式(1)可得开路电压变化曲线。

1.2 直流内阻函数的辨识

由图2可知，不同电流对应的直流内阻曲线变化趋势相似，且在同一SOC条件下充电电流越大，直流内阻越小。这是因为在锂电池充电过程中，虽然充电电流大小不同，但是锂电池内部物质在相同SOC条件下的化学反应过程类似，仅内部物质的反应速率不同，所以对外表现为锂电池的直流内阻及端电压相似。

不同电流对应的直流内阻曲线变化趋势相近，则选择某一电流对应的直流内阻曲线作为基准曲线，通过作差并求得此直流内阻差值的函数，即可得到不同电流对应的直流内阻增量变化规律。具体步骤如下。

1.2.1 内阻增量随SOC变化曲线

本文选定I1=0.5C对应的直流内阻曲线R1(SOC,I1)作为基准曲线，然后将电流I分别为0.3C、0.4C、0.7C、0.8C、0.9C时对应的直流内阻曲线R(SOC,I)与基准直流内阻曲线作差，在相同SOC条件下两个直流内阻相减，即

ΔR(SOC,I)=R(SOC,I)-R0(SOC,I0)

(5)

根据直流内阻增量的变化曲线，以SOC为自变量对其进行曲线拟合。拟合函数的次数选取得越高，得到的拟合效果越好。本文得到的直流内阻增量变化曲线较为平缓，故采用二次函数对内阻增量曲线进行拟合即可得到较好效果，即

ΔR(SOC,I)=a(I)SOC2+b(I)SOC+c(I)

(6)

1.2.2 直流内阻增量方程系数随电流的变化曲线

基于式(6)对每个电流的直流内阻数据进行拟合处理，可得式(6)中各电流I对应的系数a(I)、b(I)和c(I)，其关系如图3所示。

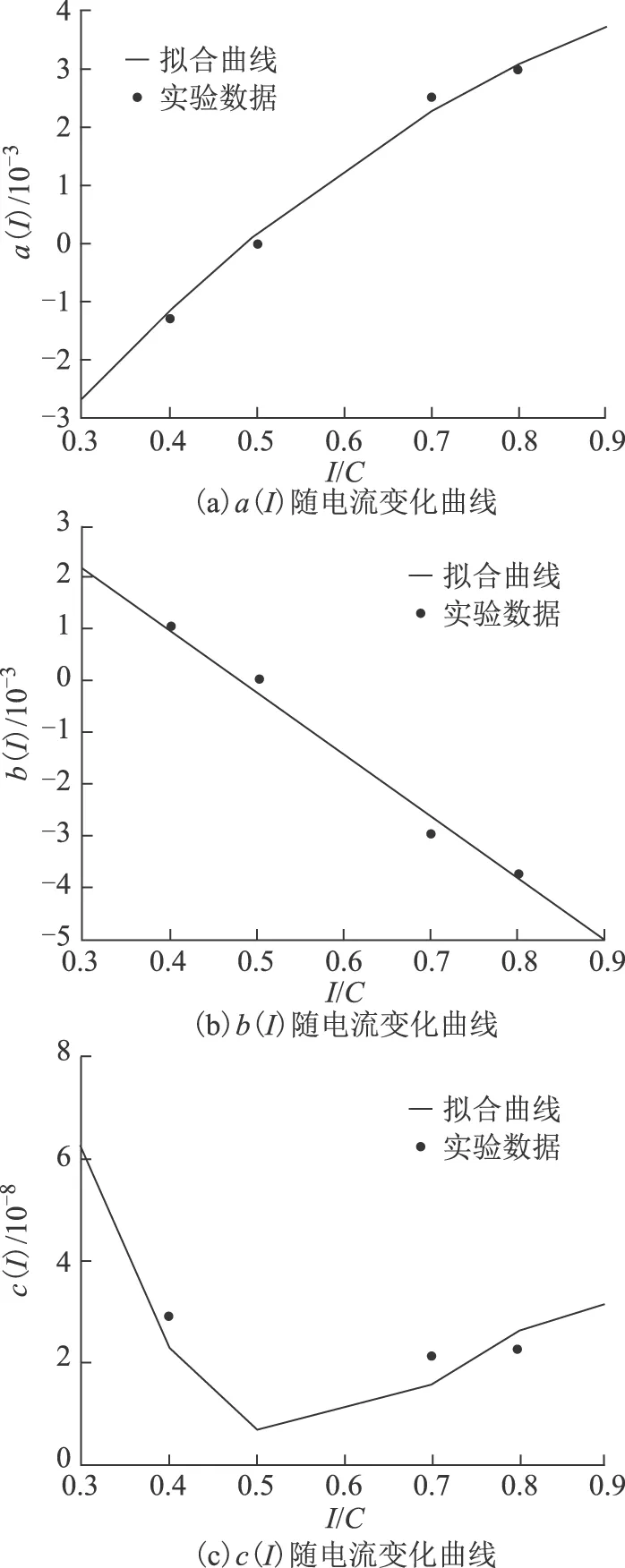
图3 系数随电流变化曲线Fig.3 Coefficient versus current curves

根据系数变化特点，分别采用二次函数、一次函数和三次函数对a(I)、b(I)和c(I) 进行曲线拟合，拟合公式和数值分别为

a(I)=-0.000 084 61I2+0.002 1I-0.008 1

(7)

b(I)=-0.001 2I+0.005 7

(8)

c(I)=-0.000 012I3+0.000 264 5I2-

0.001 8I+0.003 9

(9)

1.2.3 辨识结果与分析

根据以上辨识过程所得到的直流内阻函数，在允许范围内可得到任意充电电流所对应的直流内阻变化曲线。由式(4)可得0.6C电流对应的直流内阻计算数据，并将该数据与以上直流内阻仿真数据对比，说明本文直流内阻辨识的准确性，结果如图4所示。

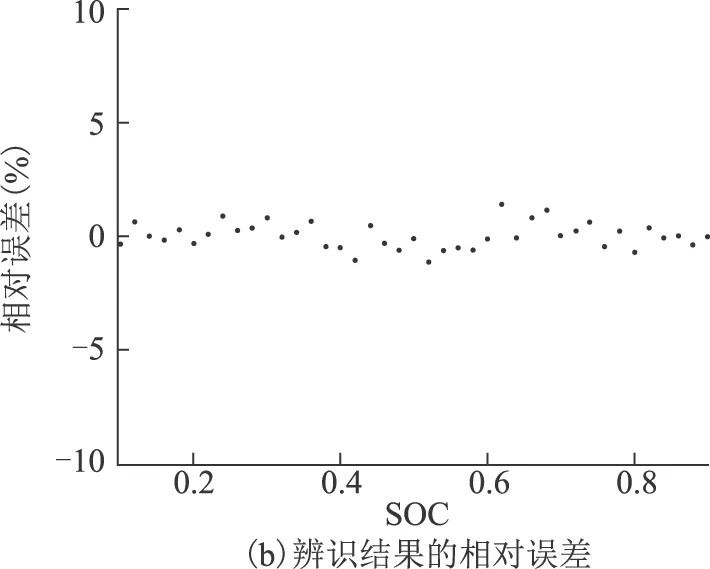
图4 直流内阻辨识效果Fig.4 DC resistance identification

由图4可知，0.6C电流对应的直流内阻相对误差不超过2%，采用这种直流内阻函数辨识方法可得到较为准确的直流内阻曲线。但是，当计算电流与基准曲线电流相差较大时，产生的误差可能会增大。本文通过对不同生产厂商和容量的磷酸铁锂电池分别进行实验，得到结果类似，故可得到初步结论：通过对磷酸铁锂电池在相应条件下进行少量的恒流工况实验，采用此种方法均可求得相应的直流内阻函数关系式，以供优化充电方法或电池管理系统使用。

2 目标方程的建立

在充电过程中，充电能量损耗较低的情况下充电时间越短越好。然而，二者是相互矛盾的，需要建立包含两个目标的关系式。

在SOC尺度下，本文所设计的多段恒流充电方法共分为10段，每个恒流充电阶段的ΔSOC均为0.1。具体分段数并不唯一，可根据需求进行改变。当SOC变化范围为0～0.9时，根据每段的权重值和目标方程计算优化充电电流值；当SOC>0.9时，由于锂电池直流内阻急剧上升，为了减少锂电池发热量，本文选用0.2C电流对锂电池进行充电。

2.1 充电时间与能量损耗

在锂电池充、放电过程中，锂电池内部存在能量损耗，这部分能量损耗是锂电池温度升高的主要原因；随着电流的增大，损耗加剧，温升增加。而温度是影响锂电池寿命和安全性的主要因素之一[5]。在一定温度范围内，锂电池温度越高，寿命衰减越快[3,4]。因此，本文将充电能量损耗作为目标方程中的一个因素。

由式(2)、式(3)可得电流I对应的充电时间t为

(10)

根据欧姆定律及电功计算公式，可得充电过程中的能量损耗为

(11)

当SOC从零开始，分别用0.2C、0.4C、0.6C、0.8C、1.0C的电流充电，所得充电能量损耗如图5所示。

由图5可知，当SOC处于特定变化范围段ΔSOC=0.1时可得Wloss(SOC,I)随电流I的变化曲线。通过对各SOC段内的能量损耗曲线进行以电流I为自变量的曲线拟合，可得各ΔSOC段内的能量损耗简化计算式为

Wloss(SOC(i),I)=k(i)I+g(i)

(12)

式中，Wloss(SOC(i)，I)为电流I在第i个ΔSOC内的损耗，例如，SOC(2)代表SOC变化范围为0.1～0.2；k(i)、g(i)为该SOC(i)段内所对应的方程系数，具体取值见表3。

图5 充电能量损耗曲线Fig.5 Charging energy loss curve

表3 能量损耗公式中系数k(i)和g(i)取值

2.2 目标方程

工程应用中，用户往往希望锂电池能够在较短时间内充入的能量越多越好，并且损耗能量越小越好。能量损耗对锂电池的影响在上文中已进行了初步分析，在此不再赘述。本文设定的目标方程包括充电时间和能量损耗。在SOC段内，目标方程J中所有参数均无量纲，计算式为

J=αMt+(1-α)Wloss(SOC,I)

(13)

式中，t为充电时间；α为时间在目标方程中所占的权重；M为度量常数，为确保两个目标有相同的量级，本文取0.707 2(即当I=0.5C、α=0.5时,使目标方程中两项取值相等得M值)。式(13)右边第一项代表充电时间，第二项代表充电过程的损耗，充电损耗主要发生在直流内阻上。

经过分析，目标方程J只有一个极小值点且为最小值。因此，可通过对式(13)进行求导，并令其等于零，即可得到在电流取值范围内的优化充电电流I。

2.3 充电电流计算结果

当α分别取0.3、0.5、0.7时，通过式(13)得到SOC在0～0.9(ΔSOC为0.1)范围内的优化充电电流，见表4。

表4 不同α值对应的各个SOC(i)段内的充电电流

由表4、图2可知，在权重系数恒定时，每个SOC(i)内，优化充电电流大小的变化趋势与直流内阻变化趋势有关。当直流内阻较大时，计算得到的优化电流较小；当直流内阻较小时，计算得到的优化电流较大。

充电过程，由于锂电池内部反应物质的变化，在不同的恒流充电阶段内，锂电池对充电时间和能量损耗两个因素的敏感程度不同。在不同恒流充电阶段，相同的能量损耗会对锂电池的寿命产生不同的影响。根据锂电池特性，可设计一种能够体现这种敏感程度的方法，即变权重多段恒流充电方法。

3 变权重多段恒流充电方法

锂电池充电过程中，由于其内部化学反应物质的浓度和其他特性会有变化，进而对充电电流的大小需求不同，所以需要动态均衡控制充电能量损耗和充电速度，以满足锂电池的充电特性需求。然而，锂电池直流内阻模型不能全面反映锂电池内部化学反应过程，故权重变化曲线的设计还需借鉴锂电池其他方面的知识。

3.1 锂电池特性分析

锂电池正常充电过程：在充电初期，内部电解质中的锂离子浓度较大，石墨负极板上锂离子与电子结合速度较快，允许用大电流进行充电；随着充电过程的进行，电解质内部锂离子浓度下降，石墨负极板上锂离子与电子结合速度变慢[18],若继续用大电流对锂电池进行充电，在石墨负极上会形成锂金属，当锂金属积累到一定程度时，便会刺穿锂电池的固体电解质界面膜(SEI膜)，从而在电解液中形成锂枝晶[19]。

当锂枝晶过多、充电电流过大时，部分锂枝晶不能完全消失，随后脱离负极并残留在电解液中，进而加速锂电池寿命衰减[19]。随着锂电池充电过程的进行，锂电池可接受的充电电流逐渐递减[20]。

3.2 变权重多段恒流充电方法的实施

锂电池充电过程，需要设计一条合适的权重变化曲线，进而控制充电电流，使得锂电池充电时间短、充入电量多，寿命衰减慢。为了满足锂电池充电特性需求，基于本文目标方程，提出一种变权重多段恒流充电方法。

锂电池端电压是内部物质反应过程的外在表现，极限充电电流曲线可以反映锂电池内部一些特性。据此，本文设计了一条权重变化曲线，用于描述锂电池内部的化学反应特性。

3.2.1 锂电池极限充电电流

定义极限充电电流是在特定SOC条件下，锂电池端电压不超过设定极限值所对应的充电电流值。在此，本文设定的锂电池极限电压为3.65 V，锂电池充电的极限充电电流为

(14)

3.2.2 权重变化曲线设计实例

依据极限充电电流曲线，得到锂电池充电特性的先验知识：在锂电池允许的充电电流变化范围内，充电开始时，锂电池反应物质浓度大，允许采用较大电

流充电，即在充电初期，充电时间的重要性大于能量损耗，即使电池温度上升也不会对寿命造成较大影响；在充电末期，锂电池内部反应物浓度减小，大电流充电会对锂电池寿命造成较大影响，故而能量损耗的重要性较大，应减小电池温度[5,19]。在电池充电初期，温度的适量增加会增加锂电池内部化学物质的活性，促进化学反应的进行，降低锂电池的内阻，这对充电是有利的。

据此，本文设计了一条权重变化曲线，设计过程为：在充电开始时，权重为1；在充电结束时，权重为0；在SOC变化范围为0～1时，将极限电流变化曲线上各点值除以极限电流最大值，从而得到此阶段内的权重变化曲线。综上所述，可得到目标方程中权重的变化曲线，如图6所示。

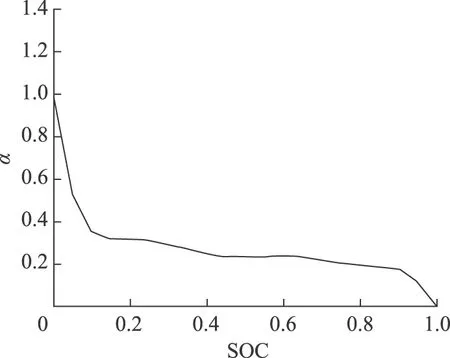
图6 权重变化曲线Fig.6 Weight change curve

由于采用多段恒流充电方法，整个充电过程共分为10段，需要将连续的权重变化曲线变换为各个恒流充电阶段内的定值。具体变换过程如下：在各个SOC(i) 阶段内(SOC<0.9)，取权重变化曲线在该阶段内的代数平均值作为此段内的权重值α(i)。

锂电池的整个充电过程中，变权重多段恒流充电方法是通过在各个恒流充电阶段内改变目标方程式(13) 中的权重值，从而可均衡考虑当前的充电速度和能量损耗。根据式(13)和各个恒流充电阶段内得到的权重值，可计算得到9个SOC段内的优化充电电流，计算结果见表5。

表5 各个SOC(i)段内对应的权重和优化充电电流

本文提出的变权重多段恒流充电方法主要指在整个充电过程中权重值是根据锂电池特性改变,以使当前充电电流与锂电池特性更加匹配，依据不同方法可设计出不同的权重变化曲线，而本文只是给出其中一条权重变化曲线实例。

4 实验与分析

根据本文提出的多段恒流充电方法和设计的权重变化曲线，对两种容量规格的磷酸铁锂电池(10 A·h和8.5 A·h)分别进行实验，并与恒流充电方式进行比较，结果见表6和表7。

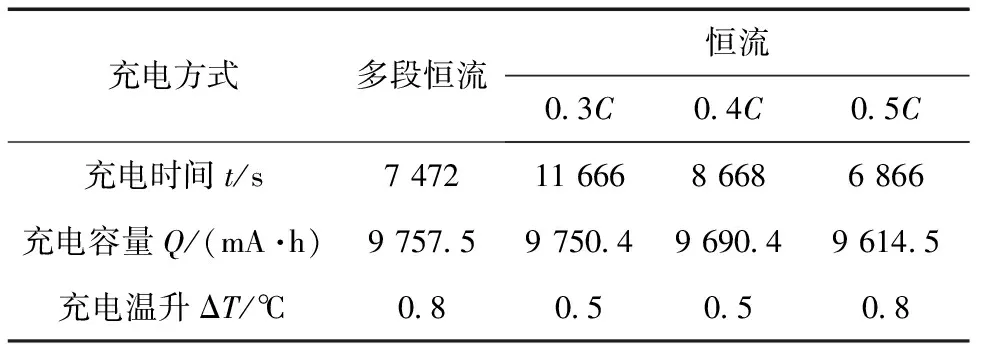
表6 10 A·h锂电池实验数据

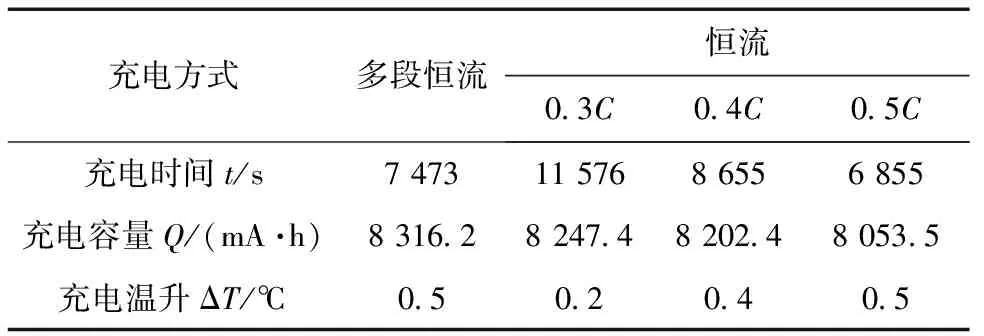
表7 8.5 A·h锂电池实验数据

由于本所提出的变权重多段恒流充电方法中的最后阶段采用0.2C电流充电直到锂电池端电压达到截止充电电压，这样能够使锂电池在较小充电电流条件下充入较多的电荷。当只采用单一电流恒流充电方法充电直到锂电池端电压达到截止充电电压时，若充电电流大于0.2C，则充入的电荷必然小于上述充电方法充入的电荷。由以上分析可知，无法准确确定上述变权重多段恒流充电方法所对应的单一电流恒流充电方法的等价倍率电流值(约0.47C)，若采用电流0.47C对锂电池进行单一电流恒流充电，所充入的电荷比本文方法充入的少，进而所需时间也必然短，然而这种对比实验没有实质性的对比效果。本文采用多组单一电流(0.3C、0.4C、0.5C和0.6C)恒流充电过程作为对比实验，以对比本文多段恒流充电方法与单一恒流充电方法的区别，从而能够更加全面地体现本文方法的特点。

由表6可知，本文提出的多段恒流充电方法与0.4C恒流充电方式相比，时间减少20 min，即充电时间缩短13.8%，充入的容量增加0.7%，温度升高0.3 ℃，但充电末期温度较低。与0.3C恒流充电方式相比，充入的容量近似相等，时间减少了70 min，即充电时间缩短36%，温度升高0.3 ℃，但充电末期温度较低。

充电过程中，10 A·h容量的锂电池电流、电压和温度变化曲线如图7所示。由图7可知，本文提出的充电方法具有如下特点：在充电初期，温升较快，随着充电电流逐渐减小，锂电池温度降低，这与本文假设锂电池温度特性的先验知识相符；在充电末期，锂电池端电压较低。因此，根据权重变化曲线，本文提出的充电方法能够达到预期目的。

图7 电流、电压和温度变化曲线Fig.7 Curves of current, voltage and temperature

随着充电的进行，本文方法中的充电电流逐渐减小，故可以减小电池内部的极化现象，即减小直流内阻两端的超电势，增加锂电池寿命。在充电末期，锂电池端电压降低，如将此方法应用到电池组可减小电池组端电压的不一致性，增加电池组充入的总电量，减弱电池组内个别单体电池的超电势，从而可增加电池组的整体寿命[8,21]。由于锂电池性能相对其他种类的蓄电池而言较好，且充放电过程持续的时间较长(本文均采用小倍率电流进行放电，一次放电过程需持续5 h)，若采用此充电方法对锂电池寿命进行实验分析，将会花费数年时间，故本文仅采用该充电方法开展了对锂电池寿命的定性分析，而没有作定量分析。

容量为8.5 A·h的磷酸铁锂电池的充电过程与10 A·h锂电池类似，在此不作赘述，只给出实验结果，见表7。以上实验结果说明，本文设计的多段变权重恒流充电方法适合不同容量的磷酸铁锂电池，根据锂电池特性所设计的权重变化曲线，能够满足预期充电要求，减小了充电时间，增加了充入电荷量。

5 结论

在均衡考虑锂电池内部能量损耗和充电速度的前提下，本文提出一种多段恒流充电方法。其要点是：①直流内阻测试方法可得到以SOC和充电电流为变量的直流内阻函数，从而为考虑锂电池损耗的快充方法提供了基础；②建立用于均衡能量损耗和充电速度的充电目标方程；③该方法基于极限电流设计变化的权重曲线，得到了多段恒流充电指令的工程方法。

实验结果表明上述方法具有如下优点：增加锂电池充入电荷量，降低电池端电压，降低锂电池温度，计算过程简单，便于实际应用。基于该方法和所用锂电池的具体特性，用户可进一步设计合适的权重变化曲线，以得到合适的充电电流指令。

[1] Takami N, Inagaki H, Tatebayashi Y, et al. High-power and long-life lithium-ion batteries using lithium titanium oxide anode for automotive and stationary power applications[J]. Journal of Power Sources, 2013, 244(15): 469-475.

[2] 陈息坤, 孙冬, 陈小虎. 锂离子电池建模及其荷电状态鲁棒估计[J]. 电工技术学报，2015, 30(15): 141-147. Chen Xikun, Sun Dong, Chen Xiaohu. Modeling and state of charge robust estimation for lithium-ion batteries[J]. Transactions of China Electrotechnical Society, 2015, 30(15):141-147.

[3] Chiu K C, Lin C H, Yeh S F, et al. Cycle life analysis of series connected lithium-ion batteries with temperature difference[J]. Journal of Power Sources, 2014, 263(1): 75-84.

[4] Waldmann T, Wilka M, Kasper M, et al. Temperature dependent ageing mechanisms in lithium-ion batteries —a post-mortem study[J]. Journal of Power Sources, 2014, 262(15): 129-135.

[5] 刘新天, 何耀, 曾国建, 等.考虑温度影响的锂电池功率状态估计[J].电工技术学报,2016, 31(13): 155-163. Liu Xintian, He Yao, Zeng Guojian, et al. State-of-power estimation for Li-ion battery considering the effect of temperature[J]. Transactions of China Electrotech-nical Society, 2016, 31(13): 155-163.

[6] Krishnan S, Hariharan. A coupled nonlinear equivalent circuit—thermal model for lithium ion cells[J]. Journal of Power Sources, 2013, 227(1): 171-176.

[7] Hussein A A, Batarseh I. A review of charging algorithms for nickel and lithium battery chargers[J]. IEEE Transactions on Vehicular Technology, 2011, 60(3): 830-838.

[8] 吴赟, 蒋新华, 解晶莹. 锂离子电池循环寿命快速衰减的原因[J]. 电池, 2009, 39(4): 206-207. Wu Yun, Jiang Xinhua, Xie Jingying. The reasons of rapid decline in cycle life of Li-ion battery[J]. Battery Bimonthly, 2009, 39(4): 206-207.

[9] Vo T T, Chen Xiaopeng, Shen Weixiang. New charging strategy for lithium-ion batteries based on the integration of Taguchi method and state of charge estimation[J]. Journal of Power Sources, 2015, 273(1): 413-422.

[10]Ikeya T, Sawada N, Murakami J. Multi-step constant-current charging method for an electric vehicle nickelmetal hydride battery with high-energy efficiency and long cycle life[J]. Journal of Power Sources, 2002, 105(1): 6-12.

[11]Liu Chuang, Han Min, Wang Xinzhe. A novel evolutionary membrane algorithm for global numerical optimization[J]. Information Sciences, 2012, 276: 727-732.

[12]Liu C L, Wang S C, Chiang S S. PSO-based fuzzy logic optimization of dual performance characteristic indices for fast charging of lithium-ion batteries[C]//IEEE 10th International Conference on Power Electronics and Drive Systems (PEDS), 2013: 474-479.

[13]Liu Y H, Teng J H, Lin Y C. Search for an optimal rapid charging pattern for Li-ion batteries using the ant colony system algorithm[J]. IEEE Transactions on Industrial Electronics, 2005, 57(5): 1328-1336.

[14]Liu Y H, Luo Y F. Search for an optimal rapid-charging pattern for Li-ion batteries using the taguchi approach[J]. IEEE Transactions on Industrial Electronics, 2010, 57(12): 3963-3971.

[15]Liu Y H, Hsieh C H, Luo Y F. Search for an optimal five-step charging pattern for Li-ion batteries using consecutive orthogonal arrays[J]. IEEE Transactions on Energy Conversion, 2011, 26(2): 654-661.

[16]Johnson V H. Battery performance models in ADVISOR[J]. Journal of Power Sources, 2002, 110(2): 321-329.

[17]何志超, 杨耕, 卢兰光, 等. 基于恒流外特性和的电池直流内阻测试方法[J]. 清华大学学报(自然科学版), 2015, 55(5): 532-537. He Zhichao, Yang Geng, Lu Languang, et al. Battery DC internal resistance test method based on the constant current external characteristics and SOC[J]. Journal of Tsinghua University (Science & Technology), 2015, 55(5): 532-537.

[18]冯飞, 宋凯, 逯仁贵, 等.磷酸铁锂电池组均衡控制策略及荷电状态估计算法[J]. 电工技术学报, 2015, 30(1): 22-29. Feng Fei, Song Kai, Lu Rengui, et al. Equalization control strategy and SOC estimation for LiFePO4battery pack[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 22-29.

[19]Notten P H L, Veld J H G O H, Beek J P G V. Boost charging Li-ion batteries: a challenging new charging concept[J]. Journal of Power Sources, 2005, 145(1): 89-94.

[20]Jiang Jiuchun, Liu Qiujiang, Zhang Caiping, et al. Evaluation of capable charging current of power Li-ion batteries based on polarization characteristics[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6844-6851.

[21]刘红锐, 张昭怀. 锂离子电池组充放电均衡器及均衡策略[J].电工技术学报, 2015, 30(8): 186-192. Liu Hongrui, Zhang Zhaohuai. The equalizer of charging and discharging and the balancing strategies for lithiumion battery pack[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 186-192.

(编辑 张洪霞)

A Multistage Current Charging Method for Li-Ion Battery ConsideringBalance of Internal Consumption and Charging Speed

LiuWei1WuHaisang2HeZhichao2SunXiaofeng3YangGeng2

(1.College of Mechanical and Electrical Engineering Cangzhou Normal University Cangzhou 061001 China 2.Department of Automation Tsinghua University Beijing 100084 China 3.Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province Yanshan University Qinhuangdao 066004 China)

A fast charging method should make a balance between battery′s safety/cycle life and charging time. For that the battery's temperature or energy loss should be controlled in the method. This paper proposed a charging method of Li-ion battery to balancing internal consumption and charging speed. Firstly, based on the constant current charging voltage curves of the Li-ion battery, the method gave a procedure to get the relationship of the internal resistances with stage of charge (SOC) and charge currents. Then the energy loss function was simplified and an objective function was designed for balancing charging time and the loss. Finally, for real time implementation, a multistage current charging curve is designed with different balance weight factors in each stage. Experiment shows the advantages.

Li-ion battery internal direct current resistance, charging time, energy loss, constant current charging, weight factor

国家自然科学基金项目资助(U1510208,61273045和51361135705)。

2016-01-11 改稿日期2016-04-25

TQ152

刘 伟 男，1990年生，硕士研究生，研究方向为动力锂电池的应用。

E-mail：liuw0214@sina.com(通信作者)

吴海桑 男，1990年生，硕士研究生，研究方向为动力锂电池管理系统。

E-mail：whs19900810@sina.com