基于组合继电反馈的永磁同步直线电机推力波动辨识方法

张 翔 叶佩青，2 张 辉，2

(1.清华大学机械工程系 北京 100084 2.摩擦学国家重点实验室(清华大学) 北京 100084)



基于组合继电反馈的永磁同步直线电机推力波动辨识方法

张 翔1叶佩青1，2张 辉1，2

(1.清华大学机械工程系 北京 100084 2.摩擦学国家重点实验室(清华大学) 北京 100084)

在永磁同步直线电机中，由齿槽效应和端部效应引起的推力波动是制约其动态性能的重要因素。提出一种基于组合继电反馈的推力波动辨识方法，且利用辨识结果实现推力波动的补偿。针对某直驱进给实验平台，首先建立其动力学模型，设计基于理想继电环节和含有死区的迟滞继电环节相结合的信号激励源;其次利用描述函数对各非线性环节进行谐波线性化进而获取各环节的双输入描述函数，再根据非线性系统极限环存在条件确定系统待辨识参数的解析表达式;最后，通过仿真和实验验证了该方法的可行性和准确性。实验表明当直驱进给系统匀速运动时，含有推力波动补偿时伺服系统的推力电流波动比补偿前降低了46.3%，其跟踪误差的方均根由34.1 μm降至19.3 μm。

直线电机 极限环 参数辨识 继电反馈 推力波动

0 引言

目前永磁同步直线电机已广泛应用于数控机床、医疗设备、半导体制造及精密仪器设备中，并起到重要作用。由于直线电机直接与执行机构连接，在提高进给系统传动刚度的同时，其传动精度和可靠性也得以明显改善。此外，直线电机简化中间传动机构，在提高空间利用率的同时消除了由传动机构带来的摩擦或间隙等非线性因素，为提高直线伺服系统动态性能提供可能[1]。但任何作用在执行机构输出端的负载或扰动也将无缓冲地作用在电机输出端，如直线电机的推力波动、执行机构摩擦力以及负载突变等[2]。上述干扰因素中，推力波动主要由直线电机结构所致，主要包括端部磁场开断产生的端部定位力和内部齿槽结构引起的齿槽定位力，二者均与电机初级和次级的相对位置存在周期性关系，是电机自身的重要属性[3]。推力波动的存在对直驱系统的动态性能具有重要影响，因此准确高效地检测直线电机的推力波动对于提高直线电机动态性能具有重要意义。

为抑制或降低直线电机推力波动对伺服系统的影响，国内外学者进行了大量研究，现将解决方案分为优化或改进直线电机设计结构[4-6]和在控制过程中对推力波动进行观测或补偿[7-9]两类。文献[10]针对圆筒型直线电机的永磁体形状、充磁方向等进行优化设计，使推力波动得到改善，但通过结构优化的方法抑制推力波动会增加生产成本且易引起其他指标的退化。因此在控制器中通过辨识、补偿推力波动是抑制其影响的另一重要途径。在直线电机推力波动的辨识中按照其模型是否已知将其分为基于模型和无模型辨识。文献[11]根据已知形式的推力波动，提出一种基于神经网络的辨识方法，通过系统输入输出对推力波动的未知参数进行辨识和补偿，由于此方法的辨识精度对样本数据库的敏感性强，因此为保证辨识精度，需要进行大量实验获取样本数据。文献[12]提出一种基于扰动观测器的方法，将直线电机推力波动作为系统扰动，通过提取控制器输入和位置输出进行实时观测并补偿，但其观测与补偿效果受到被测信号所含高频噪声的影响。文献[13]利用一种特殊机构测试推力波动，根据相同测试条件不同运行方向将摩擦力抵消进而获取推力波动，但该方法对电机尺寸有所限制，难以得到普遍应用。

继电反馈辨识方法是一种基于非线性系统稳定极限环的幅值和频率等信息而获取系统模型参数的方法，且在辨识过程中无需额外执行机构或信号激励装置。由于此方法简单易行，已广泛应用于过程控制领域的参数辨识中。此外已有相关学者研究利用继电反馈方法辨识伺服系统的静摩擦力、库伦摩擦力和黏滞摩擦力，并通过仿真和实验验证了方法的正确性[14，15]。新加坡学者S.L.Chen首次提出应用继电反馈方法对直驱进给伺服系统的推力波动进行辨识，通过迟滞继电环节产生的方波作为激励信号实现辨识[16]。由于继电反馈辨识本质上是利用描述函数将非线性系统线性化来求解待辨识参数解析表达式，而方波激励信号中谐波含量较高，使参数辨识的精度受限。

综上所述，为降低激励信号中的谐波含量以提高参数辨识精度，本文提出一种基于组合继电反馈的直线电机推力波动辨识方法。针对直驱进给系统，首先建立其动力学模型，其次设计了基于理想继电环节和含死区的迟滞继电环节的组合继电激励，并根据极限环存在条件及谐波线性化理论求解待辨识参数的解析表达式，最后通过仿真计算和实验验证该辨识方法的可行性和准确性。

1 直驱进给系统动力学建模

本文以直驱进给实验平台为研究对象，平台以圆筒型直线电机为驱动元件,以滑动导轨为传动元件，建立其动力学模型为

f(t)=Kfi(t)

(1)

(2)

式中，f(t)、fr(x)、ff和fΔ分别为直线电机驱动力、推力波动、摩擦力和其他干扰；Kf为推力系数；i(t)为加载至线圈的电流值；m为负载质量；x(t)为执行机构的实时位置。由于直驱平台采用滑动导轨作为传动方式，因此主要考虑由黏性摩擦fv和库伦摩擦fc组成的摩擦力

(3)

另外根据文献[16]可知，在忽略推力波动高次谐波的情况下，可将fr(x)简化为

fr(x)=Csin(Ωx+θ)=C1cos(Ωx)+C2sin(Ωx)

(4)

由式(1)～式(4)可得

(5)

其中

(6)

根据式(5)直驱进给系统线性部分可表示为

(7)

式中，a=fv/m；b=1/m。

2 非线性系统参数辨识

2.1 组合继电环节的设计

为使上述非线性系统能够产生稳定的极限环，即在某种激励信号作用下，系统具有频率和幅值稳定的位置输出。因此设计基于理想继电环节和含有死区的迟滞继电环节相结合的信号激励源，其中理想继电环节表达式为

(8)

式中，e为跟踪误差即指令输入和反馈输出的差值。如图1所示含有死区的迟滞继电环节定义为

(9)

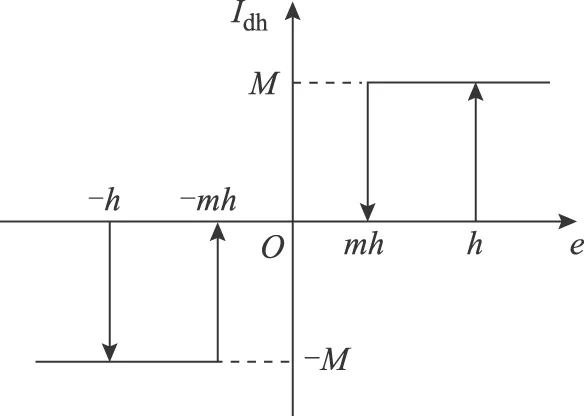
图1 含有死区的迟滞继电环节Fig.1 A hysteretic relay with dead zone

根据组合继电环节可得待辨识系统如图2所示。当非线性系统出现稳定极限环时，由非线性系统谐波线性化理论可假设其误差形式为e(t)=Asin(ωt)+B，进而利用描述函数可建立待辨识参数与组合继电增益、系统稳定输出的幅值及频率的解析关系。

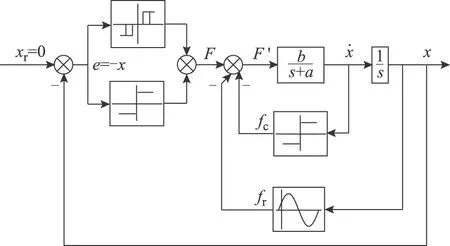
图2 继电反馈辨识系统Fig.2 Identification system based on relay feedback

2.2 非线性环节的描述函数

为便于分析图2所示继电反馈辨识系统，将其转换为含有线性部分和非线性部分的等效框图如图3所示，其中非线性部分包括理想环节、含有死区的迟滞环节、推力波动及库仑摩擦力，线性部分包括负载和黏性摩擦力。

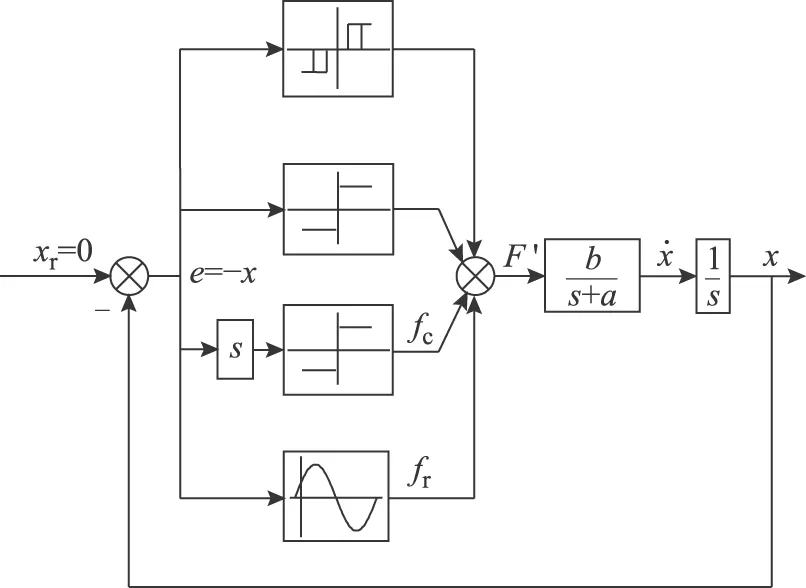
图3 辨识系统等效框图Fig.3 Equivalent block of identification system

将跟踪误差e=-x带入式(6)可得

F′=Kfi(t)+fsgn(e)-C1cos(Ωe)+C2sin(Ωe)

(10)

针对图3中各非线性环节，利用描述函数对其进行谐波线性化，求解各环节对应的描述函数。由假设的跟踪误差形式可知，误差包括交流分量和直流分量，因此下面将利用描述函数法求解各环节对应的双输入描述函数(DualInputDualFunctions，DIDF)。首先考虑含有死区的迟滞环节

(11)

(12)

式中，Nah为交流分量对应的描述函数；Nbh为直流分量对应的描述函数。其中

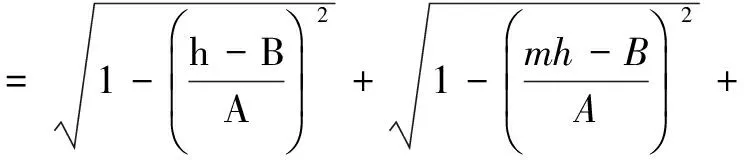
其次，求解库伦摩擦力的DIDF，由于库伦摩擦前含有积分环节，其直流分量对应的描述函数为零。

(13)

Nbf=0

(14)

式中，Naf为交流分量对应的描述函数；Nbf为直流分量对应的描述函数。

再次，推力波动的DIDF如式(15)、式(16)所示。

(15)

(16)

式中，Ji(ΩA)为ΩA所对应的i阶贝塞尔函数值。

利用谐波线性化方法只考虑各非线性环节的基波分量而忽略其他高次谐波。因此，根据叠加原理可得在交流分量和直流分量输入下待辨识系统非线性部分的描述函数为

Na=Nah+Nar+Naf+NaI

(17)

Nb=Nbh+Nbr+NbI

(18)

2.3 非线性系统产生极限环的条件

根据非线性系统产生稳定极限环的条件，其非线性部分和线性部分的描述函数需满足

Na(A,B,ω)G(jω)=-1

(19)

Nb(A,B,ω)=0

(20)

式(19)成立需要其实部和虚部分别满足条件，由此可得

(21)

2sin(ΩB)J1(ΩA)C1+2cos(ΩB)J1(ΩA)C2

(22)

由式(20)成立可知

2C2sin(ΩB)-2C1cos(ΩB)

令

定义α=a/b，β=1/b。

由此可知系统待辨识参数为α，β，C1，C2和f。

2.4 待辨识参数的求解

根据2.3节中非线性系统极限环产生条件可得三个方程，而系统中含有5个待辨识参数，因此至少需要在两组不同继电增益条件下进行实验，才能实现对全部待辨识参数的求解。假设两组继电反馈实验中继电增益分别为m1、m2、M1、M2、h1、h2、D1、D2，位置输出的幅值、频率和偏置分别为A1、A2、B1、B2、f1、f2，根据以上信息可求解待辨识参数的解析表达式为

(23)

(24)

(25)

(26)

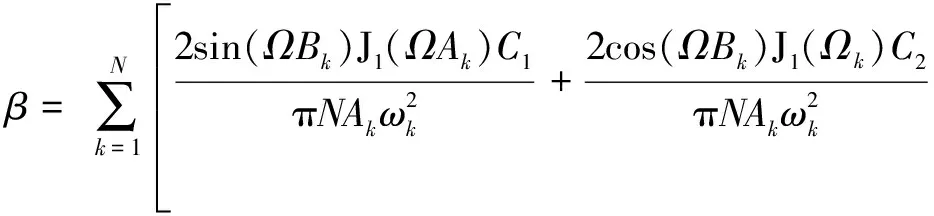
(27)

在式(23)～式(27)中，继电反馈的增益可以根据控制器中的设计值确定，而位置输出的幅值、频率和偏置则需要分析确定。由于在2.1节的分析中已知输出信号的形式，因此在稳定输出中提取有限周期稳定的位置输出，利用最小二乘法对已知形式的信号和实际位置输出进行拟合求解输出信号的幅值、频率和偏置。

3 仿真验证

为确定所提辨识方法的有效性和准确性，通过仿真计算进行验证。假定上述直线伺服进给系统的动力学模型中的待辨识参数为:a=4,b=40,f=0.4,C1=0.5,C2=0.866。

仿真过程中采样时间为0.1ms，参数Ω为0.2π。利用组合继电环节产生的信号激励此非线性系统的极限环。

3.1 非线性系统极限环产生条件

图4为在一定继电增益条件下的位置输出。根据式(21)可知，在m为1时要求极限环振荡频率或幅值为负值，这在实际系统中是不可能的。因此在图4所示的继电增益条件下系统不能产生稳定极限环，仿真实验结果与理论推导结论一致。

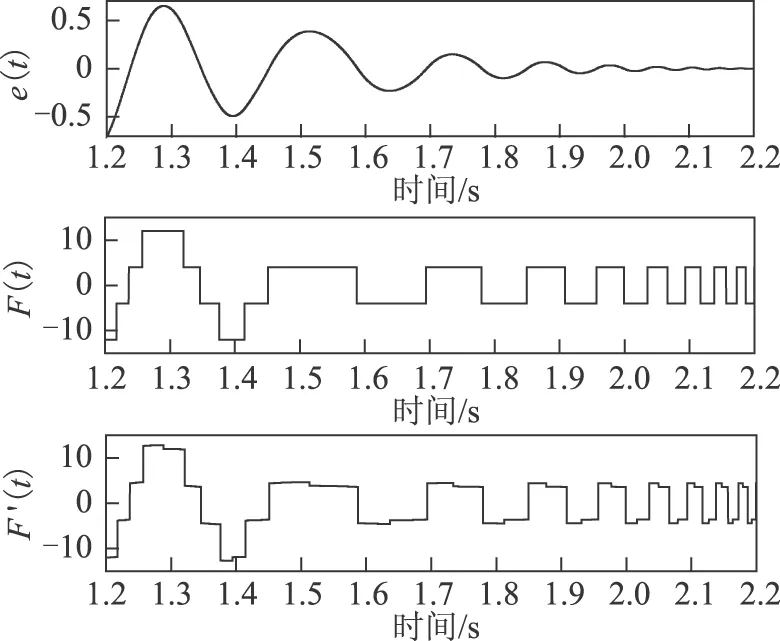
图4 M=8，D=4，h=0.4，m=1，θ=0位置输出Fig.4 M=8，D=4，h=0.4，m=1，θ=0 position output

根据图4仿真结果，调整非线性环节的继电增益如图5所示，系统可以产生稳定输出，且由于系统中θ=0，因此系统位置输出关于e(t)=0对称。

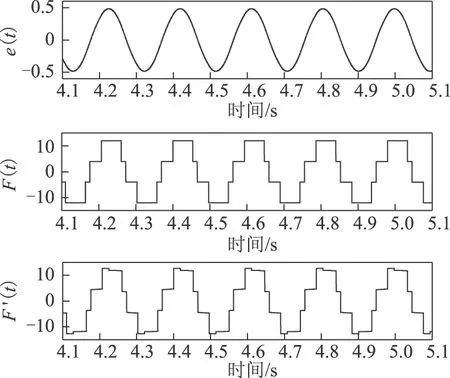
图5 M=8，D=4，h=0.4，m=0.5，θ=0位置输出Fig.5 M=8，D=4，h=0.4，m=0.5，θ=0 position output

在仿真中设置推力波动相位项θ=π/4，通过图6仿真结果可见推力波动中存在偶函数项，导致系统输出的极限环含有偏置。本文所提辨识方法即根据系统输出的偏置项求解推力波动的幅值和相位。

3.2 参数辨识

在仿真实验中，假设推力波动相位θ=π/6，其余参数不变。由2.4节的分析可知，为求解系统全部待辨识参数，需按图7、图8中的继电增益参数设置进行两组辨识实验。

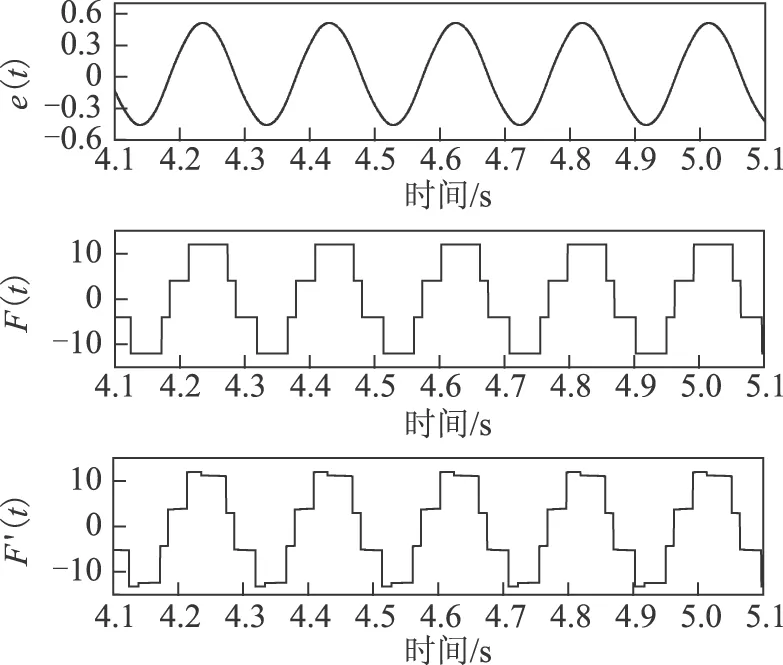
图6 M=8，D=4，h=0.4，m=0.5，θ=π/4位置输出Fig.6 M=8，D=4，h=0.4，m=0.5，θ=π/4 position output

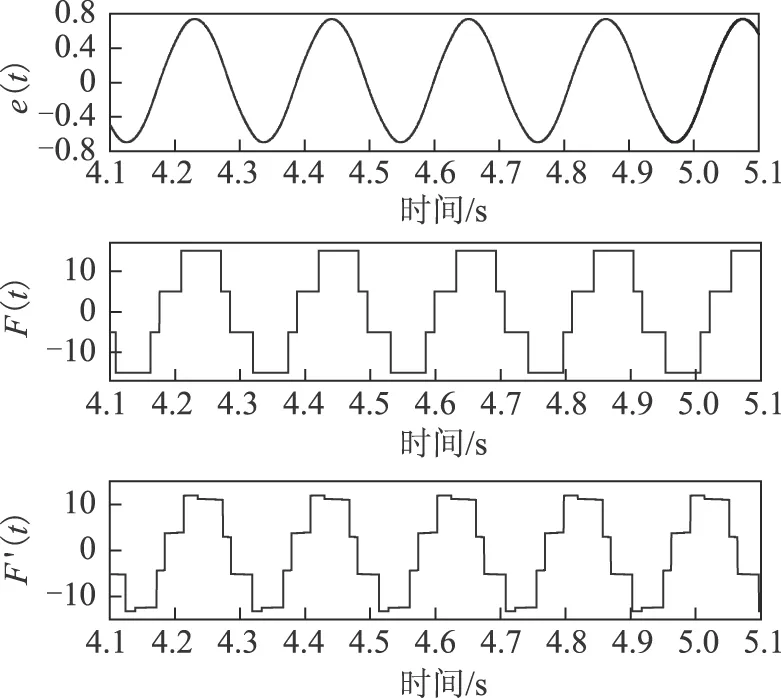
图7 M=10，D=5，h=0.6，m=0.5，θ=π/6位置输出Fig.7 M=10，D=5，h=0.6，m=0.5，θ=π/6 position output

图8 M=8，D=4，h=0.4，m=0.3，θ=π/6位置输出Fig.8 M=8，D=4，h=0.4，m=0.3，θ=π/6 position output

利用2.4节中所述对输出信号的提取方法可得ω1=29.740 5，A1=0.717 5，B1=0.023 9，ω2=30.728 6，A2=0.601 2，B2=0.029 5，再通过待辨识参数的解析表达式可求解得到a=4.081，b=40.322 6，C1=0.450 7，C2=0.862 0，f=0.394 9。

3.3 与迟滞继电反馈辨识的对比

由于继电反馈辨识本质上是利用描述函数将非线性系统线性化来求解待辨识参数解析表达式，因此在保证非线性系统极限环存在的基础上，辨识过程中理想激励信号为固定频率的正弦输出。为此将图7仿真实验中的激励信号、采用迟滞继电环节辨识的激励信号[15]与理想激励信号进行对比，如图9所示。在对上述激励信号进行快速傅里叶变换后可得其谐波误差分量如图10所示，由此可见组合继电反馈的谐波含量明显优于迟滞继电反馈的谐波含量，可以有效减小激励信号的谐波误差。

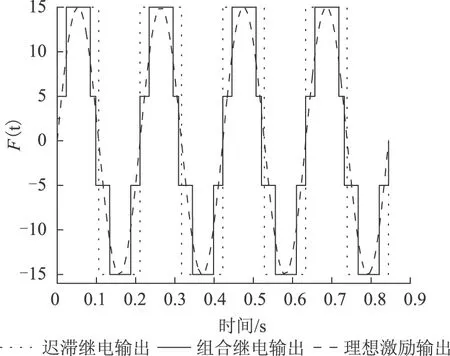
图9 继电激励信号与理想激励信号对比Fig.9 Comparison between relay excitation signal and ideal excitation signal

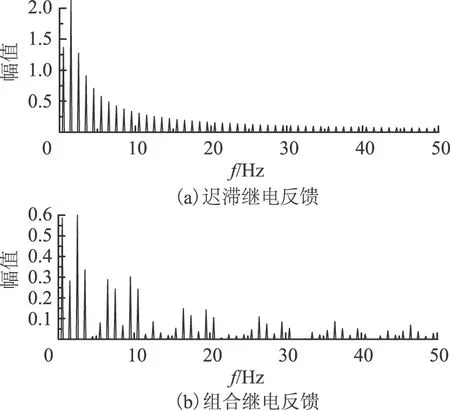
图10 继电激励信号的谐波误差分量Fig.10 Harmonic error component of relay excitation signal

表1为采用组合继电环节和迟滞继电环节的仿真辨识结果对比，通过对具有相同模型参数的伺服系统的仿真辨识可见，组合继电反馈的最大参数辨识误差可以减小至9.86%，比迟滞继电反馈辨识方法有所提高。

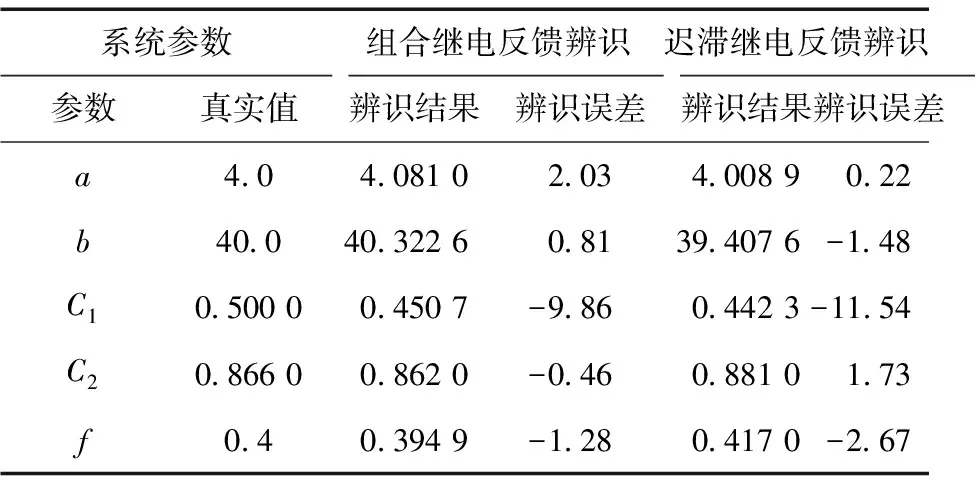
表1 仿真辨识结果

4 实验验证

4.1 基于继电反馈的系统参数辨识

图11为利用圆筒型直线电机作为驱动元件的直驱进给实验平台，主要包括：①BeckHoff公司的PLC控制器，控制器采样时间可调，最小控制周期为50 μs；②利用TOSHIBA公司生产的THS119霍尔传感器进行位置检测，传感器检测分辨率为2.5 μm；③课题组研发的圆筒型直线电机和伺服驱动器，相关参数见表2，负载的传动方式为滑动导轨。

图11 直驱进给平台实物图Fig.11 Direct-drive feed platform in lab environment

表2 电机及驱动参数说明

在进行系统参数辨识前，首先需要确定推力波动的特征频率。利用实验方法[17]确定的圆筒型直线电机推力波动特征频率Ω为0.603 2 rad/mm。然后在图11所示平台按照相应继电增益系数进行辨识实验，实验结果如图12、图13所示。

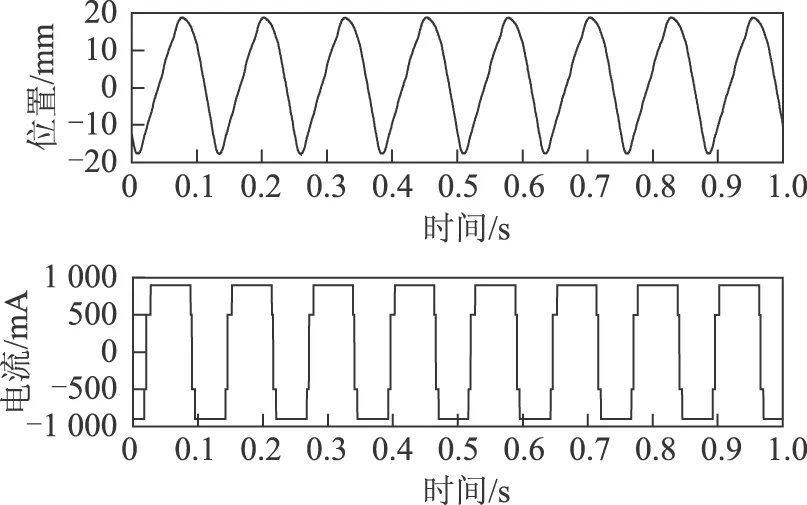
图12 M1=40，D1=50，h1=2 000，m1=0.5位置输出Fig.12 M1=40，D1=50，h1=2 000，m1=0.5 position outputs

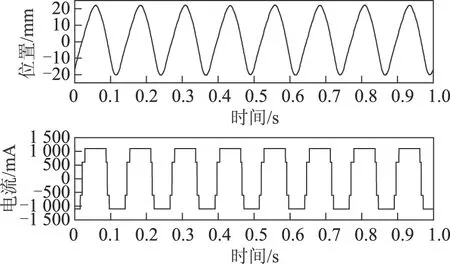
图13 M1=50，D1=60，h1=2 500，m1=0.6位置输出Fig.13 M1=50，D1=60，h1=2 500，m1=0.6 position outputs

由图12、图13的继电反馈辨识实验可以得到两组位置输出信号的频率、幅值和直流偏置分别为49.155 Hz、18.186 mm、0.522 5 mm及49.247 Hz、21.106 mm和0.991 mm，再利用式(23)～式(27)中的解析表达式可以确定系统待辨识参数为a=0.219 9，b=8.096 3，C1=-0.882 0，C2=-3.092 0，f=0.021 2。

4.2 推力波动补偿对控制性能的影响

为便于验证辨识结果的正确性，针对图11直线进给平台使其处于往复运动状态，并设定其往复运动行程及速度分别为40 mm和5 mm/s，运动过程中控制器参数见表2。通过对比直线电机匀速运动状态下推力电流和位置跟踪误差进而分析推力波动前馈补偿对直驱伺服控制性能的影响(该方法也适用于非匀速运动状态)。由图14可见，基于组合继电反馈推力波动前馈补偿的推力电流波动显著减小，其波动量较无补偿和基于迟滞辨识的前馈补偿分别降低了46.3%和30.9%。图15为不同补偿状态下伺服系统的跟踪误差，其跟踪误差的方均根由无补偿时的34.1 μm分别降至21.7 μm(迟滞辨识补偿)和19.3 μm(组合继电辨识补偿)。

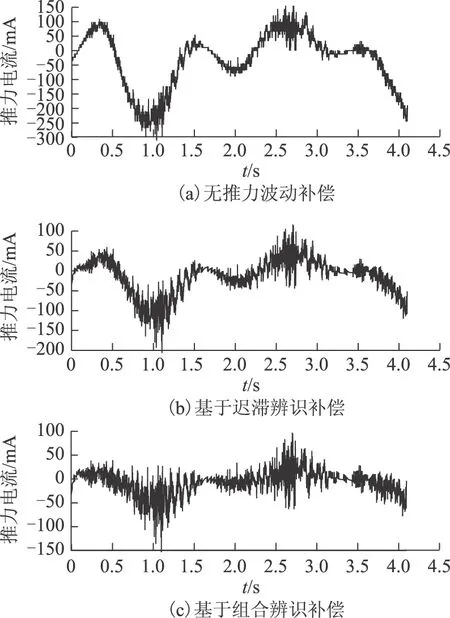
图14 匀速运动状态不同补偿的推力电流Fig.14 Thrust current with different compensation methods under uniform motion

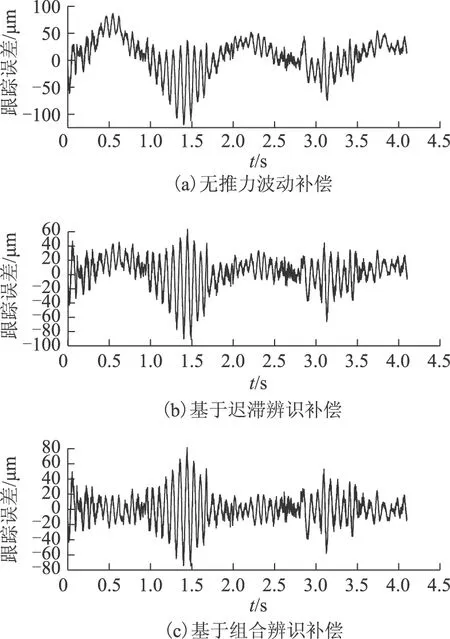
图15 匀速运动状态不同补偿的跟踪误差Fig.15 Tacking error with different compensation methods under uniform motion

5 结论

1)针对直线进给平台,建立其传动系统动力学模型，为利用非线性系统极限环进行系统参数辨识，所设计的继电环节由理想和含有死区的迟滞环节组成，用于提供激励信号。

2)利用描述函数法对系统中各非线性环节进行谐波线性化，得到各环节的DIDF，并根据非线性系统极限环产生条件求解得到系统待辨识参数的解析表达式。

3)本文通过仿真验证了辨识方法的有效性和准确性，且通过实验测试表明，在直线进给机构处于低速且匀速运动的状态下，含有直线电机推力波动补偿下推力电流波动降低了46.3%，直驱伺服跟踪误差方均根由34.1 μm降至19.3 μm。综上所述，利用本文辨识方法获取的推力波动模型有效，可以用于改善伺服系统的控制性能。

[1] 陆华才，江明，郭兴众，等.永磁直线同步电机推力波动约束[J].电工技术学报，2012，127(3)：128-132. Lu Huacai，Jiang Ming，Guo Xingzhong，et al. Thrust ripple suppression for permanent magnet linear synchronous motor[J].Transactions of China Electrotechnical Society，2012，127(3)：128-132.

[2] Lu S W，Tang X Q，Song B，et al.Identification and compensation of force ripple in PMSLM using a JITL technique[J]. Asian Journal of Control，2015，17(3)：1-10.

[3] Ahn H S，Chen Y Q，Dou Huifang.Static-periodic adaptive compensation of cogging and coulomb friction in permanent magnet linear motor[C]//IEEE Transactions on Magnetics，2005，41(1)：90-98.

[4] 赵玫，邹继斌，王骞，等.圆筒型横向磁通用此直线电机的基础研究[J].电工技术学报，2014，29(1)：80-89. Zhao Mei，Zou Jibin，Wang Qian，et al.Fundamental research of tubular transverse flux permanent magnet linear machine[J].Transactions of China Electrotechnical Society，2014，29(1)：80-89.

[5] 黄磊，胡敏强，刘静，等.双边长初级磁通切换永磁直线电机推力波动分析及抑制[J].电工技术学报，2014，29(11)：10-19. Huang Lei，Hu Minqiang，Liu Jing，et al.Analysis and suppression of the thrust ripple in a double-sided long primary flux-switching permanent magnet linear motor[J].Transactions of China Electrotechnical Society，2014，29(11)：10-19.

[6] 寇宝泉，张赫，郭守仑，等.辅助极一体式永磁同步直线电机端部定位力抑制技术[J].电工技术学报，2015，30(6)：106-113. Kou Baoquan，Zhang He，Guo Shoulun，et al.End effect detent force reduction for permanent magnet linear synchronous motors with auxiliary poles one-piece structure[J].Transactions of China Electrotechnical Society，2015，30(6)：106-113.

[7] Naso D，Cupertino F，Turchiano B.Precise position control of tubular linear motors with neural networks and composite learning[J].Control Engineering Practice，2010，18(5)：515-522.

[8] Lu Lu，Yao Bin，Chen Zheng，et al.Adaptive robust control of a linear motor driven precision industrial gantry with improved cogging force compensation[C]//2008 ASME Dynamic Systems and Control Conference，2008.

[9] 张代林，陈幼平，艾武，等.基于观测器模型的直线电机干扰抑制技术的研究[J].中国电机工程学报，2007，27(12)：14-18. Zhang Dailin，Chen Youping，Ai Wu，et al.Research on disturbance suppression technology for linear motors based on a disturbance observer model[J].Proceedings of the CSEE，2007，27(12)：14-18.

[10]崔连峰, 郝玉丽. 机床用永磁直线同步电机推力波动的优化设计[J]. 微电机, 2012, 45(10): 29-33. Cui Lianfeng, Hao Yuli. Thrust fluctuations optimal design of PMLSM for machine tool[J]. Micromotors, 2012, 45(10): 29-33.

[11]Zhang Dailin，Chen Youping，Ai Wu，et al.Force ripple suppression technology for linear motors based on propagation neural network[J].Chinese Journal of Mechanical Engineering，2008，21(2)：13-16.

[12]Sung H C，Park J B，Joo Y H.Observer-based sampled-data control for nonlinear systems：Robust intelligent digital redesign approach[J].International Journal of Control，Automation，and System，2014，12(3)：486-496.

[13]Villegas F J, Hecker R L, Pena M E, et al. Modeling of a linear motor feed drive including pre-rolling friction and aperiodic cogging and ripple[J]. International Journal of Advanced Manufacturing Technology, 2014, 73(1): 267-277.

[14]Tan K K，Lee T H，Huang S N，et al.Friction modeling and adaptive compensation using a relay feedback approach[J].IEEE Transactions on Industrial Electronics，2001，48(1)：169-176.

[15]Chen S L, Tan K K, Huang S. Identification of coulomb friction-impeded systems with a triple-relay feedback apparatus[J]. IEEE Transactions on Control System Technology, 2012, 20(3): 726-737.

[16]Chen S L，Tan K K，Huang S N，et al.Modeling and compensation of ripples and friction in permanent-magnet linear motor using a hysteretic relay[J].IEEE/ASME Transactions on Mechatronics，2010，15(4)：586-594.

[17]卢少武，唐小琦，周凤星，等.永磁同步直线伺服系统的纹波推力补偿[J].西安交通大学学报，2014，48(2)：106-110. Lu Shaowu，Tang Xiaoqi，Zhou Fengxing，et al.Force ripple compensation for permanent magnet linear servo system[J].Journal of Xi′An Jiao Tong University，2014，48(2)：106-110.

(编辑 于玲玲)

An Identification Method of Force Ripple in Permanent Magnet Synchronous Linear Motors Based on the Combined Relay Apparatus

ZhangXiang1YePeiqing1，2ZhangHui1，2

(1.Department of Mechanical Engineering Tsinghua University Beijing 100084 China 2.The State Key Laboratory of Tribology Tsinghua University Beijing 100084 China)

Force ripples，caused by slot force and end force，are the significant factor which restricts the dynamic performance of linear motors.As a consequence，a new identification method based on the relay feedback was proposed to model and compensate for the force ripples in linear motors.Taking the direct feed platform as a researching object，the dynamic of the system was modeled and a signal source which included an ideal relay component and a hysteresis relay component along with dead zone was designed firstly.Hence，dual input description functions were obtained by implementing the method of describe function to linearize the designed relay components.Furthermore，the analytical expressions of the identified parameters in the nonlinear system were solved according to the requirement for oscillation.Finally，simulation study has been carried out for validating the feasibility and accuracy of the method while relevant experiments were conducted on the platform.Experiment results have shown that the thrust current fluctuation was reduced 46.3% while the RMSE of the tracking error can be reduced from 34.1 μm to 19.3 μm.

Linear motors，oscillation，parameter identification，relay feedback，force ripple

国家科技支撑计划项目(2015BAI03B00)、清华大学摩擦学国家重点实验室重点项目(SKLT12A03)及北京市科技计划项目(Z141100000514015)资助。

2016-03-30 改稿日期2016-09-26

TM351

张 翔 男，1989年生，博士研究生，研究方向为伺服控制技术。

E-mail：xiang-zhang12@mails.tsinghua.edu.cn

叶佩青 男，1963年生，研究员，博士生导师，研究方向为伺服驱动技术、数控技术与装备。

E-mail：yepq@tsinghua.edu.cn(通信作者)