自适应内联EESM无位置传感器控制

尚 敬 年晓红 刘 丽 南永辉

(1.中南大学信息科学与工程学院 长沙 410083 2.中车株洲电力机车研究所有限公司 株洲 412001)



自适应内联EESM无位置传感器控制

尚 敬1，2年晓红1刘 丽2南永辉2

(1.中南大学信息科学与工程学院 长沙 410083 2.中车株洲电力机车研究所有限公司 株洲 412001)

针对电励磁同步电机(EESM)的转子位置角辨识问题，提出了一种非线性的自适应内联观测器转子位置辨识方法。首先建立电励磁同步电机的扩展模型，然后对其进行分离设计，得到两个相互关联的子系统，并分别设计了两个子系统的反馈增益，构成自适应内联观测器，最后运用李雅普诺夫稳定性定理证明了所提方法的稳定性。该方法能够根据测量的电压和电流信号，辨识得到电机的速度、位置角以及q轴电感等信息；并将辨识信息反馈回控制回路以进一步优化电机的控制性能。仿真结果表明，该方法能够在电动和发电状态下实现宽转速范围内稳定运行，而且q轴电感的辨识值能够快速准确地跟随真实值，实验结果进一步验证了所提方法的有效性。

内联观测器 电励磁同步电机 无位置传感器 稳定性分析

0 引言

电励磁同步电机(Electrically Excited Synchronous Motor，EESM)具有功率因数高、转动惯量小、过载能力强等优点，被广泛应用于压缩机驱动、冶金轧机主传动、风力发电等大功率传动领域[1，2]。其控制的精确度依赖于传感器所获得的位置和速度信息，但传感器的引入存在增加系统成本、维护困难、影响系统的可靠性等缺点[3]，并且在直驱型风力发电系统等一些特殊场合很难安装位置传感器。因此，针对大功率电励磁同步电机的无位置传感器控制技术近年来已成为研究的热点。

目前，针对电机转速和位置辨识的方法主要分为两大类：一类是基于电机凸极效应的方法，这类方法主要有高频注入法[4，5]，该方法主要在中低速时起作用，高速下由于注入信号与基频信号的频率接近，使得滤波器的分辨率降低，辨识效果变差。另一类是基于电机模型的方法，这类方法主要有直接计算法[6]、反电动势估计算法[7]、模型参考自适应算法[8]、滑模观测器方法[9，10]以及卡尔曼滤波方法[11，12]，其中，直接计算法、反电动势估计算法和模型参考自适应算法的优点是实现简单，但都依赖于电机的参数，易受电机参数变化的影响。滑模观测器方法和卡尔曼滤波方法具有良好的鲁棒性，但滑模观测器本身存在抖动的特性，卡尔曼滤波方法则存在实时计算量大、动态响应不理想的问题。因此需寻求一种鲁棒性强，在宽速度范围内具有良好动、静态性能的无位置传感器控制方法。

内联的思想[13]是由G.Besancon等提出的一种针对非线性系统的处理方法，此后针对电机的无位置传感器控制涌现出大量的基于内联观测器方法[14-17]。该方法应用于电机系统的优点是能够辨识出电机的位置和速度信息，同时能够实现某些关键参数的在线辨识，并对电机参数的变化具有鲁棒性，但该方法目前都是应用于小功率的感应电机和永磁同步电机，并且辨识的电机参数大都是定子电阻，以提高系统在低速时的性能。电励磁同步电机作为一种具有强耦合性的非线性对象，其电感易受磁路饱和的影响而发生较大变化，极大地降低了控制系统的性能。但目前对电励磁同步电机电感辨识的文献较少，其电感辨识在国内外也是一个难点。文献[18]提出了一种用最小二乘法来近似电感的方法，但该方法较复杂且运算量较大，较难实现。

本文提出了一种自适应内联观测器的方法应用于电励磁同步电机，该方法能观测电机的转速、位置以及q轴电感，并利用观测的q轴电感修正控制模型，使得电机无论在电动状态下还是在发电状态下都能在宽速度范围内保持高功率因数运行。仿真和实验结果验证了所提方法的有效性。

1 数学模型

电励磁同步电机在dq旋转坐标系下的数学模型为常微分线性方程组，其电压、磁链方程分别为

(1)

(2)

式中，usd、usq分别为定子电压的d、q轴分量；isd、isq分别为定子电流的d、q轴分量；if为励磁绕组电流；Rs为定子电阻；Rf为励磁绕组电阻；Lad为d轴电枢反应电感；ω为电气角频率；ψsd、ψsq分别为定子磁链的d、q轴分量；uf为励磁绕组电压；ψf为励磁磁链；Lsd、Lsq、Lf分别为d、q轴总电感和励磁绕组总电感。

根据式(1)和式(2)以及电机的运动方程，推导得到电励磁同步电机的状态方程为

(3)

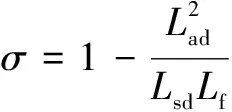
(4)

式中，f为粘滞摩擦系数；np为极对数；J为转动惯量。

考虑到定子电阻、负载转矩与q轴电感相对于转速的变化来说比较缓慢，因此可以得到

(5)

由此，式(3)～式(5)构成了电励磁同步电机的扩展数学模型。

2 内联观测器

2.1 内联观测器设计

若式(3)～式(5)满足如下两个条件[15]：①子系统的输入是持续的有界激励；②每个子系统都能用另外一个子系统的变量。那么，系统可以写成如下子系统的形式，其中Ω1表示第一个子系统，Ω2表示第二个子系统。

(6)

(7)

其中

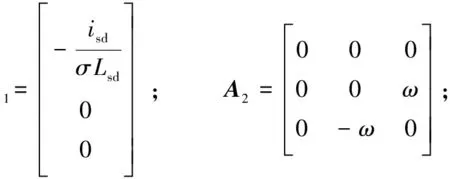
在实际的控制系统中，电机变量都是有界的。它们的实际范围定义为集合 I，其中R7代表具有7个变量的实数集。

(8)

电机其他参数的变化也都是有界的，而且变化量较小，这里省略其范围定义。

由式(8)知，前面所述假设①、②两个条件是成立的，而且子系统式(6)和式(7)能满足如下条件：

1)A1(x2)相对于x2满足全局Lipschitz条件。

2)g1(u,y,x1,x2)相对于x1和x2满足全局Lipschitz条件。

3)A2(x1)相对于x1满足全局Lipschitz条件。

4)g2(u,y,Rs,x1,x2)相对于x1和x2满足全局Lipschitz条件。

5)g1(u,y,x1,x2)和g2(u,y,Rs,x1,x2)相对于(u,y)满足一致有界。

那么，可对子系统Ω1和Ω2设计如下自适应内联观测器。

(9)

(10)

式中，λ1和λ2为正常数。

因此，得到自适应内联观测器的结构框图如图1所示，整个系统的输入量为：αβ相定子电压和三相定子电流、励磁电压和励磁电流。其中，自适应内联观测器主要由Ω1和Ω2两个子系统(即式(9)和式(10)所代表的子系统)的观测器组成，Ω1观测器的输出为d轴电流、转速、位置角、定子电阻和负载转矩，Ω2观测器的输出为q轴电流和电感以及d、q轴上的磁链。一个子系统的输出能作为另外一个子系统的输入，两个子系统相互关联，共同构成自适应内联观测器。

图1 自适应内联观测器的结构框图Fig.1 Adaptiveinterconnected observer diagram

图2为自适应内联观测器第一个子系统的结构框图，该子系统的输入主要来自整个系统的输入和第二个子系统的输出两个方面。

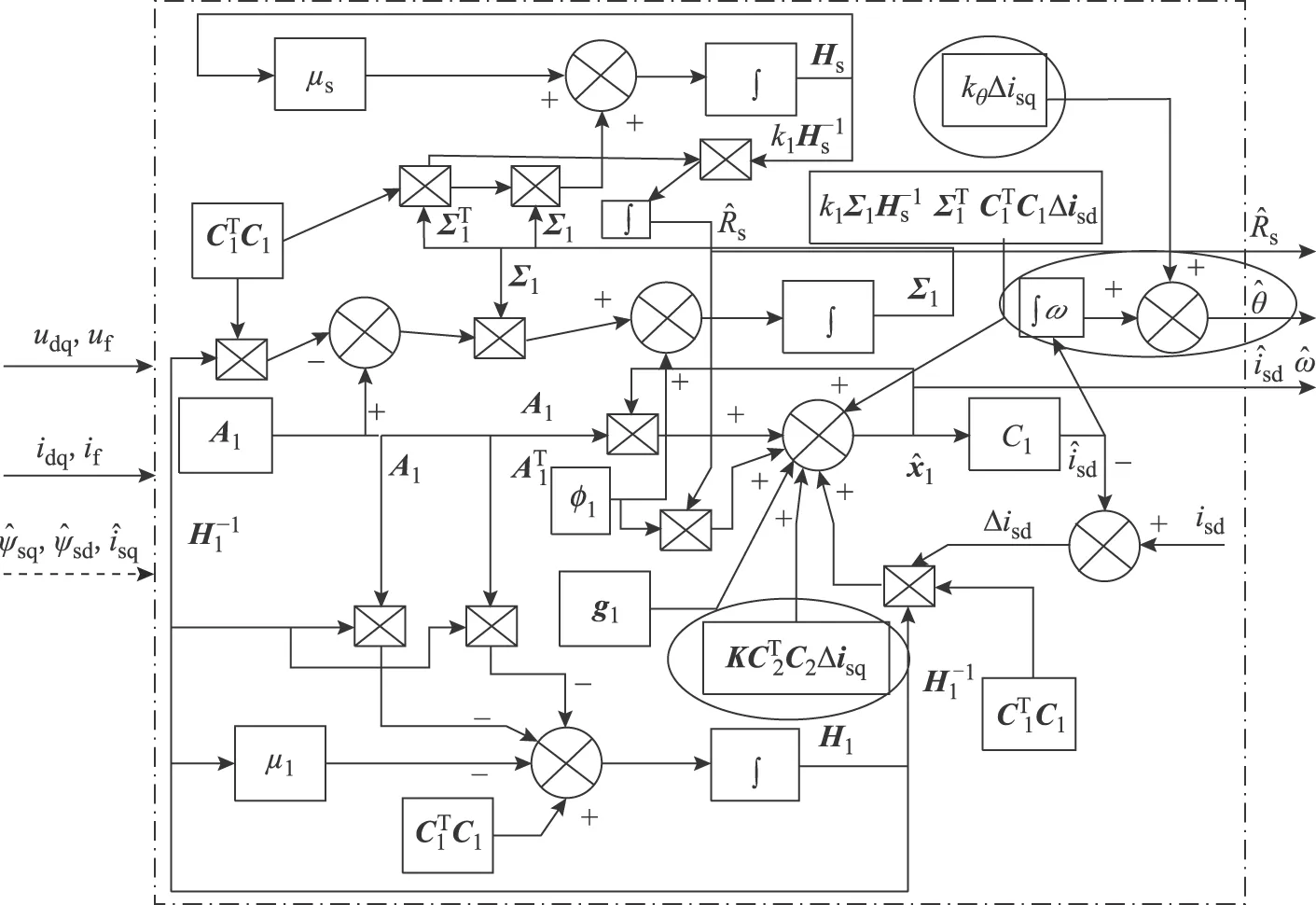
图2 子系统Ω1的结构框图Fig.2 The diagram of subsystem Ω1

由此可知，自适应内联观测器EESM无传感器控制的基本原理是将EESM模型作为参考模型，将所采用的内联观测器作为可调模型。内联观测器由两个子系统观测器组成，其内部相互关联(如电机磁链、定子电阻等)，共同构成可调模型。该方法的输入为定子电压、电流、励磁电压和励磁电流，通过一定的自适应率控制输出得到EESM矢量控制需要的转速、位置角、q轴电感等信息。

该自适应内联观测器的具体实施步骤和参数设定如下：

1)电机本体参数初始化：如电机定子电阻、定子漏感、d轴电感、q轴电感等进行初始化，其初始值一般根据已知电机厂家参数来确定。

2)电机状态类参数初始化：如电机定子dq轴电流、dq轴磁链、速度、负载转矩等。在静态起动情况下，d轴磁链根据ψsd=Lmdif计算得到，其他状态初始值一般都设置为0。

4)根据观测器的设计，反馈增益的选取需根据李雅普诺夫稳定性定理和工程实践经验相结合的方法来确定。k1、k2用于调节系统的收敛速度，一般设置在0到 2之间；kθ是与位置角辨识相关的增益，通常在0到 1之间；λ1、λ2是与速度和转矩相关的增益，电励磁同步电机由于带载能力很强，一般设计的反馈增益较大。最后根据工程实践中得到的电励磁同步电机的状态量和参数的取值范围，应用李雅普诺夫稳定性分析方法推算得到反馈增益μ1、μ2、μs和μL的范围，使得系统稳定。观测器的反馈增益会影响系统的动态性能和稳态性能，需要反复调试以得到最优参数值。

2.2 稳定性分析

考虑到电机的参数具有不确定性，则系统可以写成如下形式

(11)

(12)

式中，带有Δ标志的代表相对应的不确定性项，其具体表现形式为

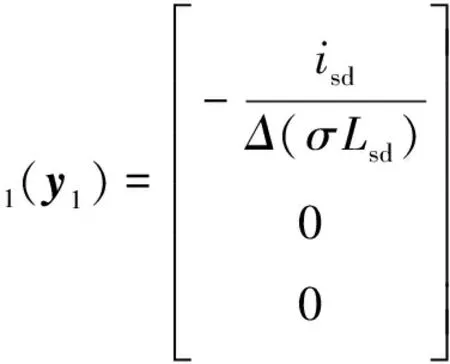
ΔA2(x1) =Δg2(u,y,Rs,x1,x2)

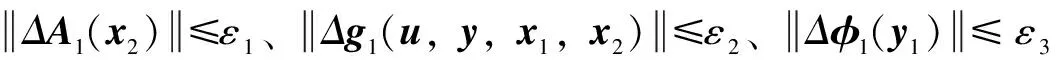
由此，可以定义误差项为

(13)

其中

对式(13)求微分，并根据ћ=ћ1-Σ1ћ3，ћ′=ћ2-Σ2ћ4做变换，得到

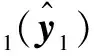
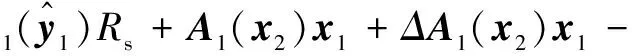
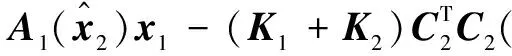
(14)

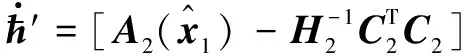
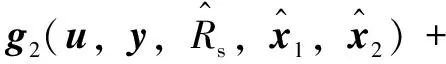
(15)

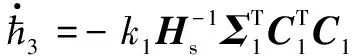
(16)

(17)

(18)

由此，得到以下推论：

若同步电机的扩展模型式(3)～式(5)满足假设①、②的条件，且存在正定的实对称矩阵H1、H2、Hs和HL，满足μ1、μ2、μs和μL均为正常数，则设计的自适应内联观测器式(9)和式(10)能够达到一致渐近稳态。

其具体证明见附录。

图3 矢量控制系统结构Fig.3 Vector control system diagram

3 仿真结果

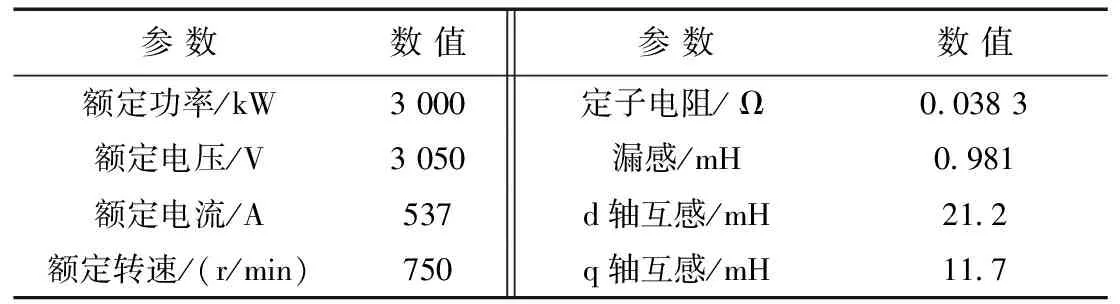
表1 电励磁同步电机的主要参数

1)电动状态下电机的加载及带载加减速运行。

由图4电动状态下的电机波形可看出，电机估计速度与实际转速(图4a)在稳态时辨识误差控制在0.1%左右，动态过程中辨识误差在+5 rad/s～-5 rad/s之间；α相的电压和电流同相位(图4b)，保持高功率因数运行；位置角(图4c)稳态误差小于0.5%；电感的辨识误差(图4d)在0.9%以内。图5为图4在4.4～5.8s时的局部展开波形，更清楚地说明了辨识值能快速准确地跟踪实际值。

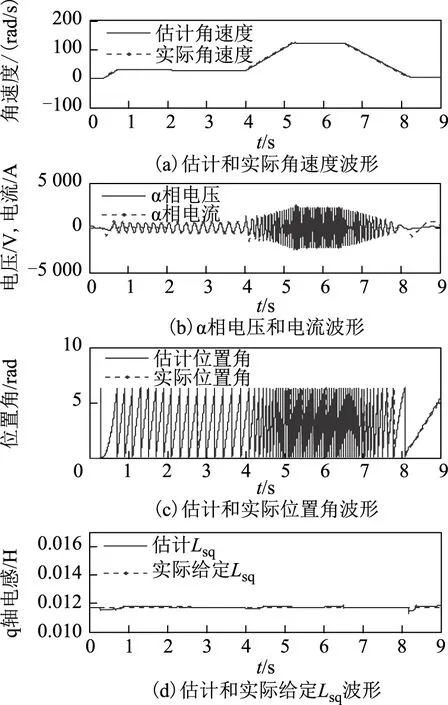
图4 电动状态下电机波形Fig.4 Waveforms in electric state

图5 电动状态下局部展开波形Fig.5 Local expanded waveforms in electric state

2)发电状态下电机的加载及带载加减速运行。

发电状态下，0.3s时给定-30%的额定转速，在2s时加额定转矩，在4s时加速到-80%额定转速。

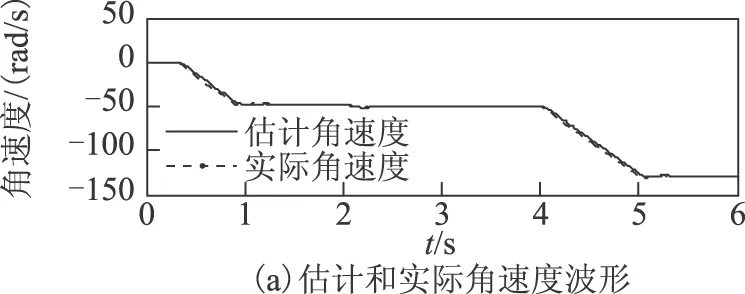
图6 发电状态下电机波形Fig.6 Waveforms in power generation state

4 实验结果

为了进一步验证该方法的有效性，利用对拖系统作为实验平台进行试验，其中电励磁同步电机是被试电机，电机参数见表1，异步电机作为配试电机主要做加载用。两台电机分别由一台三电平变流器拖动，采用二极管中点钳位型变流器，两台变流器采用公共直流母线方式，直流电压为4 840 V，以下分别从电动和发电两种运行工况来测试。

1)电动状态下实验波形。

图7为在20%额定速度加额定转矩时(100 ms以内负载转矩从0加载到额定转矩)α相电流、电压和位

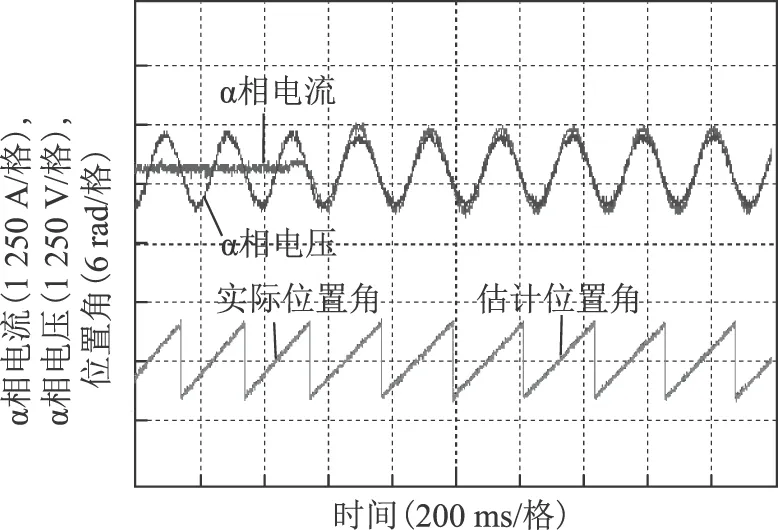
图7 20%额定速度施加额定转矩实验波形Fig.7 Experiment waveforms at 20% rated speed applied rated torque

置角的局部展开波形。由图可看出，未带负载时，电流较小，随着负载的增大，电流快速变大，最后趋于稳定，电压和电流相位差接近于零。实际位置角与估计位置角重叠，辨识快速准确。

图8为在施加额定转矩的条件下，速度由20%额定速度加载到80%额定速度的实验波形。由图可看出，α相电压和电流都将变大，特别是电流在加速瞬间会突然变大，在动态过程中估计位置角仍较为准确。

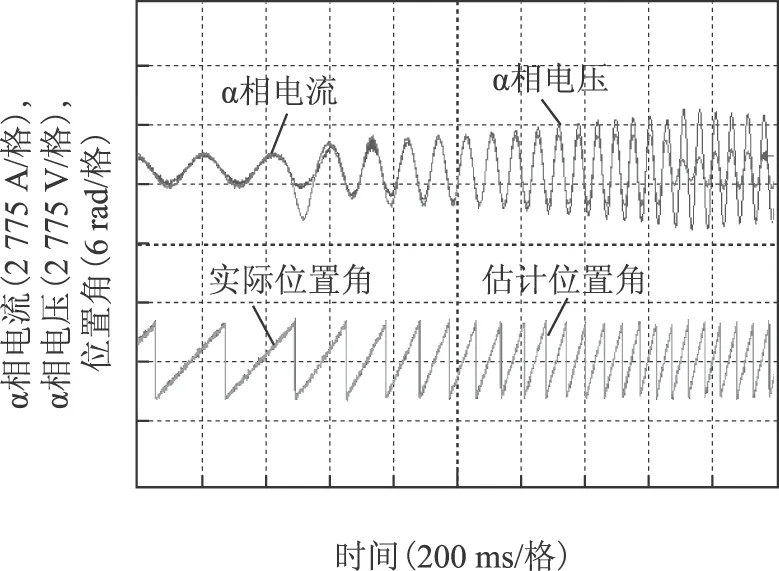
图8 额定转矩下速度由20%加速到80%额定速度的实验波形Fig.8 Experiment waveforms inaccelerate mode from 20% to 80% rated speed with rated torque

2)发电状态下实验波形。

图9为发电状态下，在-30%额定速度加载的实验波形(100 ms以内负载转矩从0加载到额定转矩)。由图可看出，此时α相的电压和电流相角相差180°，位置角估算准确。

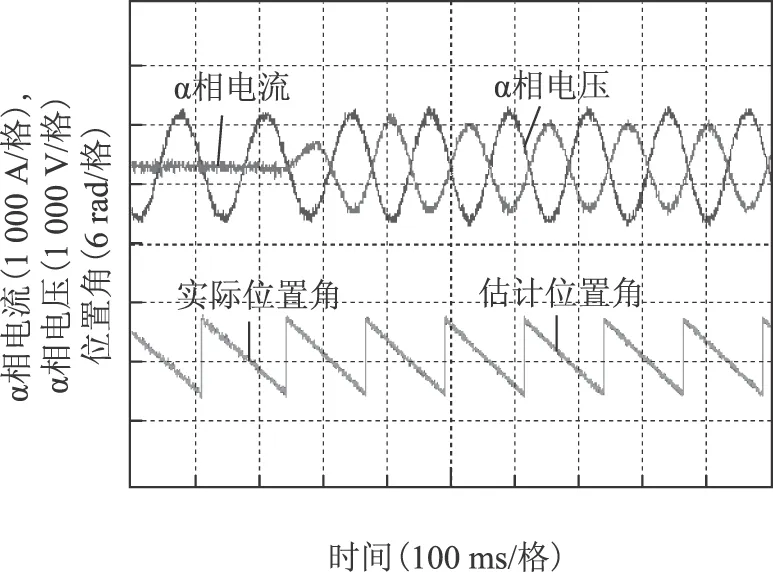
图9 在-30%额定速度加载额定转矩的实验波形Fig.9 Experiment waveforms at -30% rated speed applied ratedtorque

图10为在发电状态下，电机由-30%额定速度减到-80%额定速度的实验波形，实验结果与仿真结果相符合，进一步验证了该方法的有效性。

图10 额定转矩下速度由-30%减到-80%额定速度的实验波形Fig.10 Experiment waveforms in decelerate mode from -30% to -80% rated speed with rated torque

5 结论

本文提出了一种基于自适应内联观测器的电励磁同步电机无位置传感器矢量控制方法，该方法能够同时辨识电机的速度和位置以及电机关键参数q轴电感，仿真和实验证明无论电机运行在电动状态还是发电状态，该方法都能在宽速度范围内保持快速和精确的辨识和跟踪，同时能不断在线修正q轴电感的参数，使电励磁同步电机始终保持在最优运行状态。

附 录

证明：取如下李雅普诺夫函数

(A1)

对其求导，得到

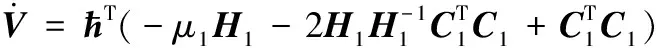
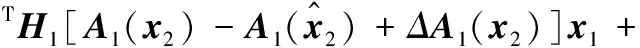
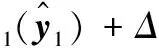
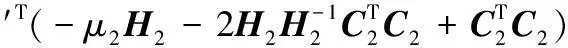
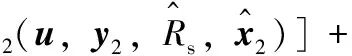
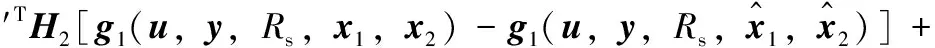
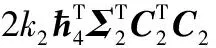
(A2)

根据式(8)，得到

(A3)

将式(A3)带入式(A2)，得到

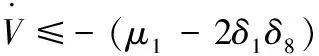
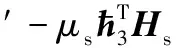
2(δ1δ11δ5+δ1δ7+δ2δ13δ6+δ2δ9-δ1δ16-δ1δ17)‖ћ‖‖ћ′‖+

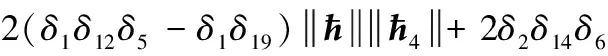
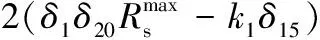
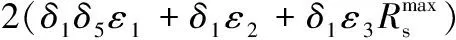
(A4)

将式(A4)写成V1、V2、V3、V4的形式，并利用如下不等式

(A5)

式中，τ1、τ2、τ3、τ4、τ5∈[0,1]，按照文献[14]的处理方法，得

[1] 吴轩钦，谭国俊，何凤有，等.基于有效磁链的电励磁同步电机无速度传感器控制[J].电工技术学报，2016，31(6)：81-90.WuXuanqin，TanGuojun，HeFengyou，etal.Speedsensor-lesscontrolofelectronicallyexcitedsynchronousmotorbasedonactive-flux[J].TransactionsofChinaElectrotechnicalSociety，2016，31(6)：81-90.

[2] 刘洋，史黎明，赵鲁，等.电励磁同步电机惯性储能直流馈电系统新型单位功率因数控制[J].电工技术学报，2016，31(1)：147-154.LiuYang，ShiLiming，ZhaoLu，etal.Anovelunitypowerfactorcontrolofelectricallyexcitedsynchronousmotorinaninertiawheelenergystoragesystem[J].TransactionsofChinaElectrotechnicalSociety，2016，31(1)：147-154.

[3] 李彪，李黎川.基于高性能磁链算法的永磁同步电机无位置传感器控制[J].电工技术学报，2016，31(11)：59-66.LiBiao，LiLichuan.Positionsensorlesscontrolofpermanentmagnetsynchronousmotorbasedonhighperformancefluxestimationalgorithm[J].TransactionsofChinaElectrotechnicalSociety，2016，31(11)：59-66.

[4] 刘海东，周波，郭鸿浩，等.脉振高频信号注入法误差分析[J].电工技术学报，2015，30(6)：38-44.LiuHaidong，ZhouBo，GuoHonghao，etal.Erroranalysisofhighfrequencypulsatingsignalinjectionmethod[J].ElectricDriveAutomation，2015，30(6)：38-44.

[5] 郑泽东，李永东，MauriceFadel，等.采用Kalman滤波器进行信号处理的高频信号注入法在电动机控制中的应用[J].电工技术学报，2010，25(2)：54-59.ZhengZedong，LiYongdong，MauriceFadel，etal.ApplicationofhighfrequencysignalinjectionmethodinmotorcontrolusingKalmanfilterforsignalprocessing[J].TransactionsofChinaElectrotechnicalSociety，2010，25(2)：54-59.

[6]BoseBimal′sK.ModernpowerelectronicsandACdrives[M].Beijing：ChinaMachineryPress，2004.

[7]GendusoF，MiceliR，RandoC，etal.BackEMFsensorless-controlalgorithmforhigh-dynamicperformancePMSM[J].IEEETransactionsonIndustrialElectronics，2010，57(6)：2092-2100.

[8] 胡维昊，王跃，李明烜，等.基于MRAS的多相永磁直驱型风力发电系统无速度传感器控制策略研究[J].电力系统保护与控制，2014，42(23)：118-124.HuWeihao，WangYue，LiMingxuan，etal.Researchonsensorlesscontrolstrategyofdirectdrivemulti-phasePMSGwindpowergenerationsystembasedonMRAS[J].PowerSystemProtectionControl，2014，42(23)：118-124.

[9] 张勇军，孙寅飞，王京.基于单维离散滑模的模型参考自适应转速辨识方法[J].电工技术学报，2012，27(4)：54-58.ZhangYongjun，SunYinfei，WangJing.Aspeedestimationalgorithmbasedonsingle-manifolddiscretetimeslisingmodemodelreferenceadaptivesystem[J].TransactionsofChinaElectrotechnicalSociety，2012，27(4)：54-58.

[10]茅靖峰，吴爱华，吴国庆，等.基于扩张状态观测的永磁直驱风力发电系统MPPT自适应滑模控制[J].电力系统保护与控制，2014，42(18)：59-65.MaoJingfeng，WuAihua，WuGuoqing，etal.AdaptiveslidingmodeMPPTcontrolforPMSG-basedwindenergyconversionsystemsbasedonextendedstateobserver[J].PowerSystemProtectionandControl，2014，42(18)：59-65.

[11]向国菲，佃松宜，蒲明.基于EKF永磁同步电机无传感直接转矩控制研究[J].控制工程，2015，22(3)：369-374.XiangGuofei，DianSongyi，PuMing.EKF-basedpermanentmagnetsynchronousmotordirecttorquesensing[J].ControlEngineering，2015，22(3)：369-374.

[12]谷志锋，朱长青，邵天章，等.全状态EKF估计的最优反演鲁棒励磁控制设计[J].电力系统保护与控制，2013，41(19)：118-125.GuZhifeng，ZhuChangqing，ShaoTianzhang，etal.Designoftheoptimumback-steppingnonlinearrobustexcitationcontrolbasedontheallstateparametersEKFestimate[J].PowerSystemProtectionandControl，2013，41(19)：118-125.

[13]BesanconG，HammouriH.Onobserverdesignforinterconnectedsystems[J].JournalofMathematicalSystems，Estimation，andControl，1998，8(3)：1-25.

[14]TraoreD，DeLeonJ，GlumineauA，etal.Adaptiveinterconnectedobserverforsensorlessinductionmotor[J].InternationalJournalofControl，2009，82(9)：1627-1640.

[15]TraoréD，DeLeonJ，GlumineauA.Adaptiveinterconnectedobserver-basedbacksteppingcontroldesignforsensorlessinductionmotor[J].Automatica，2012，48(4)：682-687.

[16]HamidaMA，GlumineauA，DeLeonJ.Highperformancequasi-continousHOSMcontrollerforsensorlessIPMSMbasedonadaptiveinterconnectedobserver[C]//2012IEEE51stAnnualConferenceonDecisionandControl(CDC)，2012：7107-7112.

[17]HamidaMA，DeLeonJ，GlumineauA，etal.Anadaptiveinterconnectedobserverforsensorlesscontrolofpmsynchronousmotorswithonlineparameteridentification[J].IEEETransactionsonIndustrialElectronics，2013，60(2)：739-748.

[18]JeongI，GuBG，KimJ，etal.Inductanceestimationofelectricallyexcitedsynchronousmotorviapolynomialapproximationsbyleastsquaremethod[J].IEEETransactionsonIndustryApplications，2015，51(2)：1526-1537.

[19]BesanconG，DeLeon-MoralesJ，Huerta-GuevaraO.Onadaptiveobserversforstateaffinesystems[J].InternationalJournalofControl，2006，79(6)：581-591.

(编辑 于玲玲)

Sensorless Control of EESM Based on Adaptive Interconnected Observer

ShangJing1，2NianXiaohong1LiuLi2NanYonghui2

(1.School of Information Science and Engineering Central South University Changsha 410083 China 2.CRRC Zhuzhou Institute Co.Ltd Zhuzhou 412001 China)

In order to solve the problem of rotor angle identification of electrically excited synchronous motor(EESM)，this paper proposed a rotor position identification method based on an adaptive interconnected observer for nonlinear model.Firstly，an expansion model of EESM was established；Secondly，the model was separated into two interconnected subsystems and feedback gain for subsystems was designed respectively.Thus，an adaptive interconnected observer can be obtained.Lastly，Lyapunov stability theorem was used to prove the stability of the proposed method.The method can obtain the speed，position angle and q axis inductance according to the measured voltage and current signals，and the identified information was feedbacked to the control loop to further optimize the control performance.The simulation results show that the method can achieve stable accurate operation on a wide speed range in the electric state and power generation state，and the identification of q-axis inductance value can be quickly and accurately followed the real value.The experimental results further proved the effectiveness of the proposed method.

Interconnected observer，electrically excited synchronous motor(EESM)，sensorless control，stability analysis

国家自然科学基金项目资助(61473314，61403425，61321003)。

2016-01-22 改稿日期2016-06-27

TM921.2

尚 敬 男，1977年生，博士，研究方向为大功率交流电机传动控制。

E-mail：csr2003888@163.com(通信作者)

年晓红 男，1965年生，教授，博士生导师，研究方向为交流技术与传动控制、复杂多体系统控制和优化。

E-mail：xhnian@csu.edu.cn