基于训练序列的MIMO-OFDM同步技术改进

滕孝杰，颜 彪，李 薇，阿孜古丽·艾合拜尔

(扬州大学 信息工程学院，江苏 扬州 225009)

基于训练序列的MIMO-OFDM同步技术改进

滕孝杰，颜 彪，李 薇，阿孜古丽·艾合拜尔

(扬州大学 信息工程学院，江苏 扬州 225009)

从MIMO-OFDM系统的定时同步及频率偏移的问题出发，以Park特殊训练序列结构为基础，提出了一种改进的训练序列结构。该训练序列结构被分为三部分，一、二部分训练符号相同，第三部分重复复制第二部分的后半部分，再分别利用它们的相关性来进行定时同步位置和频率偏移的估值计算。仿真结果表明，该方法使MIMO-OFDM系统的同步性能得到了显著提高。

MIMO-OFDM；训练序列；定时同步；频率偏移

在相同的发射功率和传输带宽下，多输入多输出(MIMO)系统比传统的单输入单输出(SISO)系统的信道容量提高40多倍，同时MIMO系统可以利用多副天线所带来的多条传输路径来获得空间分集增益，从而提高系统的传输性能[1]。正交频分复用(OFDM)技术是一种高效的多载波调制传输技术，它既可以有效地对抗多径传播，也可以使系统带宽的利用率提高。MIMO-OFDM技术是将MIMO与OFDM技术有效结合形成的一种新技术，该技术是在OFDM传输系统中采用阵列天线来实现空间分集，提高信号的传输质量。MIMO-OFDM技术具有频谱利用率高，传输效率高以及传输稳定等优点。但是，MIMO-OFDM系统在高速移动的环境下，容易产生定时偏移和频率偏移，这就使MIMO-OFDM系统对定时同步和频率同步的要求提高，以此来实现数据高效、准确的传输。目前已有大量学者对该同步技术进行了研究分析，有循环前缀同步，导频同步，训练序列同步等[2-6]。本文以Park特殊结构的训练序列为基础，以Zadoff-Chu序列构成训练序列，将训练序列结构分为三部分，第一部分与第二部分的训练序列结构完全相同，第三部分被平均分为两部分，这两部分的训练序列都复制第二部分的后半部分的训练序列，即第三部分的前后两段的训练序列结构完全相同。在算法上，以传统定时同步算法Schmidl&Coc算法(简称SC算法)为基础，将第一、二部分和二、三部分分别进行相关计算，然后再进行求和，最后结合定时判决函数以及频偏公式来获得定时同步和频率偏移的值，并对其进行性能仿真验证及分析。

1 MIMO-OFDM系统的同步算法

1.1 MIMO-OFDM系统模型

假设MIMO-OFDM系统有Nt根发送天线，Nr根接收天线，则其系统模型结构框图如图1所示。

图1 MIMO-OFDM系统模型结构框图

在MIMO-OFDM系统等效模型中，各个发送端的发送天线所发送的OFDM符号可以表示为：

(1)

式中，P表示发送天线的序号；N表示子载波的个数；Sp(k)则表示MIMO-OFDM系统传输的调制符号，可以为BPSK，QPSK或者QAM调制。

在高斯信道下，各个接收端的接收天线所接收的信号可以表示为：

(2)

其中，q表示发送天线的序号；hp,q(l)表示信道的冲激响应；θ表示定时偏移；ω(n)表示频率偏移。

1.2 Zadoff-Chu序列

恒包络零自相关序列(CAZAC序列)具有幅值恒定、理想的相关特性、低峰均比特性等优点，Zadoff-Chu序列在CAZAC序列基础之上提出，同样具有CAZAC序列的优点。由文献[7]知Zadoff-Chu序列{ak}定义为：

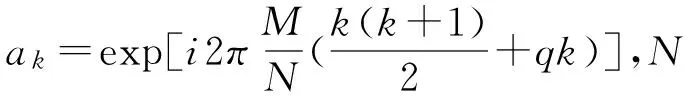
(3)

(4)

M与N是互为质数的整数，q为任意的整数，本文中为了便于计算，q取值为0。

1.3 符号定时同步算法

目前常用的基本符号定时同步算法有三种，SC算法，Minn算法和Park算法，其他的改进结构和算法也几乎都是在这三种基础之上进行的。三种算法训练序列结构图分别如图2。

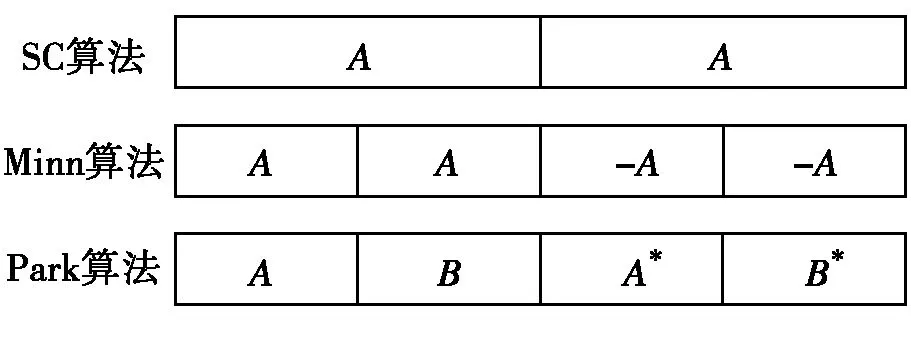
图2 训练序列结构图

其中，字母符号相同，则训练符号相同，负号表示取反，“*”表示共轭，A与B则是呈中心对称。

以SC算法为例，其定时判决函数为[8]：

(5)

上式中

(6)

(7)

而Minn算法和Park算法也都是在此算法基础之上进行改进的，这里不再赘述。

2 改进的同步方法

改进的训练序列结构由三段训练符号组成，第二段重复第一段，第三段的前后两部分分别重复第二段的后半部分，不同天线上的训练序列结构由此循环移位得到。本文设计的序列结构框图如图3所示。

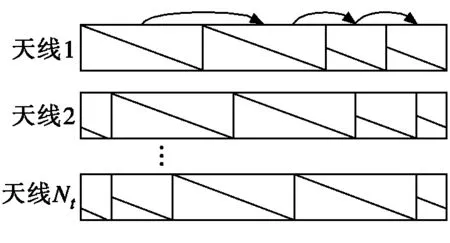
图3 改进训练序列结构图

算法上，传统SC算法由于循环前缀的原因，极易产生定时平台，影响定时同步的准确率；Minn算法和Park算法虽对其进行了改进，使定时点变的相对尖锐，但是计算量也随之增加。本文在算法上仍采用SC算法的定时判决函数，再结合Minn算法和Park算法对其作一定的改进。先对一二部分进行相关运算，再对二三部分进行相关计算，最后结合两次相关计算，进行定时同步及频率偏移的计算。由于第三部分并未完全复制第二部分，其与第二部分的相关性则受到了一定的抑制，使定时点趋于尖锐，从而提高了定时同步准确率。本文定时判决函数如下：

(8)

式中

(9)

(10)

P1(d)=P11(d)+P12(d) .

(11)

(12)

(13)

R1(d)=R11(d)+R12(d) .

(14)

当式(8)的判决函数取得最大值时，即可获得定时符号的起始点d1，再将d1代入频偏公式得出频偏估算ε1。

d1=argmax(M1(d)) .

(15)

(16)

3 仿真分析

在本文仿真中，MIMO-OFDM系统的仿真参数设置为：子载波数目N为256；调制方式为BPSK；循环移位长度为10；系统带宽为20 MHz；载波频率为5 GHz。

误码率及定时同步准确率都可以用来衡量定时同步的性能。图4显示了在收发天线数目为1×1和2×2的情况下误码率随着信噪比变化的曲线走势图。从图中可以看出，无论收发天线数目是在1×1还是2×2的情况下，本文提出的算法在信噪比相同的情况下误码率都要比传统算法低，尤其是在信噪比小于15 dB的情况下。单看本文提出的算法，收发天线数为2×2的误码率要比1×1的误码率低，可见随着天线数目的增加，系统的误码率在降低，同步性能在提高。

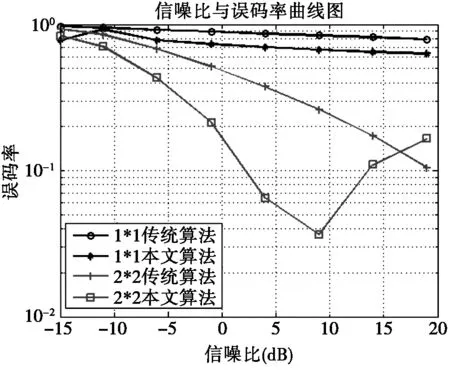
图4 误码率曲线图

图5显示了在收发天线数为2×2的情况下，MIMO-OFDM系统的定时同步准确率随着信噪比变换的曲线走势图。由图可以明显看出本文提出的算法的定时准确率比传统算法的要高，在改善系统的同步性能方面也就更为优越。

4 结束语

本文对MIMO-OFDM系统的定时同步及频率偏移的问题进行了研究分析。对训练序列结构进行改进的同时在算法上也进行了优化。仿真结果表明，本文提出的结构方法与同类方法进行比较，不光降低了训练序列结构的复杂度，还减小了计算量，同时在信噪比相同的情况下，误码率降低，定时准确率提高，MIMO-OFDM系统的同步性能整体也随之得到优化。

[1] 林云，何丰.MIMO技术原理及应用[M].北京：人民邮电出版社，2010:2-3.

[2] Chen B,Zhang Z,Yue H,et al.Reaserch on Synchronization Issues of CP-OFDM Receiver[C]//International Conference on Electronics Information and Emergency Communication.IEEE,2015.

[3] Lin T C,Phoong S M.A New Cyclic-Prefix Based Algorithm for Blind CFO Estimation in OFDM Systems[J].IEEE Transactions on Wireless Communications,2016,15(6):1-1.

[4] Nasraoui L,Atallah L N,Siala M.Synchronization Technique for MIMO-OFDM WLAN Systems with Space Time Diversity[C]//International Wireless Communications and Mobile Computing Conference,2015.

[5] Chen J.An Improved Training Sequence Based Timing Synchronization Algorithm for MIMO-OFDM System[C]//International Conference on Intelligent Systems Design & Engineering Applications.IEEE Computer Society,2014:165-168.

[6] Suparna S A,Sekhar S,Pillai S S.An Efficient Preamble Design for Timing Synchronization in MIMO-OFDM Systems[C]//International Conference on Control,Instrumentation,Communication and Computational Technologies.IEEE,2015:84-88.

[7] Chu D.Polyphase Codes with Good Periodic Correlation Properties (Corresp.)[J].IEEE Transactions on Information Theory,1972,18(4):531-532.

[8] Schmidl T M,Cox D C.Robust Frequency and Timing Synchronization for OFDM[J].IEEE Transactions on Communications,1998,45(12):1613-1621.

Improvement of MIMO-OFDM Synchronization Technology Based on Training Sequence

Teng Xiaojie, Yan Biao, Li Wei, Arzigul Akbar

(CollegeofInformationEngineering,YangzhouUniversity,YangzhouJiangsu225009,China)

Starting from the problem of timing synchronization and frequency offset of MIMO-OFDM system, an improved training sequence structure is proposed based on Park special training sequence structure. The training sequence structure is divided into three parts-the first and the second parts of the training symbol are the same and the latter part of the second part is copied to the third part repeatedly. Then the timing synchronization position and frequency offset is calculated by using their correlation. The simulation results show that the synchronization performance of the MIMO-OFDM system is improved remarkably.

OFDM-MIMO; training sequence; timing synchronization; frequency offset

2017-01-07

滕孝杰(1995- )，男，江苏宿迁人，大学本科，研究方向为无线通信。

1674- 4578(2017)02- 0052- 04

TN929.53

A